螢火蟲算法優化的卷積網絡在圖像顯著性檢測中的應用*

孫永盛 劉 鎮

（江蘇科技大學計算機學院 鎮江 212000）

1 引言

隨著計算機計算能力的提升與人工智能的發展，利用計算機模擬人眼的視覺注意機制，已成為計算機視覺領域重要的研究方向之一。圖像的顯著性檢測是指通過建立圖像顯著性檢測模型，準確快速地檢測出圖像中的人眼注視區域。完整的圖像顯著性檢測模型需要充分模擬視覺注意機制，然而在實際運用中，由于計算方法和建模方法的限制，檢測出的圖像顯著性區域與實際的人眼注視區域具有一定的差距，檢測的準確度有待進一步提高，模型的檢測速度經常受到嚴重的影響。

卷積神經網絡是機器學習中廣泛應用于圖像處理領域的一種算法，但標準神經網絡預測響應時存在的泛化能力差、收斂慢、網絡預測精度不高等缺陷［1］。據此，本文基于混沌策略優化的螢火蟲算法予以改進，優化神經網絡初始權值和閾值以提高網絡預測性能和精度。結合圖像顯著性檢測的具體應用建立相應的檢測模型，該模型在檢測準確度和檢測速度方面均有顯著的提高，能夠準確快速地檢測出圖像的顯著性區域，并且具有廣泛的適用性。

2 卷積網絡的圖像顯著性檢測

卷積神經網絡模型是機器學習中應用于圖像處理領域中的一種經典模型。它由特征提取層與特征映射層組成。網絡層由卷積層和下采樣層交替形成。卷積層和下采樣層之后，是全連接層輸出［2］。卷積神經網絡結構圖如圖1所示，若輸入圖像大小為n×n，經過卷積層m個s×s的卷積核后，輸出m 個(n-s+1)×(n-s+1)大 小 的 圖 像，經 過 下采樣層后輸出m個(n-s+1)/2×(n-s+1)/2的圖像，依次再經過卷積層和下采樣層。

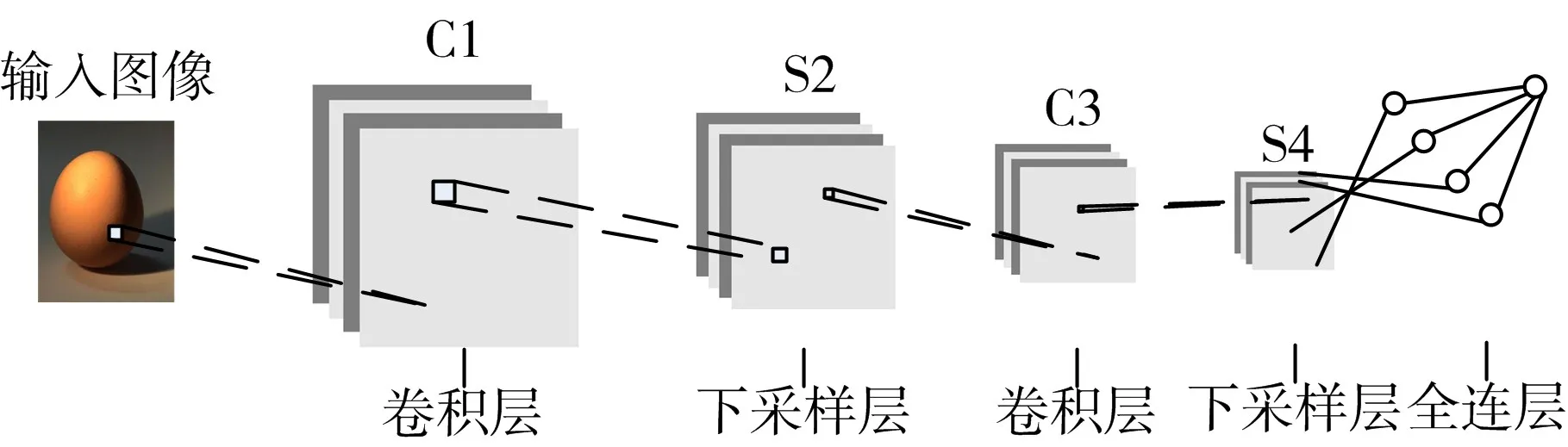
圖1 卷積神經網絡結構圖

圖1中C代表卷積層，S代表下采樣層。卷積層用來進行特征提取，提高模型的魯棒性，公式如下：

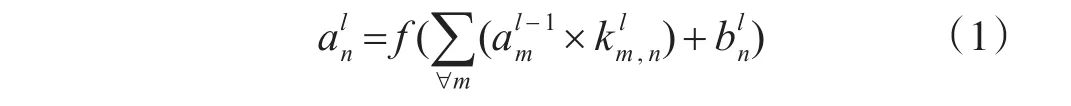
其中表示當前層所卷積出來的特征圖；同樣地，則表示前一層傳遞過來的下采樣層的特征圖；表示從上一層第m個特征圖到當前層第n個特征圖的卷積核；f(x)=1/[1+exp(-x)]為激活函數。代表神經元偏置，是卷積核與上一層特征圖譜卷積和的響應，采用不同的卷積和則可以提取不同的特征［3］。下采樣層是對特征進行映射，減少了特征的分辨率，節省了計算時間，增加量了模型的效率，下采樣層中的節點輸出可以表示為

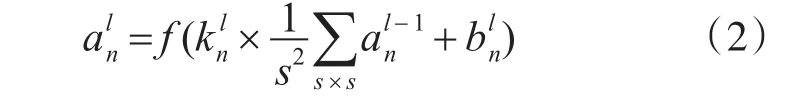
其中表示下采樣層中采樣模板的權值，s×s表示采樣模板的尺寸。最后網絡形成一個全連接層輸出的最后結果，輸出公式如下：

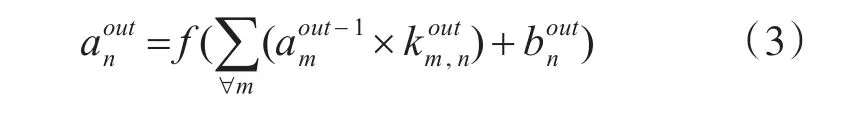
3 標準螢火蟲算法

螢火蟲優化算法（Firefly Algorithm）是一種新型仿生智能優化算法，該算法的仿生原理為：螢火蟲個體總是朝最近、最亮的個體移動，未找到最近最亮個體的螢火蟲規定其在原位置基礎上進行無指導方向的運動；螢火蟲之間的相對吸引力決定了個體的移動距離，越亮的個體其對周圍螢火蟲的吸引力越大，同時對越遠螢火蟲的吸引力越小［4］。

對于待優化問題，其對應的優化函數在定義域中的取值可以作為判斷螢火蟲亮度高低的標準，螢火蟲的位置對應優化函數在定義域中的解。亮度越高的螢火蟲所對應的目標函數值越優，隨著種群不斷進化，整個種群不斷接近最亮的個體，最終獲得優化函數的最優解即對應最亮個體位置［5］。

在螢火蟲優化算法中，個體i到j的距離表示為rij，一般采用歐氏距離［6］，即：

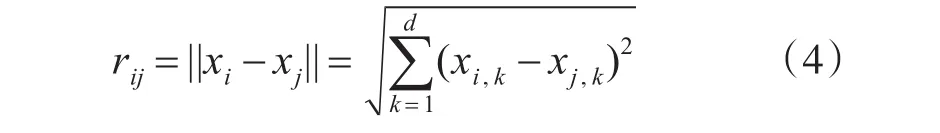
其中d代表搜索空間的維度。

由定義螢火蟲個體i對j的吸引力和其對j的相對亮度成正比，可得螢火蟲i對螢火蟲j的吸引力公式表示為

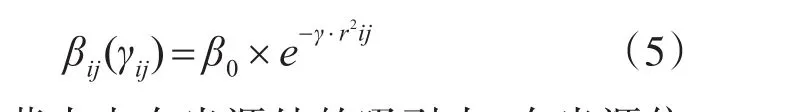
式中，β0表示螢火蟲在光源處的吸引力，在光源位置rij=0，此時螢火蟲具有的吸引力最大，通常取β0=1，γ為光吸收系數，該參數的取值影響螢火蟲優化算法的搜索速度和最終尋優質量［7］。

螢火蟲i相對螢火蟲j的熒光亮度公式為

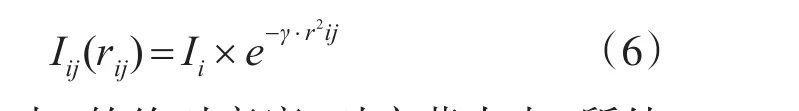
式中，Ii是螢火蟲i的絕對亮度，對應螢火蟲i所處位置的目標函數值：γ表示光吸收系數，從光學角度描述了亮度在傳播過程中會被介質吸收，同時由于距離增加而不斷變暗，一般情況下對γ取常亮［8］。

螢火蟲j被螢火蟲i吸引，j向i移動來更新原來位置，j位置更新公式為

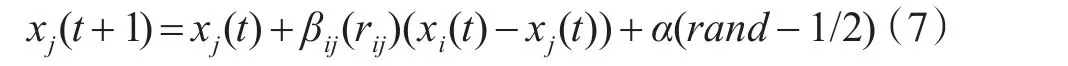
式中，t為算法的迭代次數，xj(t+1)代表螢火蟲j在第t+1次迭代的位置；βij表示個體i對j的吸引力：α為常數，取α∈[0，1]；rand代表隨機數，在[0，1]上服從均勻分布。

4 基于混沌化策略的種群初始化

混沌現象是一種普遍存在于自然界中的一種復雜隨機現象，它具有隨機、遍歷、規律、敏感等特性。從表面上看，混沌運動與隨機運動很相似，但是兩者存在本質的區別。混沌運動是由于確定性的物理規律所形成的，是可以短期預測的［9］。而隨機特性是由內在特性的外部噪聲所產生的。混沌優化就是通過隨機、遍歷和初始值敏感等這些混沌運動所具有的特點來對隨機算法的性能進行改進。

在多種混沌序列的模型中，可知在混沌空間相同的條件下，由邏輯自映射函數生成的序列比logistics映射更具有遍歷性［10］。采用邏輯自映射函數生成混沌序列，如式（8）所示：

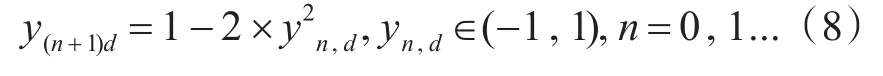
其中，為避免混沌序列出現全為1或0.5的情況，所以初始值不能取0和0.5，d表示D維搜索空間的第d維。

初始化混沌種群的過程［11］描述如下：

1）對于D維空間的M個螢火蟲個體，根據邏輯自映射函數的性質，首先初始化混沌變量，在(-1，1)區間隨機產生初始變量。

2）按照式（8）迭代，將邏輯自映射生成的MaxGen×D-1個混沌變量，與初始混沌變量一起對應全部MaxGen×D個螢火蟲個體。

3）講產生的混沌變量序列按變換到目標函數的搜索空間，生成螢火蟲初始種群的M個個體，公式如下：

式中，Lb和Ub分別表示搜索空間第d維的下限和上限，yn，d是根據式（9）產生的第i個螢火蟲對應的第d維混沌變量，xi，d為第i個螢火蟲在搜索空間中第d維的坐標值。

傳統螢火蟲算法和基于混沌優化策略的種群初始化效果分別如圖2所示。

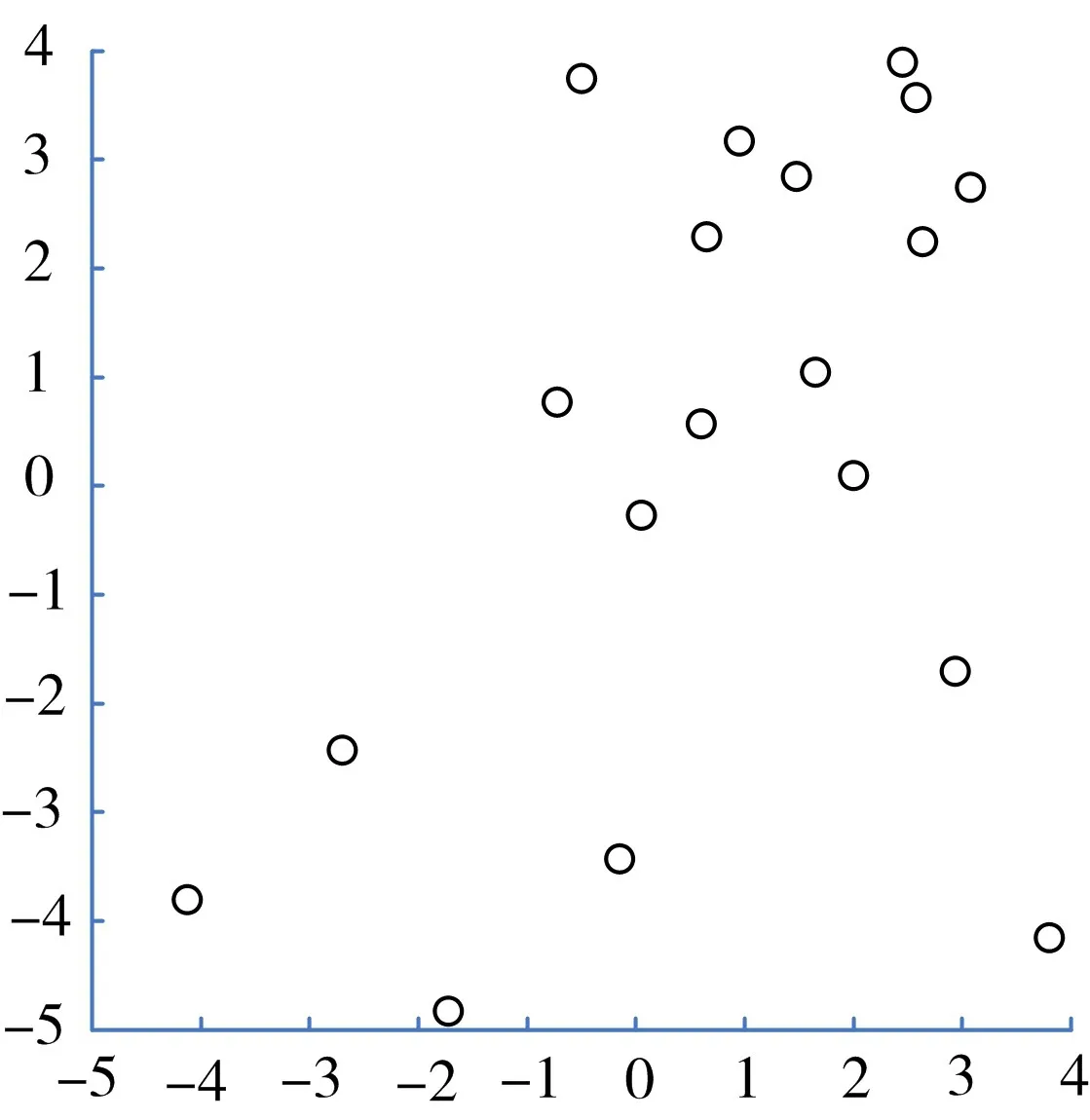
圖2 傳統螢火蟲算法的種群初始化效果圖

從圖2和圖3的初始化種群分布對比可以看出，采用混沌優化策略的初始化種群，種群分布的均勻性要明顯優于采用隨機策略的初始化種群。

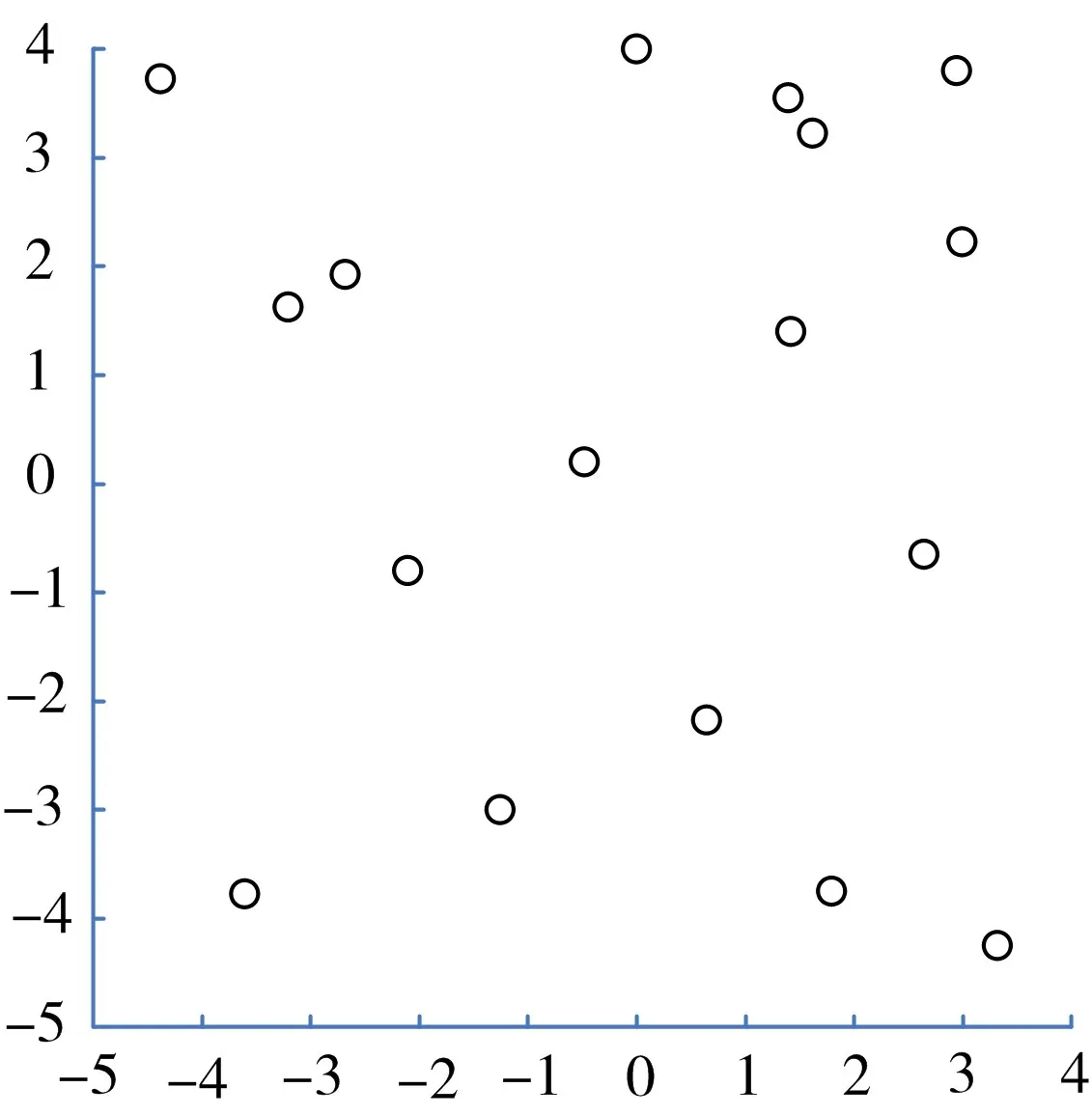
圖3 基于混沌優化策略的和群初始化效果圖

5 基于螢火蟲算法優化的神經網絡

神經網絡結構通常包含輸入層、隱含層和輸出層。輸入、輸出層節點數由訓練樣本的輸入、輸出維數確定［12］。隱含層的節點數根據經驗公式選定。

各層之間的傳遞函數為Sigmiod函數，隱含層第j個節點的輸出：

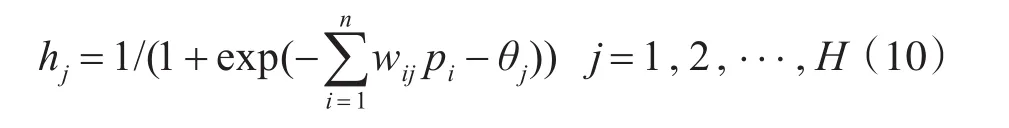
式中wij為輸入層第i個節點到隱含層第j個節點的連接權值；θj為隱含層第j個節點的閾值；pi為隱含層第i個輸入。將隱含層輸出hj進一步向后傳遞，相應得到輸出層第k個節點的輸出［13］：

式中：wˉjk為隱含層第j個節點和輸出層第k個節點之間的連接權值；θˉ為輸出層第k個節點的閾值［14］。

螢火蟲神經網絡訓練時，每個螢火蟲個體xi代表神經網絡各層的連接權值wij、wˉjk和閾值θj、θˉk，個體編碼采用實數矢量形式［15］，則編碼長度（即需要優化的變量總數）由各層節點數N，H和O決定。

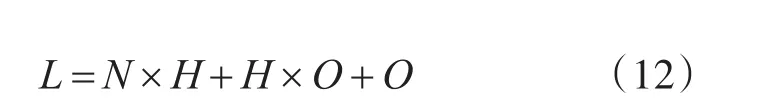
訓練時，神經網絡的訓練精度由誤差RMSE來衡量：

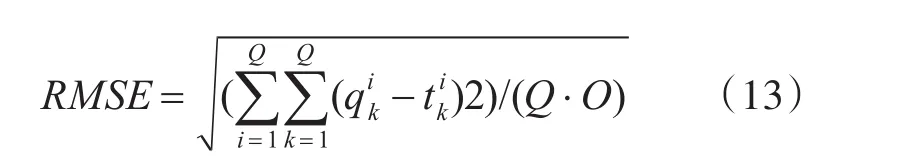
式中：Q為訓練樣本數；為第i個訓練樣本在輸出層第k個節點的期望輸出。

螢火蟲神經網絡訓練過程中，螢火蟲每一個個體代表一個神經網絡，神經網絡的性能用訓練誤差來表示，螢火蟲個體的適應度值可以直接取為該個體代表的網絡訓練迭代終止時的誤差值［16］。

算法流程如圖4所示。

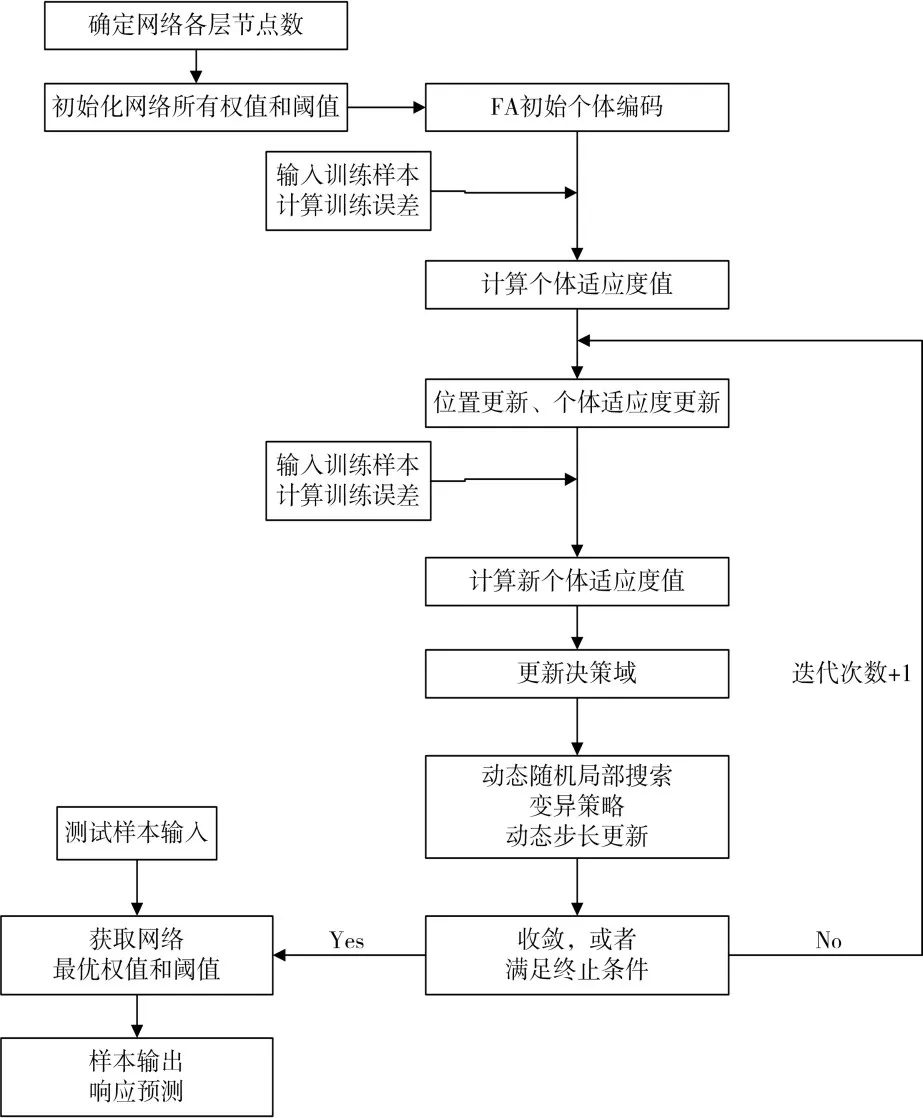
圖4 算法流程圖

6 實驗分析

6.1 實驗條件及評價指標

本文在MSAR圖像數據庫上進行實驗。該圖像數據庫包含動物、植物、人等多種圖像，是顯著性檢測的常用數據庫［17］。本文中的實驗環境為Matlab r2014b，CNN網絡采用五層經典結構。

為了體現顯著性檢測效果，本文采用F-Measure來評價它能夠同時考慮到檢測的準確率和完全率［18］。計算公式如下：

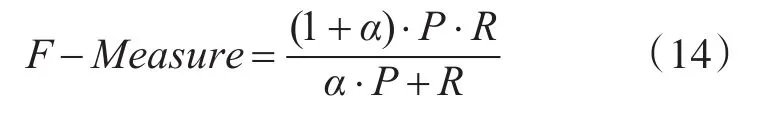
其中，P代表示檢測的準確率；R表示檢測的完全率；α用來衡量F-Measure值是側重于檢測的準確率還是完全率，本文取α為0.3，表示側重于檢測的準確率［19］。

6.2 結果分析

將MSAR圖像數據庫中的圖片分別在AC、FT、SF、SR四種經典的顯著性檢測算法［20］上運行，并與本文算法運行結果、標準GT集對比，結果如圖5所示。

由圖6的實驗數據結果可以看出本文算法的P，R，F-Measure值均高于其它四種算法，證明本文提出的顯著性檢測算法有一定的合理性和優勢。

圖5 對比結果

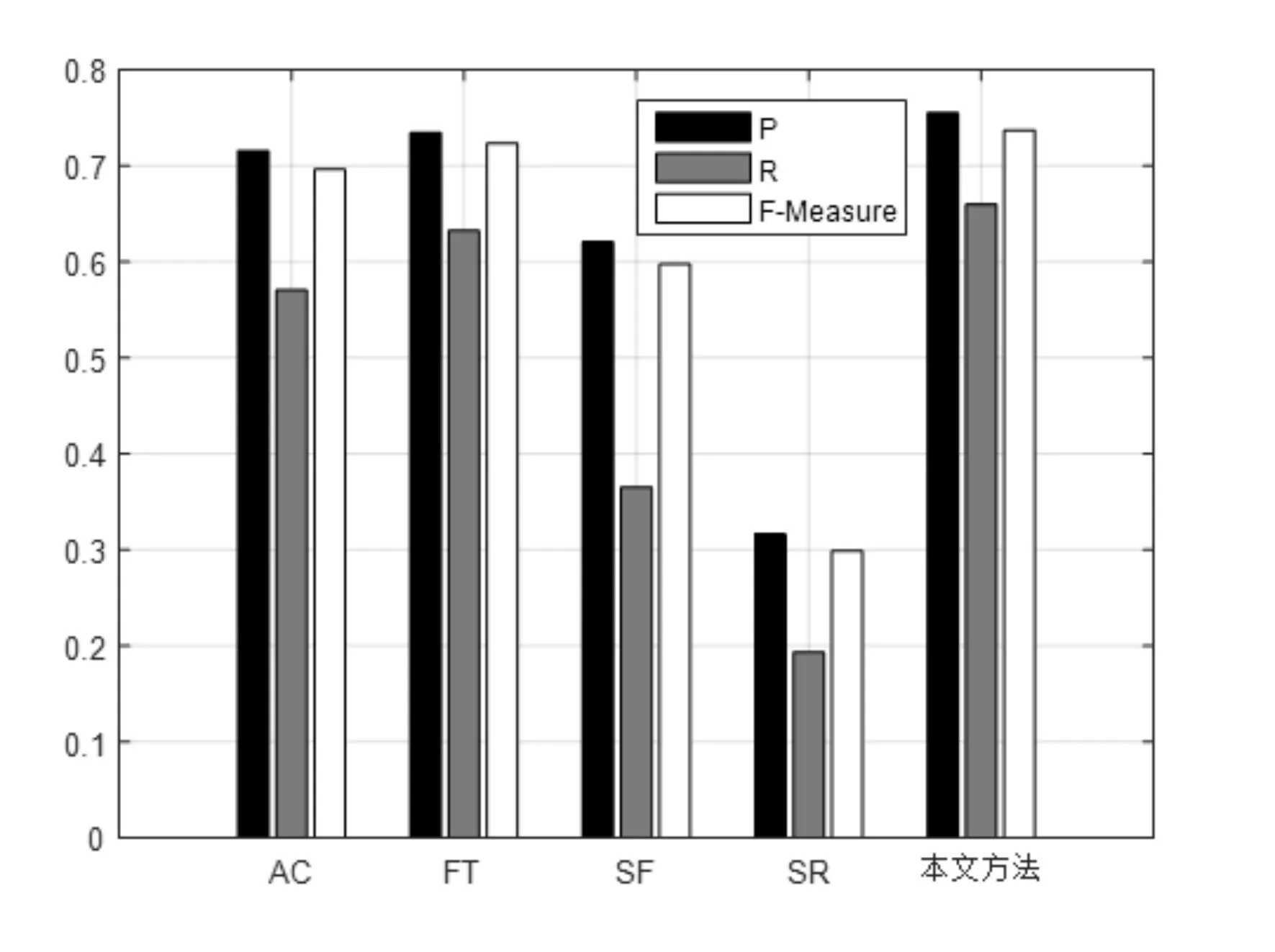
圖6 實驗數據結果

7 結語

本文將混沌序列用于螢火蟲算法的種群初始化，提高了螢火蟲算法初始種群分布的均勻性。構建了螢火蟲算法優化的神經網絡預測模型，優化了神經網絡初始權值和閾值，提高了預測性能和精度。該模型不依賴于目標的形狀、環境和場景的變化，具有較好的魯棒性。利用卷積神經網絡有效地提取顯著性特征，經過特征融合進行顯著性檢測。結果顯示，在主觀觀測和客觀計算結果上顯著性效果均有一定的提高，顯著性結果圖片在清晰度和準確度上也有一定的提高。但對比方法和本文方法都停留在單目標無法很好地處理多目標顯著性的檢測，后續將對多目標的顯著性檢測進行研究。