一種圖像小波去噪的改進閾值函數*

黎彪 刁燕 羅華 徐明

（四川大學機械工程學院 成都 610065）

1 引言

數字圖像是由光線通過鏡頭折射到傳感器上產生模擬信號，再將模擬信號轉換成數字信號，數字信號傳輸回主機設備上得到［1］。在這個過程中，惡劣環境、不佳光線和數據轉換傳輸時丟失部分等，都會產生噪聲，對獲得的圖像質量造成嚴重影響。因此，圖像去噪是圖像預處理的一個重要部分［2～4］。

一直以來，研究人員提出了許多去噪方法。頻域去噪因其將圖像變換到頻域，處理后再逆變換回空域，可以在很大程度上保留原始圖像的細節而備受關注。常見的頻域變換方法有傅里葉變換和小波變換［5］。相比傅里葉變換，小波變換不僅保留圖像的頻率信息，還保留了圖像的空間信息，故近十年來成為圖像處理的重要工具［6～7］。最早的小波閾值去噪方法是由斯坦福大學的D.L.Donoho提出，使用硬閾值和軟閾值函數［8］。但硬閾值函數不連續，會導致去噪后圖像出現振鈴、偽吉布斯現象；軟閾閾值連續卻在較大系數上有恒定偏差，會導致去噪后圖像出現嚴重失真［9］。一些典型的改進閾值函數［10～12］在這兩個問題上有所改善，卻仍有不足。基于小波去噪原理和對傳統閾值函數的分析，本文提出一種改進的閾值函數，其在實數域內連續可導，更加光滑，在較大小波系數上保持一致，減少失真。仿真實驗驗證了改進閾值函數的去噪有效性。

2 小波閾值去噪方法

2.1 去噪原理

假設觀測到含噪聲的圖像信號：

其中：s為原始圖像信號，在某些小波基下可以稀疏表示；噪聲n服從某一分布；N為信號長度。

小波變換是線性變換，因此小波變換：

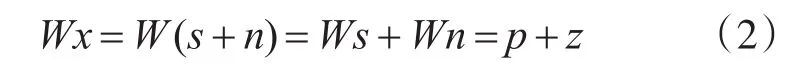
其中：p為原始信號的小波級數，大部分系數是等于零或接近零；z為噪聲的小波級數。在和的小波級數系數中，幅值較大的小波系數主要來自原始圖像信號，幅值較小的小波系數主要來自噪聲［13～14］。所以選取合適的閾值函數，將幅值較大的小波系數輕微減小，將幅值較小的小波系數盡量置零，得到新的小波系數，小波逆變換后就可得到去噪圖像。

2.2 經典閾值函數

硬閾值函數和軟閾值函數在小波去噪中應用最廣。設是觀測圖像的小波變換系數，是值為水平方向H、豎直方向V或對角方向D的上標，j是小波分解層數；是某閾值；是閾值函數得到系數。硬閾值函數：

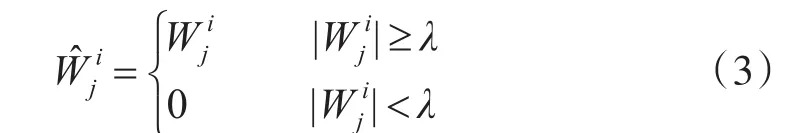
在λ處不連續，會導致小波逆變換后的圖像出現振鈴、偽吉布斯現象。軟閾值函數：

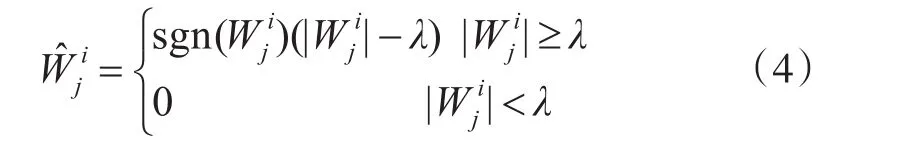
在λ處連續，但大于λ的小波系數都有恒定偏差，包括原始圖像信號的小波系數，使小波逆變換的重構圖像失真。當數如圖1所示，橫坐標是觀測到的含噪圖像小波系數，縱坐標是閾值函數變換后的修改小波系數。

針對硬軟閾值函數的問題，國內外提出了一些改進閾值函數，典型的包括折中閾值函數、雙變量閾值函數和指數閾值函數等。折中閾值函數［10］：

其中：α∈[0，1]。α可以調整軟閾值方法的偏差，但隨著增大，偏差會越來越大；且函數在λ處不連續，會導致圖像失真。當λ=4，α=0.5時，函數如圖2所示。雙變量閾值函數［11］：

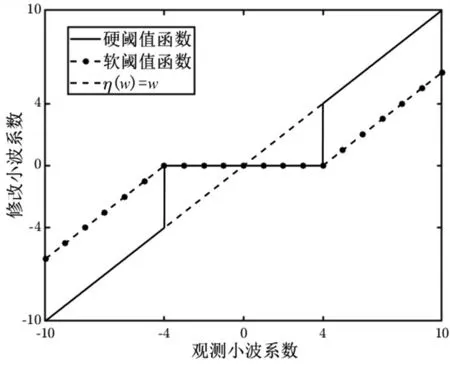
圖1 硬軟閾值函數

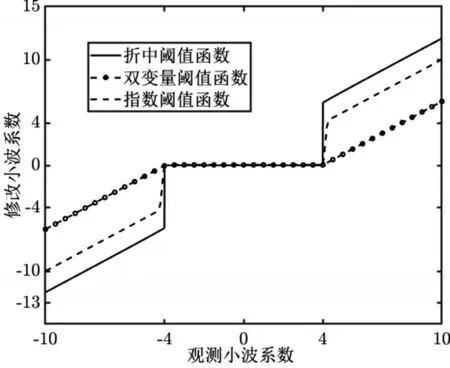
圖2 一些改進閾值函數

指數閾值函數［12］：

3 改進小波閾值函數

3.1 改進的閾值函數

為了克服以上方法的缺點，本文在上述去噪函數的基礎上，提出一種改進函數：

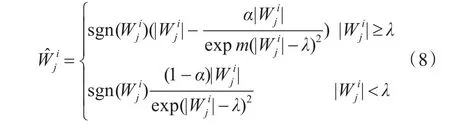
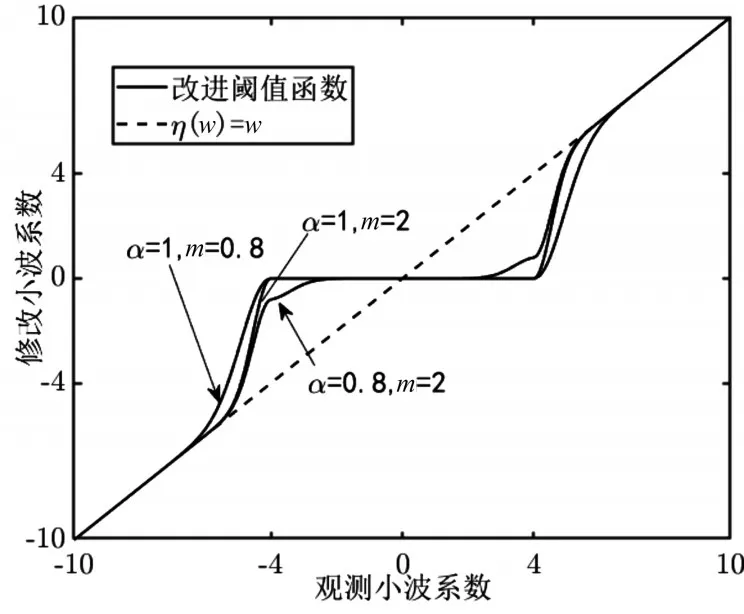
圖3 提出的改進閾值函數

3.2 改進的閾值選取

閾值函數中λ的取值對最后去噪效果有著重要影響，λ應該能夠最大程度上分離噪聲的小波系數和原始圖像信號的小波系數。通用閾值是最常用的取值方法，公式為，σ為噪聲標準差，N為信號長度。隨著小波分解層數增加，噪聲所在的小波系數區域應該逐漸減小，在較高層次分解的小波系數大部分都是來自原始圖像信號。為了更好分離噪聲和原始圖像信號，需要在分解層數增加時減小閾值λ。本文改進的閾值選取表達式為

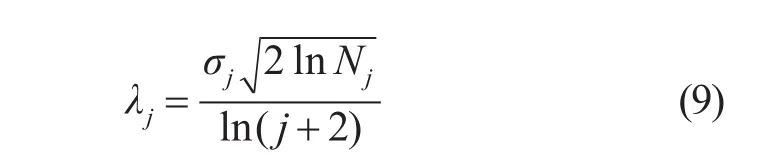
4 實驗對比分析

為了說明改進閾值函數在圖像小波去噪時的有效性，本文使用Matlab2018軟件進行仿真驗證。測試圖像為標準測試圖像［15］中的Baboon圖像、Camera圖像和Peppers圖像。Baboon圖像具有高頻細節，Camera圖像和Peppers圖像具有低頻細節。給原始標準圖像添加密度為0.05的椒鹽噪聲和標準差為35的高斯白噪聲，作為觀測到的含噪圖像。對含噪圖像選擇小波基和分解層數進行小波分解，閾值函數變換后進行小波逆變換得到去噪圖像。本文采用去噪效果較好的db4小波基，分解層數為3層。提出的改進閾值函數的參數設為α=0.9，m=2。去噪結果如圖4～5所示。

圖4 Baboon圖像去噪結果

圖5 Camera圖像去噪結果

從實驗圖像中可以看出：改進閾值函數的去噪效果視覺上更好。為了進一步比較去噪效果，本文使用均方根誤差（RMSE）、信噪比（SNR）和峰值信噪比（PSNR）作為評價標準，表達式：

其中：s為原始標準圖像，s^為去噪圖像，N為總像素數。RMSE越小，SNR越大，PSNR越大，則去噪效果越好。去噪結果如表所示。

圖6 Peppers圖像去噪結果

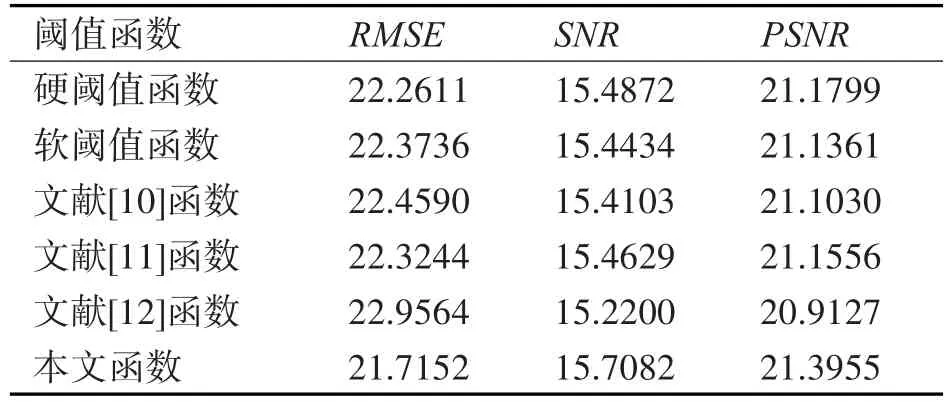
表1 Baboon圖像去噪結果評價

表2 Camera圖像去噪結果評價

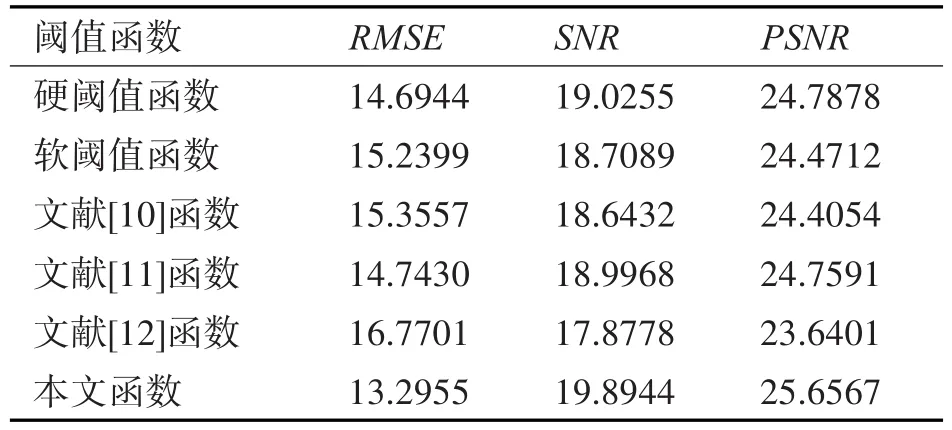
表3 Peppers圖像去噪結果評價

5 結語

根據小波去噪原理，分析小波去噪的傳統閾值函數和幾種典型閾值函數后，提出一種改進的在閾值處可導的閾值函數。從仿真實驗結果中可知，在低頻和高頻細節圖像中，改進閾值函數都獲得更好的去噪效果。改進閾值函數在實數域內連續可導，有助于自適應閾值選取研究，有助于小波去噪在圖像去噪中的發展和應用。