如何在初中數(shù)學課堂教學中滲透數(shù)學思想方法

徐慶梅

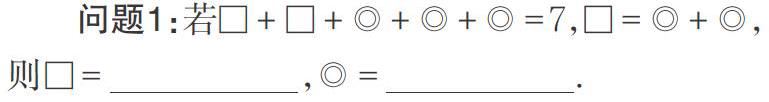
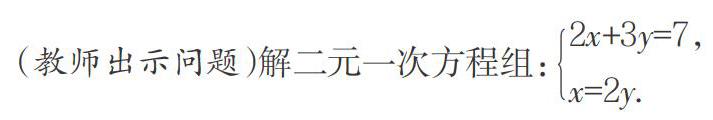
美國教育心理學家布魯納指出：“領會基本數(shù)學思想方法是通向遷移大道的‘光明之路.”《數(shù)學課程標準（2011年版）》指出：“通過義務教育階段的數(shù)學學習，學生能獲得適應社會生活和進一步發(fā)展所需的數(shù)學基礎知識、基本技能、基本思想、基本活動經(jīng)驗，學會獨立思考，體會數(shù)學的基本思想和思維方式.”由此可見，在數(shù)學課堂教學中滲透數(shù)學思想方法十分重要.下面，筆者結(jié)合兩個教學案例，分析和探討一下如何在數(shù)學課堂教學中滲透數(shù)學思想方法，培養(yǎng)學生的數(shù)學思維能力.

一、以解決問題為中心，滲透類比、遷移和轉(zhuǎn)化的數(shù)學思想

教師要改變“教教材”的思維定式，根據(jù)學生的實際情況大膽、創(chuàng)新地“活用教材”，注重數(shù)學思想方法的滲透.在課堂教學中，教師可以適時拋出問題來吸引學生對教學內(nèi)容的注意力，通過引導學生不斷地解決問題幫助學生建立起學習數(shù)學的信心，并以此提升學生對學習數(shù)學的興趣.例如，在教學人教版七年級下冊“利用代入消元法解方程組”時，筆者根據(jù)學生的生活實際，巧妙地更改了教學情境，由玩游戲切入，對例題進行了靈活處理，效果甚好.

教師一拋出上述問題，學生都很激動，都舉起了手，準備回答.這時，教師把機會給了平時從不敢舉手的同學，他們基本上都回答對了.此時，老師適時進行表揚，可以增強學生學習數(shù)學的興趣和信心.

教師：這個游戲，大家都玩得很好.那么，如果把解決這個游戲的思路運用到下面這個問題中，相信大家一定也能玩得很好！

小組探討這個方程組和上面的游戲有什么異同？讓小組代表發(fā)言，老師和其他同學給總結(jié)得好的發(fā)言人鼓掌.當學生通過類比找出異同時，教師追問，能不能用玩這個游戲的方法來解這個方程組呢？給學生足夠時間進行思考，讓學生來講解這個方程組的思路，再讓學生嘗試解這個方程組.解完之后，教師追問，你們能不能總結(jié)一下方法呢？由學生回答后，教師再進行簡短的總結(jié)，強調(diào)并板書本題的書寫格式.在本節(jié)課中，教師不是教具體的解題方法，而是從游戲切入，讓同學們在歡聲笑語和人人參與中解決了問題，總結(jié)出了方法.在老師的引導下，數(shù)學課變得有趣了，學生學起來也更輕松了.這個學習過程滲透了“類比”“遷移”“轉(zhuǎn)化”的數(shù)學思想方法，讓學生釋放出了巨大的學習潛能.

二、引導學生進行深度探究，滲透直觀、對應和模型思想

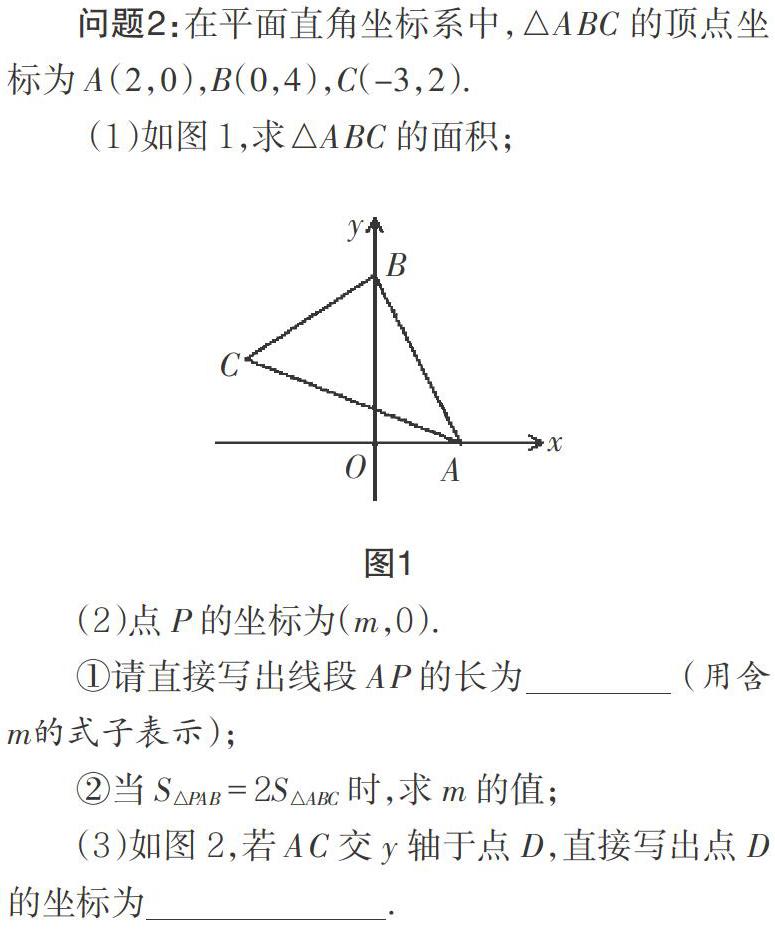
如何實現(xiàn)教科書的育人功能，這需要教師對教科書進行深度加工，用好教材.例如，在復習平面直角坐標系這一章時，教師可以給出下面這樣一道綜合題.

讓學生嘗試解決問題（1）時，學生找不到△ABC的底和高.在他們遇到困難時，教師可以適時點撥：當不能直接求△ABC的面積時，我們是否可以間接求呢？通過解決這一問題，學生體驗到了不能直接求△ABC的面積，但可以通過作輔助線，利用轉(zhuǎn)化的思想進行求解的過程.學生在解決這個問題的過程中積累的感性經(jīng)驗和思考經(jīng)驗，可以為后面的探究打好知識和方法上的基礎.

對于問題（2）的第①問求AP的長，教師可以讓學生自己完成后核對答案，并針對出現(xiàn)的兩種或三種答案，讓學生思考哪種正確，讓學生在回答問題的過程中體悟分類討論思想.接著，教師進行少而精的總結(jié)，并在此基礎上深度探究問題②.在解決這個問題的過程中，學生鞏固了知點求面積的方法，利用分類思想，借助方程求出了m的值，深入探究了方程是用來表示等量關系的模型思想.

對于問題（3），待學生分析思考后，教師讓學生說出他們獲得了什么信息？學生能判斷出點D在y軸上.教師追問：y軸上的點的坐標有什么特點？你們知不知道點的坐標怎么求？小組討論后，學生回答，我們可以把要求的未知量設為y，設出了未知數(shù)，就可以利用方程思想列出表示等量關系的式子.剩下的過程由學生自己完成后，教師再找個別同學進行板演和講解，最后再讓學生總結(jié)這類問題的求解方法.接著，教師引導學生在已熟悉的內(nèi)容的基礎上進行深度探究，鞏固本章知識，滲透轉(zhuǎn)化思想、數(shù)形結(jié)合思想和分類討論思想，讓學生感悟數(shù)學的直觀、對應和模型思想.教師的適時引領，能激發(fā)學生的內(nèi)省意識，讓學生透過知識感悟問題背后的數(shù)學思想方法，在學生思維的質(zhì)變處精心架起橋梁，為他們今后持續(xù)的學習夯實基礎.

數(shù)學思想方法是數(shù)學學習的內(nèi)在核心.在進行數(shù)學教學時，教師既要注意激發(fā)學生對數(shù)學學習的興趣和熱情，培養(yǎng)學生解決問題的能力和數(shù)學思維能力，又要注意數(shù)學思想方法的滲透，從而使數(shù)學課堂教學更加有效.

責任編輯 張 臻