點上著眼 法上著力 思想是關(guān)鍵

吳從洋 馬嬌嬌

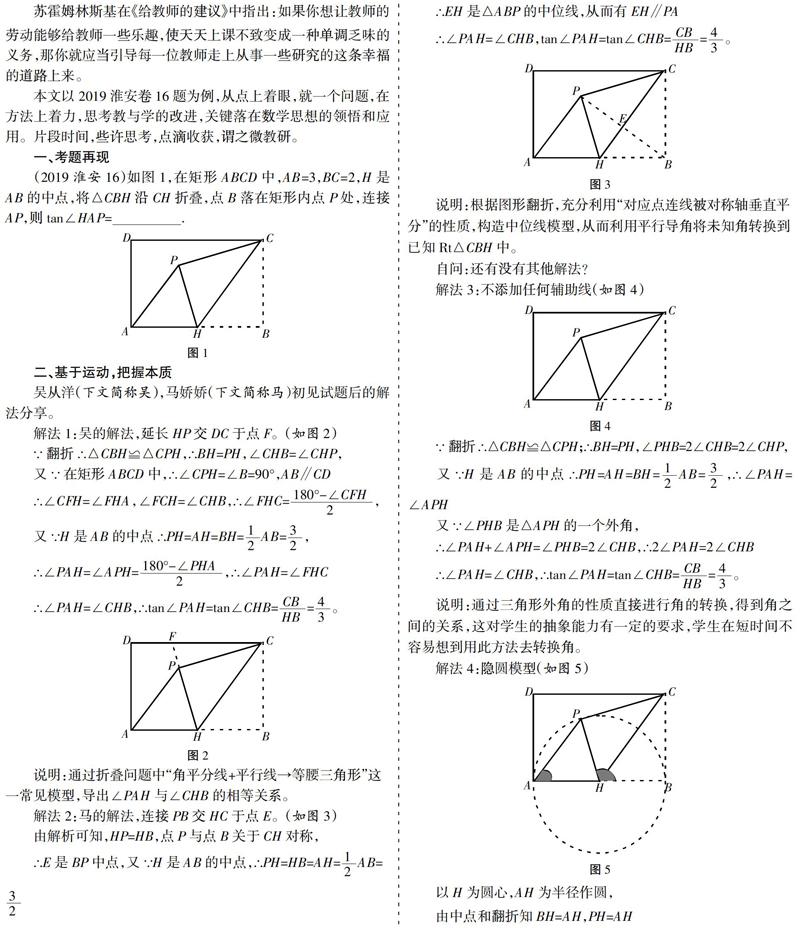
蘇霍姆林斯基在《給教師的建議》中指出：如果你想讓教師的勞動能夠給教師一些樂趣，使天天上課不致變成一種單調(diào)乏味的義務(wù)，那你就應(yīng)當引導每一位教師走上從事一些研究的這條幸福的道路上來。

本文以2019淮安卷16題為例，從點上著眼，就一個問題，在方法上著力，思考教與學的改進，關(guān)鍵落在數(shù)學思想的領(lǐng)悟和應(yīng)用。片段時間，些許思考，點滴收獲，謂之微教研。

說明：當一個圖形中出現(xiàn)共端點3條線段為定長時，通常可以借助構(gòu)造圓來解決問題。當圓出現(xiàn)后，可以運用圓周角定理等有關(guān)知識解決問題。可謂：見等長，現(xiàn)“圓”形。

三、拾級而上，順藤摸瓜

對于學生來說，本道題對學生的抽象能力有一定的要求，如果學生不去分析圖形元素之間的關(guān)系，很容易按部就班在原△APH中構(gòu)造直角三角形，由于原三角形并不是可解三角形，故而需要借助勾股定理、相似等方法求得線段長，會增加解題時間。

下面將學生解題方法列舉一二：

解法5：在解法2的輔助線基礎(chǔ)上，未用E是BP中點這一性質(zhì)。（圖6）

從而根據(jù)同位角相等，也得兩線平行，下同解法2。

說明：看到三條線段相等，便想到可以推導原三角形為直角三角形，再根據(jù)軸對稱的垂直得到直角，從而得出直線平行，進而轉(zhuǎn)角，但未能充分利用“對應(yīng)點的連線被對稱軸垂直平分”這一性質(zhì)，推理略顯復雜。

解法6：利用建系，直接求P點坐標。（如圖7）

說明：建系是一種用代數(shù)方法解決幾何問題的模型，在幾何圖形中，直線就是一次函數(shù)，求線段長可以轉(zhuǎn)化為求解點坐標，但對學生的計算能力要求較高。

還有學生在解法2的輔助線作圖基礎(chǔ)上，結(jié)合勾股定理列方程解題，也有學生構(gòu)造一線三等角模型，利用K型相似求出P所在的直角三角形的兩條直角邊長，但是計算相當冗長。為了讓學生準確定位題目的考點，巧解難題，確實需要教師在教學時引導學生在點上著眼，法上著力。充分抓住運動中的不變量，才能做到妙構(gòu)解法，輕松做題。

四、授之以魚，不如授之以漁

課標中對圖形變換思想提出了具體要求，圖形變換思想是數(shù)學中的一種重要的思想方法，在教學中，向?qū)W生滲透圖形變換思想，能夠幫助學生發(fā)現(xiàn)圖形之間的本質(zhì)聯(lián)系，提高抽象能力，促進思維發(fā)展。近幾年，圖形變換被多個省市選為中考壓軸試題，可見，幾何變換逐漸成為初中數(shù)學的熱點學習內(nèi)容。現(xiàn)以2016年山東威海一題為例加以說明：

如圖8，在矩形ABCD中，AB=4，BC=6，點E為BC中點，將△ABE沿AE折疊，使點B落在矩形內(nèi)點F處，連接CF，求CF的長。

本題解法很多，構(gòu)造中位線模型、等腰三角形模型或一線三等角相似模型，然后借助相似三角形、三角函數(shù)等性質(zhì)解決問題。

識圖、析圖、構(gòu)圖是解決圖形幾何題的關(guān)鍵，遇翻折類問題，最核心的是研究翻折前與翻折后的變化，尤其是抓住翻折過程中的不變量——萬變不離其宗，從而帶來角相等、線段相等等幾何元素的關(guān)系。常見處理策略有：

1.利用全等、垂直、中點等聯(lián)想數(shù)學模型。

2.折疊就有角平分線，結(jié)合平行線，可得等腰三角形模型，結(jié)合等腰三角形“三線合一”定理、倍半角模型等解決問題。

3.如遇直角三角形折疊，可引申出一線三等角模型，借助K型相似，求出未知邊角元素。

總之，充分利用折疊的性質(zhì)，導邊導角，可以妙構(gòu)解法，輕松解題。

通過教師初見試題與學生初見試題后選取的解題思路進行比較，不難發(fā)現(xiàn)學生對于幾何圖形分析能力弱，思維固定，只注重解題，忽略數(shù)學模型的選擇與思想的應(yīng)用。這就要求教師在教學時注重圖形變換思想的滲透，在實際教學過程中，圖形變換思想的滲透不是幾節(jié)專題課就能夠講明白的，而是要借助教材中的多個教學內(nèi)容來完成滲透，這就要求教師平時認真研究教材，適時滲透圖形變換思想。可以借助幾何畫板，演示圖形運動的軌跡，幫助學生形成運動觀念，不斷研究中考優(yōu)質(zhì)題型，以中考題為依托開展課堂教學，注重對優(yōu)秀考題的剖析、研究，關(guān)注解題策略，提高解題能力。

編輯 趙飛飛