拱橋板式吊桿風致渦振特性及等效靜力計算

徐昕宇，王應良，鄭曉龍，陳星宇，曾永平,，唐浩俊

（1.中鐵二院工程集團有限責任公司 科學技術研究院，四川 成都 610031；2.西南交通大學 土木工程學院，四川 成都 610031）

中承式和下承式拱橋的吊桿具有質量輕、長細比大、阻尼比小等特點［1-2］。隨著拱橋跨度不斷增大，拱橋吊桿長度不斷增大，在較低風速下，易產生渦振現象，可能會影響車輛行駛舒適性，造成吊桿疲勞損害，甚至危及橋梁安全［3-5］。

鐵路橋梁要求耐久性高、剛度大，鐵路拱橋常見的剛性吊桿主要為H 型或矩形，但這2類吊桿在一些工程應用中發生過強烈的風致振動現象，如美國Commodore Barry 鋼桁拱橋的H 型吊桿、南京大勝關大橋的空心矩形鋼吊桿，最后只能付出較大的經濟代價通過設置抑振措施抑制風振。國內外研究學者針對這2 類剛性吊桿開展了一系列風致振動研究。Kubo 和Hirata 通過風洞試驗研究了H 型吊桿的抗風穩定性能在均勻流和紊流場中的區別［6］。張龍奇通過節段模型風洞試驗，對斷面為2.4 m×2.0 m 的矩形剛性吊桿的渦振性能進行研究，并對比了截面切角等多種抑振措施效果［7］。

板式吊桿是1 種新型的吊桿型式，目前僅在德國等歐洲國家的部分橋梁中有所應用，其特征為矩形斷面且高寬比較小，一般為1∶6～1∶10。在橋梁設計階段，吊桿的設計通常僅考慮作用在吊桿上的靜風荷載，未考慮吊桿因風致渦振振動產生的荷載動力作用。對于在常遇風速下易發生渦振的吊桿，在經歷長時間的限幅運動后，其力學性能可能難以滿足設計時的要求。目前，針對板式吊桿的風致渦振研究幾乎空白，EN 1991-1.4、《公路橋梁抗風設計規范》等國內外抗風規范中也未考慮吊桿渦振產生的動力作用，相關研究未見考慮渦振性能的吊桿等效靜力計算方法。

本文以拱橋典型板式吊桿為研究對象，采用數值模擬方法，運用動網格技術，建立風致渦振數值模擬模型，通過與已有研究對比，驗證數值模擬方法的可靠性。在此基礎上，進行風向、風速、阻尼比、長細比等因素對吊桿渦振性能影響研究，并基于結果提出板式吊桿考慮渦振動力作用的等效靜力計算方法。

1 渦振數值模擬方法及驗證

1.1 數值模擬方法

為實現風致渦振數值模擬分析，首先將吊桿固定，進行靜止狀態下的數值模擬計算，應用二階格式離散控制方程，采用SIMPLEC 算法計算N—S方程中壓力和速度的耦合問題，對壓力、動量方程、湍流耗散率和湍動能方程采用二階迎風格式進行離散，采用最小二乘的單元格法處理漸變項。待流場穩定后，放松吊桿，提取吊桿的時變側向力，得到吊桿運動響應［8］。運用動網格技術，實現吊桿運動的數值模擬，吊桿的運動使吊桿周圍的流場發生改變，流場的改變會導致作用在吊桿上的側向力產生變化，從而使吊桿的運動響應發生改變。上述過程的循環計算最終可實現吊桿的豎向渦振模擬。

1.2 方法驗證

為驗證本文的數值模擬方法，首先驗證模型靜止狀態的可靠性。斷面根據文獻［9］參數取值，研究對象為矩形斷面，尺寸為0.24 m×0.04 m。

采用流體動力學軟件FLUENT，建立數值模擬模型，并對計算區域進行網格劃分。模型的外輪廓設置為無滑移壁面，計算區域和網格示意如圖1所示。圖中H和D為研究對象斷面垂直和平行于來流方向的尺寸。

圖1 數值模型計算區域及網格劃分圖

基于Newmark-β法，根據所建立模型的質量、阻尼和剛度參數編寫模型的豎向振動的迭代程序，通過用戶自定義函數（User-defined fuction，UDF）在FLUENT求解器中進行編譯。

在體軸坐標系下，斷面三分力系數可表示為

式中：CH，CV和CM分別為體軸坐標系下斷面的阻力系數、側向力系數和力矩系數；FH，FV和FM分別為單位長度結構的阻力、側向力和力矩；ρ為空氣密度；v為來流平均風速；B為斷面的特征尺寸。

斷面靜止時的氣動力系數數值模擬結果與文獻［9］中結果見表1，上表面平均壓力系數Cp=p/(0.5ρv2)（Cp為壓力系數，p為壓力）分布如圖2所示。由表1可見，在雷諾數相近的情況下，本文計算結果與文獻［9］中的風洞試驗和數值模型結果均接近。由圖2可見，本文的二維數值模擬計算結果與研究數據吻合較好，說明本文建立的數值模擬模型能較好地模擬流動分離區域和再附著區域。

表1 氣動力系數對比

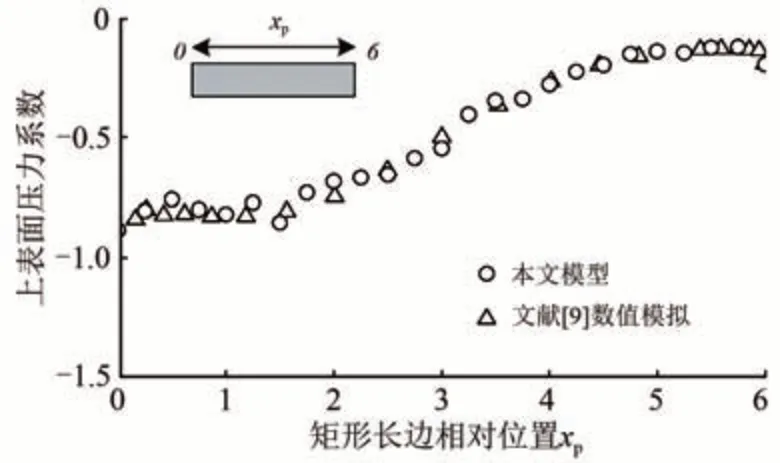
圖2 上表面平均壓力系數分布

為進一步驗證模型運動狀態的可靠性，根據文獻［10］，模型中斷面參數取值為矩形斷面，垂直和平行于來流方向的尺寸分別為0.06 和0.24 m，單位長度質量為3.25 kg，頻率為5.9 Hz，阻尼比為0.58%。分析得到的斷面渦振振幅隨風速變化的渦振數值模擬結果與文獻［10］的風洞試驗結果對比如圖3所示。圖中無量綱振幅為1 000ymax/B，無量綱風速為v/（fB），其中ymax為渦振幅值，f為結構頻率。由圖3可見，本文渦振數值模擬方法得到的分析結果與風洞試驗結果接近，表明本文建立的方法能夠較好地模擬風致渦振。

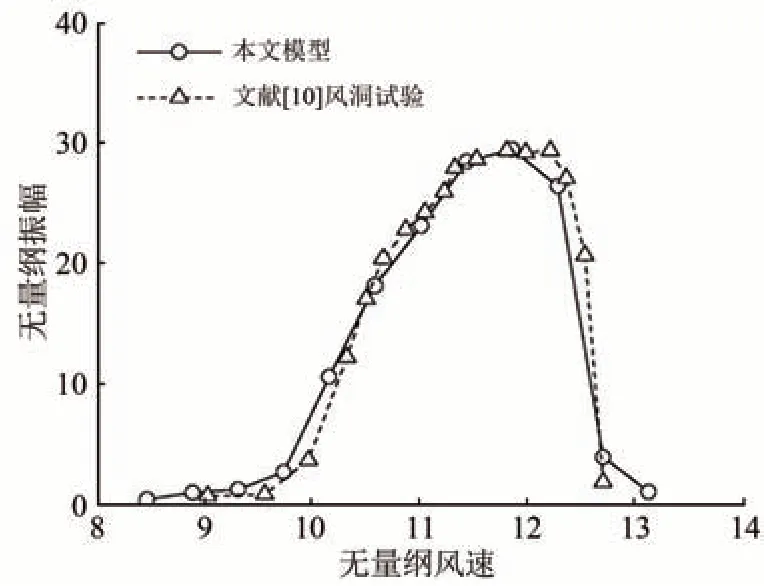
圖3 渦振振幅隨風速變化曲線對比

2 板式吊桿參數對其風致渦振特性影響

研究采用的板式吊桿長邊和短邊的長度分別為0.3和0.05 m，長短邊之比為6∶1。板式吊桿模型計算域包括剛性網格區域、動網格區域以及外部網格區域。計算域內網格總數為31 590個。

由于橋位處風向的不確定性，同時板式吊桿斷面在不同方向上的動力特性存在顯著差異，風向對板式吊桿的動力響應可能有顯著影響。因此，下面以某實際橋梁吊桿為工程背景，研究板式吊桿在短邊迎風和長邊迎風2種情況下的渦振性能。

2.1 短邊迎風

取吊桿單位長度質量為117.75 kg，吊桿長度為10 m，吊桿沿短邊彎曲振動頻率為2.54 Hz，結構阻尼比取0.1%。

2.1.1 風速

板式吊桿氣動性能隨風速變化曲線如圖4所示。由圖4可見：板式吊桿斷面的Strouhal 數（St=fB/v）隨風速無明顯變化，約為0.11；風速為0.9～1.5 m·s-1時，板式吊桿的渦振頻率接近于彎曲振動頻率，可判定此風速區間為渦振鎖定區間；該板式吊桿的渦振振幅最大為1.21 mm，對應的來流風速為1.2 m·s-1，此時的渦振頻率為2.54 Hz，恰好為吊桿沿短邊的彎曲頻率，此時的側向力幅值最大。

0.5，1.2 和2 m·s-1風速下板式吊桿的位移時程及其頻譜如圖5所示。由圖5可見：板式吊桿在各風速下的位移時程均為等幅振動，同時表現出單頻特性。

2.1.2 阻尼比

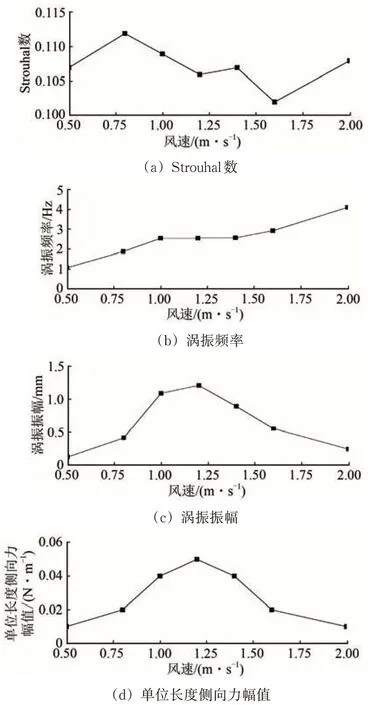
圖4 吊桿氣動性能隨風速變化曲線（短邊迎風）

國內外抗風規范對鋼結構阻尼比的建議取值各不相同。研究計算了不同阻尼比（0.1%，0.3%和0.5%）的板式吊桿渦振性能，分析結果見表2。由表2可見：隨著阻尼比減小，渦振鎖定區間范圍增大，最大渦振振幅大幅增大；同一風速下，側向力幅值無明顯變化；當阻尼比由0.5%減小到0.1%時，渦振振幅由0.13 mm增大到1.21 mm。

2.1.3 長細比

針對10，15，20，25 和30 m 長度的吊桿，進行長細比的影響研究。對應的長細比指吊桿長度與吊桿迎風邊特征尺寸（短邊長度0.05 m）的比值，長細比的范圍為200～600，吊桿的彎曲頻率變化范圍為2.54～0.30 Hz，吊桿頻率隨著吊桿長度的增大而減小。

圖6為短邊迎風時吊桿氣動性能隨吊桿長度變化曲線。由圖6可見：隨著吊桿長度增大，長細比增大，渦振風速、渦振頻率和單位長度側向力幅值均減小，渦振振幅無明顯變化。

圖5 不同風速下吊桿位移時程和幅值譜（短邊迎風）

2.2 長邊迎風

由于吊桿長度相同時，沿長邊風向振動的頻率更高，如果結構振動頻率過大，渦振的數值模擬對時間步長的要求會很高。因此，為在時間步長和計算精度相近的條件下進行對比，長邊迎風時吊桿長度取25 m，吊桿沿長邊彎曲頻率為2.56 Hz。計算中阻尼比選取0.3%。

長邊迎風時吊桿氣動性能隨風速變化如圖7所示。由圖7可見：在長邊迎風情況下，板式吊桿的Strouhal 數隨風速基本不變，約為0.12；在吊桿頻率相近時，相同阻尼比下，長邊迎風的板式吊桿渦振振幅遠大于短邊迎風的板式吊桿渦振振幅。

3 等效靜力計算

在吊桿的設計過程中，一般僅考慮吊桿的靜風荷載，渦振是風作用下的結構動力行為，在吊桿設計時并未考慮其動力效應。上述研究表明，在常遇風速下，吊桿極易發生渦振。為將吊桿渦振的動力效應在靜力分析中考慮，提出1 種考慮渦振的等效靜力計算方法。

表2 不同來流風速、不同阻尼比下吊桿渦振數值模擬結果

圖6 吊桿氣動性能隨吊桿長度變化曲線（短邊迎風）

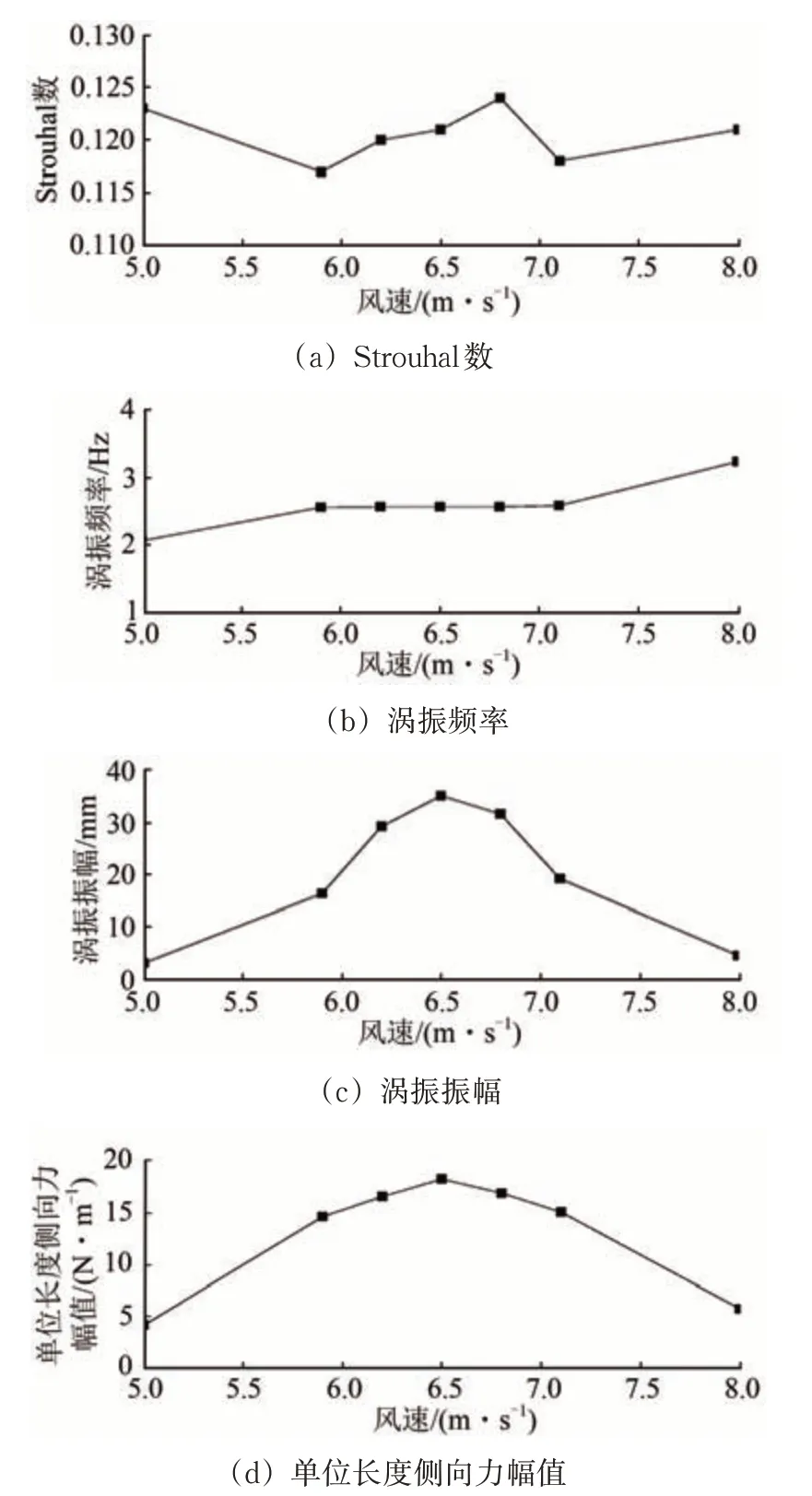
圖7 吊桿氣動性能隨風速變化曲線（長邊迎風）

由圖5可知，吊桿渦振穩定振動表現為單頻等幅運動。針對穩定振動階段，參考Ruscheweyh 建立的渦振力數學模型［11］，可將吊桿所受側向力描述為簡諧力。當結構發生渦振時，側向力頻率、結構運動頻率均與結構固有頻率相等，吊桿的穩態諧振反應振幅ymax可表示為

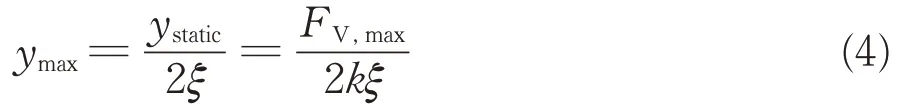
式中：ystatic為靜力位移；FV，max為結構渦振時斷面單位長度側向力幅值；k為結構剛度；ξ為阻尼比。

考慮通過靜力加載簡化，將式（4）等號左右兩端同乘以剛度k，可得

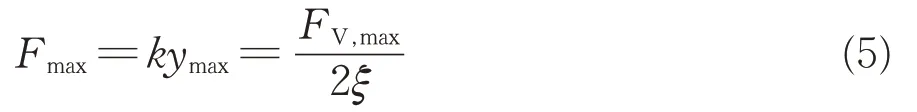
式中：Fmax為斷面單位長度等效靜力幅值。

加載方式按照吊桿的模態振型加載，由于渦振是結構在特定風速區間內發生的特定頻率振動，一般情況下振動對應的振型相對固定。本文考慮彎曲振型，因此，可按均布力在吊桿全長范圍加載，則

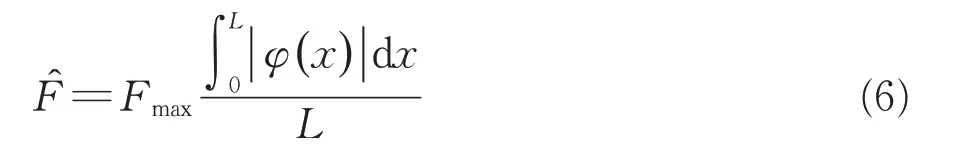
式中：為考慮彎曲振型的單位長度等效靜力；φ（x）為歸一化振型函數；L為吊桿長度。

分析結果表明，同一斷面Strouhal 數基本不變，將Strouhal數和式（2）代入式（6），可得

已有研究表明［12］，當吊桿的彎曲振動頻率在［7，10）Hz 時，吊桿不易發生渦振，考慮引入頻率折減系數μf。風速的增加會導致吊桿特征湍流增加，使完全穩定狀態的相關擾動增大，導致橫向荷載的減少，故引入風速折減系數μv。另外，結合本文分析結果，引入等效靜力修正系數μs，吊桿風致渦振作用的等效靜力計算公式可表示為

其中，

式中：vcr為渦振起振風速。

矩形斷面側向力系數可通過文獻［13］查得。經等效靜力加載試算與前述數值模擬結果進行對比，可得到針對板式吊桿的等效靜力修正系數μs為

4 結 論

（1）建立的風致渦振驗證模型在靜止狀態和運動狀態的分析結果與已有研究的風洞試驗和數值模型的結果進行對比，結果表明，本文建立的渦振數值模擬方法可以較好地重現結構渦振現象，具有較高的可靠性和準確性。

（2）吊桿渦振表現為等幅單頻振動，最大振幅時的振動頻率與吊桿的彎曲振動頻率一致。短邊和長邊迎風時，吊桿的Strouhal 數分別為0.11和0.12。

（3）隨著阻尼比減小，最大渦振振幅增大，渦振鎖定區間逐漸增大。但同一風速下，側向力幅值幾乎無變化。短邊迎風時，當阻尼比由0.5%減小到0.1%，渦振振幅由0.13 mm增大到1.21 mm。

（4）隨著長細比增大，吊桿的渦振風速、渦振頻率以及側向力幅值均減小，但長細比的改變對吊桿渦振的最大振幅無顯著影響。

（5）在吊桿頻率相近時，相同阻尼比下，長邊迎風的渦振起振風速更大，渦振振幅也更大。

（6）通過理論推導和加載試算，提出了板式吊桿作用的等效靜力計算公式，可為拱橋吊桿的靜力分析提供參考。