基于核因子分析的捷聯慣組穩定性評估技術

李 亞, 單 斌, 徐軍輝, 甄占昌

(火箭軍工程大學導彈工程學院，西安 710025)

隨著慣性技術的快速發展，以及慣性導航不依賴外部信息的獨特優勢，捷聯式慣性測量組合在航空航天、戰略戰術導彈及民用領域得到了廣泛的應用[1]。穩定性是評價捷聯慣組性能狀態的重要作戰指標，捷聯慣組的穩定性是否合格決定了其能否被使用，但是受制造工藝、使用情況(通電時間、存儲時間、溫度、氣壓等)的影響，目前捷聯慣組的穩定性較差。為了保證其使用性能，必須采用定期循環測試方案，且穩定性評估的結果僅有“穩定”和“不穩定”兩項，存在太過單一、無法量化的缺點，不能給使用單位選用捷聯慣組提供足夠的信息支撐，極大地影響了捷聯慣組的使用效率。

陳效真等[2]提出了一種利用大數據理論對慣組全壽命周期內的海量測試數據進行充分挖掘、分析與應用的數據分析平臺的基本框架，但該框架中僅是一個雛形，其中數據挖掘、數據分析等關鍵技術還有待進一步展開深入的研究。當前，以慣組為主體進行狀態評估的研究還比較少。但在旋轉機械、機電設備等領域，基于數據驅動的狀態評估已經得到廣泛的應用。葛蒸蒸[3]等對彈上產品加速退化過程建模,然后利用方差-協方差矩陣研究了一種彈上產品的可靠性評估方法；陳建春等[4]利用時序主成分分析研究了捷聯慣組的穩定性隨時間序列變化的狀況；鄧超等[5]等基于維納過程對某數控機床進行性能退化建模，然后用逼近理想解法和馬氏距離實現了對該設備的健康狀態評估。

因子分析(factor analysis, FA)[6]是主成分分析(principal component analysis, PCA)[7]的拓展，它與主成分分析最大的不同在于降維得到的各因子具有可解釋性。利用同一批次，同一履歷的捷聯慣組在性能上相似的特點，改進了傳統的因子分析方法，利用統計學習中的核化原理將其拓展為一種非線性特征提取方法——核因子分析(kernel factor analysis, KFA)，并基于核因子分析提取的特征進行了因子綜合評價，實現了對捷聯慣組的穩定性評估。基于KFA的捷聯慣組穩定性評估方法流程見圖1。

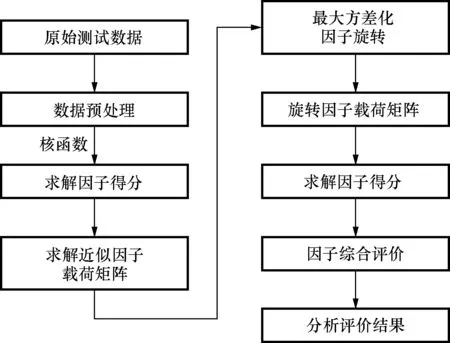
圖1 基于核因子分析的綜合評估方法Fig.1 Comprehensive evaluation method based on KFA

為了檢驗該方法的正確性和實際效果，推導了KFA中因子得分和因子載荷矩陣的求解過程，證明了KFA的合理性；利用K最鄰近分類算法(K-nearest neighbor,KNN)[8]對基于KFA的捷聯慣組穩定性評估結果與其他評價方法進行了對比，分析了其有效性和不足。

1 因子分析模型

因子分析的基本思想是通過分析多變量間的相關矩陣，找到支配變量間相關關系的少數幾個相關獨立的潛在因子，達到簡化觀測數據，用少數變量解釋研究復雜問題的目的[9]。因子分析的一般模型為

X=AF+ε

(1)

式(1)中：X=[X1,X2,…,Xm]T為標準化的觀測變量；AF稱為公共分量，表示各個觀測變量的共性信息；ε=[ε1,ε2,…,εn]為特殊因子分量，表示各個觀測變量不能被公共因子解釋的部分；F=[f1,f2,…,fr]T為公共因子向量；A=[aij]m×r為因子載荷矩陣，aij為變量Xi在公共因子fi上的載荷，它反映了公共因子fi對變量Xi的重要程度。

與主成分分析不需要假設條件不同，因子分析的一般模型基于以下假設[6]。

(1)E(F)=0,即各因子的均值為零，其中E表示均值。

(2)Cov(F)=E(FF′)=I，即各公共因子互不相關，其中Cov表示協方差。

(3)Cov(F,ε)=0，即各公共因子與特殊因子互不相關。

(4)E(ε)=0，即各特殊因子的均值為零。

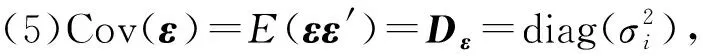
2 核因子分析及穩定性評估

通過核函數使線性數據處理拓展到非線性數據處理的方法已得到廣泛應用，典型的運用有核主成分分析、核獨立成分分析、Fisher核判別分析等[10]。

傳統因子模型的求解方法主要有極大似然估計法、主因子法和主成分法等，前兩者都是基于相關矩陣求解的，但核空間中的相關矩陣不易求解；而主成分法既可以通過相關矩陣求解，也可以通過協方差矩陣求解。因此先用核主成分分析求解出原始觀測變量在核空間中的主元，標準化后作為因子得分，再利用多元線性回歸求出近似因子載荷矩陣用于解釋各因子的意義，然后采用最大方差化方法進行因子旋轉，求解旋轉后的因子得分再進行綜合評價。

2.1 基于KPCA的因子得分求解

假設Xm×n為一個經過標準化處理后的有m個變量、n個樣本的“相關變量集”。將原輸入空間映射到一個高維的特征空間F中進行因子分析。假設映射數據為零均值，則Xm×n經過非線性映射在F空間數據的協方差矩陣為

(2)

式(2)中：Φ(·)為進行非線性變換時使用的非線性映射函數。

假設協方差矩陣CF的特征值為λ，對應的特征向量為V，可得:

λV=CFV

(3)

將式(3)兩邊乘以Φ(xk)，式(3)可等價為

λ〈Φ(xk),V〉=〈Φ(xk),CFV〉,k=1,2,…,n

(4)

根據核再生理論，存在系數αi,使得CF的特征向量V可由Φ(xi)線性表示：

(5)

由式(3)、式(4)可得：

(6)

定義核陣K，令Kij=〈Φ(xi),Φ(xj)〉，則式(6)可以等價為

λnα=Kα,α=[α1,…，αn]T

(7)

令〈Vk,Vk〉=1，則

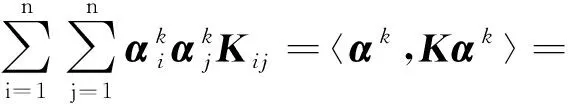
〈αk,λknαk〉=1

(8)

則樣本的第k個主元為

(9)

由于在實際應用中映射數據為零均值的條件不是永遠成立的，所以需要做如下式的中心化處理：

(10)

式(10)中：(1n)ij=1/n,(i,j=1,2,…,n)。

(11)

(12)

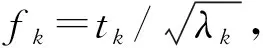
2.2 基于多元線性回歸的因子載荷求解

所求fk為因子得分，由于映射數據的維數與大小是未知的，故F空間中的因子載荷矩陣A不可解。對這一非線性關系線性化，基于多元線性回歸求解近似因子載荷矩陣。其關系式表達為

Xi=ui+(ai1,ai2,…,air)(f1,f2,…,fr)T+Δ

(13)

式(13)中:Xi為標準化的第i個觀測變量；ui為截距；(ai1,ai2,…,air)為線性近似因子載荷矩陣的第i行；(f1,f2,…,fr)T表示樣本在一定貢獻率下各因子對應的因子得分；Δ表示殘差。

主成分法確定的因子載荷不完全符合因子模型的假設前提，但當共同度較大時，特殊因子所起的較小，特殊因子之間的相關性所帶來的影響幾乎可以忽略[6]。當ui和ε很小時，忽略其對整體的影響，可以認為所提出的核因子分析滿足因子分析模型的假設(3)～假設(5)。

多元線性回歸本質上是利用最小二乘法使得殘差最小，殘差越小，擬合效果越好。所提出的近似因子載荷矩陣的擬合效果可以用模型的貢獻率G表示，如式(14)所示：

(14)

式(14)中：p為觀測變量的維數；r為因子數目;aij為近似因子載荷矩陣的元素。貢獻率G越大時，殘差越小，說明近似因子載荷矩陣解釋的信息越多。

2.3 因子綜合評價

因子綜合評價是指以各因子的方差貢獻率為權，由各因子的線性組合得到綜合評價函數對樣本進行評價的方法，表達式為

W=w1|f1|+w2|f2|+…+wr|fr|

(15)

式(15)中：wi為第i個因子的貢獻率，fi為第i個因子的因子得分；W為綜合評價結果。

fi實際上是各觀測變量降維后的結果，它的絕對值大小反映了穩定性的大小，同時考慮到各個因子的貢獻率之和不為1，不利于比較，取穩定性評價函數W為

(16)

3 實例分析

實驗數據來自同一批次，同一履歷的16套捷聯慣組，剔除嚴重超差的測試數據之后，共有116組用于穩定性判斷的數據，其中穩定的有84組，不穩定的有32組。考慮到不同誤差系數的穩定性會隨儲存時間的變化而變化，故每組用于穩定性評估的數據為兩次測試間的時間差和各誤差系數(共33個)之差。使用的核函數為高斯徑向基(RBF)核函數[11]:

K(x,y)=exp(-‖x-y‖2/σ2)

(17)

3.1 核參數的選擇

高斯核函數只有一個可調參數σ，圖2為提取核空間內原始數據最低貢獻率85%時因子數目隨σ的變化情況，它表明核因子分析的降維效果在特定樣本總體下是有限的。

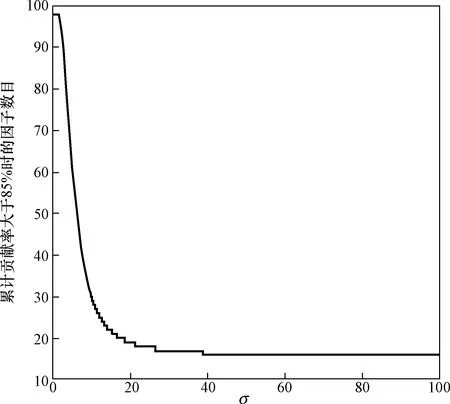
圖2 最低貢獻率為85%時的因子數目Fig.2 Number of factors with a minimum contribution rate of 85%

構建函數F(σ)=(sσ1+sσ2)/sb，sσ1、sσ2分別為穩定數據、不穩定數據核映射后的類內離散度，sb為兩類數據核映射后的類間距離平方和，F(σ)可以用來表示一定核參數兩類數據非線性可分程度。大量實驗研究表明，在解決完全非線性可分的問題時存在著極小值點[12]。圖3為F(σ)隨著σ的變化，當σ取9.45時，F(σ)取得最小值，穩定數據與不穩定數據在核空間里最大程度非線性可分，但由于σ取較小值時降維后的因子數目較多，不利于解釋各個因子的意義。選擇因子數目為16，此時F(σ)最小時對應的σ為38.87。

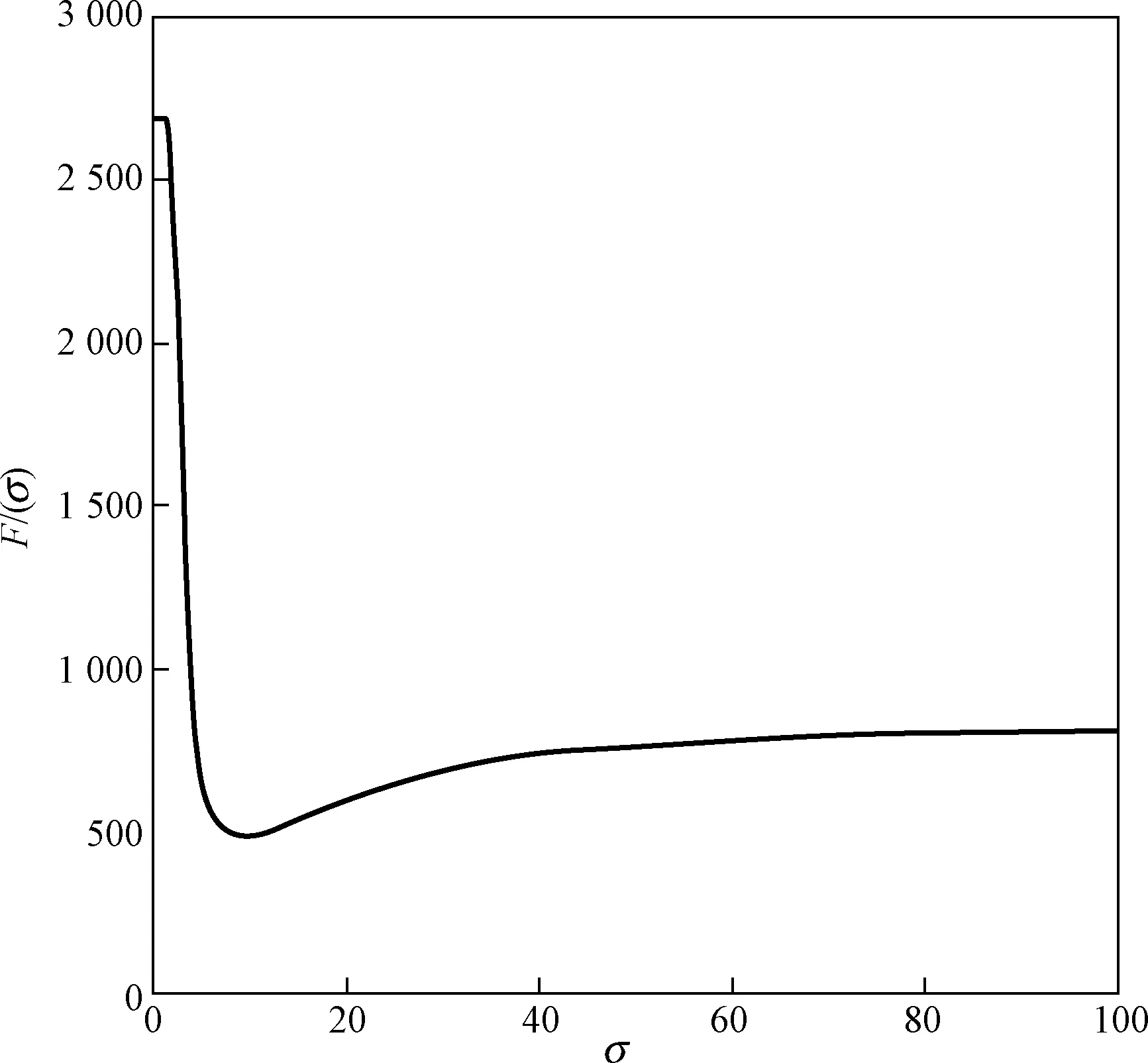
圖3 F(σ)變化曲線Fig.3 Change curve of F(σ)

3.2 因子解釋

表1為部分的旋轉成分矩陣。由表1可知，所提出的KFA方法降維后的各因子在方差最大化旋轉后，具有較好的可解釋性。

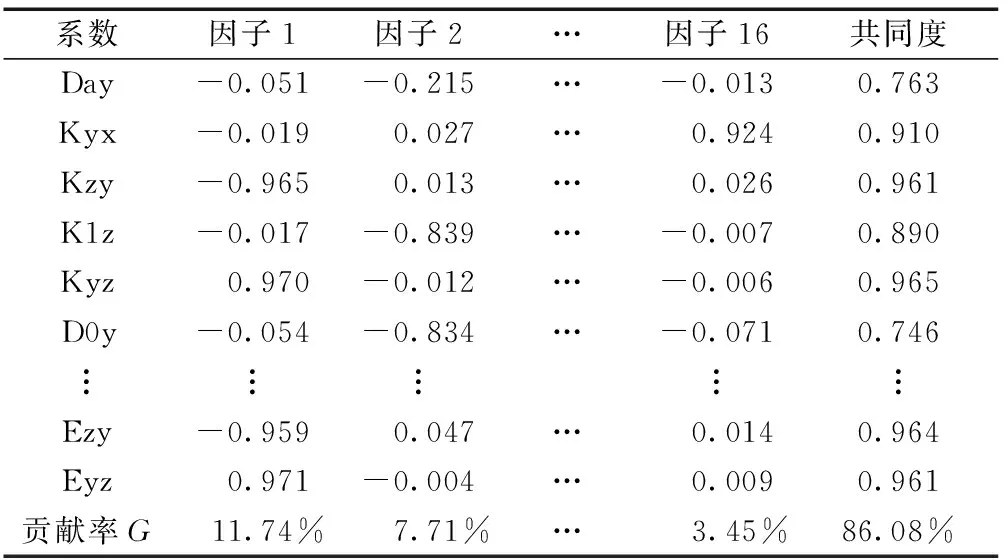
表1 旋轉成分矩陣Table 1 Rotation component matrix

3.3 穩定性評價及結果分析

圖4為所有樣本的穩定性評價結果，其中前84個為穩定樣本，后32個為不穩定樣本。從圖4可以看出，評分較低的主要是不穩定樣本，但也存在一些不穩定樣本的評分較高。

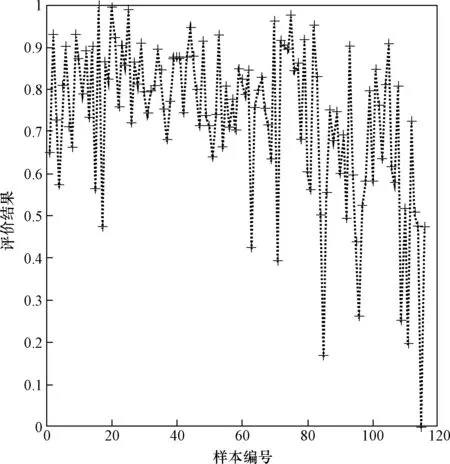
圖4 KFA綜合評價結果Fig.4 Result of KFA comprehensive evaluation

3.4 穩定性評估效果評價

為了對比提出的基于核因子分析的捷聯慣組穩定性評估方法，將核因子分析與因子分析、熵值法兩種方法進行了比較。采用KNN[13]這一經典分類算法分析不同的評估方法對于穩定樣本和非穩定樣本的的區分能力。為了取得相對穩定的結果，取100次十折交叉驗證的平均正確率為指標；針對兩類樣本數目嚴重不均衡的問題，對算法中的投票原則[14]進行了調整使得其與兩類樣本的數目之比一致；KNN使用的距離量度為歐氏距離。

3.4.1 熵值法

熵值法[15]是一種絕對客觀的賦權方法，它的評價過程完全依賴于客觀的數據規律，從而很大程度上避免了人為因素的影響。

在熵值法中進行異質指標同質化時，采用負向指標進行歸一化，即各誤差系數的變化值越小，穩定性越好。

在熵值法中，第i個指標的權重為

(19)

式(19)中：di、Hi分別為第i個指標的偏離度和熵值。

3.4.2 結果分析

圖5為原始數據-熵值法評估方法、因子分析評估方法(16個因子、貢獻率為86.92%)、KFA評估方法(σ取38.87，16個因子，貢獻率G為86.08%)的分類正確率比較圖。在圖5中，K大于30時3種方法的平均正確率都趨于穩定，并且在K大于60時平均正確率幾乎一致；當K為30～60時，熵值法的評估效果要較好于KFA法和因子分析法，這是由于熵值法使用了原始數據，而其他兩種方法在降維后失去了部分原始信息；KFA法和因子分析法的評估效果近乎一致，且都與熵值法的評估效果差別較小，這說明提出的基于KFA的捷聯慣組穩定性評估方法是合理的。

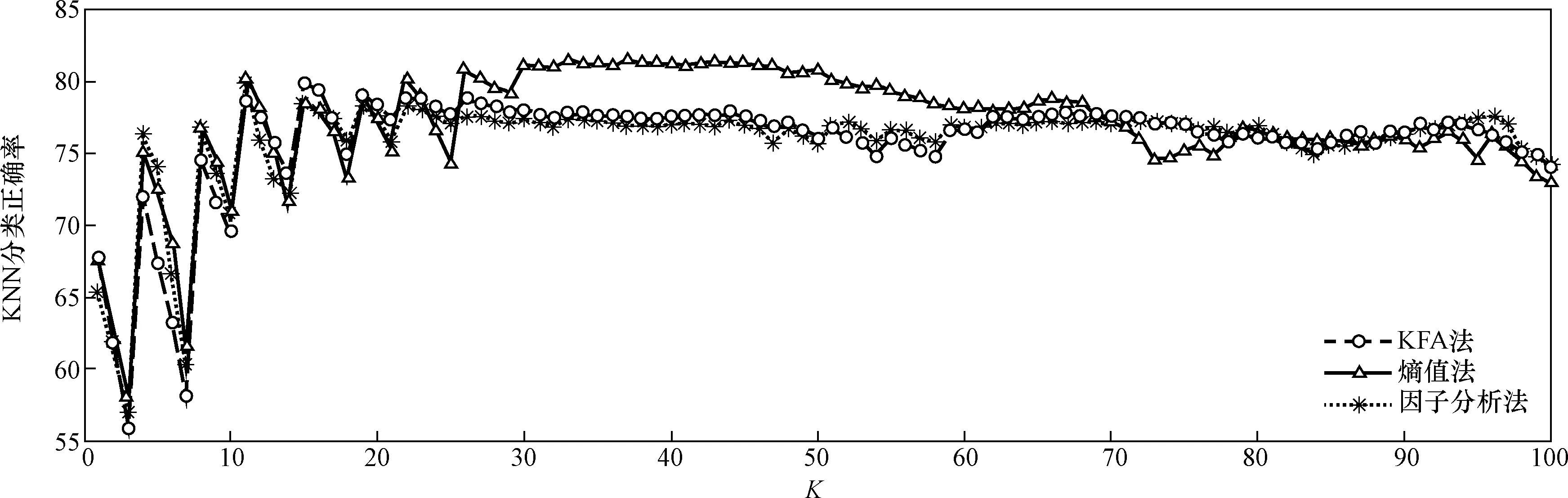
圖5 KNN分類結果Fig.5 Result of KNN classification

當K接近于交叉驗證的訓練樣本數時，3種方法的分類正確率都逐漸穩定在77%左右。這是由于這3種方法都是只利用數據客觀規律的方法，即穩定性評估效果最好的樣本是樣本總體里各觀測變量變化最小的一個，但這并不能嚴格地與穩定性指標各個閾值的評價結果完全一致。

相對于熵值法不能用于降維的缺點和因子分析只能提取線性特征的不足，提出的KFA法具有能較好地提取原始變量的非線性特征并解釋其含義的優點，比較適用于非線性關系較強的數據集。

4 結論

對捷聯慣組的穩定性進行評估能更好地幫助使用單位了解捷聯慣組的穩定狀態，從而提高使用的效率。提出的基于核因子分析(KFA)的捷聯慣組穩定性評估方法，從理論上證明了該方法能夠滿足因子分析的5個假設條件，并將其與熵值法和傳統的因子綜合評價方法進行了比較，證明了其有效性。

KFA方法的不足在于不能較好地與穩定性指標結合起來，將穩定與不穩定兩種狀態的捷聯慣組完全區分開，實際上這也是熵值法等客觀評價方法的共同存在的不足。下一步，可以將KFA法與其他主觀評價方法結合起來，以取得更好的穩定性評估結果。