基于滾石運動參數的防護網數值模擬

劉成清， 陳玉滿

(西南交通大學土木工程學院，成都 610031)

滾石在自重以及外力作用下脫離母體或原位，以自由落體、拋射、彈跳、滾動、滑動或以多種運動方式的組合形式順坡向下運動，沖擊公路、鐵路等沿線，威脅行車及人身安全。被動柔性防護網因其“以柔克剛”的結構性優勢功能，被廣泛運用于工程實踐的有效防護措施之一。何思明等[1]給出了滾石碰撞具體的計算公式；章廣成等[2]研究了碰撞恢復系數的特征及影響因素；馮曉等[3]基于概率統計理論對滾石運動軌跡進行模擬；陳穎騏等[4]基于Hertzj接觸力學和Thornton彈塑性假設建立了滾石對構造物的沖擊力修正方程；葉四橋等[5]研究表明滾石質量、坡面狀態、坡度、下落高度對切向恢復系數影響較大；許婧璟等[6]基于能量跟蹤法研究巖石破碎對運動軌跡影響；Hambleton等[7]考慮“子彈效應”提出被動柔性防護網臨界動能的數值模型；Tran等[8]進行了試驗與數值仿真結果表明數值仿真可以代替試驗進行防護網設計選型；劉成清等[9-12]、Liu等[13]和Yang[14]研究了被動柔性防護網的整體變形以及減壓環、鋼柱等關鍵構件的耗能及其破壞機理。目前對柔性防護體系中網片、消能件及鋼絲繩網等組件研究較多。對滾石滾動的某個階段如碰撞基于理論與試驗也有報道，但對滾石整個運動階段的理論與試驗研究相對較少，基于確定的滾石運動參數被動柔性防護系統研究目前也很少。基于接觸理論和動力學理論對滾石從初始運動階段到最終停止進行了理論推導，對影響滾石運動狀態的坡度與坡面材料展開研究，利用成熟的滾石模擬軟件獲取可以用于設計的運動參數。利用ANSYS/LS-DYNA對落石撞擊網片進行數值仿真驗證選型合理性。

1 滾石運動狀態

典型的滾石運動狀態一共經歷五種運動情況分別為自由落體運動、拋射、碰撞、 滾動滑動，如圖1所示。

h1為滾石自由落體的高度；h2為滾石斜拋上升的高度；h3為斜坡上碰撞下降的高度；α1為第一段斜坡的坡度；α2為第三段斜坡的坡度；α1為第一段斜坡的坡度；l1為滾石發生碰撞到滾動滑動階段水平位移；l2為滾石滾動滑動到停止運動階段水平位移圖1 滾石運動示意圖Fig.1 Rolling stone motion diagram

1.1 自由落體階段

滾石的自由落體運動，是在重力作用下脫離母巖， 也或者在只有一定的初始角速度開始運動，大部分是啟動階段中的墜落或者傾倒導致。由于空氣阻力一般只有重力1/20左右，故一般忽略不計，角速度在墜落過程中則認為保持不變，滾石運動軌跡公式為

(1)

(2)

式中：h1為自由落體的高度；g為重力加速度，g=9.8 m2/s;v為滾石的下落速度。

1.2 碰撞階段

以 Hertz 接觸力學為計算基礎，假定滾石為剛性體，碰撞時地面只發生法向變形，切向未發生變形。將碰撞過程分為兩個階段：壓縮階段和回彈階段。壓縮階段指落石從與地面接觸到壓縮地面產生最大的彈塑性變形過程，分為彈性加載階段與塑性加載階段；回彈階段指從最大彈塑性變形位置彈性恢復至殘余塑性變形位置的過程即回彈卸荷階段。碰撞過程假定滾石與坡面的碰撞發生在一個碰撞點上,不產生滑移。Azzoni等[15]研究結果也表明碰撞過程滑移確實極少發生。

1.2.1 彈性加載階段

接觸力學[16]中Hertz應力分布函數：

(3)

法向位移函數：

(4)

位移邊界條件：

μz1+μz2=δ-(1/2R)r2

(5)

將式(4)代入式(5)中，得：

(6)

由牛頓第三定律：

(7)

式中：

a=πp0R/2E*

(8)

(9)

(10)

滾石對地面的荷載為

(11)

聯立式(7)～式(11)得：

(12)

式中：μz1、μz2分別為碰撞前后法向位移；E*為滾石與地面接觸的等效彈性模量；p0為最大接觸應力；a為接觸區半徑；r為距離接觸區中心的距離；R為滾石與坡面的等效半徑；δ為貫入量；E1、E2分別為滾石和坡面的彈性模量；ν1、ν2分別為滾石和坡面的泊松比；R1、R2分別為滾石和坡面的等效半徑。

Jackson 等[17]研究的彈塑性材料應力與滾石砸入深度間的關系：

(13)

C=1.295e0.736v

(14)

Cσy=min[C(v1)σy1,C(v2)σy2]

(15)

聯立式(13)～式(15)可得：

(16)

由能量守恒定律：

(17)

聯立式(16)和式(17)得：

(18)

式(18)中：σy1、σy2為碰撞前后的屈服應力；V為土體第一次屈服時的瞬時速度；C為臨界屈服應力系數；V2為滾石碰撞后的速度；δy為土體初始屈服時的貫入量；σy為土體的初始屈服應力。

1.2.2 塑性加載階段

(19)

V3=0，此時滾石達到最大砸入深度，有：

(20)

基于土體的線彈性本構得：

Pep=σy

(21)

(22)

聯立式(20)～式(22)得：

Fy(δm-δy)

(23)

式中：Pep為塑性加載階段的接觸應力；V為瞬時速度；Vy為彈性階段過渡到塑性階段的臨界速度；W*為塑性加載階段的應變能。

1.2.3 回彈卸荷階段

回彈卸荷階段土體的應力應變關系與彈性階段保持一致。

(24)

(25)

式中：Prep為回彈卸荷階段的荷載；V2、V1分別為碰撞后和碰撞前的速度；δ為塑形殘余變形；δm為最終變形量。

法向的恢復系數為

(26)

根據胡厚田等[18]的研究, 考慮瞬間摩擦的作用, 切向速度大小在碰撞過程中損失率約為10%，切向恢復系數et可考慮的坡面材料進行適當取值，et為0.8～1。

1.3 拋射階段

由于空氣阻力只占到滾石重力的1/20左右，通常忽略不計，假設滾石剛經過碰撞后獲得速度V2，經過拋射運動后的速度為V3，h3為滾石斜拋初始點與落點的高度差，h2為滾石初始點與最高點的高度差，θ為拋射角度。根據能量守恒定律：

(27)

(28)

水平位移：

(29)

1.4 滾動滑動階段

滾動、滑動階段即滾石在自重作用下考慮斜坡的滾動/滑動摩擦沿著坡面向下運動，滾動、滑動階段運動狀態相似，一般是滾石運動停止的最后一個運動階段，可由運動學知識獲得滾石滾動階段的加速度：

a=(gsinα-gkcosα)

(30)

滾動階段的瞬時速度變化：

(31)

滾動階段的能量變化：

(32)

k=tanΦd

(33)

(34)

式中：V4為滾石滾動前的速度；α為斜坡坡角；a為滾動、滑動階段加速度；k為滾動摩擦系數/滑動摩擦系數；Φd為摩擦角；s為滾動距離；sm為停止滾動距離。

2 滾石運動狀態的影響因素

2.1 碰撞與拋射滾動能量耗散比較

1.2～1.4節給出了碰撞、斜拋及滾動滑動階段的速度能量計算公式，由于δreu需要試驗測得，采用已經成熟的滾石運動軌跡模擬軟件Rocfall軟件進行模擬。簡化模型，選取一端坡度為45°的斜坡進行模擬，通過設置初始速度使初始動能保持一致，比較三者的能量損耗差異。滾石的初始質量為10 kg。坡面材料為基巖露頭的恢復系數取值采用Rocfall軟件默認取值，法向恢復系數為0.35，切向恢復系數為0.85，摩擦角為21.8°[16]。如表1所示基巖滾動摩擦系數為0.40，利用式(32)求得。滾石運動軌跡如圖2所示，能量變化如圖3所示。

表1 滾動摩擦系數[16]Table 1 Coefficient of rolling friction[16]

圖2 滾石運動軌跡Fig.2 Rolling stone movement track

圖3 滾石動能變化Fig.3 Rolling stone kinetic energy change

運動軌跡與能量變化顯示斜拋碰撞階段先做拋物線型然后陡降，滾動階段能量圖顯示直線均能一定程度上驗證第1節推導公式的合理性。滾石第一次撞擊損耗的能量336.9 J，第二次撞擊損耗的能量315 J，到達x=20 m時，滾石做斜拋碰撞運動的動能為 1 415.6 J，做滾動時為1 400 J，說明滾動階段所造成的能量損耗要比斜拋碰撞階段要大。

2.2 坡度對碰撞，拋射，滾動的影響

l為水平總坡段的長度，l=180 m；h為坡段總高度，h=180 m；d為水平分段長度，d=60 m，滾石的初始運動參數為水平速度為10 m/s，豎直速度為10 m/s方向向上，滾石初始質量設為10 kg。邊坡材料均為基巖裸露材料參數2.1節已說明。滾石在不同坡度的運動軌跡如圖4所示，能量變化如圖5所示。

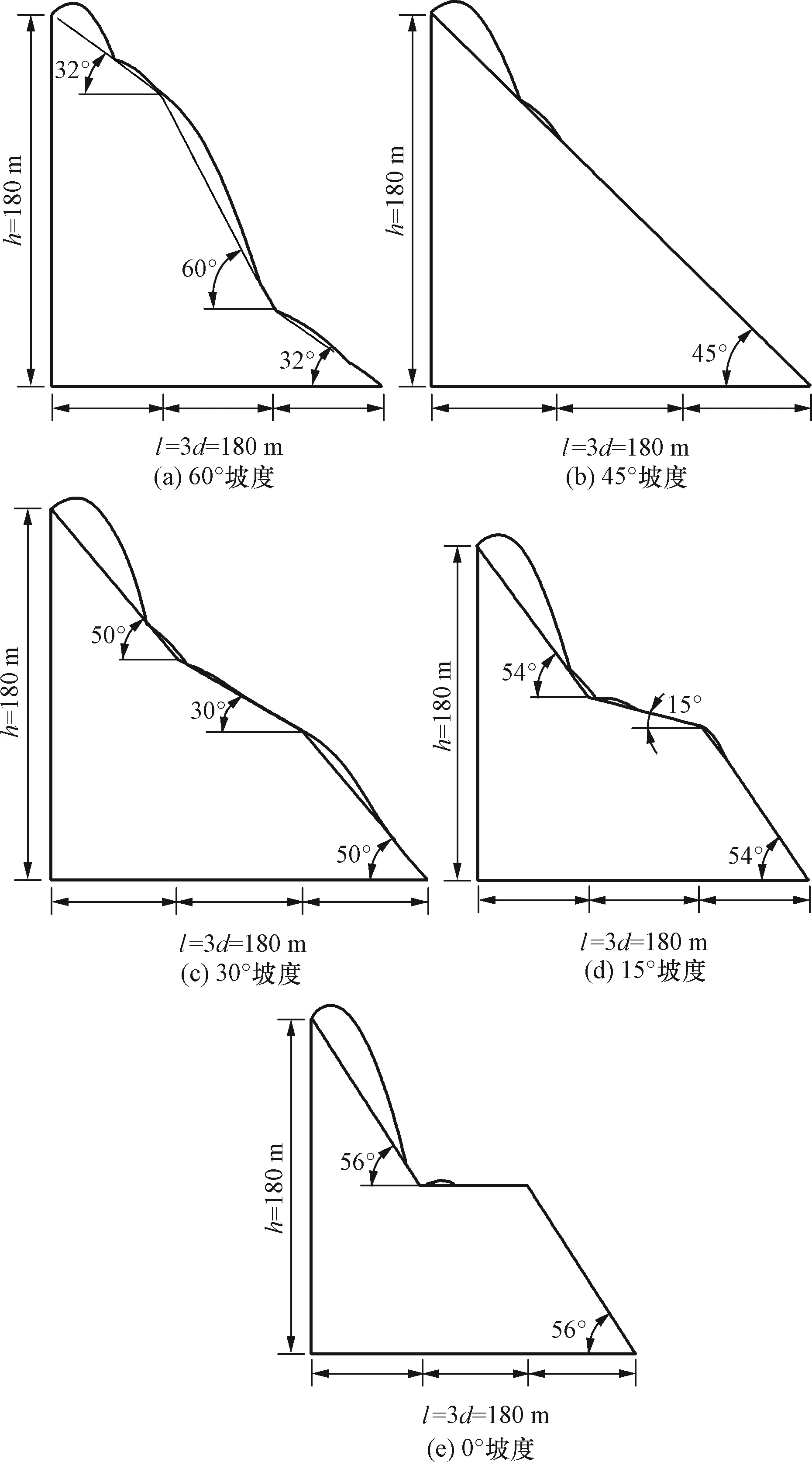
圖4 不同坡度滾石運動軌跡Fig.4 Rolling stone movement track at different slopes

圖5 不同坡度滾石動能量變化Fig.5 Dynamic energy change of rolling stones with different slopes

如表2所示，不同坡度中，以中間坡段45°坡度作為參照，中間坡度為30°，60°時，造成的動能損耗基本一致損耗差別僅為26.7 J，兩者滾石的運動軌跡也大致相同，而全部坡段坡度均為45°的坡段所造成的能量損耗最少，與中間坡段坡度為60°相比，動能損耗差別為2 897.3 J，設置了平臺的斜拋滾石能夠有效較少碰撞次數提前終止運動。中間坡度為60°、30°的斜拋可以概括為兩緩一陡坡段和兩陡一緩。能加大滾石能量的損耗。

表2 滾石碰撞次數及能量Table 2 Number of rolling stone collisions and energy

2.3 坡面材料對碰撞，拋射，滾動的影響

表3的恢復系數取值采用Rocfall軟件默認取值，摩擦角取自文獻[16]。

表3 邊坡材料參數Table 3 Material parameters of slope

如圖6所示，清潔基巖面和土壤與植被覆蓋的邊坡能減少碰撞拋射的次數，采用土壤和植被材料所覆蓋的坡面能損耗滾石的能量最大，相比其他坡面材料使滾石提前停止運動，清潔基巖覆蓋的坡面所造成滾石能量的損耗相比其他坡面要少得多，相比基巖露頭、土壤植被覆蓋的坡面，其他坡面材料覆蓋的坡面最終對滾石的能量損耗大致相同，且三者的運動狀態也基本一致。基于土壤和植被材料所覆蓋的坡面對滾石能量影響最大，可考慮在坡面表面鋪設土壤與植被增加滾石動能的損耗。

圖6 坡面示意與能量變化Fig.6 Slope indication and energy change

3 滾石運動參數

3.1 案例與模型

邊坡位于滇池盆地西北部邊緣，屬于崩塌堆積地貌。選取危巖體高程位于 2 125～2 155 m，與高速公路路面高差最大達260 m，屬于特高位危巖體。呈不規則塊狀，該危巖體下部存在凹腔，屬于懸挑式崩塌危巖體。在地震作用下發生崩塌剝落，對行車安全與人身安全危害極大。考慮不安全因素假設因地震作用造成質量為50 kg的滾石墜落，初始速度設為0，選取模擬滾石次數為 1 000。起始運動為滾動。

3.2 運動軌跡

圖7為滾石的運動軌跡及一般防護裝置布置位置。

圖7 滾石運動軌跡Fig.7 Rolling stone track

3.3 滾石彈跳高度、能量、速度參數

從圖8可以看出,滾石的起始做滾動運動，在經過碰撞斜拋運動離開斜坡，在水平位置69.7 m左右達到彈跳的最大高度，此時距離斜坡5.5 m，接著做向下的斜拋運動水平位置242.4 m時離斜坡的高度達到15.5 m，最后在水平位置260.6 m時落到公路上彈跳高度達到17.1 m。滾石的總動能變化，在水平位置為75.8、130.3、254.5 m時，滾石的總量分別達到34.2、50.4、38.5 kJ。一般的防護裝置均設在公路邊緣附近，但在這些位置攔截時攔截難度較大。

圖8 滾石彈跳高度及能量分布Fig.8 Rolling stone bounce height and energy distribution

不利于防護裝置發揮最大耗能，且彈跳高度較高已超過防護裝置的防護范圍，而水平位置130.3～215.2 m時，滾石總能量呈現減小的趨勢，在水平位置151.503 m的滾石能量與速度較低，可有效降低防護網因為子彈效應造成的穿透，故此處設置被動防護網裝置較為合適，滾石在此位置的動力參數分布如圖9所示。

如圖9所示，滾石的速度主要集中在14.75～32.99 m/s，29.95 m/s時滾石數目為303，占比30.3%，滾石的彈跳高度分布在0～2.72 m，1.60～1.74 m滾石數目分布為173。被動柔性防護裝置網片易因子彈效應[7]被擊穿，取滾石速度32.99 m/s，滾石最大彈跳高度為2.72 m。

圖9 x=151.503 m彈跳高度與速度分布Fig.9 x=151.503 m bounce height and velocity distribution

4 滾石災害治理

被動柔性防護網因其“以柔克剛”的結構性優勢功能，是治理滾石災害的有效防護措施之一。基于被動柔性防護網裝置大部分是網片破壞，簡化模型建立網片以及支撐繩系統。基于獲取的滾石運動參數及彈跳高度分布，滾石質量為50 kg，考慮安全儲備運動速度取34 m/s，基于滾石彈跳高度最大2.72 m選用3.3 m×6.6 m環形網，網型選用R7(7圈環繞)/3 mm/300 mm較為合適，等效截面半徑26.42 mm2，支撐繩半徑8 mm，等效截面面積200.96 mm2，利用ANSYS LS-NYNA進行數值仿真分析，材料參數如表4所示。

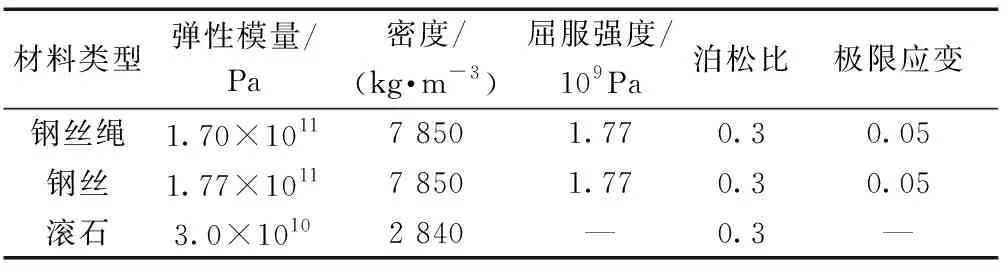
表4 材料參數Table 4 Material parameter

從圖10可以看出，滾石砸在防護網的中心位置，在網片中心位置最大豎向位移為2.30 m，且未發生破壞，在滾石質量較小的情況下，能阻止較高速度的滾石沖擊，避免對過往車輛造成嚴重危害，說明基于滾石運動參數的防護網選型合理能有效防治滾石災害。

圖10 滾石防護網模型及仿真Fig.10 Rolling stone protective net model and simulation

5 結論

基于Hertz接觸力學、運動學公式，對滾石運動各階段運動公式進行了推導分析，研究了坡度、坡面材料對滾石運動狀態及能量損耗的影響，通過工程案例分析獲取了滾石災害防治所需的運動參數與彈跳高度，利用數值仿真軟件對選取的防護網系統進行了驗證。得到以下結論。

(1)滾石斜拋射運動階段能量變化呈現拋物線型，碰撞階段法向恢復系數與碰撞前的速度成反比，滾動滑動階段滾石動能與速度位移均成線性正比關系。

(2)碰撞斜拋與滾動相比較，滾動階段造成的能量損耗更大，坡度與斜坡材料對滾石的運動狀態具有很大的影響，與45°斜坡相比較，兩緩一陡，兩陡一緩斜坡對滾石的能量損耗更大，清潔基巖材料覆蓋的斜坡對滾石的能量損耗影響最低，通過鋪設土壤和植被能有效降低滾石的能量，減輕滾石災害破壞。

(3)通過Rocfall軟件可獲取滾石運動參數，速度、能量、彈跳高度用于防護裝置的位置布置及選型設計如被動防護網裝置。

(4)利用ANSYS/LS-DYNA可進行被動防護裝置選型設計降低防護成本，驗證選型合理性，通過不斷調整被動防護網構件參數來進行優化設計，通過適當選取R7(7圈環繞)/3 mm/300 mm，并通過仿真分析結果表明設計選取的網片合理對滾石能有效攔截。