深海采礦揚礦管的縱向振動分析

肖林京， 左 帥， 于志豪

(山東科技大學機械電子工程學院，青島 266590)

位于國家管轄海域以外的國際海底區域蘊藏著大量的錳結核[1]。人們利用深海采礦技術，將錳結核從海洋下提取出來。經研究發現，選擇管道提升式采礦系統適用于現代化的商業開采[2]。揚礦管在復雜的海洋環境中，在各種力的作用下會使揚礦管產生變形和應力，從而容易引起揚礦管的疲勞破壞和失效，導致使用壽命縮短，嚴重時還會導致重大的安全事故[3]。因此，對揚礦管縱向振動的研究具有重要的意義。

前人對揚礦系統各部分的子系統進行了研究，并在云南省撫仙湖進行了135 m湖上試驗，驗證了深海采礦系統的可行性[4]。韓國海洋科學技術院研發了一套KIOST采礦系統，并別在淺水區域和深水區域進行了路徑跟蹤試驗，然后與2015年進行了500 m水深泵和中間礦倉的相關采礦實驗[5]。

在理論研究方面，Cui等[6]研究了揚礦管的構型對揚礦管振動和軸向應力的影響；邱顯焱[3]對揚礦管的縱向振動進行分析，并采用附加單個吸振器的方法抑制縱向振動；馮雅麗等[7]利用有限元的方法對揚礦管進行了靜力分析和動態分析，采用ADINA軟件分析了在海水中不同海浪周期下揚礦管的振動特性；梁彬等[8]利用ABAQUS軟件進行仿真分析，得到了揚礦管的軸向凈身長量，并得到了振動隨位置變化的結果。目前，對揚礦管研究主要利用靜力學理論對軸向應力和軸向應變進行分析，對于揚礦管的縱向振動分析，忽略了阻尼對固有頻率、振動幅值及軸向應力的影響。為此，建立揚礦管的縱向振動微分方程，分別分析在有阻尼系統響應與無阻尼系統響應兩種下揚礦管的固有頻率、不同點上振幅隨時間的變化曲線以及揚礦管頂端軸向應力隨時間變化關系。以期為后續對管道穩定性的研究和減振工作提供理論基礎。

1 建立揚礦管動力學模型

深海采礦系統的原理圖如圖1所示，具體工作方式：集礦機(圖2)采集多金屬結核并進行脫泥和破碎，經軟管輸送到中間礦倉(圖3)，再通過泵組經揚礦管輸送到采礦船上。

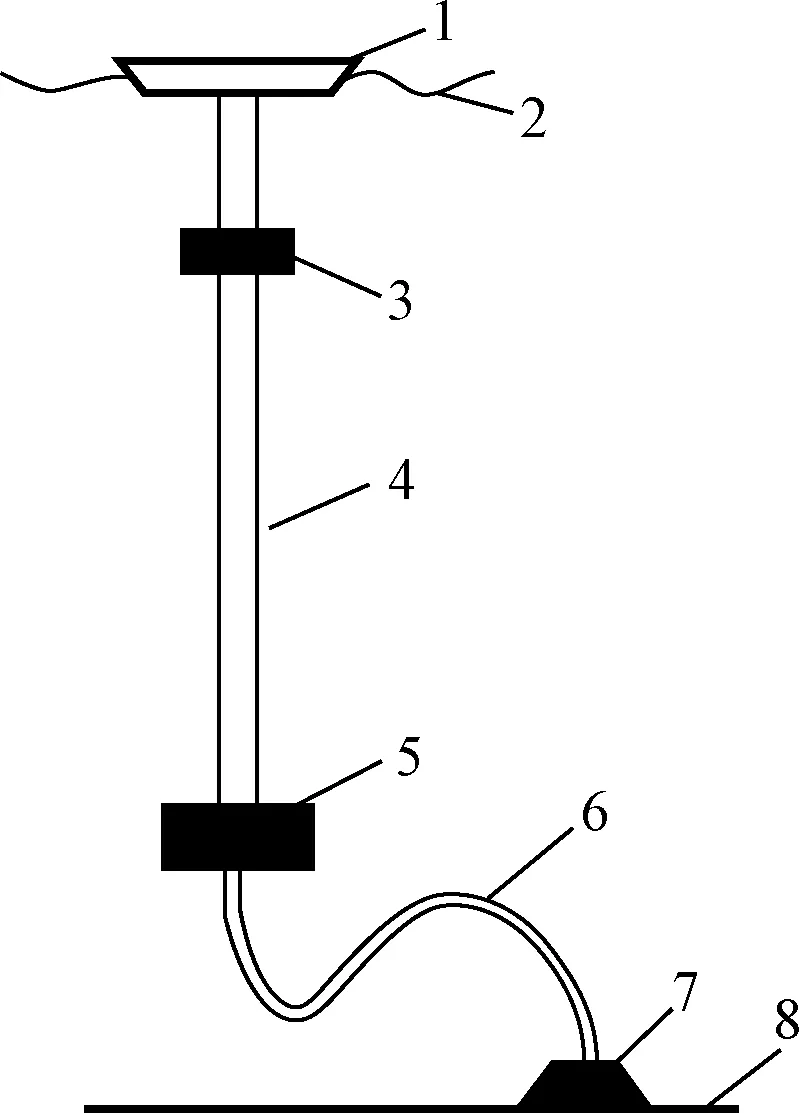
1為采礦船;2為海洋表面;3為泵組;4為揚礦硬管;5為中間礦倉;6為軟管;7為集礦機;8為海床圖1 深海采礦系統Fig.1 Mining system in the deep sea

圖2 中國開展湖試試驗中的集礦機Fig.2 China trialed miner in a lake

圖3 韓國開展海試試驗中的中間礦倉Fig.3 Korea piloted buffer in the sea

揚礦管的總長度為l，上端與采礦船為鉸接連接。即揚礦管頂端的運動與采礦船的運動方式相同。揚礦管的末端與軟管連接，由于軟管的質量和剛度比揚礦管小，因此假設軟管不影響揚礦管的振動，末端視為自由端，進一步假設，中間礦倉視為集中質量，現將揚礦管簡化為一維振動問題，不考慮揚礦管的偏移、彎矩與扭矩。

揚礦管由無限多質點組成，因此每一截面的位移均不同，揚礦管任意截面x的位移u是關于位置x和時間t的函數，記為u(x,t)。

基于振動力學理論[9]建立揚礦管的縱向振動的偏微分方程[10]。

(1)

式(1)中:A為橫截面面積；E為剛度系數。

m(x)=m0+m1δ(x-l)

(2)

式(2)中：δ(x)為狄拉克函數；m0為揚礦管的單位長度質量；m1為中間礦倉集中質量。

c(x)=c0+c1δ(x-l)

(3)

式(3)中：c0為揚礦管單位長度阻尼系數；c1為中間礦倉阻尼系數。

為了求解式(1)，需要確定揚礦管的邊界條件與初始條件。分析可知，揚礦管的邊界條件為上端鉸接，下端自由，可以寫為

(4)

式(4)中：u0(t)為采礦船的運動，采礦船隨著海浪做升沉運動可以看作簡諧運動，其簡諧運動方程為

u0(t)=rsin(ω0t)

(5)

式(5)中：r為采礦船升沉運動幅值；ω0為運動周期。

揚礦管與采礦船鉸接，為采礦船所受到的運動方程。為了求解揚礦管的絕對位移響應u(x,t)，可以先求出揚礦管相對于采礦船的相對位移u1(x,t)，在通過合成的方法得到u(x,t)，表達為

u(x,t)=u1(x,t)+u0(t)

(6)

將式(6)代入揚礦管的縱向振動方程[式(1)]得:

(7)

將式(6)代入揚礦管的邊界條件[式(4)]得到揚礦管相對位移的邊界條件:

(8)

2 理論分析

2.1 振型函數的分析

揚礦管的縱向振動方程屬于波動方程，其求解方法可以用分離變量法來得到，即

u1(x,t)=φ(x)q(t)

(9)

式(9)中：φ(x)為振型函數，是僅與坐標x有關的待定函數；q(t)為時間函數，是僅與時間有關的待定函數，振型函數[11]的通解為

(10)

分別對揚礦管的無阻尼系統響應時的固有頻率和有阻尼系統響應時的固有頻率進行求解，求解結果如表1所示。

表1 兩種情況下固有頻率及阻尼比Table 1 Natural frequencies in two conditions and damping ratios

在結合歸一化條件，可以求得揚礦管的振型函數為

(11)

采用MATLAB對揚礦管的前5階振型函數進行繪制，結果如圖4所示。

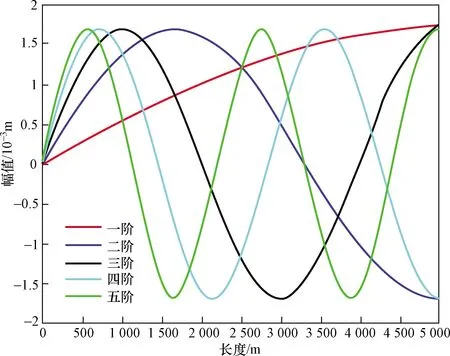
圖4 揚礦管的前5階正則振型函數曲線Fig.4 The first five phases of the regular vibration mode function

2.2 揚礦管振動響應函數的分析

在2.1節已得到揚礦管前5階的固有頻率與相應的振型函數，利用振動型疊加原理對揚礦管的相對位移進行求解，可假設為

(12)

式(12)中：φi(x)為相應于固有頻率ωni的主振型；ηi(t)為第i個正則坐標下的響應。將式(12)代入式(7)中得到

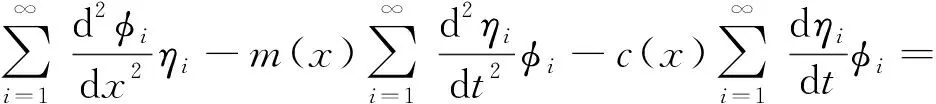
(13)

兩邊同時乘以φj(x)，并沿揚礦管的長度進行積分，得到:

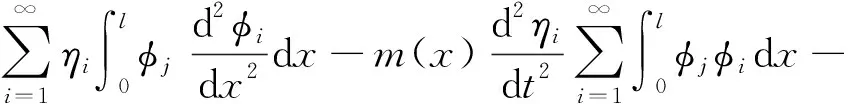
(14)

式(14)中：φi(x)為相應于固有頻率ωnj的主振型。

根據正交條件，得到:

(15)

式(15)中:ηj(t)為第j個正則坐標下的響應；ξj為阻尼比，j=1,2,…,n；ωnj為揚礦管的第j階固有頻率，j=1,2,…,n。

(16)

式(17)利用Duhamel積分得到ηj的解:

ηj(t)=ηj(t0)e-ξjωnjtcos(ωdt)+

(17)

式(17)中：ξj為阻尼比;ωd為揚礦系統有阻尼時的固有頻率。前5階阻尼比及揚礦管有阻尼時的前5階固有頻率如表1所示。

根據初始條件:

(18)

將式(11)、式(17)代入式(12)中，再將式(12)、式(5)代入式(6)中，最終可以得到揚礦管隨縱向振動方程的解析解。

由揚礦管的響應解可以看出，揚礦管的高階響應要比揚礦管的低階響應小，因此計算前5階響應就可以得到精度較高的結果。

2.3 軸向應力分析

對揚礦系統產生的軸向應力進行分析，其表達式可用式(19)表示。

(19)

式(19)中：Wb為中間礦倉的質量；W0為揚礦管單位長度的質量。

3 仿真分析

利用揚礦管的邊界條件最終得到揚礦管的固有頻率和有阻尼系統的固有頻率，表1為MATLAB[12]計算結果。

利用莫爾在1968、1970年發表的模型試驗資料[3]來估的升沉運動幅值，根據莫爾經驗公式可得三一垂蕩幅值，可以求得r。在六級風況下，采礦船的幅值r=4 m，周期T=10 s[1]。

根據上述計算原則，參考文獻[1]中所采用的相關數據，揚礦管的設計參數如表2所示。

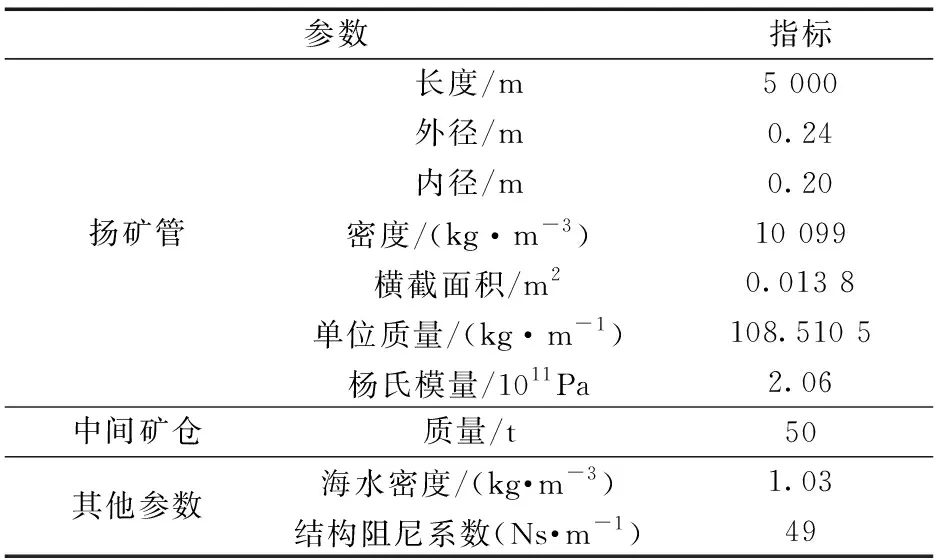
表2 揚礦子系統的主要物理參數Table 2 Main physical parameters of the lifting pipe

3.1 無阻尼系統響應時揚礦管的分析

對取樣點進行仿真，在不考慮阻尼系統響應的情況下，分別取揚礦管距海平面的1 000、3 000、5 000 m處，研究位移隨時間的變化關系。

通過圖5可知，在無阻尼系統響應時，從0～1 000 m時振幅變化的最快，3 000 m后的幅值變化較小。在1 000 m內，由于揚礦管相對位移的影響較小，運動規律類似于簡諧運動，但隨著深度的增加，揚礦管的相對位移振幅的增加。絕對位移變大，在達到峰值的時刻出現許多尖點，容易對揚礦管產生破壞。

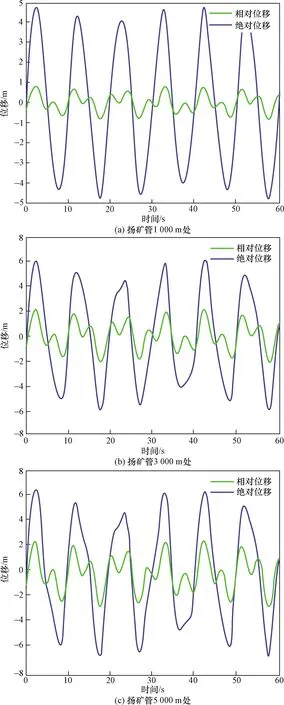
圖5 揚礦管1 000、3 000、5 000 m處位移隨時間的變化規律(無阻尼)Fig.5 The displacement variation rule of the lifting pipe at 1 000、3 000、5 000 m below sea level with time varying(without damping)

3.2 有阻尼系統響應時揚礦管的分析

在考慮阻尼系統響應的情況下，同樣分別取揚礦管距海平面的1 000、3 000、5 000 m處，研究位移隨時間的變化關系。

由圖6可知，振幅的變化趨勢與無阻尼時的振幅變化趨勢基本相同。但由于海水阻尼的影響，揚礦管上各點的幅值先減小，后保持穩定的狀態。還可以發現，當達到穩態時，揚礦管上任何位置的最大幅值基本穩定5.34 m左右，其運動規律類似于簡諧運動。

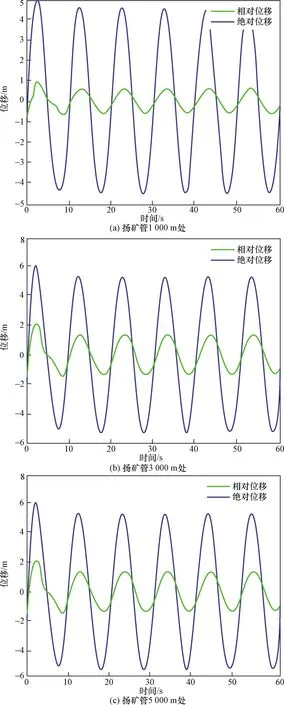
圖6 揚礦管1 000、3 000、5 000 m處位移隨時間的變化規律(有阻尼)Fig.6 The displacement variation rule of the lifting pipe at 1 000、3 000、5 000 m below sea level with time varying(with damping)

3.3 揚礦管的軸向應力分析

揚礦管所受的軸向應力是影響揚礦管變形的重要因素。下面取揚礦管最頂端的位置，研究軸向應力隨時間變化的關系，結果如圖7所示。

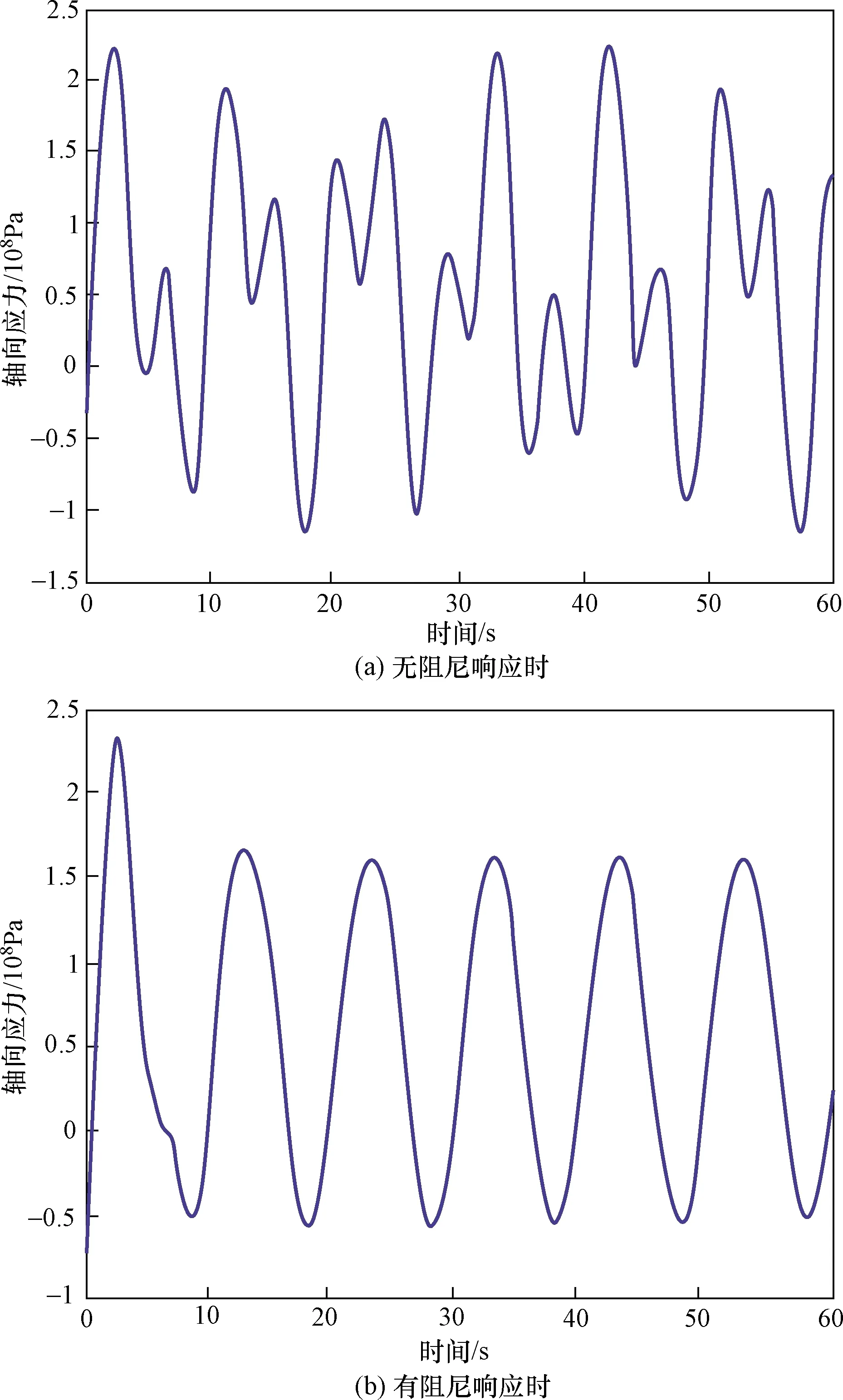
圖7 有無阻尼響應時揚礦管頂端軸向應力隨時間變化Fig.7 With and without any damp system responses,axial stress,at the top of the lifting pipe,changes with time

由圖7可以看出，當達到穩態時，在有阻尼系統響應要比無阻尼系統更加穩定。且有阻尼系統響應時揚礦管頂端的最大軸向應力要比無阻尼系統響應時的最大軸向應力小25.5%。

在以上兩種情況下，在前10 s揚礦管頂端軸向力的變化規律都是先增加后減小，選定前10 s，繪制揚礦管軸向應力隨揚礦管位置的變化關系。

由圖8可以看出，在大部分時刻，揚礦管的軸向應力隨著管長的增加而減小，在個別的時刻會先增大，從1 000 m后在減小。因此，在大部分時刻，揚礦管所受到最大軸向力出現在最頂端。

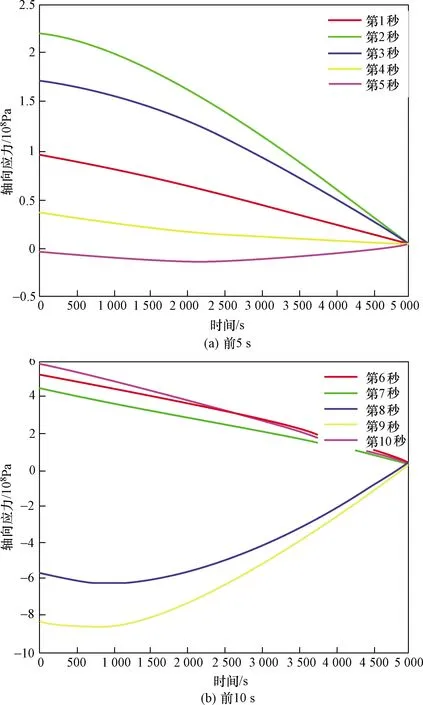
圖8 前10 s軸向應力隨位置的變化曲線Fig.8 Axial stress changes with water depth for the 10 s

4 結論

研究了深海采礦揚礦管的縱向振動，建立了揚礦管的縱向振動偏微分方程，求解了揚礦管的振型函數以及響應函數，采用振型疊加法求解了揚礦管的縱向振動公式，并對揚礦管的軸向應力進行分析，得到了如下結論。

(1)在有阻尼系統響應和無阻尼系統響應兩種情況下，隨著水深的增加，揚礦管上個點的幅值先增大，后逐漸趨于穩定狀態。在揚礦管的最末端，前一種情況的最大幅值要比后一種減少1.101 m。

(2)當達到穩態時，有阻尼系統響應條件下的軸向應力的最大值為2.19×108Pa，無阻尼系統響應條件下的軸向應力最大值為1.63×108Pa，減少幅度約為25.5%，且大部分時刻軸向力隨著管長增加而減少，少數時刻隨著管長的增加，軸向力先增大后減小。

(3)當考慮海水的阻尼時，揚礦管不同點處位移隨時間運動規律及軸向應力隨時間的變化關系更加規則。因此，海水阻尼可以減少揚礦管突然受到的沖擊，使得揚礦管的運動類似簡諧運動。

(4)由以上結論可知，揚礦管的最大振幅發生在最下端，在大部分時刻，揚礦管最頂端的軸向應力最大。為此，該研究可以為下一步的減振研究與穩定性研究提供理論依據。在進行減振研究時，可主要在管道的最頂端與最低端展開減振研究工作。