基于單值中智VIKOR法的供應商優選模型

劉 慶， 化小會

(1.新鄉學院數學與統計學院, 新鄉 453003； 2.河南師范大學數學與信息科學學院, 新鄉 453007)

隨著經濟全球化的不斷深入,供應鏈管理(SCM)已經成為在高度競爭的全球經濟中提高企業國際競爭力的一個重要因素。在SCM信息系統中關鍵的問題之一是供應商選擇,根據成本、服務、風險等準則,從備選方案中尋找最佳供應商,這是一個復雜的多屬性決策(multi-attribute decision making, MADM)問題。近年來，很多學者[1-4]提出了供應商選擇的MADM方法類型,但是這些方法都是假設屬性信息精確已知,且可以準確評估。然而,因為評估對象的復雜性不斷增加,使得決策者在選擇過程中很難準確地評估關于其屬性的偏好信息。因此,在實際的MADM問題中往往會出現不精確和不確定的評價。在這種情況下,如何有效地處理不確定性或不完整性的信息,已經成為MADM分析中的一個關鍵問題。目前描述不確定性信息最完備的工具是Smarandache[5]提出的中智集(neutrosophic sets, NS),它具有獨立的真值隸屬度、不確定隸屬度和謬誤隸屬度,所以可以更準確的描述不完整、不精確、不一致等模糊信息,是對模糊集[6]、直覺模糊集[7]和區間值直覺模糊集[8]概念的一種擴展。但是NS是從哲學觀點提出的概念,盡管可以完備的描述性不確定信息,然而一個重要特性是定義在標準或非標準的單位子區間,在實際的工程和科學計算上應用不方便,為了解決這個問題,Wang等[9]引入單值中智集(single-value neutrosophic sets, SVNS),它是NS的子類,其特征是真值隸屬度、不確定性隸屬度和謬誤隸屬度定義在標準的單位子區間,可以很方便地應用于實際。近年來,NS與經典的TOPSIS法[10]相結合,在多屬性決策問題方面應用很廣泛[11-14]。

VIKOR法是Opricovic[15]在1998年首次提出的,它是一種基于理想解的折中排序方法,通過最大化群體效用和最小化個體遺憾來實現有限備選決策方案的最優排序。它的基本思想是先確定正理想解和負理想解,然后根據每個備選方案的取值,選擇最接近理想解的方案。雖然VIKOR法與經典TOPSIS方法相似,但Opricovic通過比較兩種方法,指出TOPSIS的最優解不一定是最接近理想點解的[16],但是VIKOR法可以克服這種現象。

文獻[17]對擴展的VIKOR法與超序方法進行了比較,文獻[18]提出了一種基于模糊集理論和VIKOR法的MADM模型來處理供應鏈系統中的供應商選擇問題,文獻[19]提出了一種擴展的VIKOR方和TOPSIS法的來解決模糊集信息不確定的MADM問題,文獻[20]提出了一種基于VIKOR的猶豫模糊多準則決策方法,但是在單值中智環境下的VIKOR法尚鮮見報道。

為解決上述問題，將VIKOR法推廣到單值中智集(NS)環境下,并且用它處理供應商選擇問題。首先回顧中智集的相關概念和運算,提出了廣義的單值中智集距離,并且給出單值中智環境下的加權平均集結算子；給出VIKOR法的基本思想和處理過程；把VIKOR法推廣到單值中智環境下,建立基于單值中智VIKOR法的供應商優選模型；通過一個供應商選擇的實例,驗證提出模型的有效性和實用性,并進行靈敏度分析,展示決策機制系數的不同取值對備選方案排序的影響,驗證模型的靈活性。

1 預備知識

1.1 中智集及單值中智集

定義1設X是一個點(對象)空間,它的任意一個元素用x表示,X上的一個中智集A用一個真值隸屬度函數TA(x)、不確定隸屬度函數IA(x)和謬誤隸屬度函數FA(x)來表示,這里TA(x)、IA(x)、FA(x)是]0-,1+[的標準或非標準實數子集[4],即

(1)

且滿足0-≤supTA(x)+supIA(x)+supFA(x)≤3+。

需要說明的是非標準有限數1+=1+ε與0-=0-ε中,1和0是標準部分,無窮小數ε>0是非標準部分,稱]0-,1+[為非標準的單位子區間,一般來說,其左右邊界是模糊的。另外,不確定隸屬度函數IA(x)不僅能表示不確定,還可以表示不可靠、不一致、不明確、未知等模糊信息,這就使得處理不確定信息的能力進一步加強。但是在中智集的定義中,隸屬度取值于]0-,1+[的標準或非標準的單位子區間,因其邊界的模糊性,在科學計算中是非常不方便的,為此學者Wang等[9]改進了中智集的定義,提出了單值中智集,可以方便地應用于工程和科學中。接下來給出一些關于單值中智集的基本定義和運算。

定義2設X是一個給定的論域,X上的一個單值中智集A可以由真值隸屬度函數TA(x),不確定隸屬度函數IA(x)和謬誤隸屬度函數FA(x)[9]表示為

A={[x,TA(x),IA(x),FA(x)]x∈X}

(2)

式(2)中：TA(x)：X→[0,1],IA(x)：X→[0,1],FA(x)：X→[0,1]。對?x∈X,有0≤TA(x)+IA(x)+FA(x)≤3。

論域X上的單值中智集A中的元素,稱為單值中值數SN，記為[TA,IA,FA]。論域X上全體單值中智集的集合記為SS。

設A為定義在論域X上的一個SS,當X連續時,A可表示為

(3)

當X離散時,A可表示為

(4)

1.2 單值中智集的相關運算

中智集和單值中智集作為模糊集、直覺模糊集的推廣,有三個隸屬度,也有不同于FS和IFS的運算和性質,文獻[9,21-22]給出單值中智集的相關運算和性質。

定義3設A和B是論域X上的兩個SS,則對?x∈X,定義如下。

(1)A是B的子集,即：A?B?TA(x)≤TB(x),IA(x)≥IB(x),FA(x)≥FB(x)。

(2)A和B滿足A=B?A?B且B?A。

(3)A的補集記作Ac,且滿足TAc(x)=FA(x),IAc(x)=1-IA(x),FAc(x)=TA(x)。

(4)A∪B={max(TA(x),TB(x)],min[IA(x),IB(x)],min[FA(x),FB(x)]}

A∩B={min(TA(x),TB(x)],max[IA(x),IB(x)],max[FA(x),FB(x)]}

定義4設A和B是論域X上的兩個SVNS,則對?x∈X,?λ∈R且λ>0,有:

(1)和運算：A⊕B=[TA(x)+TB(x)-TA(x)TB(x),IA(x)IB(x),FA(x)FB(x)]。

(2)積運算：A?B=[TA(x)TB(x),IA(x)+IB(x)-IA(x)IB(x),FA(x)+FB(x)-FA(x)FB(x)]。

(3)數乘運算：λA={1-[1-TA(x)λ)],IA(x)λ,FA(x)λ}。

定義5設A1,A2,…,An是論域X上的n個單值中智數,記Aj=[TAj,IAj,FAj]的權重為wj(j=1,2,…,n),單值中智集的加權平均集結算子定義為

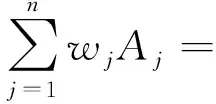
(5)

1.3 兩個單值中智集的距離

文獻[21]研究了單值中智集的距離、相似度量和熵,接下來推廣單值中智集的距離概念,給出廣義的單值中智集的距離公式。

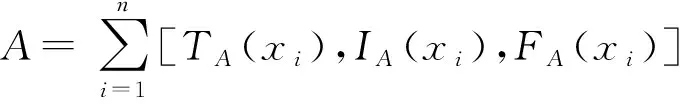
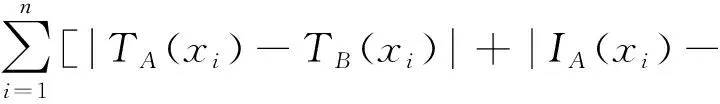
IB(xi)+FA(xi)-FB(xi)]/3n,i=1,2,…,n

(6)

其標準化的Euclidean距離為

(7)

這里的Hamming距離和Euclidean距離都考慮了真值隸屬度、不確定隸屬度、謬誤隸屬度,在此基礎上推廣兩個SVNSs的距離公式,給出兩個Ss廣義的距離公式。

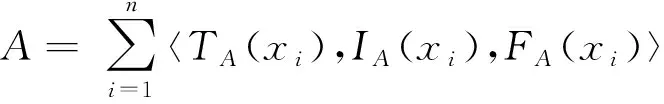
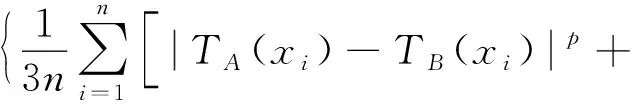
IA(xi)-IB(xi)p+FA(xi)-

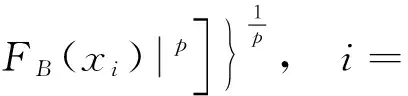
(8)

如果取p=1,式(8)就退化為定義6中Ss的標準化Hamming距離公式[式(5)];如果取p=2,式(8)就退化為定義6中Ss的標準化的Euclidean距離公式[式(7)]。

2 經典VIKOR法

VIKOR法是學者Opricovic于1998年首次提出的一種處理MADM問題的最佳優化妥協方法,側重于從一組備選方案中進行排序和選擇,并針對屬性沖突的問題確定折中的解決方案,給出一個或者多個折中的方案,從而做出最終決策。考慮具有m個備選方案Ai(i=1,2,…,m)和n個屬性Cj(j=1,2,…,n)的MADM問題,有t位決策專家進行評價,從備選方案中選出最優決策方案。經典VIKOR法的處理步驟如下：

步驟1構造m行n列的決策矩陣D=[aij]m×n。

步驟2確定每個屬性對應的權重wj(j=1,2,…,n)。

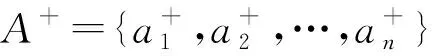
步驟4計算群體效用值Si和個體遺憾值Ri：

(9)

(10)

式中：Si為第i個備選方案的群體效用值,Ri為第i個備選方案的個體遺憾值。

步驟5計算各備選方案的利益比率(又稱折中評價值)Qi:

Qi=v(Si-S*)/(S--S*)+(1-v)(Ri-R*)/(R--R*)

(11)

式(11)中：S*=miniSi；S-=maxiSi；R*=miniRi；R-=maxiRi；v∈[0,1]相當于一個權重,稱為決策機制系數或最大群體效用權重。

步驟6對Si、Ri和Qi進行排序并確定最終方案。

3 基于單值中智VIKOR法的供應商優選模型

供應商選擇是供應鏈管理中的一個重要問題,本質上是一個多準則決策問題,供應商的選擇高度依賴于專家的評估。在這一過程中,由于人的主觀判斷能力的不足,不可避免地涉及各種類型的不完整、不全面、不精確、不一致等模糊信息等,現有的方法無法充分處理這些類型的不確定性,然而單值中智集有三個隸屬度,可以較好地描述模糊信息,接下來把VIKOR法推廣到單值中智環境下來處理,建立基于單值中智VIKOR法的供應商優選模型。

3.1 MADM問題的語言變量

供應商選擇問題本質上是一個MADM問題,在MADM問題中,對決策專家和屬性的評價一般都采用語言變量給出,它是一種變量,其值用描述性的語言表示,而不是以數字為特征。比如,可以用非常重要、重要、中等、不重要、非常不重要等語言術語來描述對專家和屬性的評價。在實際中,為了保證評價的中間值接近0.5,其他值比較對稱。語言術語的數量一般都取奇數,如常見的5級、7級、9級、11級語言變量。在模糊集環境、直覺模糊集環境以及Vague集環境下很多學者都給出了語言術語對應的模糊數、直覺模糊數以及Vague值的對應關系。

從定義3和文獻[21]可知,單值中智數〈TA,IA,FA〉的最大值是〈1,0,0〉,最小值是〈1,0,0〉,單值中智數的大小要考慮真值隸屬度TA、不確定隸屬度IA和謬誤隸屬度FA,評價越好,則真值隸屬度TA越大,不確定隸屬度IA和謬誤隸屬度FA越小。反之真值隸屬度TA越小,不確定隸屬度IA和謬誤隸屬度FA越大,接下來給出單值中智環境下的語言術語及其對應的單值中智數,如表1所示。

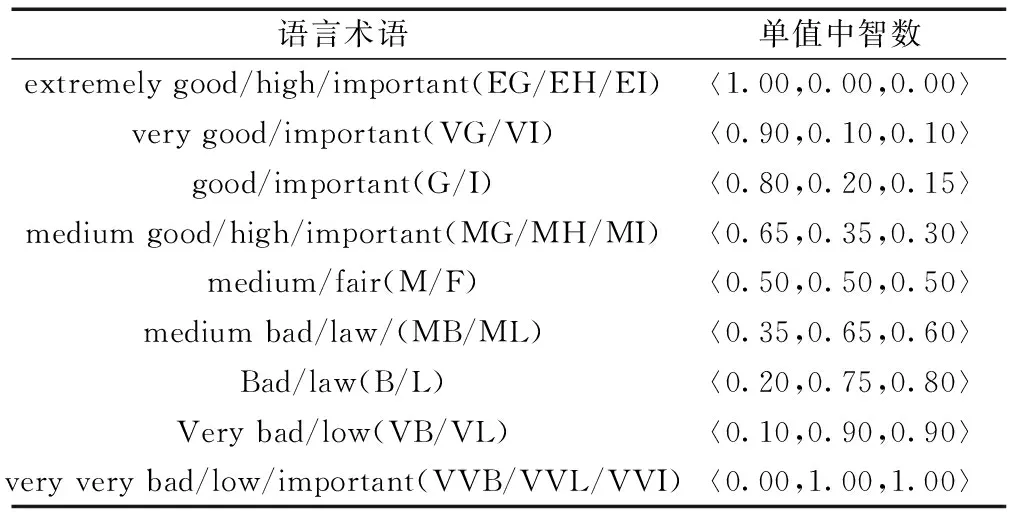
表1 用SN對決策專家和屬性進行評級的語言術語Table 1 Linguistic terms for rating of decision makers and attribute index with SN

3.2 基于單值中智VIKOR法的供應商優選模型

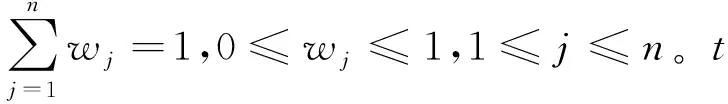
步驟1確定每位決策專家的權重。

首先確定各位決策專家的重要程度,根據表1確定每位決策專家評級的單值中智數,假設第k位決策專家對應的單值中智數是Ek=〈Tk,Ik,Fk〉,則根據文獻[21],第k位決策專家的權重為

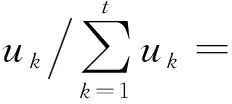
(12)

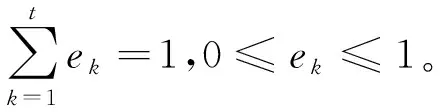
步驟2確定屬性指標的權重。

確定出各位決策專家的權重以后,每位決策專家要通過語言變量對m家備選供應商Ai(i=1,2,…,m)的n個屬性進行評價,并給出對應的單值中智數,組成m行n列的屬性指標評價矩陣。對模糊信息不確定程度度量的常用方法是熵權法[5-6],因為語言變量的不確定性,需要用熵權法確定n個屬性指標的權重,這里給出單值中智集的熵權法來確定屬性權重。

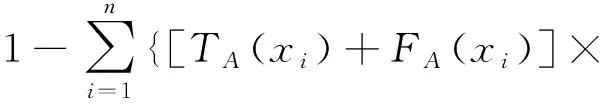
IA(xi)-IAc(xi)}/n

(13)

在對m家供應商的n個屬性進行評價的過程中,每位決策專家給出的不同屬性所起作用重要程度也是不一樣的,如果屬性Cj可以用單值中智數Aj表示,則每個屬性指標的權重wj計算方法如式(14)所示：

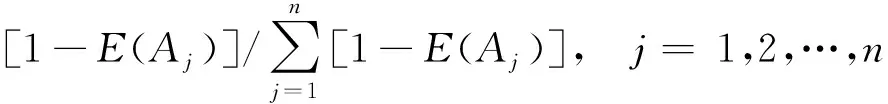
(14)

從而到屬性指標的權重向量w=(w1,w2,…,wn)。

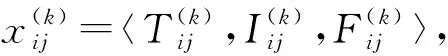
(15)

步驟4集結所有的單值中智決策矩陣D(k),構建綜合中智決策矩陣D。

利用定義5中給出的式(4),對所有單值中智矩陣與每位決策專家的權重ek進行集結,構建綜合中智決策矩陣如下：

(16)

步驟5確定單值中智數的正理想方案A+和負理想方案A-。

(17)

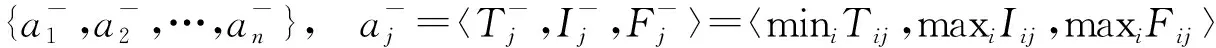
(18)

式中：i=1,2,…,m；j=1,2,…,n。

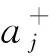
步驟6分別計算單值中智環境下每家供應商的群體效用值Si和個體遺憾值Ri：

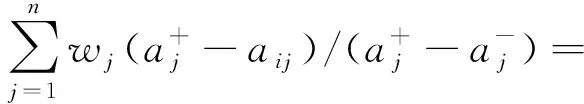
(19)

(20)

式中：wj為步驟2中得到的屬性指標Cj權重,j=1,2,…,n。

步驟7綜合考慮最大化群體效用同時最小化個體遺憾,計算各家供應商的折中評價值Qi：

Qi=v(Si-S*)/(S--S*)+(1-v)(Ri-R*)/

(R--R*)

(21)

式(21)中：S*=miniSi；S-=maxiSi；R*=miniRi；R-=maxiRi；決策機制系數v∈[0,1],相當于一個權重，稱為決策機制系數或最大群體效用權重,用來權衡Si和Ri之間的比例。v的不同，說明了考慮側重點的不同,調節v的取值,可以綜合調節最大群體效用和最小個體遺憾,得到的排序方式更符合實際。若v>0.5,則表示根據最大化群體效用進行評價；若v<0.5,則表示根據某一屬性指標或者說是最小化個體遺憾進行決策；若v=0.5,則表示根據折中均衡的方式進行決策,也就是考慮全部屬性指標的同時又照顧某一屬性指標的影響。

步驟8對Si、Ri和Qi按照升序排序并確定最佳供應商。

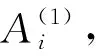
準則1優勢準則。

(22)

4 實例分析

4.1 基于單值中智VIKOR法的供應商優選模型算例分析

近年來,全球經濟發展和公共衛生受到碳排放增加的威脅,這促使世界各地的企業和政府試圖刺激和增加對低碳和綠色經濟的投資。在這個決策過程中,一個關鍵階段是在低碳供應鏈中選擇合適的綠色供應商。這個過程涉及不確定信息的各種因素,所有這些因素都必須同時考慮和評估。因此,綠色供應商選擇是一個非常復雜的模糊決策過程。低碳供應鏈管理領域的3位決策專家被邀請來評估和選擇一家低碳供應商,從4家潛在供應商Ai(i=1,2,3,4)中按照低碳技術C1、成本C2、風險因素C3、和能力C4等4個屬性對供應商進行評估,選出最佳供應商。3位決策專家Dt(t=1,2,3)的集合記為D={D1,D2,D3},4家潛在的供應商Ai(i=1,2,3,4)組成備選方案集A={A1,A2,A3,A4},4個屬性Cj(j=1,2,3,4)組成屬性集C={C1,C2,C3,C4},利用前面建立的單值中智VIKOR法的供應商優選模型,找出最佳的供應商。

步驟1確定每位決策專家的權重。根據決策專家的能力和水平,用語言變量對3名決策專家進行評價,通過表1確定對應的單值中智數,如表2所示。

表2 決策專家重要程度的SN表示Table 2 Importance of decision makers expressed with SN

然后通過式(11)和表2,計算出3位決策專家的權重向量e=0.378,0.342,0.280。

步驟2確定屬性指標的權重。3名決策專家利用表1給出的語言術語分別對低碳技術(C1)、成本(C2)、風險因素(C3)、和能力(C4)等4個屬性進行評級,評估的結果如表3所示。

表3 3名決策專家對屬性權重的評估Table 3 Assessments of attribute weights given by four decision makers

利用式(12)、式(13)、表3可以求出各屬性的權重向量w=(0.339,0.121,0.306,0.234)

步驟3每個決策專家給出單值中智決策矩陣。3位決策專家Dk(k=1,2,3)對4家潛在供應商Ai(i=1,2,3,4)的4個屬性Cj(j=1,2,3,4)通過表1給出的語言變量進行評價,得到表4。

表4 3名決策專家對4家供應商的語言評價信息Table 4 Evaluation information of four suppliers by three decision experts

根據表4,可以得到3名決策專家的單值中智決策矩陣D(k)(k=1,2,3)，如式(23)～式(25)所示:

(23)

(24)

(25)

步驟4集結3組單值中智決策矩陣D(k),構建綜合中智決策矩陣D。

利用定義5給出的單值中智加權平均集結算子公式[式(4)],把3組單值中智決策矩陣D(1)、D(2)、D(3)與專家權重e=(0.388,0.342,0.280)進行集結,構建綜合中智決策矩陣如式(26)所示：

(26)

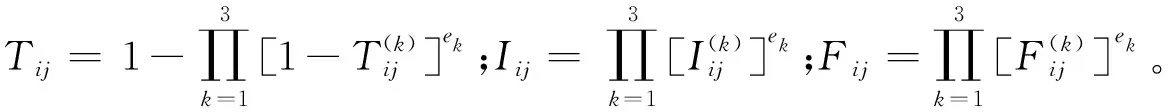
步驟5確定單值中智數的正理想方案A+和負理想方案A-根據式(17)、式(18)和綜合單值中智決策矩陣,可得：

(27)

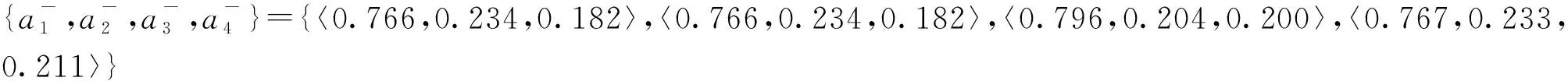
(28)

步驟6分別計算單值中智環境下每家供應商的群體效用值Si和個體遺憾值Ri。

由廣義的單值中智集距離公式[式(8)]、式(20)、式(21)可以計算4家供應商的群體效用值Si和個體遺憾值Ri。距離公式采用定義7中的式(8),可以驗證p的取值不影響排序的順序,這里為了運算簡便,取p=2。如表5所示。

步驟7綜合考慮最大化群體效用同時最小化個體遺憾,計算各家供應商的折中評價值Qi。

由式(18)～式(20)求出各家供應商的折中評價值Qi,在本例的單值中智VIKOR法中,選取v=0.5,意味著以決策專家協商達成共識的折中方式選擇最佳供應商。計算結果如表5所示。

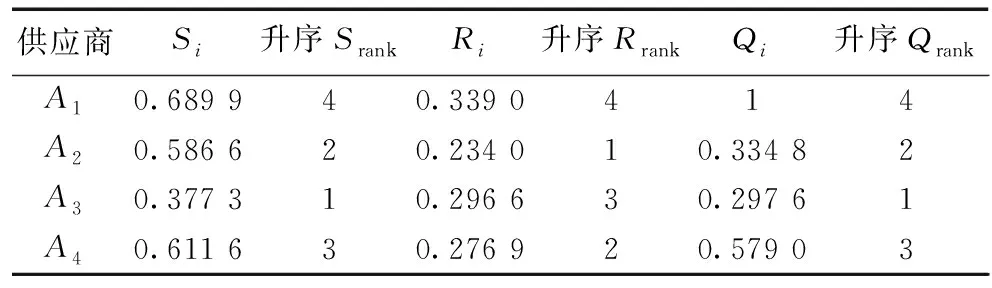
表5 4家供應商的Si、Ri和QiTable 5 The Si,Ri and Qi of the four suppliers

步驟8對Si、Ri和Qi分別按照升序排列并確定最佳供應商。

根據Si、Ri和Qi的數值大小對備選供應商進行升序排列,得到3組排序序列Srank、Rrank和Qrank,如表5所示。根據折中評價值Qi的排序得到備選供應商優先順序為A3>A2>A4>A1,可得最佳供應商為A3。下面驗證是否滿足兩個可接受準則。

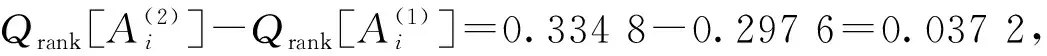
準則2穩定性準則。因為A3在Srank排名也是第1,說明滿足穩定性準則。

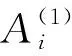
需要說明的是Qi的最大值為1,說明群體和個體都認為A1最弱供應商。

4.2 靈敏度測試

在前面的單值中智VKIOR法實例計算中,對決策機制系數v的取值按照折中辦法取0.5,很多情況下,v的取值不同,折中方案的排序也不同,特別是優勢準則不滿足的情況下,不同的決策機制系數將會對應不同的優選方案。接下來通過對決策機制系數v設置不同的取值進行靈敏度測試(每間隔0.1取一個值),如圖1、圖2所示。

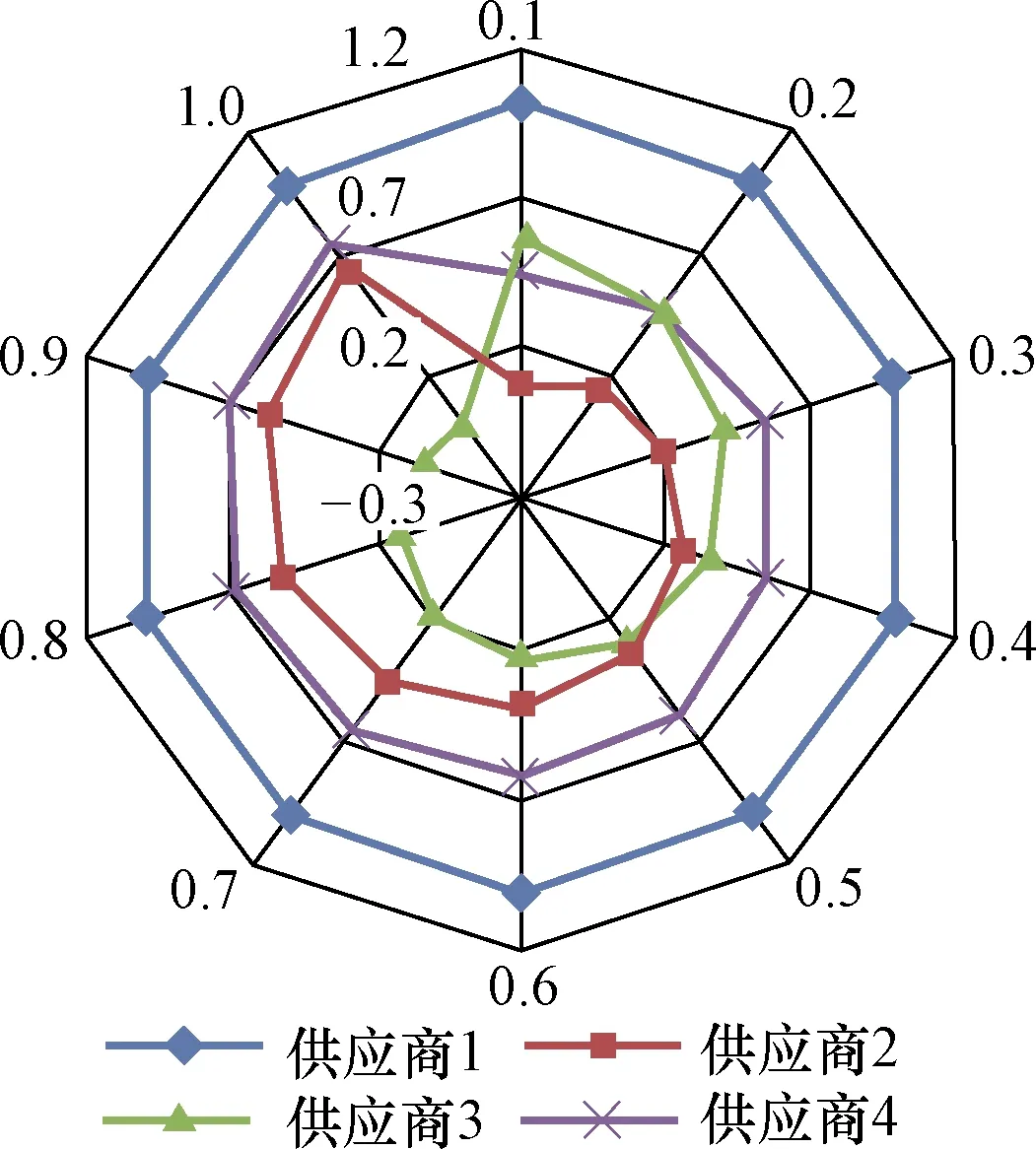
圖1 供應商折中評價值Qi變化情況Fig.1 Changes in supplier’s tradeoff valuation Qi

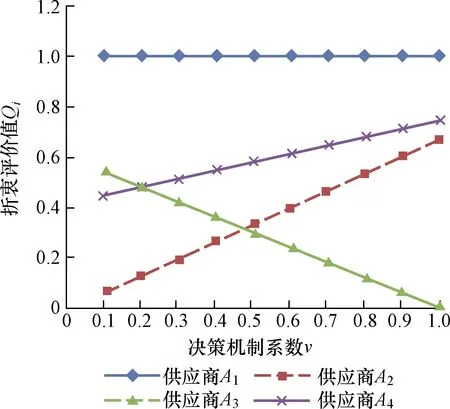
圖2 供應商Ai排序變化情況Fig.2 Changes in supplier ranking

從圖1、圖2可以看出,當v≤0.47時A2為最佳供應商,v>0.47時,A3為最佳供應商,一直保持穩定并且滿足可接受準則2,隨著決策機制系數v逐步靠近最大值1,A3性能越來越好,優勢性越來越明顯。測試結果表明,排序結果對決策機制系數(最大群體效用權重)v的變化具有敏感性,同時在某個范圍內也具有一定的穩定性。進一步說明了建立的模型具有靈活性、實用性、有效性。在實際的決策過程中,如果重視最大化群體效用同時兼顧最小化個體遺憾,決策機制系數就在0.5附近取值,如果對某一個體考慮較多,可以調節最大群體效用權重v的取值。

5 結論

針對供應商選擇問題,把經典的VIKOR法應用到單值中智環境下,提出了一種基于單值中智VIKOR法的供應商優選模型，主要貢獻有：①推廣了兩個單值中智集的距離公式,提出了廣義的單值中智距離公式,并將其應用單值中智VIKOR法的模型中；②建立了單值中智環境下的VIKOR模型,并通過實例分析驗證了模型的有效性；③對模型進行了靈敏度測試,通過改變決策機制系數進行靈敏度分析，進一步驗證了模型的靈活性、實用性和穩定性。本文方法為多屬性決策問題提供了一種新的觀點，且更通用、更準確。在未來的研究中,如果可以建立計算模型,借助電算化程序，擴大備選方案的范圍,這樣選擇的方案效果更優秀，在未來的研究中將會進一步考慮。