基于變化速率的單變量報警系統設計

曲俊瀟， 王建東， 王 振

(山東科技大學電氣與自動化工程學院，青島 266590)

報警系統是一種監視設備運行工況并提醒工作人員及時處理異常狀況的系統，工業設備安全高效運行的首道保護層及核心組成[1-2]，其性能優劣至關重要，甚至直接關系到環境污染、產品質量、設備損失、經濟效益甚至人員傷亡等問題[3-4]。對于性能較差的報警系統，極易存在報警延遲過長的問題，從而導致操作人員不能及時有效地處理關鍵報警信息。此外，不合理的報警系統可能會造成報警泛濫等問題，大大超出操作人員的處理能力。

現如今, 報警系統的性能優劣越來越受到工業界和學術界的關注[5-6]，EEMUA-191(工程設備和材料用戶協會)指出了報警系統的意義和現狀，同時對報警系統提出了許多要求和指標，是報警系統管理最重要的標準之一[7]。目前，報警系統常用濾波(filtering)、延時 (delay-timers)和死區(deadbands)三種方法來減少漏報率、誤報率以提高報警系統性能。目前，國外學者對報警系統做了大量研究；Rothenberg對過程變量的噪聲進行研究，將報警死區寬度設置為 20%的正常信號噪聲[8]；Hugo[9]為了提高報警系統性能，設置了一種類似于卡爾曼濾波的自適應的報警死區；Hollifield等[10]指出在當代工業報警系統中，大部分報警死區都設置為零；Adnan等[11]使用馬爾可夫過程計算報警死區和報警延時器的延遲時間，并設計了一種權衡誤報率和漏報率以獲得最佳配置的程序；Naghoosi等[12]估計報警抖動指數的方法以設計最佳報警參數；Xu等[13]提出了一種基于均值變化檢測的新方法來估計誤報率和漏報率的概率密度函數的報警延時器設計方法；Adnan等[14]使用馬爾可夫過程計算誤報率、漏報率和平均報警延遲，將廣義報警延時器的性能和靈敏度與傳統的報警延時器進行比較，并提出了廣義報警延時器的概念及其性能指標計算和設計方法；Cheng等[15]在給出報警正常、異常數據統計分布情況下，設計了最優線性FIR報警濾波器；Zang等[16]采用了一種改進的延遲定時器觸發和清除方法來提高報警系統性能，使用馬爾科夫鏈計算改進后的性能指數；Tan等[17]在單變量報警系統中采用秩次濾波器(rank order filters)的方法，給出了報警系統性能指標的計算過程；Chen[18]提出了一種基于相關過程變量的變化方向的多變量報警系統設計方法；Afzal等[19]基于馬爾科夫過程設計了報警死區，并推導出報警死區性能指標的解析表達式。

在中國，報警系統的研究也受到廣泛關注。顧祥柏等[20]提出了基于物元的報警系統可拓重構，并通過基于關聯函數的聚類算法簡化其復雜性。趙勁松等[21]通過數據過濾優化了報警限的設計，大大減少了重復和無效報警。朱群雄[22]對報警系統的監控、優化設計和性能評估等方面的研究進行總結，指出未來報警系統的研究方向，并且通過可視化報警圖解決報警泛濫的問題[23]。付蓉等[24]為控制輸液速度和溫度等信息，提出了一種基于輸液速度與溫度監控輸液的設計。王佳等[25-26]利用時間序列的ARMA(自回歸移動平均模型)模型和時間間隔的均方差模型設計了報警死區和報警延時器，并提出了一個基于模糊理論和數據挖掘算法得到的模糊加權關聯規則挖掘算法用來快速識別報警根源。何乃翹等[27]通過報警系統評估關鍵指標得出報警系統操作員響應性能評價指標。朱群雄等[28]分析了造成報警泛濫的主要原因，總結了報警管理的研究進展。耿雪梅等[29]通過核密度估計法建立考慮人因指標的優化目標函數，設計得到一種報警閾值的自適應優化方法。陳斌等[30]通過多元回歸分析建立了了眼動指標與疲勞的預測模型，通過瞳孔直徑檢測疲勞并報警。徐蕾等[31]提出一種識別人群異常行為的方法，通過人群分布和運動信息加以檢測異常行為而更好的預警。龔安等[32]對單維狀態數據通過時間序列自回歸模型對主泵的異常狀態進行檢測。蔡郁等[33]提出了基于模糊推理和核密度估計來優化報警閾值的自適應調整方法。李俊杰等[34]通過區塊匹配度的關聯分析法解決報警泛濫問題。

對于傳統的單變量報警系統而言，其監控對象是模擬信號的變化幅值，在設計報警死區和報警延時器來優化系統性能時，一般要求過程變量的正常和異常數據段統計分布已知且分布穩定。由于現代工業現場的需要，對變化速率較為平穩的信號可以對其速率進行監控。針對上述問題，提出了一種單變量速率變化的報警系統設計方法，首先通過基于時間序列的線性分段表示法，計算歷史數據模擬信號的歷史變化速率集合時間序列，其次判斷歷史變化速率集合分布是否穩定，然后確定變化速率的報警閾值，最后將在線運行的數據速率與速率報警閾值比較，從而判斷過程信號是否發生異常，若發生異常則應觸發報警，提醒操作人員進行處理。 本文關鍵技術是通過分段線性表示法對模擬信號進行分段減小噪聲干擾和基于貝葉斯估計法判斷歷史變化速率集合的分布穩定性，如何對過程變量進行線性數據段的劃分和如何判斷分布穩定性是本文需要解決的主要重點和難點。

1 問題描述

在現代工業中，傳統的報警系統報警方式如圖 1所示，當過程信號超過上報警閾值或低于下報警閾值時，應觸發報警，即報警信號xa=1；當信號低于上報警閾值且高于下報警閾值時，應消除報警，即報警信號xa=0。但傳統的越限報警方式存在較多的缺點，如監控幅值變化受噪聲干擾較大、報警延遲時間較長、誤報警和漏報警較多等，通常會利用報警死區、濾波器和報警延時器等方法來解決報警泛濫等問題。但對于變化速率較平穩的變量，監測信號幅值的變化往往不能及時發現系統的異常狀態，并且可能會因噪聲的干擾而導致誤報警過多等問題，會浪費大量的人力物力財力，嚴重時會導致重大事故的發生。

圖1 傳統報警方式示意圖Fig.1 Schematic diagram of traditional alarm mode

由于現有的方法并未解決如何判斷所選取的歷史數據分布不再發生變化，導致通過歷史數據所計算的報警系統參數不一定正確；并且對于未發生過報警的變量，無法獲得該變量的異常數據段。針對變化較為平穩的變量，根據監測信號的變化速率設計一種新的報警系統，通過穩定的分布來確定報警系統的參數，以此來提高報警系統的性能。 對于較為平穩的信號如圖2所示，由于存在噪聲干擾，傳統的報警系統僅監控模擬信號的幅值變化，其方式較為單一；并且極易產生誤報警和漏報警，會存在較長時間的報警延遲。

圖2 平穩信號的噪聲干擾Fig.2 Noise interference of stationary signal

研究最終的目的是設計一種基于變化速率的單變量報警系統，具體需要解決的問題如下：①根據數據分布的穩定性確定選取歷史數據的數量并計算速率報警閾值；②計算模擬信號的變化速率，并判斷速率報警器應何時觸發報警。

2 主要方法

主要方法是根據有限的歷史數據，利用基于貝葉斯估計的方法，判斷過程變量的歷史速率集合的分布穩定性，并通過穩定的速率集合計算速率報警閾值。利用等長時間窗口，對窗口內的數據進行線性分段表示，計算窗口內數據的最小二乘擬合結果及斜率的置信區間，并與速率報警閾值相比較，判斷信號的速率變化是否超出正常的速率變化范圍。在當前窗口內的數據完成計算后，將時間窗口滑動一個采樣時間，以達到在線監測過程信號速率變化是否異常的目的。

2.1 訓練數據確定參數

對于速率報警器而言，首先應判斷待測變量的正常運行狀態下歷史數據所獲得的歷史變化速率集合分布是否穩定，即速率樣本的統計分布是否不再改變，然后通過穩定的速率集合確定信號的速率報警閾值。

2.1.1 歷史數據計算斜率

(1)

故式(1)經過計算，解得系數為

(2)

(3)

(4)

(5)

式(5)中：NR為數據個數；σ2為擬合誤差。

(6)

(7)

(8)

(9)

Kmax可由操作人員視情況確定。

2.1.2 確定速率報警閾值

通過正常狀況下歷史數據{xtrain}得到的歷史速率集合{ktrain}，記Ktrain:={ktrain}，數據長度為nk。將{ktrain}的最大值和最小值等長度間隔分為B個小區間，設第b(1≤b≤B)個小區間內包含m個數據，這里通過貝葉斯估計法來估計每個小區間的組頻率概率密度，獲得組頻率的置信區間。此處假設先驗分布為均勻分布。

設第b個區間的組頻率為

(10)

且fb～U(0,1)，即離散概率密度函數為

(11)

式(11)中：M為離散點的個數。則歷史速率集合{ktrain}在fb的條件分布下，似然函數為

(12)

故聯合分布的概率密度函數為

pKtrain,Fb=pKtrain|Fb(k|fb)pFb(fb)

(13)

所以，在k=m時，根據貝葉斯公式，后驗分布的概率密度函數為

(14)

(15)

定義組頻率穩定指標：

(16)

選取穩定分布S0的99.5%和0.5%分位數ktp,H、ktp,L作為速率報警閾值，以確保速率報警器的誤報率不超過1%。

2.2 在線運行

步驟1通過式(7)，計算窗口w內最優分段數損失函數，并根據式(9)求出窗口內數據的最優分段數，將窗口w內第q段分段結果用式(3)線性模型表示：

(17)

(18)

(19)

步驟3定義報警信號為xa，當系統未發生異常時，xa=0；當系統發生異常時，xa=1。在速率報警器中表示為

(20)

3 現有方法

Savitzky-Golay濾波器[40]是一種常用的濾波算法，廣泛應用于工業中數據的降噪處理。Savitzky-Golay濾波的效果隨著選取窗寬和擬合階次的變化而有所差異，可以滿足多種場合的需求。設濾波窗口的寬度為G，各測量點為窗口中心點，即xf={x-(G-1)/2,x-(G-1)/2+1,…,x-1,x0,x1,…,x(G-1)/2-1,x(G-1)/2}，采用mf次多項式對窗口內的數據點進行擬合，每一個點可以表示為不同的多項式的結果，設：

進而得到方程組的最小二乘解估計值

(21)

式(21)中：Xf=[x(i-(G-1)/2),x(i-(G-2)/2+1),…,x(i0),…,x(i(G-1)/2-1),x(i(G-1)/2)]T。將信號經過S-G濾波處理后，應用于報警系統中，減小噪聲的干擾，以此來提高報警系統的性能。

4 方法驗證

通過仿真案例和工業案例，對所提出的速率報警器進行驗證，通過與傳統的報警系統相比較，證明了所提出方法的準確性，并驗證了判斷數據分布穩定方法的有效性。

4.1 仿真案例

首先通過仿真數據驗證基于貝葉斯估計判斷分布穩定性方法的準確性，再利用仿真案例，對比速率報警器與經過S-G濾波的報警系統，以此來說明速率報警器的準確性。

構造數據過程如下：

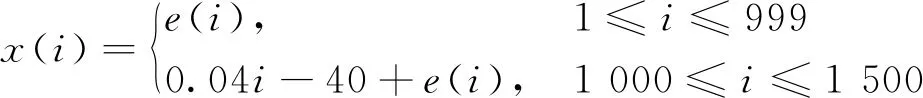
(22)

式(22)中，e(i)服從高斯分布，即e(i)～N(0,1)。系統在i=1 000時發生異常，應觸發報警。這里，假設該信號的高報警閾值xtp=5。根據正常數據段獲得速率集合{ktrain}，且S0={ktrain}。

表1 穩定分布組頻率及置信區間

圖3 仿真案例穩定速率分布的組頻率及其置信區間Fig.3 The group frequency and confidence interval of steady rate distribution of simulation case

繼續增加樣本nadd得到樣本SN，SN的組頻率與分布S0所得置信區間展示在圖4中。表2給出SN組頻率，并計算得出SN的第6～8個區間的組頻率在S0的置信區間內。分布SN的組頻率在分布S0所得置信區間內的概率密度函數面積AN=97.55%，AN>β。

表2 SN的組頻率

圖4 仿真案例S0置信區間與SN組頻率Fig.4 S0 confidence interval and group SN frequency of simulation case

圖5 仿真案例穩定速率分布Fig.5 The simulation case stabilizes the rate distribution

計算所得的仿真案例結果如圖6所示，其中圖6(a)為速率報警器觸發報警時所識別出的數據，圖6(b)為速率報警器檢測速率信號不在正常范圍時觸發的報警信號，所以速率報警器的報警延遲時間為60 s。

圖6 速率報警器仿真案例結果Fig.6 Simulation results of rate alarm

根據第3節中S-G濾波器[40]，通過式(21)得出濾波后的信號如圖7所示。最終，仿真結果得出傳統報警系統的報警延遲時間為113 s。

圖7 S-G濾波器仿真案例結果Fig.7 Simulation results of S-G filter

比較兩種方法得出結論，速率報警器結果準確，受噪聲干擾較小，能及時檢測出信號的異常狀態，且報警延遲時間明顯小于S-G濾波器，整體性能更優。

4.2 工業案例

選取萊城電廠#4機組2015年6月15日8:30—15:10“C磨非驅動端軸承溫度1”信號進行工業數據驗證，該信號規定的報警閾值上限為51。經過第3節所介紹的S-G濾波器計算，得到濾波后的過程信號及報警信號如圖8所示，圖8(a)表示過程信號，圖8(b)表示報警信號xa，當xa=1時，傳統報警系統檢測到異常狀態，觸發報警。

圖8 “C磨非驅動端軸承溫度1”S-G濾波工業案例結果Fig.8 “C-mill non-driving end bearing temperature 1” S-G filter industrial case result

速率報警器的離線計算部分中，根據子節2.1.2中判斷分布穩定性的方法，穩定分布的組頻率及其置信區間上下限如圖9所示，其中紅色區間表示歷史速率穩定分布的組頻率置信區間。

圖9 工業案例穩定速率分布的組頻率及其置信區間Fig.9 Group frequency and confidence interval of steady rate distribution in industrial cases

根據式(16)計算組頻率穩定指數，得到分布SN的組頻率與分布S0所得置信區間如圖10所示，計算所得其面積AN>β。

圖10 工業案例S0置信區間與SN組頻率Fig.10 Industrial case S0 confidence interval and group frequency of SN

最終得到的穩定分布S0的概率密度曲線則如圖11所示。選取穩定速率分布S0的0.5%和99.5%分位數作為速率報警閾值，分別為ktp,L=-0.002 2、ktp,H=0.003 0，繼而進行速率報警器的在線運行。

圖11 工業案例穩定速率分布Fig.11 Steady rate distribution of industrial cases

圖12分別為溫度信號和速率報警器所觸發的報警信號，其中在圖12(a)中，紅色實線表示速率變化異常部分，在圖12(b)中，藍色針狀圖則表示信號速率變化超出正常范圍時所觸發的報警信號。

圖12 “C磨非驅動端軸承溫度1”速率報警器仿真結果Fig.12 Simulation results of “C mill non-driving end bearing temperature 1” rate alarm

圖13表示所得到的信號變化速率，其中紅色虛線為速率報警閾值的上下限。根據圖13 能明顯地看出信號速率的變化與磨煤機軸承溫度信號的變化趨勢大致相同，并且由于引入速率信號置信區間的計算，大大降低了速率報警器的誤報率。

圖13 “C磨非驅動端軸承溫度1”的速率信號Fig.13 Slope of “C mill non-driving end bearing temperature 1”

根據工業案例的結果可知，速率報警器在i=7 110 s時觸發報警，比傳統的報警系統在i=10 124 s時觸發報警提前了3 014 s，并且誤報率明顯低于1%，其性能要優于傳統的報警系統。

5 結論

提出了一種基于速率變化的報警器，該報警裝置作為一個新型的報警裝置，通過貝葉斯估計判斷歷史數據所獲得的速率集合分布穩定，當組頻率基本穩定時，則分布穩定。根據分布穩定的數據分位數，可以獲取速率報警閾值的上下限，并通過滑動窗口法選取數據，利用自底向上法計算信號變化速率，當系統在線運行時，計算窗口內信號速率的置信區間并與報警閾值相比較，判斷系統是否發生異常。最后根據仿真結果和工業案例得出結論：速率報警器不再局限于傳統報警系統只監測模擬信號幅值變化的模式，對信號速率的變化進行監控，尤其對于速率變化較為平穩的信號，速率報警器的性能要明顯優于傳統報警系統，并且可以得到信號變化趨勢，對于操作人員判斷發生異常的原因有著重要的意義。