含風電并網系統魯棒區間優化調度

張 煒, 劉路登, 王海港, 彭 偉, 王 波

(國網安徽省電力有限公司，合肥 230022)

由于風電功率的波動性、隨機性，風電功率難以準確預測，風電的大規模并網對電力系統的安全穩定運行帶來極大的挑戰[1]。為增強電力系統的風電消納能力，提高風電的利用率，一些研究者提出了基于風電功率預測更新的滾動優化調度方法，在線調整機組調度計劃。研究表明此類方法可有效減少風電功率預測誤差造成的電力系統不平衡，提高系統運行經濟性[2-3]。

然而滾動優化調度方法仍然是一種基于“確定性”模型的調度策略，不能直接應對風電功率的不確定性，因此無法保證系統運行的安全性。“確定性”模型使得調度策略的容錯性較差，即使實際風電功率與預測值有較小偏差，調度策略也可行，主要表現在系統備用容量不足、線路傳輸容量不足等方面；當風電滲透率較大時對電網安全運行造成極大威脅[4]。因此，為了有效應對風電功率的不確定性，需要一種“安全”的調度方法。

隨機優化[5-6]和機會約束隨機優化[7-8]是解決電力系統優化調度不確定性問題最常用的方法。然而，隨機優化問題難以求解，只能采用近似算法。此外，還必須給出不確定性參數的概率分布，這在實際應用中是有困難的。

Soyster在20世紀70年代初首次提出了魯棒優化(robust optimization, RO)[9]。一般情況下，魯棒優化模型是一個易于處理的模型。魯棒優化可以看作是隨機優化的一種補充方法，用來處理具有不確定性數據的優化問題。對于一個給定的多參數有界不確定數據集，魯棒優化的最優解應滿足對該不確定集的所有約束[10]。與隨機優化相比，魯棒優化更具優勢，因為它對不確定性參數的需求信息更少，求解更容易。魯棒優化方法的詳細內容見文獻[11]。

魯棒優化方法在許多領域得到了廣泛的應用，其中包括用于解決電力系統優化調度問題。文獻[12]提出具有最小-最大目標的兩階段自適應魯棒優化模型，用于考慮節點注入不確定性的安全約束機組組合問題，并將Benders分解與近似算法相結合來解決該問題。文獻[13]針對不確定價格約束下電力市場的自調度問題，提出了一種基于魯棒優化的最大-最小優化結構自調度模型。利用對偶理論，將該模型轉化為二次規劃問題進行求解。文獻[14]提出了計及抽水蓄能水力發電機組的電力系統魯棒優化方法，該方法具有最大-最小結構，以應對風電功率的不確定性。在以往的研究文獻中，具有最小-最大或最大-最小目標的模型通常用于魯棒優化；其中一個重要的前提：無論風電功率的波動幅值多大，全額被電網吸納。

然而，實際風電功率點預測的精度很低[15]，當風電滲透率較高時對電網的安全穩定運行造成極大的威脅。為了應對風電功率的不確定性，提出了魯棒區間優化調度。風電功率區間預測誤差比點預測誤差低得多；同時棄風現象在某些時段是可行且具有實際意義的調度計劃之必要條件，因為系統可能沒有足夠的備用容量，特別是在夜間的負荷需求低谷時段。只要系統運行安全性得到保障，少量棄風是可以接受的。但在已發表的研究文獻中，沒有考慮棄風量；此外，其所得調度計劃一般采用設定值的形式，這使得風電場的輸出功率難以精確跟蹤；而且，由于調度計劃設定值經常發生劇烈變化，頻繁的調節會降低風力發電機的使用壽命。

本文提出了一種新型的含風電系統魯棒區間優化調度模型，以系統運行經濟性最優、棄風量最小為優化目標，可得到最大允許風電輸出功率區間及常規機組調度計劃。一方面，由于計及棄風量最小，風電功率不能被完全吸納，這有利于緩解風力發電的不確定性，特別是當常規機組的備用容量不足時。另一方面，通過引入輸出功率最大允許區間作為風電場的控制目標，風電場更容易遵循發電計劃，以減少棄風量及風力發電機的調節頻次。

1 魯棒區間優化調度簡介

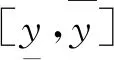
圖1 含風電電力系統魯棒區間優化調度示意圖Fig.1 The schematic diagram of robust interval optimal dispatching of power systems with wind power integrated

含風電電力系統魯棒區間優化調度可歸納為以下模型：

(1)

(2)

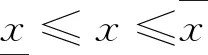
(3)

(4)

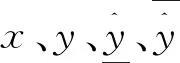
式(2)可轉化為

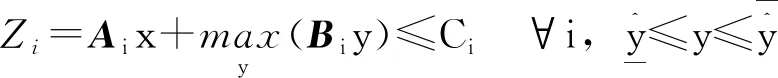
(5)

式(5)中：Ai、Bi分別表示系數矩陣A、B的第i行。

在現實電力系統運行中，由于系統旋轉備用容量限制、輸電斷面容量限制，某些時段可用風電功率不能被全額吸納，因此約束式(4)過于苛刻。可將允許風電輸出功率區間下限設置為小于等于預測風電功率區間下限，即將式(4)修改為

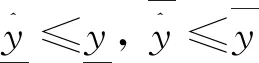
(6)

模型約束式(2)表示電力系統在不確定性因素處于最差場景時的安全約束，是魯棒區間優化調度模型的關鍵。

2 魯棒區間優化調度建模

2.1 最差場景分析

魯棒優化中最差場景是一個參數集合，在除此之外的其他任意場景下求解優化調度模型，得到的調度策略可以保證系統運行的安全性[16]。因此最差場景分析是魯棒區間優化調度建模的必要條件。魯棒區間優化調度模型約束條件包括系統功率平衡約束、輸電斷面潮流約束、旋轉備用約束、爬坡率約束、輸出功率約束等。違反約束條件會導致棄風現象，因此必須滿足以下五個最差場景約束，以保證系統運行的安全性。

2.1.1 向上旋轉備用最差場景約束

(7)

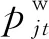
2.1.2 向下旋轉備用最差場景約束

(8)

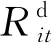
(9)

(10)

2.1.3 常規機組爬坡率最差場景約束

(11)

(12)

(13)

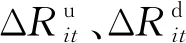
2.1.4 輸電斷面潮流上限最差場景

(14)

2.1.5 輸電斷面潮流下限最差場景

(15)

2.2 魯棒區間優化模型

2.1節描述了在保證系統安全性的前提下，決定最大允許風電輸出功率區間的必要條件，但是在保證安全性的同時必須考慮經濟性。因此目標函數包括兩部分：①常規機組運行成本；②風電場棄風懲罰代價。常規機組運行成本一般表達為輸出功率的二次函數；棄風懲罰代價可以表達為允許風電輸出功率區間與預測風電功率區間差值的比例函數，以達到風電利用率最大化的目的。目標函數具體表達式為

(16)

式(16)中：ai、bi、ci表示常規機組i運行成本系數；t0表示調度計劃的初始時段；T表示調度計劃總的超前時段數；λj表示第j個風電場的棄風懲罰成本系數，基于等微增率原理設置其值[17]。

常規機組運行成本的微增率：

(17)

風電場棄風成本的微增率：

(18)

(19)

式中：ai>0、bi>0，只要λj>0則一定滿足：

(20)

(21)

根據等微增率原理，式(20)、式(21)保證了風電相對于常規機組的優先調度權，因此保證了風電利用率最大化的目標。如果λj對每個風電場取值相同，則系統總棄風量在每個風電場平均分配，因為在優化模型中每個風電場的棄風邊際成本相同。

風電場功率輸出約束：

(22)

(23)

(24)

常規機組旋轉備用容量約束：

(25)

(26)

常規機組爬坡率約束：

(27)

系統功率平衡約束：

(28)

常規機組輸出功率約束：

(29)

魯棒區間優化調度模型歸納如下：

目標函數：式(16)

約束條件：式(7)、式(8)、式(11)～式(15)、式(22)～式(29)

(30)

3 算例分析

3.1 仿真系統設置

在IEEE-RTS系統中進行仿真，使用CPLEX軟件求解模型，驗證所提模型及方法的有效性。

假設此仿真系統包含兩個區域，輸電斷面容量設置為50 MW，表1所示為系統負荷預測值。系統中常規機組的爬坡率設置為機組額定容量的1%；風電場的棄風懲罰成本系數λj設置為50 美元/(kW·h)；系統調度時間間隔設置為5 min。關于IEEE-RTS系統的其他詳細參數見文獻[18]。

表1 負荷預測數據

3.2 含一個風電場系統仿真分析

系統中#13節點接入容量為600 MW的#1風電場，風電場預測輸出功率區間采用某風電場實際數據，并根據#1風電場容量進行等比例調整，表2所示為#1風電場輸出功率區間預測值。關于風電功率區間預測的詳細方法可參考文獻[19-20]。

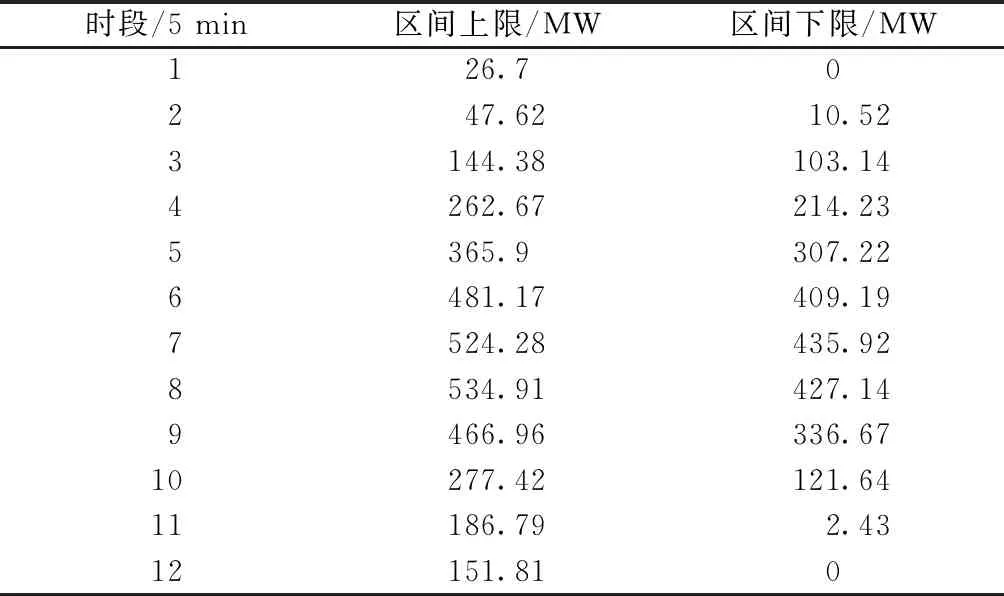
表2 #1風電場輸出功率預測區間

將#1風電場輸出功率區間預測均值作為風電功率點預測值，應用常規經濟調度(conventional economic dispatch, CED)模型進行調度計劃求解[21]，與本文所提模型進行對比分析。

圖2所示為#1風電場的魯棒區間優化調度結果，陰影區域為最大允許風電輸出功率區間，圖2同時展示了應用常規經濟調度模型所得調度計劃。以圖2中陰影區域同樣表示最大允許風電輸出功率區間。

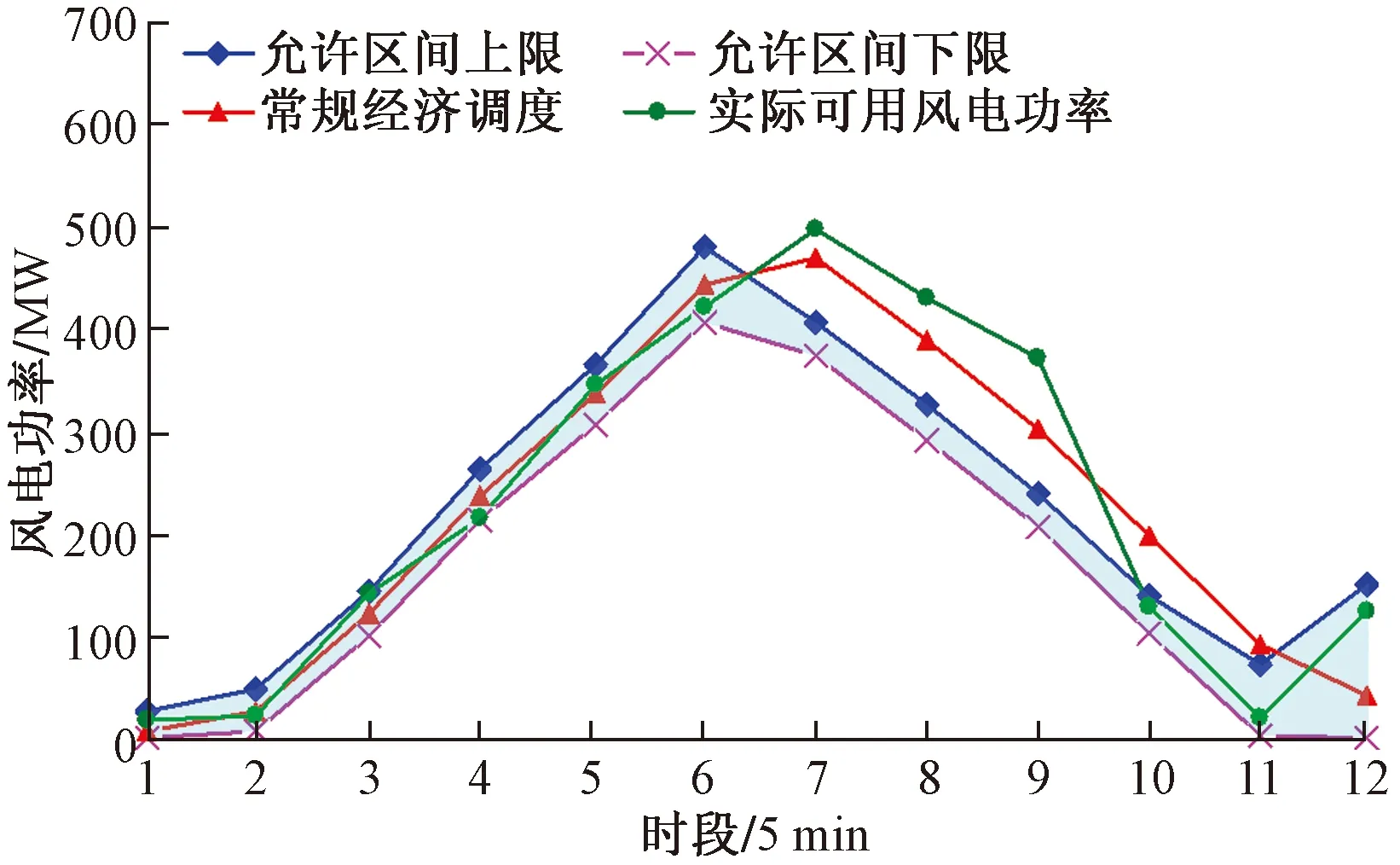
圖2 #1風電場魯棒區間優化調度、常規經濟調度結果Fig.2 Robust interval optimization results for wind farm #1 together with the results of CED

圖3所示為求解魯棒區間優化調度模型所得系統向上、向下旋轉備用容量。

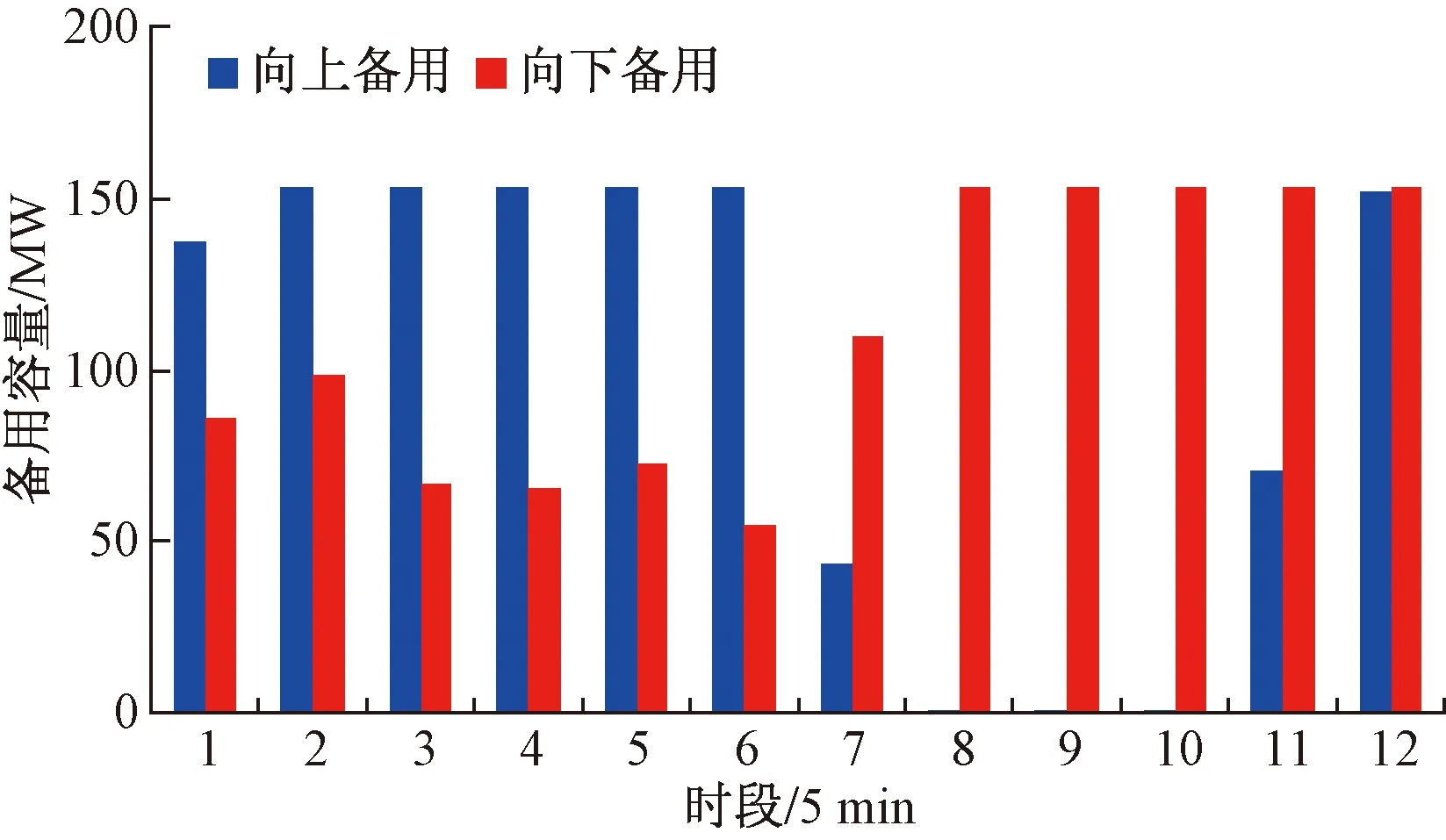
圖3 系統旋轉備用容量Fig.3 Spinning reserve capacity for power system

為了評估不同調度策略下系統運行安全水平，定義安全性指標如下：

(31)

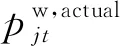
當實際可用風電功率小于調度計劃功率，需要向上旋轉備用容量彌補風電功率差額，如果此時系統向上旋轉備用容量不足，則不能保證系統運行的安全性。反之，當實際可用風電功率大于調度計劃功率，多余風電功率被削減，即棄風現象，不需要額外的系統備用容量。圖4所示為兩種優化調度策略的安全性指標對比，可知在第10、11時刻常規經濟調度模型所得調度策略的系統向上備用容量不足，安全性指標低于安全基準線，不能保證系統運行的安全性，這是因為常規經濟調度模型假設預測風電功率等于實際可用風電功率，而這一假設前提在現實中不可能滿足。

綜合圖2～圖4可作如下分析：

(1)由圖2可知在第7～10時段系統出現棄風現象。在此期間內風電功率下降迅速，由圖4可知此時段內由常規機組提供的向上旋轉備用容量不足以彌補風電功率下降容量，導致棄風。

(2)對比圖2中實際可用風電功率曲線和常規經濟調度曲線可知，兩條曲線有多處交叉點，即風電場必須頻繁調整輸出功率以跟蹤常規經濟調度曲線，這將導致棄風并縮短風力發電機壽命。魯棒區間調度方法可使風力發電機大部分時間處于“最大功率點跟蹤”模式運行，因為除第7～10時段之外實際可用風電功率曲線一直處于可允許風電輸出功率區間內。

兩種調度策略下常規機組運行成本如表3所示。由表3數據可知魯棒區間調度的機組運行成本略高于常規經濟調度的機組運行成本，但魯棒區間調度使系統運行的安全性得到保障，消納了風電功率的不確定性；因此魯棒區間調度運行成本增加0.23%是可以接受的。

表3 不同調度策略下常規機組運行成本

3.3 含兩個風電場系統仿真分析

此案例中在系統#7節點接入容量為350 MW的#2風電場，表4為#2風電場輸出功率區間預測值。

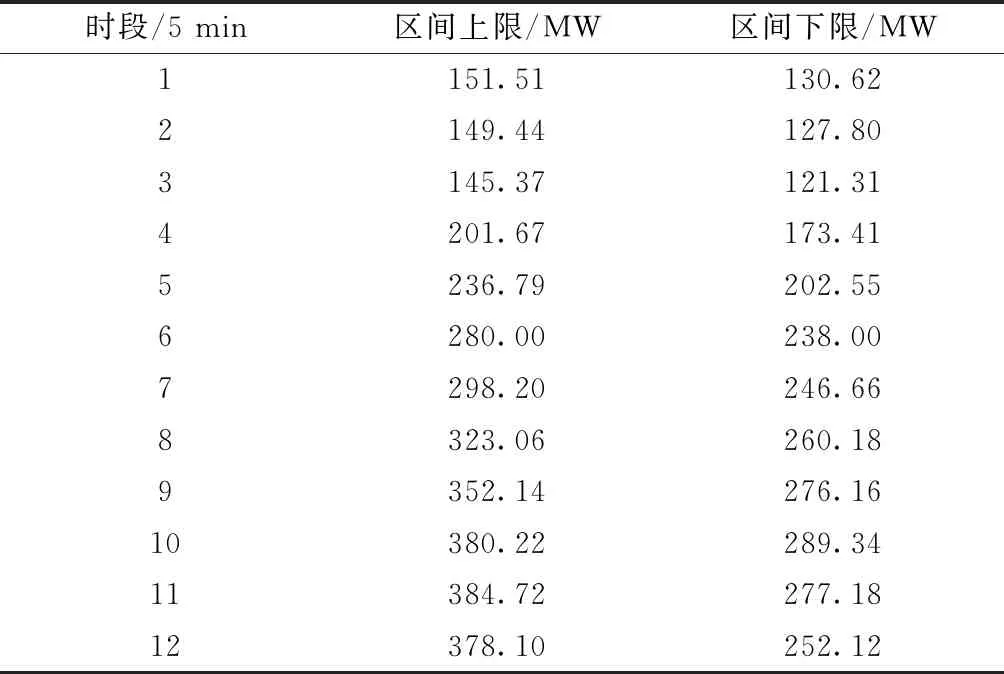
表4 #2風電場輸出功率預測區間

圖5所示為不考慮輸電斷面容量約束時#1、#2風電場魯棒區間優化調度結果。

圖5 不考慮輸電斷面容量約束時風電場魯棒區間優化調度結果Fig.5 Robust interval optimization results for wind farms in the absence of transmission section capacity constraints

對比圖2、圖5(a)可知，#1風電場的最大允許風電功率輸出區間所有擴大，這主要是由于系統中增加了#2風電場輸出功率。多個風電場在較大區域散布使風電功率的輸出相對平滑，即系統中多個風電場的功率互補性有利于風電并網。

圖6所示為考慮輸電斷面容量約束時#1、#2風電場魯棒區間優化調度結果。

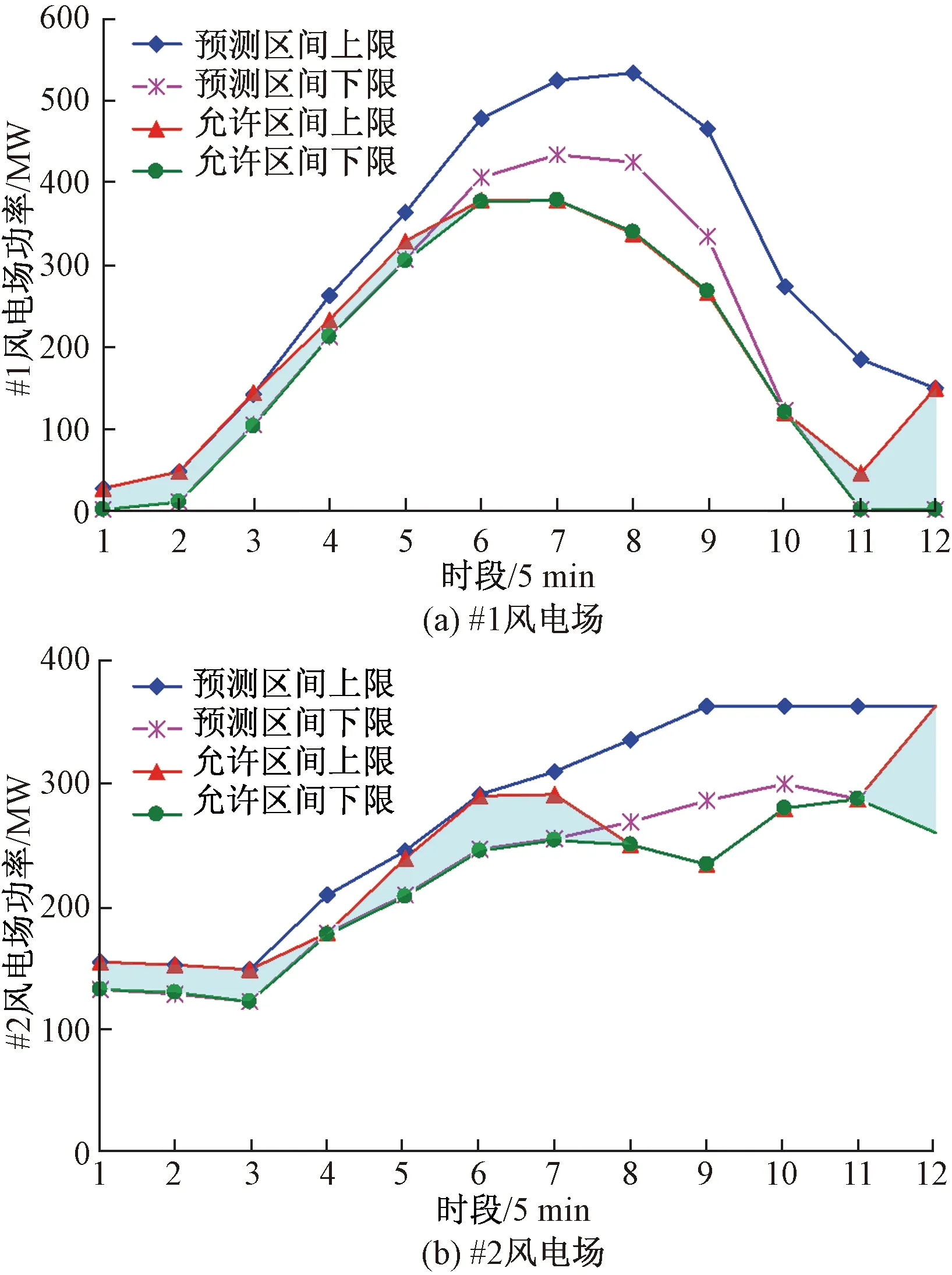
圖6 考慮輸電斷面容量約束時風電場魯棒區間優化調度結果Fig.6 Robust interval optimization results for wind farms considering the capacity constraint of transmission section

圖6(a)與圖5(a)對比分析可知，#1風電場的最大允許風電功率輸出區間縮小。圖6(b)與圖5(b)對比分析可知，#2風電場的最大允許風電功率輸出區間擴大。因為#1、#2風電場處于系統中兩個不同的區域(#1、#2區域)，#1區域至#2區域的輸電斷面容量限制了#1風電場的功率輸出。

4 實例驗證

以中國某省級電網為例，驗證所提模型的有效性。此系統包括2 267個節點，173個常規機組，27個并網風電場，風電場總裝機容量為2 936.3 MW，系統風電滲透率為16.32%，系統最小旋轉備用容量為500 MW，滿足N-1準則。表5為系統負荷預測值。

表5 負荷預測數據Table 5 The predicted load demand data

圖7所示為省級電網中風電魯棒區間優化調度結果。分析圖7可知，在時段1～4、16～24、28～45出現了棄風。在時段1～4、16～24系統負荷較高，而風電功率急速下降，由于常規機組向上爬坡率的限制，向上爬坡容量不足導致棄風。在時段28～45系統負荷很低，常規機組輸出功率維持在最低水平，系統基本無向下備用容量，而此時段可用風電功率較高，因此出現棄風。

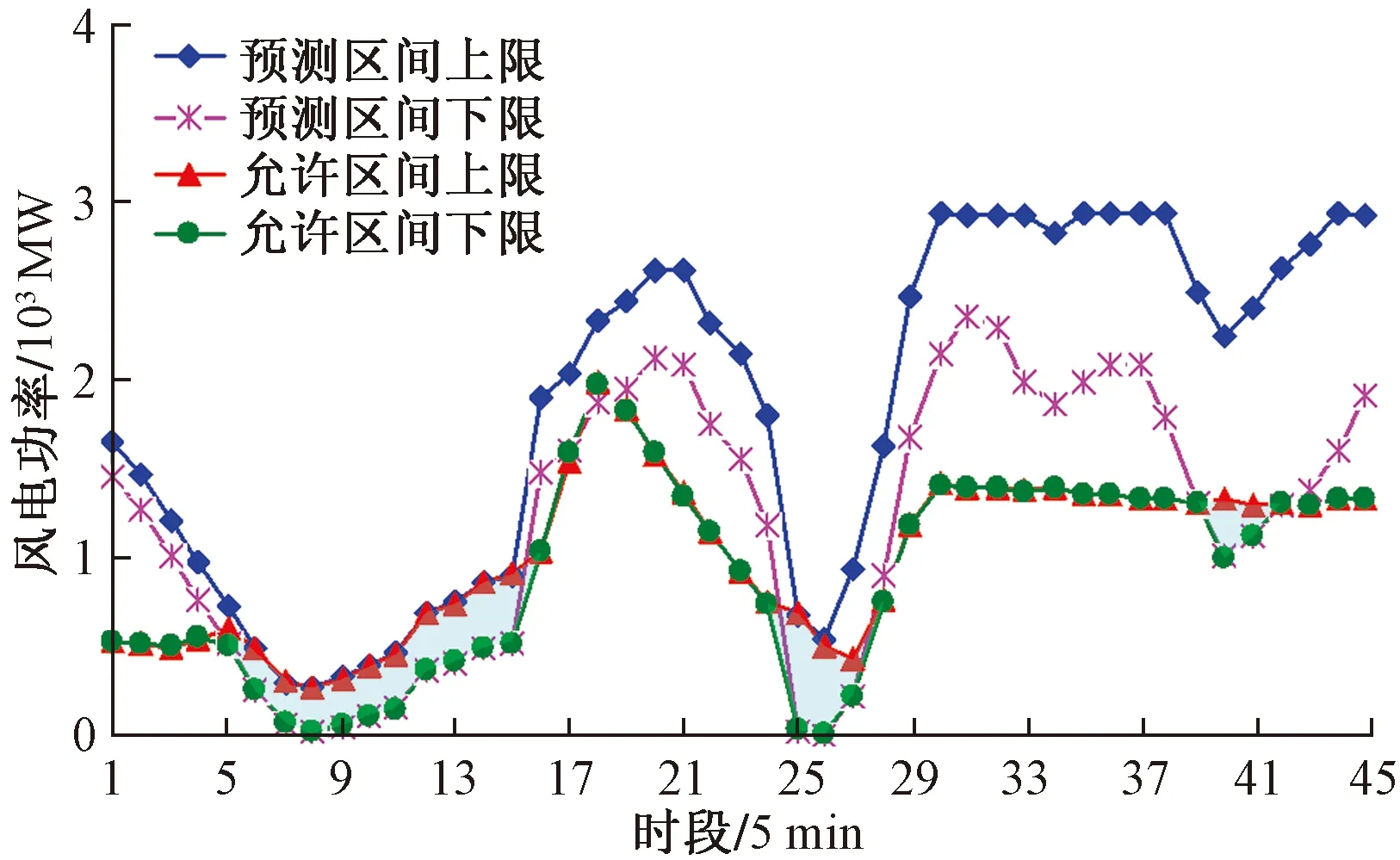
圖7 省級電網中風電魯棒區間優化調度結果Fig.7 Robust interval optimization results for the wind power in provincial power grid

5 結論

(1)提出了含風電并網系統魯棒區間優化調度模型，對最差場景安全約束進行了詳細分析，同時計及系統運行經濟性。求解該模型可得到風電場的最大允許輸出功率區間及常規機組的最優經濟調度計劃。

(2)在IEEE-RTS系統中的仿真結果及省級電網的實例驗證結果表明，該模型所得系統調度策略的魯棒性及安全性最優。通過引入風電場最大允許輸出功率區間作為控制目標，可有效降低棄風量、減少常規機組輸出功率調節頻次；增強系統的風電消納能力。

(3)當風電功率預測誤差較大時，該模型所得風電場最大允許輸出功率區間相對保守，出現少量棄風，系統運行成本比常規經濟調度稍微增加。因為該模型約束要保證每一個最差場景的系統安全性，一些最差場景的發生概率極低，導致調度策略相對保守。因此未來可依據風電功率區間預測的概率屬性對模型進行改進，保證系統安全性的同時進一步提高經濟性。