基于多層節點模型的平流層浮空器熱力學分析

鄧小龍， 麻震宇， 楊希祥， 朱炳杰

(國防科技大學 空天科學學院， 長沙 410073)

平流層浮空器是指利用輕于空氣的浮升氣體產生的浮力在平流層底部進行持久駐空飛行的浮空類飛行器，主要包括平流層飛艇和高空氣球，具有飛行時間長、搭載能力強、使用效費比高等優點.平流層浮空器在全天候、全天時的信息獲取應用中具有顯著優勢，可為對地觀測、通信保障、防災減災、環境監測等應用需求提供重要的技術解決方案，具有巨大的軍民應用前景[1].

由于駐空高度附近的大氣密度極低，采用浮升力維持駐空飛行的平流層浮空器體積通常較龐大，浮空器囊體內部氣體狀態的變化在較大程度上影響了浮空器的性能特征.超熱超壓是平流層浮空器長期駐空所面臨的一項關鍵問題.駐空飛行期間，浮空器蒙皮以及內部浮升氣體的溫度和壓力主要受太陽輻照、大氣環境等因素的影響，對浮空器的溫度和壓力的控制直接關系到浮空器駐空高度保持能力的提升[2].同時，浮升氣體的超熱現象會導致囊體超壓，過大的超壓量將會導致囊體破裂，引發結構安全性的重要問題.囊體材料受溫度不均勻分布會產生熱疲勞和局部熱應力，進而影響囊體壽命[3].因此，熱特性研究是平流層浮空器實現長時駐空安全飛行的重要工作.

實際上，熱特性長期以來都是平流層浮空器的研究熱點.在熱模型研究方面，主要有零維模型、一維模型、二維模型、三維模型.

零維模型將整個浮空器等效為質點，囊體與浮升氣體視為一體.零維模型可用于分析平流層浮空器升降過程中的平均溫度變化[4]，分析蒙皮熱輻射特性對浮升氣體溫度的影響，仿真分析指出太陽輻射吸收率和紅外輻射發射率在晝間期間對浮升氣體溫度的影響明顯[5].

一維模型將整個浮空器視為上下兩節點或三節點.兩節點模型研究表明，晴天條件下飛艇內氦氣晝夜間的溫度差約為51 K[6]；三節點模型被用于分析平流層飛艇的蒙皮和浮升氣體的熱特性，內部浮升氣體晝夜間溫度差為58.8 K，上部蒙皮的晝夜間溫度差為65.8 K，下部蒙皮的晝夜間溫度差為51.9 K[7].二維模型將浮空器視為平面進行分析，二維無限長圓柱模型被用于分析飛艇的溫度變化[8]，其中考慮了太陽輻射和紅外輻射的影響，采用經驗公式計算了對流換熱.利用三維模型建立浮空器全尺寸模型，通過大量網格劃分利用有限元方法或有限體積方法進行計算.三維模型被用于計算平流層浮空器囊體的三維穩態溫度場，研究囊體材料輻射特性和云層環境對材料和氦氣溫度的影響[9]，研究太陽輻射、地球大氣紅外輻射和外部對流換熱等環境下的內部表面輻射和對流換熱[10].

綜上所述，不同的熱模型考慮了不同的熱影響因素和不同的幾何復雜性.兩節點模型較為簡單，可用于快速分析平均溫度特征，三維模型相對精確，但需要大量計算分析.本文提出基于多層節點的平流層浮空器熱模型，通過建立太陽輻射、天空地面紅外輻射、對流換熱等熱環境，為平流層浮空器的熱特性分析提供基礎.

1 熱力學模型

平流層浮空器的熱環境包括太陽直射輻射、天空散射輻射、地面及云層反射輻射、大氣長波輻射、地面長波輻射和對流換熱以及內表面之間的輻射和內表面與浮升氣體之間的對流換熱.平流層浮空器熱環境示意圖如圖1所示.其中：β為蒙皮第i單元的外法線方向和太陽直射光線向量的夾角；θ為蒙皮第i單元外法向與水平面之間的夾角，且法向向上為正.

圖1 平流層浮空器熱環境Fig.1 Thermal environment of stratospheric aerostat

用位于i等份兩端的水平面截取球體，得到單元i，當N足夠大時，單元i內的蒙皮受熱情況近似相同，即熱力學性質相同.實際上，由于太陽輻射方向與球體坐標的相對夾角，一般各層受到不均勻輻照程度，考慮到模型的簡化及快速計算，本文通過加權平均方法假設各層所受輻照均勻.

由于蒙皮厚度小，忽略蒙皮單元間的熱傳導，將超壓球體等效為由N個灰體面元組成的封閉腔體.

則蒙皮第i單元的熱平衡方程為

QIRI,i+QCE,i+QCI,i)

(1)

式中：mi為第i單元的質量；ci為第i單元的比熱容；Ti為第i單元的溫度；QDN,i、Qd,i、QR,i分別為第i單元吸收的直射、散射和反射輻射；QIRE,i和QIRI,i分別為第i單元外、內表面長波輻射吸熱；QCE,i和QCI,i分別為第i單元的外部對流與內部對流吸熱.

氦氣的熱平衡方程為

(2)

式中：cv為氦氣的定容比熱；W為單位時間內氣球做的膨脹功；mHe為氦氣質量；THe為氦氣溫度.

太陽直射輻射強度是指在垂直于太陽光射線的表面上，單位時間內投射到單位面積上的太陽直射輻射強度為

IDN=I0τam

(3)

式中：I0為大氣層外的太陽輻射強度；τam為大氣透過率.

蒙皮第i單元吸收的太陽直射輻射為

QDN,i=ηAiIDNcos(π-β)

(4)

式中：η為蒙皮太陽輻射吸收率；Ai為蒙皮第i單元面積.當β∈(π/2, π)時，表明第i單元在氣球的上半部分.當β∈(0,π/2)時，蒙皮第i單元位于浮空器下半部分，吸收的太陽直射輻射為

QDN,i=γηAiIDNcosβ

(5)

式中：γ為蒙皮材料的太陽輻射透射率.

蒙皮第i單元吸收的天空散射輻射為

Qd,i=ηAiId(0.5+0.5sinθ)+

γηAiId(0.5-0.5sinθ)

(6)

式中：Id為天空散射輻射強度.

蒙皮第i單元吸收的地面及云層反射輻射為

QR,i=ηAiIR(0.5-0.5sinθ)+

γηAiIR(0.5+0.5sinθ)

(7)

式中：IR為地面與云層的反射輻射強度.

蒙皮第i單元的外表面長波輻射吸熱為

(8)

式中：ε為蒙皮發射率；σ=5.67×10-8為Stefan-Boltzmann常數；φ為第i單元與地面的角系數；Tair為大氣溫度；Tg為地面溫度；εsky為天空等效發射率；εg為地面長波輻射發射率，取εg=0.9；τiw為地面長波輻射的大氣透過率.且有：

φ=1-(0.5+0.5sinθ)

其中：pvap為空氣中水蒸氣分壓力；p0為海平面大氣壓力；pair為環境大氣壓力.

由于浮空器視為N個灰表面組成的封閉腔體，內表面為漫反射，蒙皮內表面長波輻射吸熱QIRI,i為

QIRI,i=(Ji-Gi)Ai

(9)

式中：Gi和Ji分別為第i單元的投射輻射力和有效輻射力，且有

蒙皮第i單元內外表面吸收的對流換熱為

(10)

式中：ΔTair-fil和ΔTHe-fil分別為環境大氣與蒙皮溫度差、氦氣與蒙皮溫度差；hCE,i和hCI,i分別為第i單元的外表面和內表面的對流換熱系數,采用如下公式計算：

l為傳熱面的特征尺寸，取l=2r；K為傳熱系數；λ為導熱系數，取空氣、氦氣熱導率為

球體外表面對流的熱系數為

KCE=

(11)

球體內表面對流換熱系數為

KCI=0.021Ra2/5

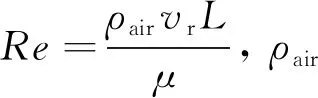
2 算例結果與分析

首先，分別采用零維模型、有限元離散模型和多層節點模型，對文獻[8]的飛艇熱試驗進行仿真計算.其中，零維模型將浮空器考慮為一個節點，有限元離散模型劃分6 000個二維矩形單元，多層節點模型劃分40個節點.計算結果表明：零維模型和多層節點模型的計算時間較為接近，均為秒量級，有限元模型計算時間達到35 min；有限元模型與試驗結果的最大誤差為1.2 ℃，多層節點模型最大誤差為2.5 ℃，零維模型最大誤差達到5.6 ℃.綜合考慮計算效率和精度，多層節點模型更有優勢.

在此基礎上，本文對美國國家航空航天局(NASA)的超長航時超壓氣球(ULDB)開展了多層節點方法的浮空器熱特性分析.該浮空器采用南瓜形超壓囊體，其主要設計參數如表1所示.飛行工況為飛行時間2018年6月21日，最大駐空高度31 km，經緯度為40°N、88°E，仿真中考慮來流速度為 5 m/s.

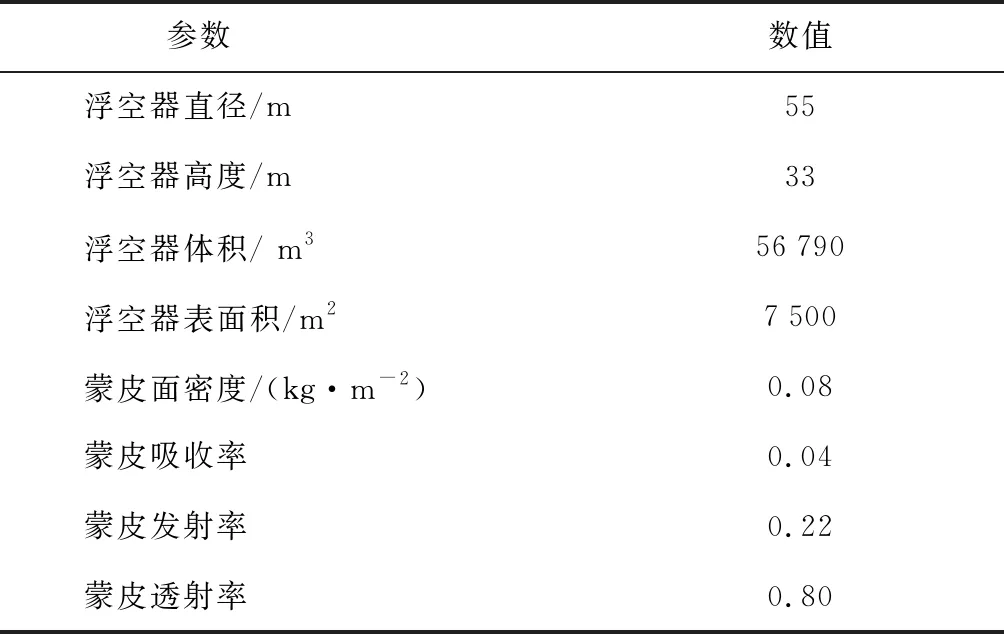
表1 ULDB參數Tab.1 Parameters of ULDB

根據多層模型的熱力學模型，設置分層為40層，通過Runge-Kutta方法對熱力學模型的微分方程進行求解，仿真計算獲得的浮空器內氦氣平均溫度Tave、蒙皮頂部溫度T1、蒙皮底部溫度T2曲線如圖2所示.由圖2可知，氦氣的夜間溫度為222 K，白天最高溫度為267 K，晝夜溫差為45 K；在夜間，由于地面長波輻射的影響，底部蒙皮溫度為224 K，略高于頂部蒙皮的221 K，這與平流層飛艇的底部蒙皮和頂部蒙皮溫差表現有較大的差異.文獻[11]對平流層飛艇的熱特性分析指出，蒙皮上下表面的夜間溫度差達到了50 K，這主要是由于平流層飛艇蒙皮材料是采用多層復合柔性織物材料，其熱特性與高空氣球的多聚物材料有顯著區別.該結果也說明，在平流層浮空器總體設計中，應綜合考慮浮空器搭載設計要求和熱特性帶來的超熱效應.在白天，蒙皮的最高溫度為274 K，蒙皮最大溫差為13 K，蒙皮溫差也明顯小于平流層飛艇的上下表面溫差.蒙皮及浮空器內氦氣的全天溫度均高于外界環境溫度，白天氦氣溫度大于最底端的蒙皮溫度，但與底端蒙皮溫度更接近.由圖2可知，氦氣在夜間的平均溫度及頂部與底部蒙皮的溫度均保持不變，夜間穩定溫度分別為232.2 K、224.3 K和243.5 K.這是因為在夜晚外界環境溫度及熱輻射環境保持相對穩定.

圖2 ULDB溫度曲線Fig.2 Temperature of ULDB

基于分層模型的熱力學分析方法，其本質是考慮浮空器不同部分傳熱方式的影響程度對實際溫度分布的影響.下面研究分層數量對于熱力學分析的影響.分層數量M為2、10、20、40時氦氣溫度的計算結果如圖3所示.由圖3可知，隨著分層數量的增加，計算得到的氦氣溫度有所增加，且逐漸收斂.對于2層模型，此時與雙節點模型類似，計算得到的氦氣溫度在全時段內均低于多層數模型.2層模型的氦氣最高溫度為255 K，而40層模型的氦氣最高溫度為267 K，溫差達到13 K.因此，多層節點模型的節點劃分是計算精度的重要參數.

圖3 不同層數下多層模型計算的ULDB內的氦氣溫度Fig.3 Helium temperatures of ULDB at different layer numbers

在平流層浮空器設計及其應用中，工作高度是一個非常重要的輸入條件.不同高度處的大氣密度差異不僅影響浮空器的浮力，還影響浮空器的熱交換環境，因此有必要分析平流層浮空器在不同駐空高度的熱特性.平流層浮空器在20 km、25 km及31 km駐空高度Hst上的氦氣溫度曲線如圖4所示.由圖4可知，駐空高度對于氦氣溫度有顯著影響.高度越高，外界環境溫度有所升高，且大氣密度的降低將降低對流換熱能力.相對于31 km處的氦氣溫度最高值(267 K)，浮空器處于25 km和20 km時氦氣溫度的最高值分別降低為260 K和250 K.因此，降低駐空高度可在一定程度上降低氦氣溫度.

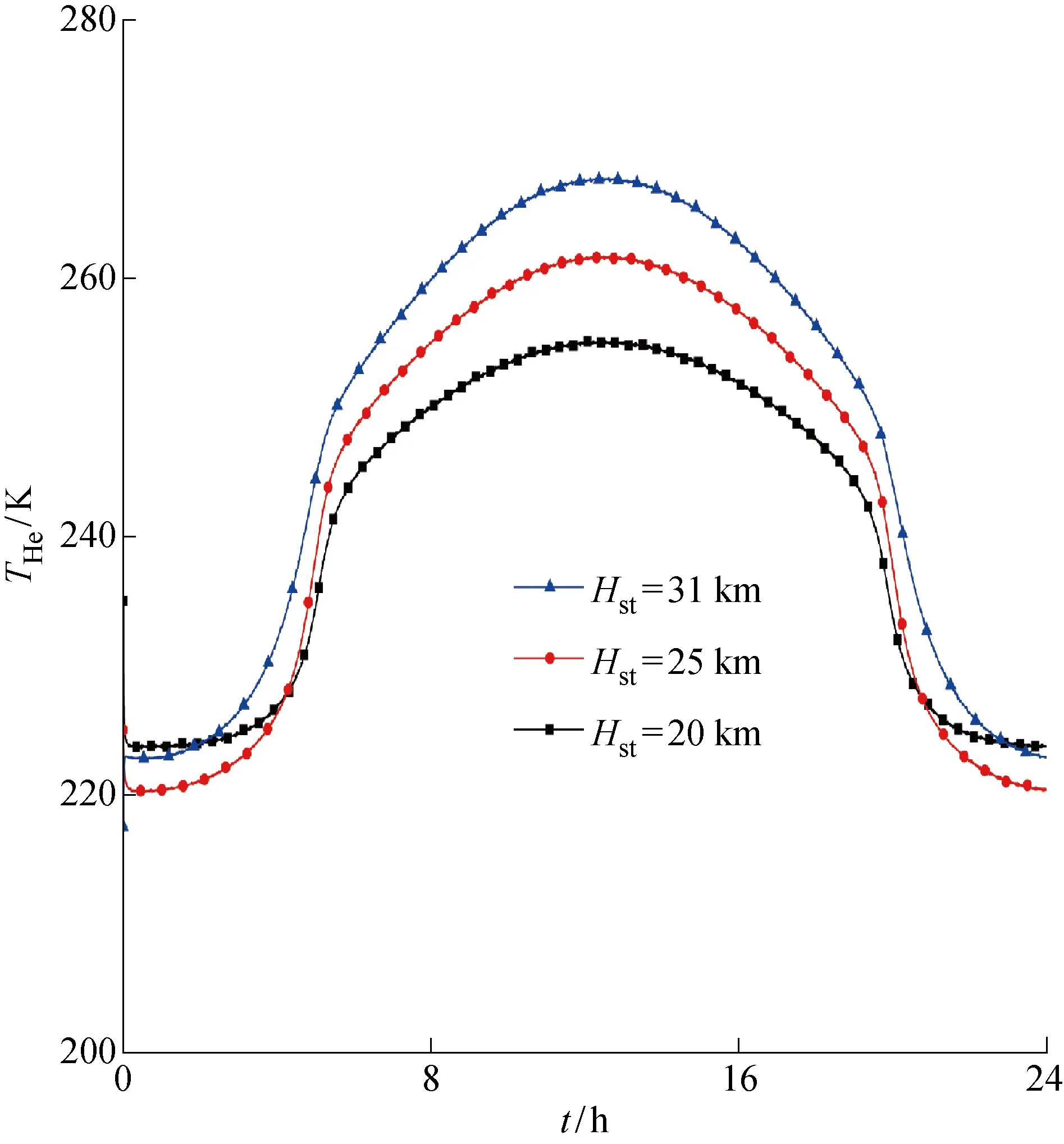
圖4 ULDB在不同駐空高度的氦氣溫度Fig.4 Helium temperatures of ULDB at different altitudes

考慮到高空氣球、平流層飛艇等平流層浮空器均需要在不同區域執行相應的任務，有必要分析平流層浮空器在不同緯度ψ地區的熱特性影響.平流層浮空器在低緯度至高緯度地區(20°N、40°N、60°N、80°N)的氦氣溫度曲線如圖5所示.由圖5可知，緯度位置對于氦氣溫度有著非常重要的影響.緯度越低，相應的氦氣晝夜溫差越大.在高緯度地區，氦氣的晝夜溫差僅約6 K.這主要是由于高緯度地區的極晝現象，使得浮空器所處的輻照環境的晝夜差異較小.因此，對于工作在高緯度極地區域的平流層浮空器，常見的超熱超壓問題并不突出，所需要的抗超壓能力較小.

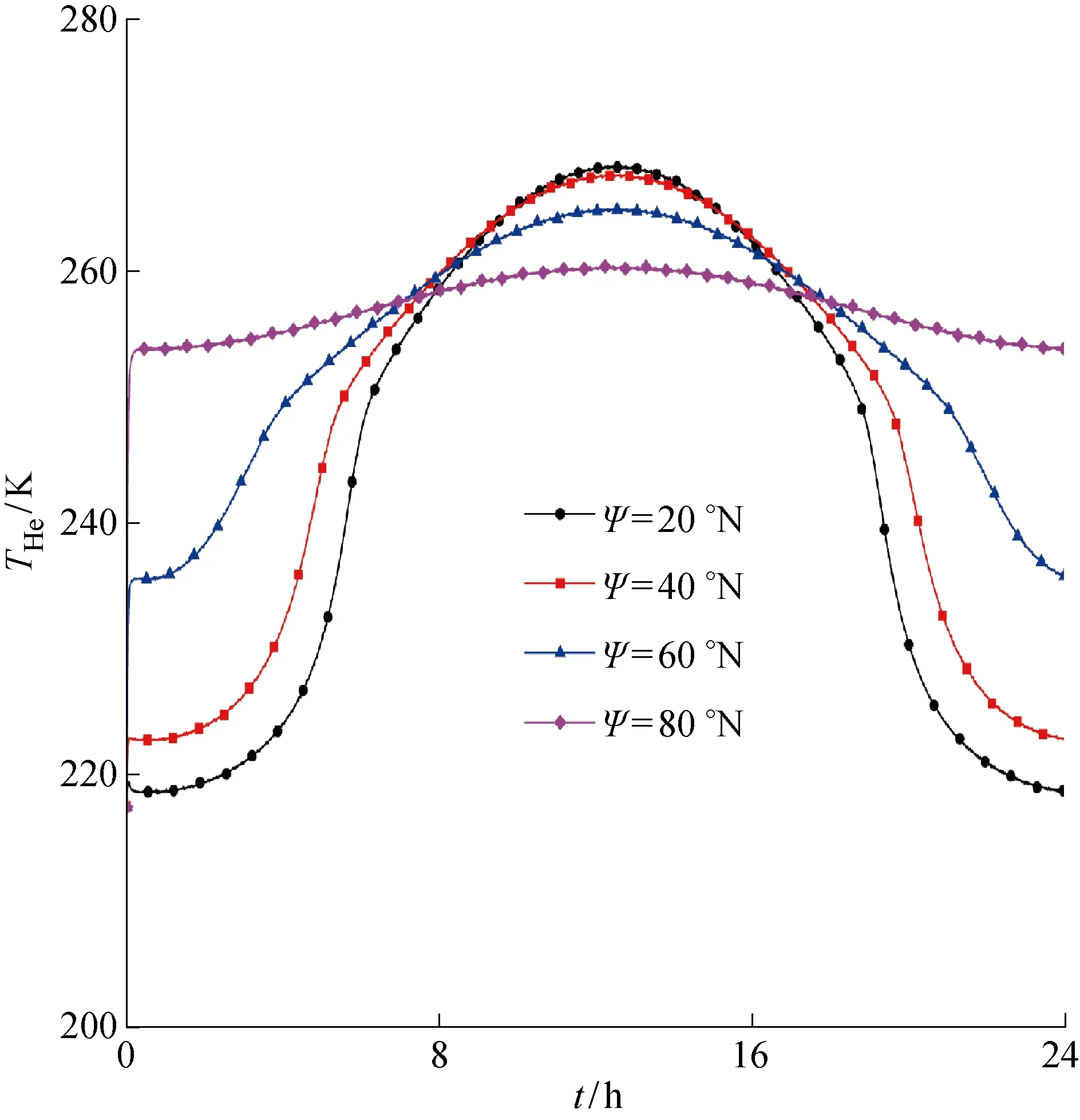
圖5 ULDB在不同緯度的氦氣溫度Fig.5 cHelium temperatures of ULDB at different latitudes

3 結論

本文基于多層節點方法對平流層浮空器駐空階段的熱力學特性開展了研究，獲得以下結論：

(1) 建立了用于平流層浮空器熱特性分析的多層節點模型，將浮空器沿豎直方向均分為多層，考慮了太陽輻射、浮空器與天空及地面的長波輻射、蒙皮間長波輻射、蒙皮與大氣對流換熱、蒙皮與氦氣自然對流等因素.

(2) 針對NASA的超長航時超壓氣球模型進行數值仿真，結果表明，浮空器存在明顯的超熱現象，氦氣晝夜溫差達45 K；但與平流層飛艇相比，超長航時超壓氣球的上下表面蒙皮溫差不大.

(3) 分析了平流層浮空器在不同駐空高度的熱特性.結果表明，駐空高度的變化對氦氣溫度作用明顯，駐空高度由31 km降至20 km時的氦氣溫度可減小17 K.

(4) 分析了平流層浮空器在不同緯度地區的熱特性.結果表明，緯度位置對氦氣溫度有著重要的影響.緯度越低，相應的氦氣晝夜溫差越大.在高緯度地區，氦氣的晝夜溫差僅約6 K.