基于支持向量機回歸的曲面零件渦流測距標定方法

陶正瑞， 黨嘉強， 徐錦泱， 安慶龍 陳 明， 王 力， 任 斐

(1. 上海交通大學 機械與動力工程學院； 機械系統與振動國家重點實驗室， 上海 200240； 2. 上海航天設備制造總廠有限公司， 上海 200245)

隨著無損檢測技術的發展，渦流檢測以其具有非接觸、無污染、易于實現自動化等優點在航空航天可靠性檢測、鐵道車輛及軌道質量檢測、發動機包覆層、金屬基體材料表面油漆等涂覆層厚度測量中有著廣泛的應用[1].根據經典的渦流位移測量理論[2-3]，渦流位移傳感器只能測得物體表面一部分區域(1.5～2倍探頭盤徑)到傳感器探頭端面的距離.因此當被測表面為平面時，可以獲得比較理想的結果，但渦流測距問題的研究對象正由平面向復雜曲面方向發展.目前，渦流測距是建立在線圈平板互感效應上的一種無損檢測方法，被測金屬表面為平面時可獲得理想的測量精度.然而在實際應用中，渦流位移測量問題的研究對象正由平面向曲面發展，使用平板標定結果測量曲面零件精度往往達不到要求，基于曲面近似平面的假設得到的測量結果非常不準確.

近些年國內外的研究雖取得了一定的成果，但主要集中在使用電渦流傳感器對曲面零件探傷和測厚方面，如重要結構件探傷、檢測管道等零件涂層厚度.Thompson[4]采用脈沖渦流法定量檢測多層結構內部的腐蝕問題.Mitra等[5]提出采用多頻渦流檢測技術開展飛機部件搭接結構中的缺陷成像研究.曾亮[6]利用渦流法檢測特種碳纖維復合材料絕緣涂層，測得的有效測量范圍約為30～800 μm，測量精度絕對值約為 20～30 μm.姜磊等[7]使用電渦流法測試應力作用下碳纖維復合材料的位移，獲得應力水平對傳感器靈敏度的影響規律.

針對電渦流位移傳感器的曲面位移測量問題，目前的相關研究較少.胡鵬[8]基于涂鍍層厚度檢測問題，研究以平板標定結果測量曲面零件表面涂鍍層厚度，研究結果表明該方法檢測誤差大，完全不具有實際應用價值.李德維等[9]設計了一種基于電渦流位移傳感器的車輪形狀測量方法，得到傳感器對正曲率與負曲率曲面實測值與標定值的誤差分析結果，但只概括性地給出曲面幾何形狀對電渦流位移測量輸出特性影響規律的定性分析.由于沒有建立數學模型，無法進一步定量分析渦流位移傳感器的測量誤差.高寬厚等[10]提出一種雙層導電涂層厚度的電磁無損檢測方法，厚度檢測誤差低于10%，但其理論推導和試驗驗證都是針對平面零件的.

基于上述問題，本文以燃料貯箱筒段外表面聚氨酯泡沫層的厚度測量為例，開展4種常見筒段試件標定試驗.由于聚氨酯泡沫不導磁、不對磁場產生影響，試驗對象采用未噴涂聚氨酯泡沫的曲面試件，標定試驗過程中將厚度測量轉化為距離測量.提出基于支持向量機回歸的標定方法，以上述標定數據為樣本建立提離距離預測模型(LDPM).需要注意的是，標定試驗流程通過渦流位移傳感器逐步向上提離試件表面以模擬不同厚度的泡沫層，因此被稱為提離距離預測模型.研究曲率對渦流測距測量誤差的影響規律，按誤差產生的原因可以將測量誤差分為兩部分：表面曲率誤差和其他誤差.分析各部分誤差在傳感器量程范圍內的分布規律，為曲面零件渦流測距誤差補償提供參考依據.此外，對比分析LDPM與4次多項式擬合和5項Gaussian函數[11]擬合兩種常用標定方法在測量精度、計算速率方面的優劣，為曲面零件渦流測距選用何種標定方法提供建議.

1 試驗方案

1.1 試驗設置

根據燃料貯箱筒段外表面聚氨酯泡沫層厚度的測量要求：常用筒段曲率范圍為0～0.9/m，傳感器量程范圍內的測量誤差控制在 ±0.5 mm以內.選取4種典型尺寸的曲面被測試件：曲率半徑分別為1.125 m(N1)、1.675 m(N2)、3.000 m(N3)以及平面(N4)，材料均為鋁合金6 063，表面粗糙度Ra=6.4 μm.

試驗系統主要分為測量模塊與數據采集模塊.測量模塊包括電渦流位移傳感器、被測曲面試件、傳感器固定夾具、高精度機床；數據采集模塊包括數據采集卡和數據顯示屏幕.通過夾具將電渦流傳感器探頭固定于高精度機床主軸，機床主軸移動改變提離距離，數據采集卡實時采集傳感器的輸出電流信號，并由PC上位機顯示和保存.試驗系統的總體結構如圖1所示.傳感器選用的是上海冉普電子科技有限公司生產的RP6660電渦流位移傳感器，其性能參數如表1所示.

表1 電渦流傳感器技術指標Tab.1 Technical indicators of eddy current sensor

整體測量位于美國赫克公司生產的HURCO VMX42五軸立式加工中心，機床參數如表2所示.

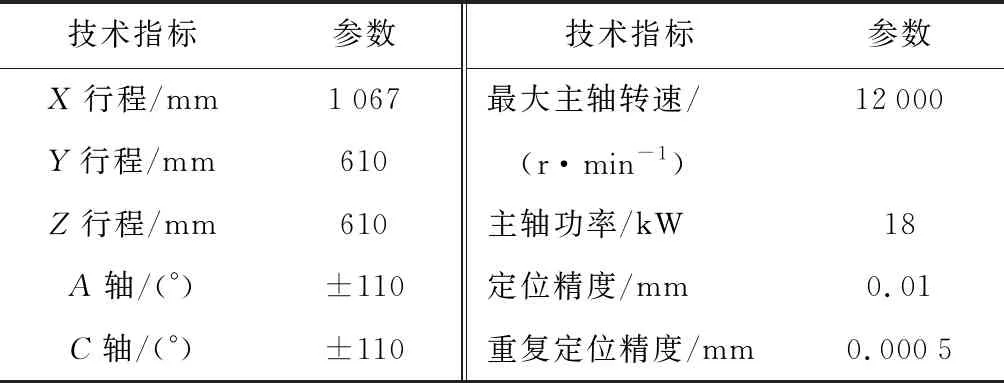
表2 機床性能參數Tab.2 Machine tool performance parameters

使用USB5001數據采集卡實時釆集傳感器輸出的電流信號I，如圖2所示.其中：t為采集時間；采樣頻率設為1 kHz.

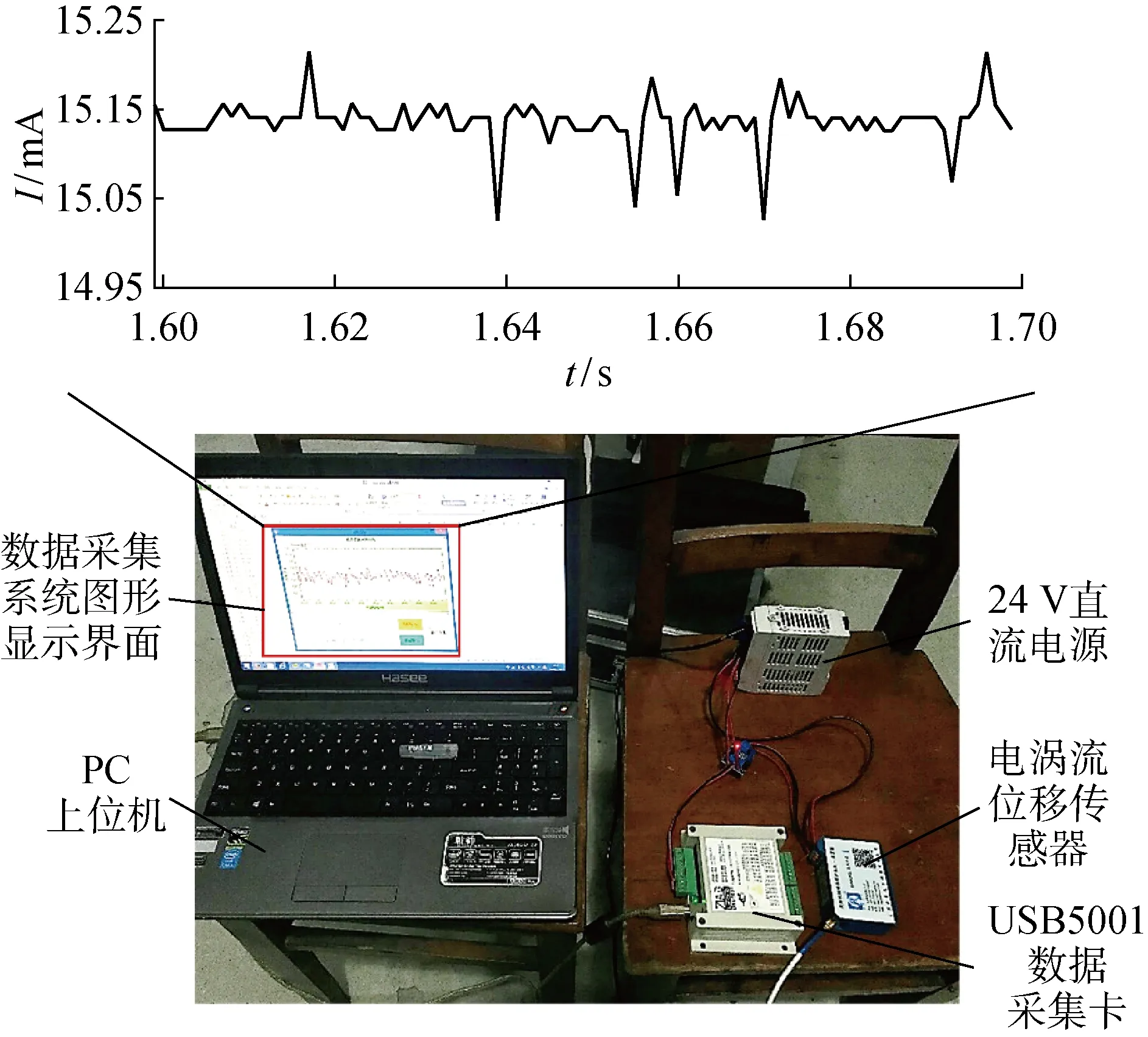
圖2 數據采集模塊Fig.2 Data acquisition module

試驗現場設置如圖3所示，將傳感器探頭通過夾具夾持并固定于機床主軸， 確保探頭位于被測試件正上方且探頭軸線沿試件曲面法線方向.傳感器探頭與被測試件需嚴格按照圖3的位置關系安裝定位，否則定位誤差會導致極大的測量誤差，使標定數據不可靠.

1.2 試驗方案

首先確定測量起始位置，手動控制機床主軸沿Z軸移動至量程范圍內鎖住主軸Z向，主軸沿Y向以最小進給量緩慢移動，找到傳感器示數最小的Y向位置，鎖住主軸X、Y向，使主軸以最小進給量沿Z軸緩慢接近被測試件表面.當0.03 mm的塞尺剛好不能塞入探頭與試件表面間的縫隙時，停止進給，將提離距離0.03 mm作為起始位置.在傳感器量程范圍內，每隔0.5 mm改變一次提離距離，將傳感器輸出電流信號和提離距離作為標定數據樣本點.為減少測量誤差，每個提離距離截取1 s穩定測量階段的信號數據(即 1 000 個數據點)，對輸出電流波形濾波去噪，然后取平均值，即為該提離距離對應的渦流信號.為減少隨機誤差，每種曲面試件從起始位置到量程終點每個位置按上述操作重復測量5次取平均值.需要注意的是，每次更換曲面測試件后都需要對傳感器探頭重新找正與定位.

1.3 數據預處理

對試驗獲得的渦流信號預處理，如濾波去噪、取均值等.以提離距離y=20.53 mm為例，使用移動平均濾波器對信號進行平滑處理，窗寬為30個樣本點，濾波結果如圖4所示.電流信號平均值為15.3 mA時代表y=20.53 mm，兩者構成數據集中的一個樣本點.以此類推，可以獲得傳感器量程范圍內，每個提離距離所對應的電流信號.

圖4 電流信號的平滑濾波Fig.4 Smoothed and filtered current signal

2 基于支持向量機回歸的標定方法

支持向量機回歸(SVR)是高效的監督學習方法，能夠兼顧模型的復雜性和學習能力、最小化經驗誤差和最大化幾何邊緣，在解決小樣本、非線性及高維模式識別中表現出獨特的優勢[12].

訓練數據可表示為

{xi,yi},i=1,2,…,n,yi?R,xi?RD

(1)

式中：xi為數據樣本特征，對應曲率和渦流信號；yi為數據樣本標記，對應提離距離；D為數據維度，此處D=2；n為樣本數，此處n=490.

對于非線性的SVR問題，可以通過映射函數φ(·)，將輸入數據映射到高維特征空間F中[13]

f(x)=w·φ(x)+b

(2)

式中：w為權重向量；b為常數；f(x)為回歸預測模型輸出，其與yi之間存在一定的誤差，可通過損失函數來評價模型預測的好壞[14].需要解決的優化問題可用下式表示

(3)

|y-f(x)|ε=max{0,|y-f(x)|-ε}

(4)

(5)

式(5)即為最終的標定函數表達式，其中k(xi,x)為核函數.

本文以曲面試件N1、N2、N3、N4標定試驗數據為樣本，基于SVR的標定方法，建立LDPM.對于常見曲率范圍0～0.9/m，LDPM的輸出結果如圖5所示,其中κ為曲率.由圖5可知，提離距離隨電流信號的上升而增加.在傳感器量程初始階段，等高線沿著曲率軸方向波動，在I=4 mA處達到最大，與最小提離距離相差3 mm；當I=15.5 mA時，等高線基本和曲率軸平行，曲率和提離距離的相關性并不明顯；在傳感器量程終點區域，等高線從左上角往右下角傾斜，說明渦流位移傳感器在相同的提離距離下，曲面零件曲率越大，輸出的電流信號越小，即傳感器的最大提離距離與曲率呈正相關，曲率越大，傳感器的最大提離距離越高.

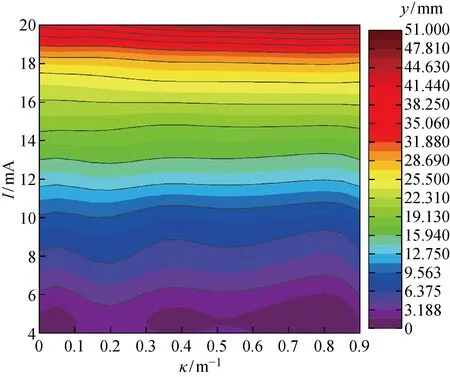
圖5 基于支持向量機回歸的提離距離預測模型Fig.5 Lifting distance prediction model based on support vector machine regression

下面研究LDPM在N1、N2、N3、N4上的測量誤差，定量分析曲率對測量誤差以及誤差分量的影響規律.

(1) 對于同一曲率，LDPM的測量誤差Δy與y的關系基本呈三角函數關系變化，如圖6所示.對于精度要求較高的應用場合，選取誤差曲線與Δy=0相交處的y作為關鍵位置.曲面試件N1、N2、N3的測量誤差曲線與平面試件N4的誤差曲線差異明顯，因此將平板標定的結論用于曲面零件渦流測距會產生較大的測量誤差.

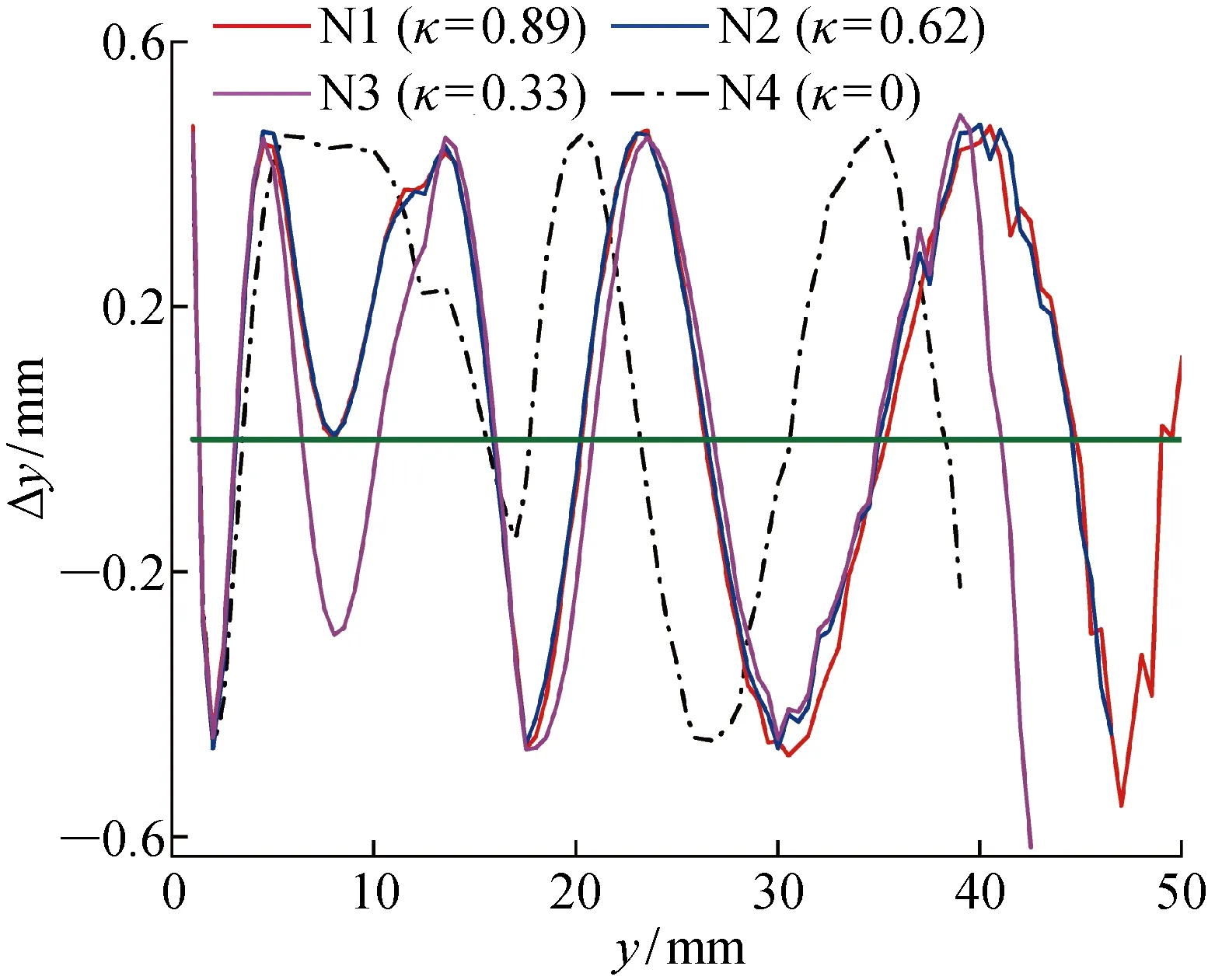
圖6 Δy隨y和κ的變化規律Fig.6 Δy versus y and κ

(2) 將測量誤差按產生的原因分為兩類：受被測試件表面的曲率影響產生的測量誤差值簡稱表面曲率誤差Δyκ；其他誤差Δyo包括溫度漂移、機床定位誤差、數據采集卡A/D轉換誤差以及標定過程中電渦流探頭安裝定位誤差.表面曲率誤差和其他誤差在傳感器量程范圍內的分布如圖7所示.其中，其他誤差為LDPM在N4上的測量誤差；N1、N2、N3的表面曲率誤差等于測量誤差減去其他誤差.表面曲率誤差和其他誤差在整個傳感器量程范圍內交替變化，分布在Δy=0兩側且呈現出相互抵消的趨勢，N1、N2、N3的表面曲率誤差曲線近似為多個周期和幅值不同的余弦函數拼接而成.在傳感器量程起點區域a內，N1、N2、N3的表面曲率誤差曲線為單周期的余弦函數且幅值較小，其他誤差占主導，3種曲面試件的測量誤差曲線重和性較好，如圖6所示；而在區域b內，N1、N2、N3的表面曲率誤差曲線幅值和周期均有所增大，此時其他誤差維持在最大值附近，3種曲面試件的測量誤差位于Δy=0上方；在測量中點附近區域c，N1、N2、N3的表面曲率誤差達到最大值，其他誤差近似于正弦函數，誤差相互抵消；在終點區域d，N1、N2、N3的表面曲率誤差幅值接近為其他誤差的1.5倍，超過其他誤差占主導地位.

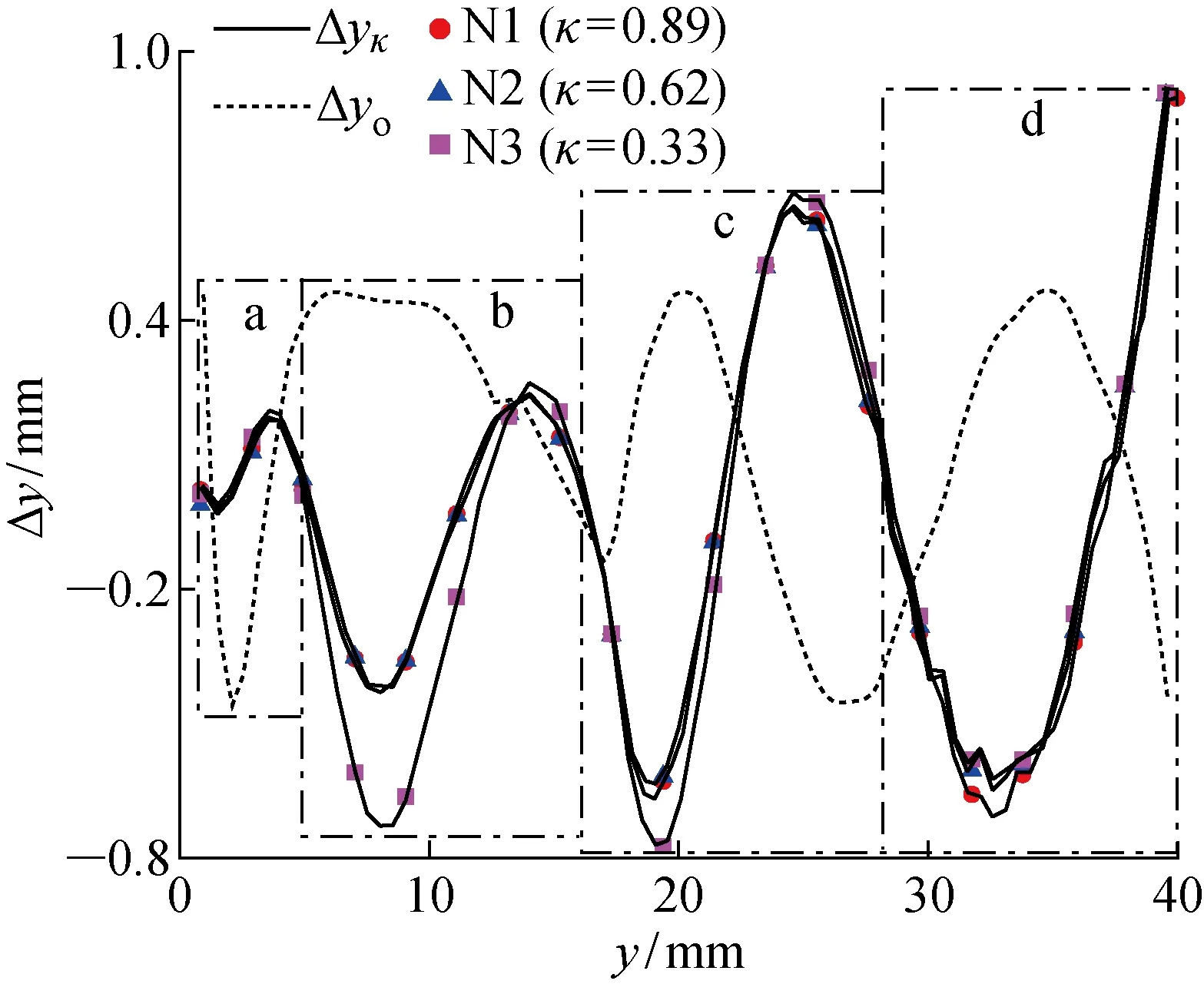
圖7 Δyκ及Δyo的分布Fig.7 Distribution of Δyκ and Δyo

(3) 研究曲率對表面曲率誤差的影響規律.不同區域a、b、c、d處，表面曲率誤差隨著曲率的變化規律會有所區別，如圖7所示.在傳感器量程起點區域a內，表面曲率誤差曲線重合，表面曲率誤差與提離距離的變化趨勢相同，對曲率不敏感；在區域b內，N1、N2的表面曲率誤差曲線基本重合，但N3的表面曲率誤差曲線始終位于其下方，具體表現為相同的提離距離，表面曲率誤差絕對值隨著曲率的增加而減小；在測量中點附近區域c，3種曲面試件的表面曲率誤差曲線在大部分位置重合，但在峰谷等位置處差異明顯，具體表現為相同的提離距離，表面曲率誤差絕對值隨著曲率的增加，先減小后上升；在終點區域d，表面曲率誤差絕對值隨著曲率的增加而上升.

在量程范圍內通過補償其他誤差來減小測量誤差，具體通過分析誤差分量正負號的變化規律，為曲面測量誤差補償提供依據：當正負號相反時，兩者的綜合效果會使總測量誤差下降，此時停止補償其他誤差；當正負號相同時，以通過補償其他誤差的方法來減小測量誤差.以N1為例，誤差補償前后測量誤差的變化如圖8所示，補償之后的誤差曲線更接近Δy=0.

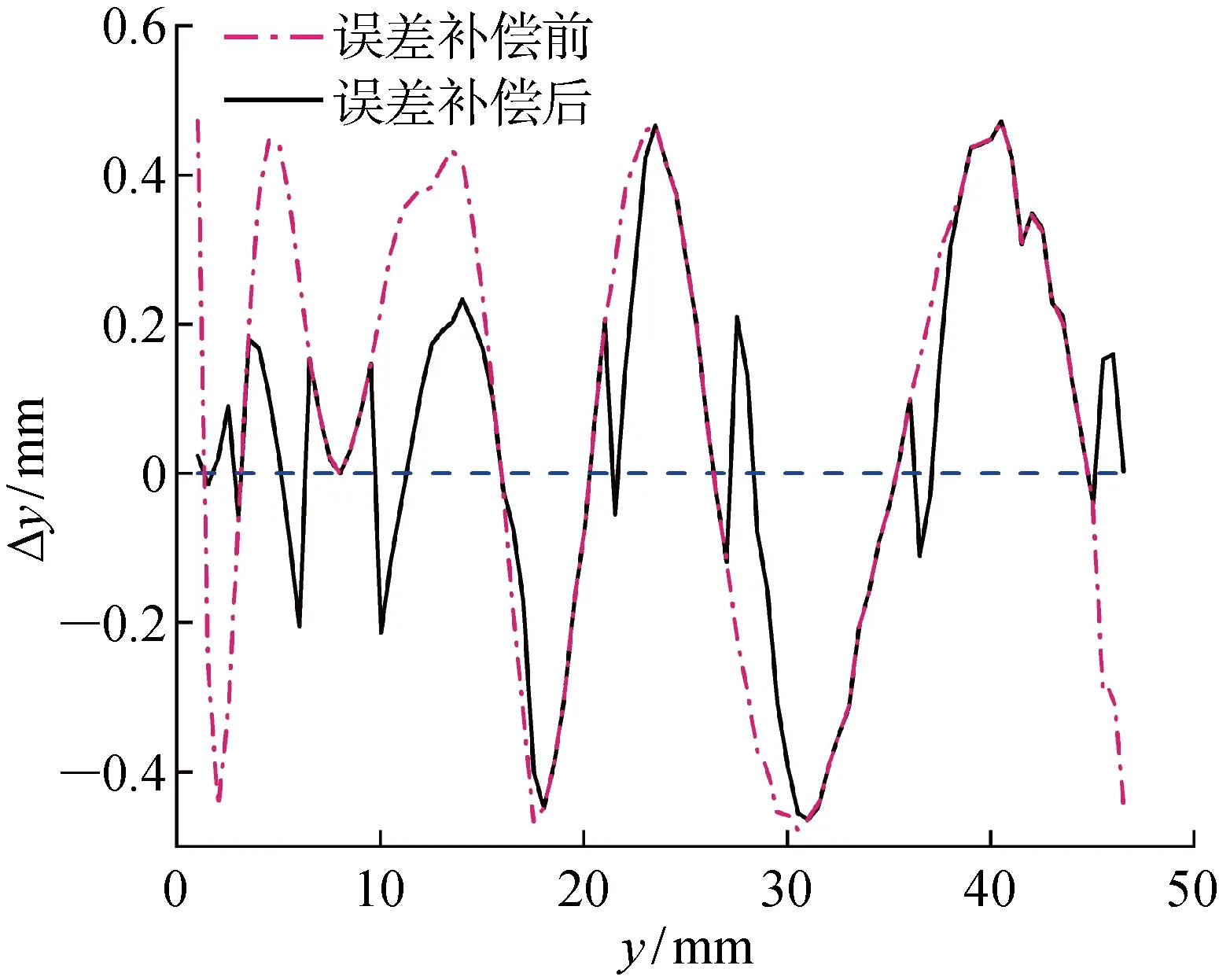
圖8 誤差補償前后模型的Δy變化Fig.8 Variation of Δy before and after error compensation

使用誤差平方和(SSE)來衡量預測值與樣本點的接近程度，SSE越接近于0，LDPM的精度越高.

(6)

式中：pi表示分布率，此處取為1；fi表示樣本點i處的標定結果，yi表示樣本點i處的真實提離距離.N1、N2、N3誤差補償前的誤差平方和SSEbe與誤差補償后的誤差平方和SSEaf，以及補償前的最大誤差絕對值MAEbe和補償后的最大誤差絕對值MAEaf的對比如表3所示，其中σ為下降量.對于N1、N2、N3，誤差補償前后的SSE分別下降了41.5%、43.6%以及41.4%；MAE下降了1.1%、2.5%以及3.2%，LDPM的輸出結果更接近真實提離距離.

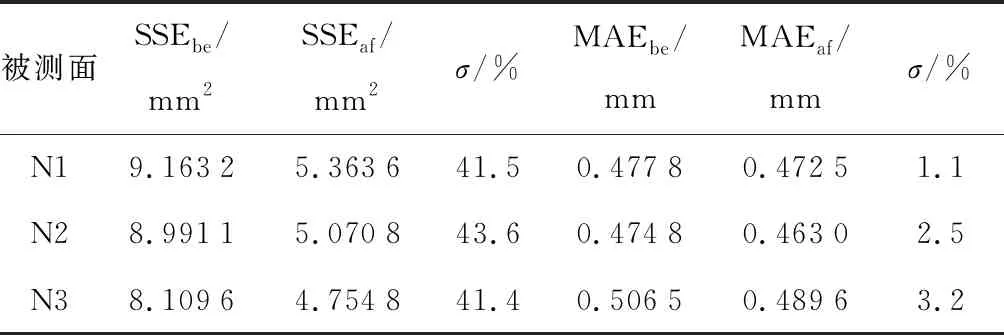
表3 N1、N2、N3誤差補償前后預測效果比較

3 LDPM與典型標定方法的比較

在實際應用過程中，針對曲率范圍內常用的幾種曲率試件做標定試驗，將得到的LDPM用于渦流測距系統的標定函數.而典型標定方法如多項式擬合、多峰Gaussian擬合標定，也常用于確定標定函數.不同之處在于，LDPM可適用于整個常用的曲率范圍，而常用標定方法確定的標定函數參數只針對特定曲率有效，對于不同的曲率需要重新標定更新參數.下面針對N1，對比分析LDPM、4次多項式擬合(Poly4)以及5項多峰Gaussian函數擬合(Gauss5)[11]，以SSE、均方根(RMSE)為評價指標，對比分析不同的標定方法.

均方根表示樣本數據點相對于標定曲線的離散程度[16]，

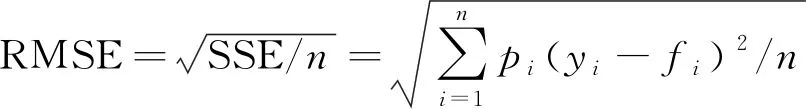
(7)

LDPM和不同標定方法的誤差對比如圖9所示，LDPM與4次多項式擬合和5項多峰Gaussian函數擬合的誤差統計分析如表4所示.其中η為預測誤差下降量.

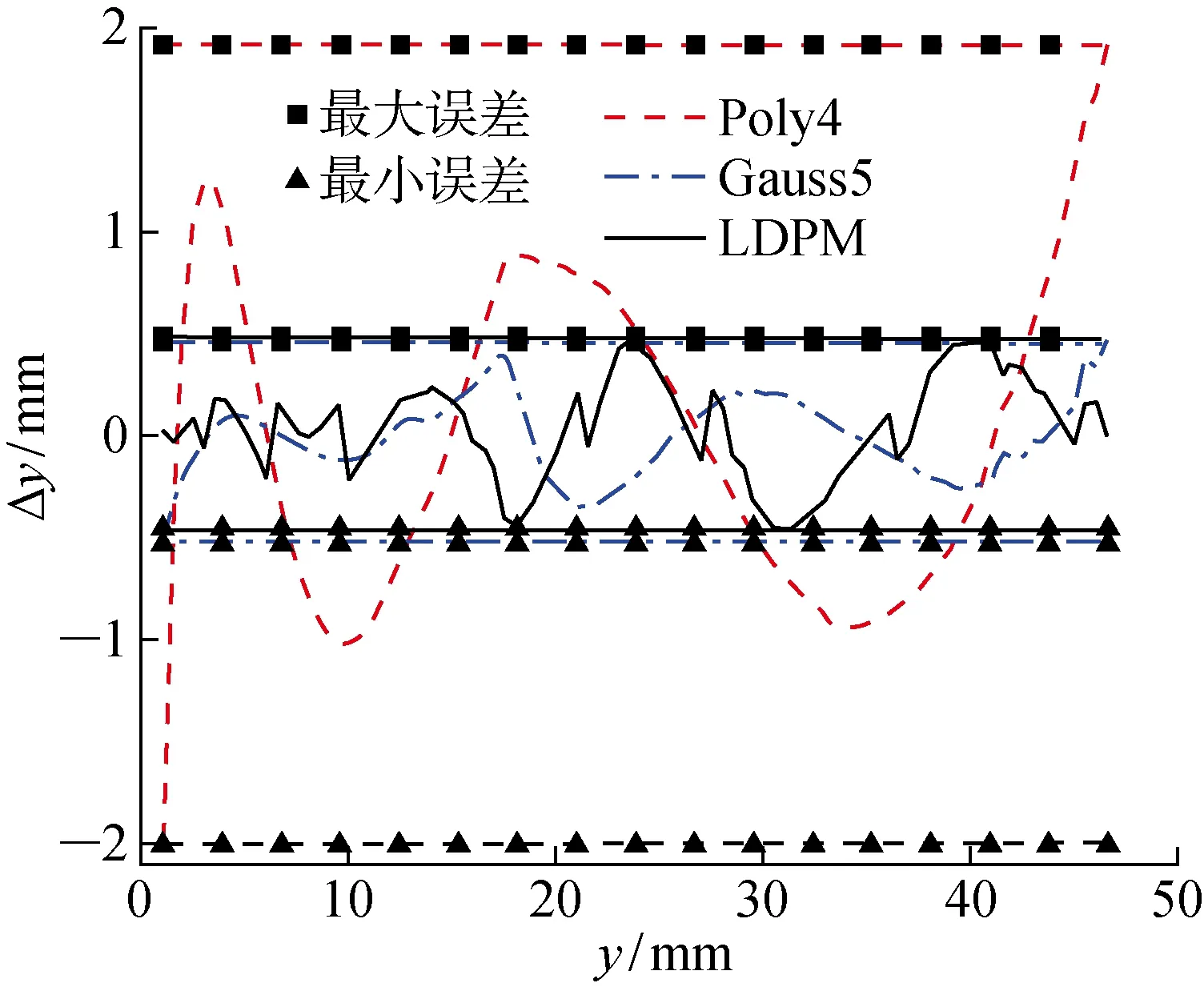
圖9 LDPM與不同標定方法的誤差對比Fig.9 Error comparison among LDPM and other methods

由表4可知，LDPM測量精度高于4次多項式擬合，相比較而言，SSE下降了90.4%，RMSE下降了69.0%以及MAE下降了76.3%.與5項多峰高斯擬合相比，SSE下降0.4%，RMSE下降0.2%以及MAE下降8.4%，兩者的測量精度相當.

表4 不同標定方法的誤差統計分析Tab.4 Statistical analysis of errors for different calibration methods

此外，運算速度也是選擇何種標定方法的一個重要指標，不同標定方法因計算復雜程度不一，運算速率也有差異，比較上述3種方法平均單點運算時間.隨機取100個測試電流的數據，使用MATLAB中的tic和toc函數得到總運行時間進而獲得單點運算時間，運行環境為Windows10、MATLAB R2016b，運算結果為：Poly4的運算時間為0.542 s；Gauss5的運算時間為1.178 s;LDPM的運算時間為2.452 s.

LDPM與4次多項式和5項Gaussian函數擬合相比，單點運算時間是4次多項式擬合的4.52倍，是5項Gaussian函數標定方法的2.08倍.適用于采樣頻率不超過407 Hz、測量精度高的應用場合.當然，上述比較結果只是提供了相對的大小關系，渦流測距系統的最終采樣頻率還要考慮其他因素的影響，包括數據采集模塊的數據處理能力、通信方式的選擇等.

4 結論

本文分別針對曲率半徑為1.250、1.675、3.000 m曲面試件以及平面試件進行標定試驗，提出基于SVR的標定方法，建立LDPM用于曲面零件的渦流測距，分析測量誤差分量的分布規律，提供誤差補償策略，并與常用的標定方法在測量精度、運算速率等方面進行比較，結論如下：

(1) 針對曲面零件渦流測距，LDPM的輸入為測量電流信號值(4～20 mA)、被測試件的曲率(0～0.9/m)，輸出是距離值.針對該型號的電渦流位移傳感器，LDPM的誤差可以控制在[-0.5, 0.5] mm，精度與5項多峰Gauss擬合相當，高于4次多項式擬合，能夠滿足一般應用場合需要，簡化了標定流程，具有重要的應用價值.

(2) 根據誤差產生的原因將測量誤差分為兩部分：表面曲率誤差和其他誤差.LDPM在傳感器量程初始階段0～5 mm，表面曲率誤差曲線重和性較好，曲率對表面曲率誤差影響不敏感；在范圍5～16 mm，表現為在提離距離相同時，表面曲率誤差絕對值隨著曲率的增加而減小；在測量中點附近區域16～28 mm，誤差曲線在大部分位置重合，但在峰谷等位置處差異明顯，具體表現為相同的提離距離，表面曲率誤差絕對值隨著曲率的增加，先減小后上升；在終點區域，表面曲率誤差絕對值隨著曲率的增加而上升.

(3) 在整個量程范圍內的不同測量區間，其他誤差保持不變，可以通過補償其他誤差來減少測量誤差，分析兩個誤差分量的相對大小變化規律，為曲面測量誤差補償提供依據：當處于其他誤差和表面曲率誤差的正負號相反的測量區間時，兩者的綜合效果會使總誤差減小，此時停止補償其他誤差；當處于其他誤差和表面曲率誤差的正負號相同的測量區間時，此時可以通過補償其他誤差的方法來降低總誤差.

(4) LDPM的單點運算時間約為2.45 ms，是4次多項式擬合的4.52倍，限制了渦流測距系統的最終采樣頻率.因此，在實際應用過程中需要結合不同應用場合的采樣頻率需求判斷該方法是否合適.