基于蟻群算法西安旅游路線的優化研究
李夢丹
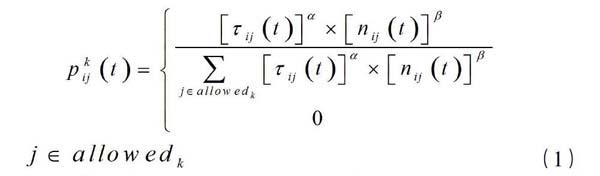


摘要:隨著人民需求的日益增長,出外旅游成了生活的一部分。但是如何規劃旅游線路節省時間使路徑最短是論文考慮的問題。文章利用matlab軟件通過蟻群算法對西安著名的16個景點進行了路徑規劃,實例證明,蟻群算法在解決路徑優化這類問題是相對有效的。
Abstract: With the increasing demand of the people, traveling abroad has become a part of life. But how to plan the travel route to save time and make the route shortest is the issue considered by the thesis. The article uses matlab software to carry out path planning on 16 famous scenic spots in Xi'an through ant colony algorithm. The example proves that the ant colony algorithm is relatively effective in solving such problems as path optimization.
關鍵詞:蟻群算法;最優路徑;matlab軟件
Key words: ant colony algorithm;optimal path;matlab software
中圖分類號:F252? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼:A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號:1006-4311(2020
0? 引言
隨著科技的發展,互聯網技術使得網上訂酒店車票非常方便,利用各類app進行查詢旅游景點相當方便,所以隨著生活水平的提高,自助游將會越來越受到人們追捧。人們會根據出行的時間合理的規劃旅游行程,選擇合適的景點個數,但是實際出行中,還會伴隨其他問題的產生,例如旅游路找的規劃、旅游費用等,這個時候需要合理的方法解決這個問題。許多學者對這個問題進行研究,最早源于TSP旅行商問題[1],隨后對該問題的算法進行深入研究,解決這類問題常用的方法有蟻群、粒子群、遺傳算法等等。論文結合蟻群算法,對陜西省著名旅游景點進行路徑規劃,蟻群算法可以為我們提供最佳的旅游順序。
1? 算法介紹
蟻群算法(Ant Colony Optimization,ACO)于1992年由Marco Dorigo提出,來源于實際生活中螞蟻尋找食物過程中發現路徑的行為,最早用來解決旅行商問題[2]。
如圖1所示,有兩條路線,ABD和ACD,其中ABD是一條直線,ACD是一條曲線,ACD長度是ABD長度的兩倍,C點是曲線ACD的中點。假設有兩只螞蟻分別為a、b,螞蟻a采取ABD路線,而螞蟻b采取ACD路線。同時從A地出發趕往D然后再回A地。當a到達D時,b正好到達C,當a從D回到A時,b正好到達D。此時殘留在ABD途徑中的激素是ACD途徑中的激素的兩倍[3]。
算法相關規則主要包括兩種:
①路徑轉移規則。
開始狀態,每只螞蟻被隨機放到其中的一個城市上,第k只螞蟻在t時刻從城市i到城市j的轉移概率為:
式(1)中,τij(t)表示t時刻路段(i,j)戶上的信息素的量,在初始時刻各條路徑上的信息量相等,即τij(0)=常數,nij(t)為啟發函數,nij(t)=■。dij表示路段(i,j)的長度。allowedk表示螞蟻可選擇的節點集,α表示軌跡相對重要性的信息啟發因子,β表示能見度相對重要性的期望啟發因子。
②軌跡更新規則。
在迭代過程中,螞蟻需要使用本地更新規則在移動的每個步驟中更新相應路徑上的信息素濃度,更新規則如式(2)所示:
式(2)中ρ表示信息索揮發系數,且ρ的取值范圍為ρ∈(0,1),由于信息素更新策略的不同,全局搜索能使我們得到更好的解決方案,因此采用如式(3)所示的全局信息索更新規則:
式(3)中,Q表示螞蟻循環一周時在一定程度積累的信息素總量Lk表示本次循環中,螞蟻k所走路段的長度[4]。
2? 實例驗證
2.1 實例介紹
陜西省是一個具有濃厚歷史韻味和人文特色的著名旅游城市,論文選取陜西省16個著名景點作為分析對象,其中包含自然景觀、歷史遺址、現代建筑等等相對具有代表性的旅游景點。其中包含秦始皇陵及兵馬俑、華清池、大雁塔、唐長安城大明宮遺址、城墻永寧門、鐘鼓樓、回民街、小雁塔、大唐芙蓉園、陜西歷史博物館、西安世博園、白鹿原、西交大(曲江)、西工大、馬嵬驛、華山等16個景點。這些景點有些分布陜西省城區,有些分布在西安市內,分布不一,如果沒有做好規劃,會造成路線的重復,這樣既浪費時間,又增大成本,因此應重點對旅游的順序進行一個簡單的排序,論文以距離最小化為求解目標,展開西安旅游景點的路徑規劃。
景點坐標如表1所示。
2.2 matlab結果分析
文章所表示的距離,是用地理坐標直接計算,換算為實際距離需乘以地球半徑,這里簡單處理,得出旅游順序即可。通過matlab結合蟻群算法,對旅游路線進行規劃迭代。
將表中的數據寫成的矩陣形式導入到MATLAB中,蟻群算法中種群數量設置與城市的個數相對應為16。根據若干次MATLAB仿真試驗結果對蟻群算法的其他參數進行設定:激素重要程度參數設置為1,啟發因子重要程度參數設置為5,激素蒸發系數設置為0.1,激素增強系數為100,最大迭代的次數設置為200,利用同樣的參數和程序對西安市旅游景點進行多次MATLAB仿真計算。最優結果如圖2所示。
最短距離:3.7215(地球半徑)
最短路徑順序:7—4—6—5—10—3—8—9—13—11—2—1—16—12—14—15—7
3? 結束語
路徑優化是實際中一個很常見的問題,在生產調度,資源優化等等問題中都有較多的應用,而論文對旅游線路的規劃也具有一定的實際意義。通過多次調整,最終實現路徑最短,迭代最快,達到我們所要實現的目標。但是論文對于實際中的費用等因素沒做考慮,今后的研究應重點針對實際影響因素,這樣蟻群算法可以更好地解決實際問題。
參考文獻:
[1]鄒臘英.基于TSP問題的旅游路線安排[J].蘭州文理學院學報(自然科學版),2015,29(05):23-25.
[2]肖艷秋,焦建強,喬東平,杜江恒,周坤.蟻群算法的基本原理及應用綜述[J].輕工科技,2018,34(03):69-72.
[3]開吉,楊金云,蔣其岑,王玉琴,開晶晶.基于蟻群算法的物流配送路徑的研究[J].物流工程與管理,2018,40(02):74-76.
[4]萬慧云,蔣艷.基于蟻群算法的5A景點旅游路線規劃問題研究[J].軟件導刊,2019,18(04):141-144.

