上行與下行人腿膝部受力問題分析

盧冠辰

(洛陽市第一高級中學，河南 洛陽 471000)

0 引言

人類下肢的結構十分精密，膝部是下肢的一個重要支撐作用集中點[2,4,7,8]。它除了承載由人體自重而產生的靜態重力作用外，運動過程中的慣性力也由膝部承擔。事實上，國際上對于腿部運動的研究是相當深入的，重視加之合理的下肢運動方式，有利于減少膝部受損情況發生的幾率。雖然相關討論眾多，但這些討論大多基于對行走式機器人相關關鍵要素的分析，對于腿部運動對應的人身基礎受力問題，現有分析并不足夠充分和深入。從現存模型上看，盡管整體機器的多連桿運動經典模型，可被應用于下肢運動研究及規律分析，然而，對于人體的下肢多樣化的運動方式及相關運動環境因素、或對于人本身面臨的下肢運動問題的分析及判斷等，在實際人腿運動受力方面，較為復雜的研究模型就顯得并不方便，也并不容易得到膝部具體受力與運動方式上的明確關聯。顯然，提出一種簡化的易于理解的下肢運動模型，并具體分析人腿膝部受力的量化問題，一方面可以得出明確的腿部運動與腿部受力間的數量關系，同時，對普及或推動下肢健康運動的認識也會形成有益的討論，而所有這些對于引發初學者的步行式機器人的入門研究也會產生一定的促進作用[1,6,9-11]。因此，本文以上下行腿部運動為研究對象進行模型簡構，并作受力分析，以期為腿部運動的受力關系及相應的膝部關節相關防護方面進行有意義的討論。(參見圖1(b))

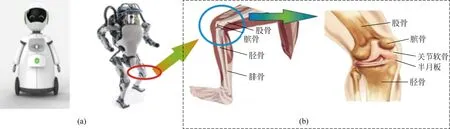
圖1機器人(a左)來自網絡(BU robot)；機器人(a右)，是已被Google的“Atlas”雙足機器人； (b)腿部關節簡圖及膝部具體結構

腿部支撐身體重力，人體通過腿部常見的肢體運動來實現身體的物理遷移。基于現代化的工具或設備使得目前人體的移動方式主要建立在滾動的運動形式上，但肢體的運動方式仍然無法被全面替代。一方面，人們出于關注健身方面問題的需要，有益的下肢運動是人們關注的熱點，另一方面，連接桿式運動在智能化社會進程發端之初也是科學家十分關注的研究課題[1,2,5,6,9-11]。(如下圖1(a)普通滾動行走機械人及行走下肢行擬人行走機械人)。

1 建模及過程分析

作為人腿行走的主要方式，上行與下行地位的重要性是顯而易見的。由于上下樓過程步長以及步高(或步深)有顯著的周期性(見圖2)，為了問題研究的方便，我們將腿部的上下行行為簡化為常見的上下樓過程，并以此為基礎進行腿部模型構建和簡化分析。

圖2 上下樓梯平衡過程真人模擬：(a)(b)上樓梯準備及模擬啟動； (c)(d)下樓梯準備及模擬啟動

在上樓過程中，前腿起人體主支撐作用，后腿輔助身體遷移至上級臺階，當前腿直立時，原后腿移至上級臺階并彎曲，此時，身體重心切換遷移至新的前腿，并完成后面腿部的直立，直到最先啟動的腿再度移動至上一臺階并發生彎曲，如此完成一個上行周期。在下樓過程中，后腿起人體主支撐作用，前腿輔助并移至下一臺階。當后腿直立時，身體重心切換移至前腿，前腿發生彎曲后直立，直到最初的后腿再度移動至下一臺階并發生彎曲，如此完成一個下行周期(見圖3)。

圖3(a) 上下行樓梯的簡圖; (b) 受力腿的彎曲及其受力圖示

從以上實際過程分析及圖示分解可以看出，上下樓梯過程是身體重心在腿部支撐作用下的曲腿直立過程，膝部是整個人體上下行的受力核心。假如在每一個移動過程中，人體均處于受力平衡或平衡運動狀態，便可以方便地將這一曲腿直立的受力過程進行簡化。如圖3(b)所示，為了保持身體平衡，身體的重心落于支撐曲腿的足部，而腿部關節的角度在可調范圍變化，其過程均滿足重心落于支撐腿足部的基本規律。有了這個基本前提，同時考慮忽略腿部自重，視腿部為輕質剛性連桿，便可簡構此過程的靜態及平衡運動模型，并在此基礎上對承力腿的受力進行過程分析。

1.1 靜態平衡上下樓受力分析

1.1.1 上樓梯的平衡受力分析

如圖4所示，依照人體重心通過提供身體支撐的前腿足部，腿部的受力處于平衡。此時，以膝關節中心部位為實際支點，大腿所受外力處于力矩平衡狀態，因此可得如下關系：

圖4(a) 上樓梯時運動模型(含相關參數); (b) 大腿、小腿分解受力; (c) 膝部受力合成； (d) 弱化膝部受力的補充力圖

(1)

如圖4中，F1為通過膝關節前端的髕骨由肌肉肌腱一體產生的沿大腿向上的拉力，F2為通過膝關節前端的髕骨由肌肉肌腱一體產生的沿小腿向下的拉力。其中作用于膝關節的切線豎直向下的力為F，F到膝關節中心的距離為L0，由于自身重力而產物的逆時針力矩為由人體在大腿上產生的力FG與力臂長LG的積，b為小腿長度，β為小腿與水平地面的夾角，M為人自身的質量，g為重加速度。因此可得：

(2)

顯然，此時，沿膝關節前方切線所受豎直向下的力由人體自重Mg、小腿長度b、小腿與水平地面夾角β、及人體重力方向到膝關節中心的距離L0共同決定。

根據力的三角形法則(圖4-Ⅲ)及余弦定律，可得如下方程：

結合方程(1)可得：

顯然，Mg、b、L0為常量，為了分析膝部受力的變化情況，可將膝部的受力作以下簡化：

(3)

其中ε為由Mg、b、及L0規定的常量。

由此可見，上樓梯時，膝部受力對于特定的人而言(小腿長b及體重Mg一定)，膝部受力主要和小腿與水平地面的夾角β，及大腿與水平臺面的夾角α有關。其中夾角β越大，膝部受到拉力越小。根據力的合成法則，而沿膝部髕骨的雙向拉力的合力隨二力的夾角的增大而減小，而這一合力的夾角θ與α及β的和成負相關的關系，因此，α及β的夾角和越大，膝部的受力越小。同時，設大腿與小腿外延長線的夾角為θ′，其角度的變化是一個容易觀察的量，由圖5中所示的幾何關系，可得到如下角度關系：

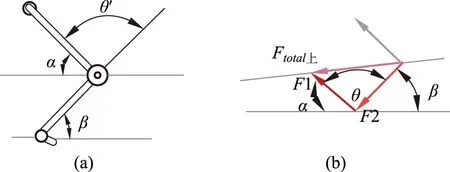
圖5(a) 重力支撐腿各方向角度關系; (b) 矢量三角形合成及對應角度關系對照圖示

而人上行時，受力腿所對應的θ′逐步變小，結合夾角β的變化，依據方程(3)，理論上可得膝部所受合力的變化情況。

上述為理論推導過程，真正要得出腿部的過程受力，還需要進行相應的實際測量。由于圖中所標注的夾角α及β隨時間變化，為了記錄其變化與時間的關系，實驗中我們采用了水平錄像的方法，將所得影像進行處理，按固定時間間隔選取圖像，以作圖軟件(Coreldraw，億圖等)對所選圖像中對應的夾角進行測量，可得如下α及β隨時間變化的圖形(如圖6所示)。由圖可知，通常情況下觀察者上樓時腿部角度按圖6所示發生變化，兩種角度的值隨時間同步增加，上樓啟動階段，以承重腿開始撐體重為起點，此時相應的兩角度均為最小值，這樣我們可以結合方程(3)以及表1中實際的腿部骨骼數據，能夠比較方便計算出正常情況下一般人群膝部受力大小以及上行時的受力變化情況。

表1 根據我國公布的成人軀干的平均數據,如表所示,確認人體各部分的長度[3]

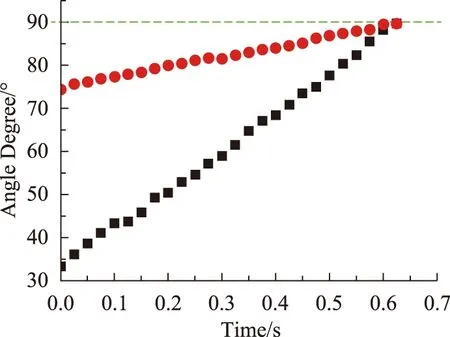
圖6 實測鴻儒小區10#樓上臺階時主支撐體重大小腿與水平面夾角隨時間變化圖(臺階平均高：156.5.mm臺階平均寬：299.0mm)：■表大腿與水平地面夾角α的度數，?表示小腿與水平地面夾角β的度數

其中，設κ為步長z的比例系數，當在上述觀測點測量時，對于同一人及相同樓梯而言，此方程可以進一步簡化，設

則可得上樓梯時，α、β兩夾角存在下列關系：

(4)

聯合上述方程(2)，(3)，(4)，結合腿各部分長度以及人體自重等已知量，便可以十分方便地計算出在靜態及平衡受力時膝部的受力情況。(過程見下圖7人上樓梯身體重心從雙足間切換至與單足垂直同線過程圖示)。依據上述結論，可以進行實際情況下的膝部受力計算及極值分析：

圖7 上臺階啟動初期臺階與腿各部長度及角度關系示意圖

1.1.2 下樓梯的平衡受力分析

如圖8所示，將人下樓梯的樣式做出簡圖，依照平衡狀態下重心通過支撐前腿足部，腿部的受力處于平衡。此時，以膝關節中心部為實際支點，求大腿處力矩平衡方程，可得：

方程中，各物理量所指均與上樓梯相同，因此我們依然可以得到以下方程：

圖8(a) 下樓梯時運動模型(含相關參數); (b) 大腿、小腿分解受力; (c) 膝部受力合成; (d) 弱化膝部受力的補充力圖示

根據力的三角形法則及余弦定律，可得如下方程：

結合方程可得：

(5)

顯然，由于Mg、b、L0為常量，故膝部的受力可簡化為：

其中ε為由Mg、b、及L0規定的常量。

同時，從圖9所示的情況來看，下樓梯也將出現與上樓梯相類似的情況，我們仍然可以得到提供支撐力的大腿與水平面夾角或小腿與足部所在平面間夾角間的關系式：

圖9 下樓梯啟動初期臺階與腿各部長度及角度關系示意圖

從上面討論的結果，可以得出結論：在參與計算的所有關系量一定的情況下，上樓與下樓腿部膝關節受力情況并無差別。兩種情況下，膝關節的受力只與大小腿與水平面的夾角有關。

2 結果與討論

2.1 實際非平衡條件下的膝關節受力擬合

前面的討論僅限于靜態或受力平衡狀態下人腿上下行的受力分析。很顯然，現實情況要繁雜的多。為了將模型的應用更接近現實，我們要做進一步討論。

現實生活及醫學證據常常證實，人們在下樓梯時膝部關節受到力要大些。從長期來看，當膝關節受力較大且持久時，造成膝關節損傷的可能性也更大。因此有人認為人們進行腿部運動時應盡量避免較多的下行活動：如上下樓時，要減少下樓運動，而生活中也有“上山容易下山難”的體驗。很顯然，實踐得出的認知從一定程度上與前本文中討論的結論出現了偏離。這主要與上面討論模型的成立以靜平衡態為前提有關。實際情況下，人在運動過程中，均會出現一定的偏離平衡態的情況，一旦整個上下行過程中出現了不平衡受力情況，相應的人腿上下行過程的受力則要在原來的模型基礎之上進行相應的條件疊加，以使其與實際情況相適應。如下圖所示，實際條件下，人的上下行過程都伴有一定的加速度，為了讓模型合理，我們應在其中引入慣性力。此時，原模型中的方程要發生相應變化：

方程中的μ為在運動中引入的豎直加速度分量，顯然，這一條件下，我們將得到一系列新的方程：

此時，我們依照實際角度來考慮上下樓梯時的區別：當下樓梯時，人的運動將伴隨著勢能轉化為動能的過程，而上樓時，這一能量轉換過程主要是人體內能轉化為人體勢能的過程。同樣條件下，下樓時身體重心將產生較大的向下慣性力(a′

據上面討論，上下行過程膝部受力方程如下：

(8)

2.2 減緩膝部受力分析

國際上通常利用腳底緩沖的方式來降低運動中膝部的損傷。例如，一般認為在塑膠材料上進行運動可以有效減少膝部損傷，該方法本質相當于減小了人體的向下慣性力。基于文中模型推導的結果，我們自然也希望本簡構模型能在上下行中膝部受力的緩解方面產生作用。

如圖10所示，從圖中我們發現，膝部所受合力的方向與運動方向大致反向(其具體方向由力的三角形合成法則決定)，如果能在圖中對膝部施加一個與此合力Ftotal相反的力Fadd，從理論上講，可以起到減弱膝部受力的效果。為了得到這樣一個力Fadd，設想在大腿與小腿間添加一個彈性物體，當大腿與水平面的夾角α以及小腿與腳部平面間的夾角β較小時，根據前面的結論，此時膝部所受合力也最大，這也是最易造成膝部受力損傷的時候。然而，與此同時，大腿與小腿間添加的彈性物體所受的壓縮形變也最大，彈性體可以產生的彈性反作用力也較大，因此，Fadd此時也應最大。兩力疊加，即可達到有效減緩膝部受力的作用效果。最終膝部的受力應為：

圖10 膝部受力及介入式減緩作用分析

F=Ftotal-Fadd

(9)

3 結論

通過上述有關上下行人腿膝部受力問題量化研究，我們可得到如下結論。

1) 從靜態或平衡運動狀態上講，人的上下行過程中，膝部受力和腿與平面的角度、小腿的長度、人的體重、樓梯的高及步長等因素有關。但由于上行與下行過程中對應的各數量因素相同，因此兩種情況下膝部受力并無區別；

2) 從上下行的實際情況上看，由于慣性力的存在，使得實際上膝部受力與平衡狀態下不同。由于上下行時兩種情況人體軀干重心產生不同的加速度，其中下行加速大于上行加速度，因此下行運動時膝部受力要明顯大于上行情況。從而用數據說明，人們認為的下行易傷膝的說法成立；

3) 文中模型可以得到上下行運動中膝部受力變化趨勢，膝部受力的極值問題也可以依具體情況可以得出。這些數據可為醫學、運動學、步行機器人的下肢構建、甚至建筑學中臺階各尺寸的合理設置等，提供有價值的參考借鑒；

4) 基于及緩解膝部受力的觀點，我們在腿部簡構受力模型中引入了附加力(詳見式(9))。從原理上有望成為一種減緩膝關節損傷的便宜方式及有效途徑；

5) 最后，文中提到的產生彈力形變的材料設計、選取、組裝，以及設置等問題將會成為本課題下一步探索的重要研究內容。