以木見林尋規(guī)律 自主發(fā)現(xiàn)促創(chuàng)新
摘 要:數(shù)學教育既要使學生掌握現(xiàn)代生活和學習中所需要的數(shù)學知識與技能,更要發(fā)揮數(shù)學在培養(yǎng)人的思維能力和創(chuàng)造能力方面的不可替代的作用。基于“發(fā)現(xiàn)”的自主探究學習,讓初中數(shù)學課堂有了新的著力點,這種以“學”為本的學習方式避開傳統(tǒng)課堂教學中只注重講解與歸納的被動式學習,讓學生主體地位得以進一步提升。
關鍵詞:發(fā)現(xiàn)歸納;自主探究;合作創(chuàng)新
中圖分類號:G633.6???????? ?文獻標識碼:A???? 文章編號:1992-7711(2020)11-074-1
教育家第斯多惠指出:“一個壞的教師奉送真理,一個好的教師則教人發(fā)現(xiàn)真理。”素質(zhì)教育和創(chuàng)新教育理念下的教師,決非僅僅是知識的傳授者,而應該把自己視為激發(fā)、鼓勵、促進學生學習和探索的引導者、促進者、咨詢者、支持者。教育面對的是人,而不是接收知識的容器。教師所做的,就是要引導學生自己去發(fā)現(xiàn),主動去學習,讓學生原有的認知基礎上,經(jīng)過觀察、探究、交流,獲得新知識或新規(guī)律。
一、從“熟視”中提練
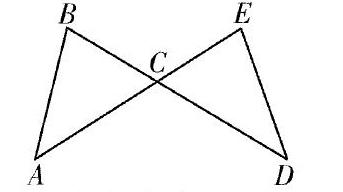
初中幾何問題中,有一類常見的基本圖形,就是由有一對對頂角的兩個三角形所構成的圖形。如圖,俗稱“蝶形圖”
(類似于蝴蝶結,也稱八字型圖,形似阿拉伯數(shù)字8),此類圖形從三角形到全選三角形,再到四邊形、相似三角形,乃至到圓的問題中,幾乎都能見到。在經(jīng)過學生自主探究之后,得出如下結論:(1)構成蝶形圖的兩個三角形有一個公共頂點,有一對對頂角,所以兩個三角形中另外兩對角的和相等,并由此進一步發(fā)現(xiàn),另外兩對角中如果有一對角相等,則第三對角也一定相等,且這一結論使用廣泛;(2)兩個三角形可能全等,也可能不全等,如果不全等,則相關結論如(1)所述,如果全等,又可分為兩種情況,一種是AB與DE平行,另一種是AB與DE不平行。
或許,學生的發(fā)現(xiàn)是淺顯的,但這畢竟只是一個開始,正如葉圣陶先生所言:“教師工作的最終目的,無非是培養(yǎng)學生具有各種良好的習慣。”相比較學生學習過程中的“被動發(fā)現(xiàn)”甚至“假發(fā)現(xiàn)”(老師直接告訴學生),這對他們“學力”的培養(yǎng)還是會起到一定促進作用。
二、在提煉中發(fā)現(xiàn)
在老師指導下,學生通過小組合作交流進一步研究發(fā)現(xiàn),“蝶形圖”在某一類幾何題中出現(xiàn)的機率非常高,這類題目特點是,在等邊(腰)三角、正方(矩)形問題中,結合全等證明,幾乎無一例外會用到這一基本圖形。而且細心的同學發(fā)現(xiàn),這個“蝶形圖”在很多時候還是解決問題的關鍵所在,往往能讓人感到“柳暗花明又一村”,令人豁然開朗。
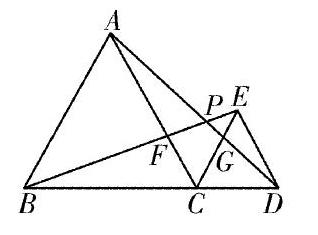
比如,已知如圖,C為線段BD上一動點(不與點B、D重合),在BD同側分別作
等邊三角形ABC和等邊三角形CDE,AD與BE交于點P,AD與CE交于點G,BE與AC交于點F,求∠APB的度數(shù).初遇這個問題時,不少學生無從下手,引導學生經(jīng)過仔細觀察分析,學生發(fā)現(xiàn)了其中的蝶形圖APFBC,結合△ACD≌△BCE可知∠CAD=∠CBE,以及對頂角∠AFP=∠BFC,很容易得到∠APF=∠BCF,從而得出問題答案。
三、由發(fā)現(xiàn)中創(chuàng)造
根據(jù)布魯納提倡的發(fā)現(xiàn)學習論,強調(diào)學生學習的靈活性、主動性和發(fā)現(xiàn)性。在教學中要求學生自己觀察、探索和實驗,發(fā)揚創(chuàng)造精神,獨立思考,改組材料,自己發(fā)現(xiàn)知識、掌握原理原則,這也是所自主探究學習所提倡的重要學習方法。強調(diào)通過發(fā)現(xiàn)學習來使學生開發(fā)智慧潛力,調(diào)節(jié)和強化學習動機,牢固掌握知識并形成創(chuàng)新的本領。“發(fā)現(xiàn)”是導向,是根本,但不是最終目的,在發(fā)現(xiàn)中創(chuàng)造,才是學習的終極目標。
通過前面案例的研究,學生已對“蝶形圖”形成相對直觀且全面,同時又具有一定理性的認識,并且在很多問題中能夠具備更加主動發(fā)現(xiàn)的意識,為相關問題的分析解決提供了有力的保證。自主探究學習在一定程度上轉變了課堂的屬性,由“教”轉為“學”的課堂,一旦學生的學習主動性得以激發(fā),其所帶來的積極效應會引發(fā)學生的更多創(chuàng)造力。
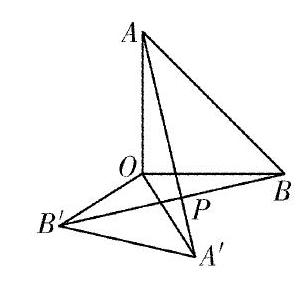
有學生在后續(xù)探索中提出,對于如圖所示的有公共直角頂點的兩個等腰直角三角形AOB與A′OB′,無論其中一個三角形如何旋轉,總能通過蝶形圖ABPB′A′證明到AA′⊥BB′。而還有學生提出,AA′與BB′的夾角大小與兩個等腰三角形的頂角有關,等等。總之,自從學生關注到“蝶形圖”之后,
在很多幾何問題分析時,學生都能有意識地去尋找這樣一個基本圖形,并以此為突破口,對問題進行更加深入的思考,同時,受此影響,學生在另一個常見基本圖形“一線三等角”(K型圖)問題的研究上,也更加有效。
四、教后啟示思考
基于“發(fā)現(xiàn)”的自主探究學習,讓初中數(shù)學課堂有了新的著力點,這種以“學”為本的學習方式避開傳統(tǒng)課堂教學中只注重講解與歸納的被動式學習,讓學生主體地位得以進一步提升。數(shù)學教育既要使學生掌握現(xiàn)代生活和學習中所需要的數(shù)學知識與技能,更要發(fā)揮數(shù)學在培養(yǎng)人的思維能力和創(chuàng)造能力方面的不可替代的作用。培養(yǎng)學生的歸納總結能力,也是數(shù)學教學中不可或缺的內(nèi)容之一。以木見林,才能拓展學生視野,有了歸納,才能形成自己見的,再談創(chuàng)新方有可能。通過“發(fā)現(xiàn)”,可以讓不同的學生在多層次、全方位的各個角度體驗學習的樂趣,使學生以更主動的學習狀態(tài),積極投入,熱情參與,從而使學生的創(chuàng)新精神和生命潛能得到充分發(fā)揮,這也正是初中數(shù)學教育的根本追求。
[參考文獻]
[1]吳鋒.基于“發(fā)現(xiàn)”的初中數(shù)學導引式合作學習[J].中小學數(shù)學,2016(1-2).
(作者單位:南通市通州區(qū)實驗中學,江蘇 南通226000)

