借助“雞兔同籠”思想理解并運用十字交叉法

劉紀偉

摘要：“十字交叉法”是化學計算中廣泛使用的解題方法之一，它具有形象、直觀并且簡潔的特點。但是往往學生不容易理解使用這種方法解題的原理。本文從我國古代名題“雞兔同籠”問題出發分析“十字交叉法”的原理并加以運用。

關鍵詞：雞兔同籠;十字交叉法

中圖分類號：G634.8 文獻標識碼：A文章編號：1992-7711（2020）12-087-1

一、原理分析

“雞兔同籠”問題是小學奧數的常見題型。其中，《孫子算經》為我們提供了一種解題思路：先將94÷2=47（可以理解為先把雞和兔各砍掉一半的腿，此時雞剩一條腿，兔剩2條腿），再用47-35=12（即多出來的腿是兔腿）便可得到兔的數目，最后用35-12=23便可得到雞的數目。該解法最重要的思想是抓住雞腿和兔腿的差量，而每只雞的雞頭和每只兔的兔頭數目是一樣多的，所以利用差量除以2即可得出兔子數目。

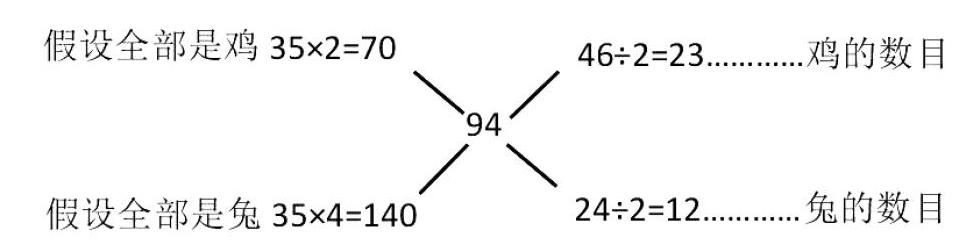
若將此思想融入十字交叉法中，則可以利用假設法，作出十字交叉圖，具體思路如下。假設兔和雞一樣只有兩條腿，則一共70條腿。可是籠中有94條腿，多出了24條。這多出的24條實際上是兔多出來的，因為一開始把兔假設成兩條腿，所以每只兔少算了兩條腿，那么用24÷2=12，便可得兔的數目，畫圖如下：

同理，假設雞和兔一樣有四條腿，則一共140條腿。可是籠中只有94條腿，少了46條。這少了的46條實際上是雞少的，因為一開始把雞假設成四條腿，所以每只雞多算了兩條腿，那么用46÷2=23，便可得雞的數目，畫圖如下：

將兩圖合并即可得十字交叉圖：

借助雞兔同籠思想理解并運用十字交叉法，是一個直接的思維過程。學生只要在題目中找到對應的假設對象，并找到假設后的某一參數與原題中對應的參數有差值，則可以利用差值來畫出十字交叉圖。

二、運用舉例

現以下題為例，說明雞兔同籠思想的運用：

一個密閉容器中，中間有一可自由滑動的隔板，將容器分成兩部分.當左邊充入1 mol N2，右邊充入8 g CO和CO2的混合氣體時，隔板處于如圖所示位置（兩側溫度相同）。則混合氣體中CO和CO2的分子個數比為（ ）

A.1︰1 B.1︰3 C.2︰1 D.3︰1

首先，利用阿伏伽德羅定律推出右邊氣體物質的量為 0.25mol，再根據平均摩爾質量的定義算出=8 g/0.25 mol=32 g/mol。假設氣體均為CO（分子量28），則多了4 g/mol;假設氣體均為CO2（分子量44），則少了12 g/mol。而實際上每摩爾CO和CO2的質量差為16 g/mol，則可以具體算出1 mol混合氣體中CO和CO2的物質的量

即可得每摩爾混合氣體中兩者的含量。當混合氣體變為0.25 mol時，則從上面的數再除以4，即n（CO）=0.75÷4=0.1875 mol，n（CO2）=0.25÷4=0.0625 mol。

通過以上例題學生能更好的理解并掌握運用十字交叉法，理解了十字交叉法后對拓寬學生的解題思維，提高學生創新能力都具有良好效果，這比純粹地用十字交叉法解題更有助于學生對化學問題的理解。

[參考文獻]

[1]滕湘文.妙用十字交叉法解決化學計算問題[J].中學化學教學參考，2014（18）：68.

[2]王佳瑩.小學奧數與中學方程——以雞兔同籠為例[J].數學學習與研究，2017（19）：118.

（作者單位：廣東省中山市中山紀念中學，廣東 中山 528454）