基于感性具體到理性抽象再到理性具體的教學
——“等差數列的前n項和”課堂教學片段與點評*

徐德均

(江蘇省南通中學 226001)

所謂抽象，是指在認識上把事物的規定、屬性、關系從原來有機聯系的整體中孤立地抽取出來；而具體是指尚未經過這種抽象的感性對象，就是實實在在的．馬克思認為人對客觀事物的認識是在實踐的基礎上，由感性的具體上升為理性的抽象，進而把各種抽象的規定通過更深刻的思維加工，達到具體的再生產，由理性的抽象上升到理性的具體，從而把握事物的內在聯系和本質的過程．

“等差數列的前n項和”是高中數學必修5 (蘇教版)第2章第2節“等差數列”的第3課時，主要包含用“倒序相加法”推導等差數列的前n項和的兩個公式，結合通項公式揭示五個基本量的“知三求二”的思想方法．它既是前段學習的等差數列的概念、通項公式等知識內容的延伸、鞏固和應用，也是進一步學習后續其他知識的基礎，更是為用類比的方法學習等比數列作了鋪墊，無論在知識層面還是能力層面上，都起到了承上啟下的重要作用．

本文結合2019年江蘇省中學青年數學教師優秀課觀摩與評比活動中，筆者指導的一位青年教師以“等差數列的前n項和”為課題獲一等獎的課堂教學片段，簡述由具體到抽象，再由抽象上升到具體的教學與點評．

1 基于感性的具體到理性的抽象，講述歷史典故引入課題

·教學片斷1

師：我國古代數學巨著《九章算術》中有這樣一個故事:今有良馬與駑馬發長安至齊，齊去長安三千里．良馬初日行一百九十三里，日增十三里……故事中，有同學們熟悉的數學知識嗎?

生1：根據等差數列的定義，良馬的逐日行程數193,206,219,…，是一個以首項為193、公差為13的等差數列．

師：對！還可知道，良馬每日的行程數，如第15日的行程數為193+(15-1)×13=375．根據你的生活經驗，就這則故事中的良馬問題，還想知道或研究什么？

生2：想知道良馬的日行程和，如前15天良馬總共走了多少路程？

師：很好！這是一個值得研究的問題，就是我們今天要研究學習的等差數列的前n項和Sn．(教師板書課題：等差數列的前n項和)

點評從講述《九章算術》中歷史數學故事開始，借助于感性具體的良馬問題，引導發現良馬問題中蘊涵著熟悉的等差數列等理性的抽象，將探求前15天良馬日行程總和的具體實際，抽象為探求等差數列前n項和的理性問題，既回顧等差數列的定義、通項公式等舊知，又引發新的課題，設計巧妙自然，具有數學史、傳統文化傳承教育之意義．

2 基于感性的具體到理性的抽象，將不等轉化為相等求和

·教學片斷2

師：如何求良馬前15日行程的總和S15．

生3：將良馬前15日行程數逐個相加求和．

師：可以！好像繁冗了點．

師：這方法可以！但你知道高斯如何得到這種求和方法的嗎？(學生集體沉思)其實，早在高斯之前500多年，我國古代數學家楊輝在《詳解九章算法》書影中，給出了良馬前15天行程總和的一種求和方法．圖1中是用條形圖表示良馬每日的行程，每一個條形的長度表示良馬每日的行程數，第1天的行程數用長為193的條形表示，第2天的行程數用長為193+13=206的條形表示，……依此類推，第15天的行程數用長為375的條形表示(圖2)．

圖1 圖2

將圖2中的“條形”合拼得圖3，15個條形的長度之和則為S15．那么，如何利用圖3求S15呢？請學生利用分發的“良馬圖”，小組討論，合作探究、展示求S15的方法．

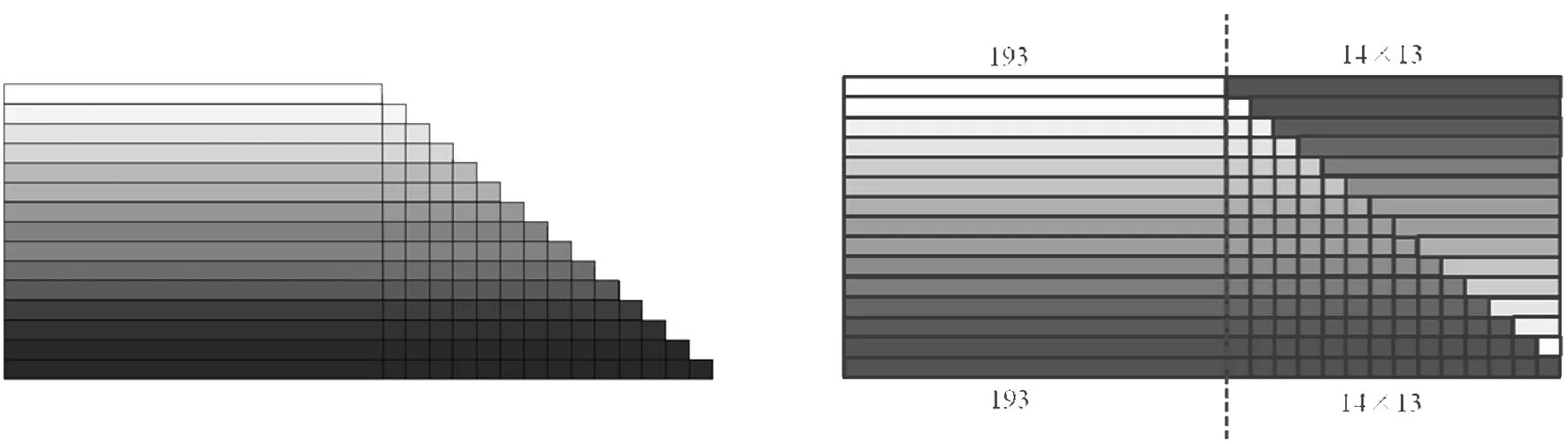
圖3 圖4

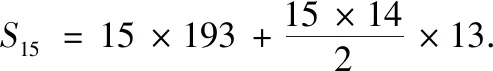
師：(通過動畫展示先“割”，再“倒”，再“補”的過程)這種求和的方法就是楊輝在《詳解九章算法》書影中給出的方法，圖3為圖1的橫向表示．

圖5

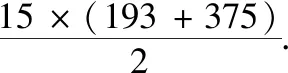
師：這組同學是將“良馬圖”整體先“倒”過來，然后再“補”上去，得到15個長度都為193+375的條形，是將“不等行程數”的求和轉化成“相等行程數”倍數，達到求S15之目的．這種方法就是前面一位同學所說的數學家高斯的求和方法．

點評借助于我國古代數學家楊輝將“良馬圖”先“倒”再“補”通過幾何直觀求S15的思路，理性抽象出將“不等行程數”轉化成“相等行程數”的倒序求和，這是從圖形、數量關系中抽象的過程，也是發現“倒序求和”的數學思想方法的思維過程，更是一個沿著古人發現的足跡、傳承歷史先人們智慧的教育過程．

3 基于感性的具體到理性的抽象，歸納推證前n項和公式

·教學片斷3

師：能利用“良馬圖”的幾何求和的思想，推證等差數列{an}的前n項和公式嗎？

生6：可以！設等差數列{an}的首項為a1，公差為d，則等差數列{an}的前n項和Sn=a1+a2+…+an=a1+(a1+d)+…+[a1+(n-1)d]．同時Sn=an+an-1+…+a1=an+(an-d)+…+[an-(n-1)d]．兩式相加，得2Sn= (a1+an) + (a1+an) + … + (a1+an) =n(a1+an)， 由此可得等差數列{an}的前n項和公式Sn=

圖6

師：說說為什么有如此的想法？

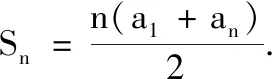
師：很好！這樣我們就得到等差數列{an}的兩個前n項和公式，這兩個求和公式可以用通項公式聯系起來．

點評由“良馬圖”的先“倒”再“拼”幾何直觀求和，類比到代數中先“倒序”再“相加”，推證等差數列{an}的兩個前n項和公式．從解決問題的思想看這是一致的，都用了“倒”的方法．

4 基于理性的抽象到理性的具體：應用求和公式知三求二

·教學片斷4

例1請填寫有關等差數列{an}的表格：

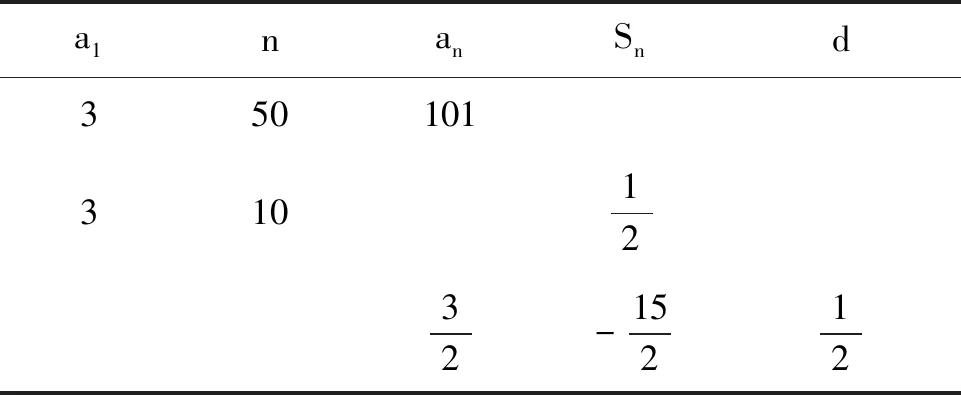
a1nanSnd3501013101232-15212

(師生集體分析與學生個性自主練習，教師黑板板書，解答填表)

師：根據等差數列{an}的兩個前n項和公式，可建立關于a1,d,n,an,Sn這五個基本量的兩個等式關系，較好地完成求解填表，很好！還有更進一步的感悟嗎？說明理由．

生8：在等差數列{an}的a1,d,n,an,Sn這五個基本量中，已知其中三個，就可以求余下的兩個——“知三求二”．因為雖然五個基本量有三個公式，可以列三個等式，但其實僅是兩個“獨立等式關系”，即只有兩個獨立的方程，所以已知其中的三個量，便能求得余下的兩個量．

師：說得很好，也很到位！現在請同學們再看一道題．

例2在等差數列{an}中，已知前10項的和為310，前20項的和為1 220，求前30項的和．

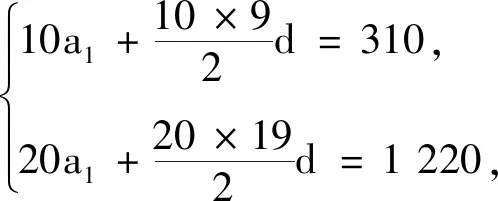
師：若將題變為：(1)在等差數列{an}中，已知第1項到第10項的和為310，第11項到第20項的和為910，求第21項到第30項的和．請用兩種方法求解．

(2)請課后查閱、研究《九章算術》中這則有關良馬的完整故事．

點評等差數列的兩個前n項和公式是理性抽象的結果，而“知三求二”則是理性應用，是運用理性抽象的結果解決具體問題總結而得的規律，也是函數與方程思想在數列問題中的理性運用．

5 總結

2017版普通高中數學課程標準提出：數學抽象是指通過對數量關系與空間形式的抽象，得到數學研究對象的素養．它反映了數學的本質特征，貫穿在數學產生、發展、應用的過程中．

上述幾個課堂教學片斷正是循著古人的足跡，從《九章算術》中一則故事出發，引入學習與研究的課題，將探求的幾何直觀求和類比到代數中的倒序求和，歸納推證等差數列的兩個前n項和公式，舉例歸納“知三求二”思想的應用與鞏固．呈現出的是能從歷史故事等情境中抽象出數學概念、命題、方法和體系，是從感性具體到理性抽象的活動經驗積累，也是在日常生活和實踐中一般性思考問題習慣的養成，更是把握事物的本質，從感性的具體到理性的抽象，再從理性的抽象上升到理性具體的以簡馭繁．