蘇教版2019版教材習題的“變”與“不變”
——以“集合”一章為例*

丁益民

(江蘇省蘇州實驗中學 215011)

2019版蘇教版《普通高中教科書·數學》[1](下稱新教材)經過多年的編制、試教、調整，于2019年獲得教育部審定通過并開始投入使用．新教材與2004版蘇教版教材(下稱舊教材)相比，在體系上發生了較大變化，在新課改中對新教材進行研究很有現實意義．

習題作為教材的重要組成部分，起著鞏固新知、培養技能、促進理解和發展思維的作用．新教材在習題的呈現方式上繼續沿用了舊教材的編寫格式，設有“練習”“習題”“復習題”等欄目．整體而言，習題的數量、素材、難度等方面既有保留舊教材傳統的方面，也有對舊教材習題進行調整的地方．本文擬以必修第1冊“集合”一章為例談談新教材的變與不變，以期拋磚引玉．

1 從習題數量看教材編寫的穩定性

作為初高中銜接的起始章節，本章的教學知識并沒有變化，均含有三節內容，習題數量變化不大，其中新教材習題的總數為60道，而舊教材習題的總數為55道(注：統計時均以大題號為準，有多個小題的以一道大題計)，具體分布如下：

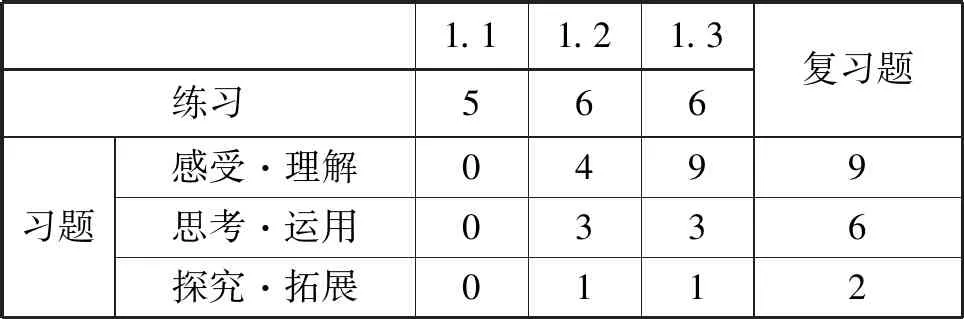
表1 2004版“集合”習題分布

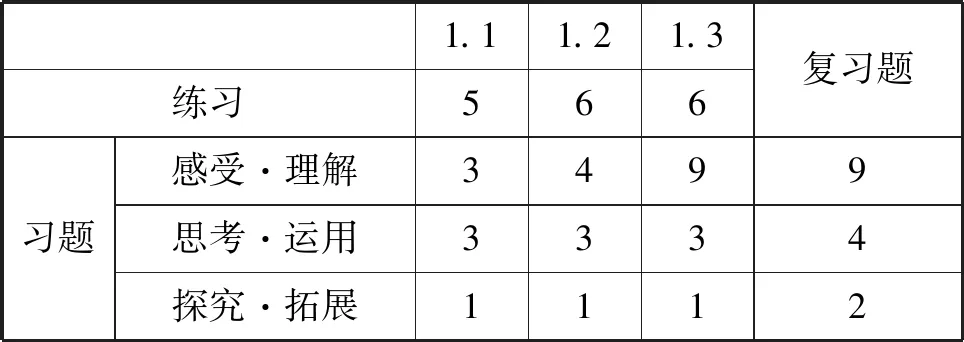
表2 2019版“集合”習題分布

從表中可以看出，各節的“練習”“習題1.2”和“習題1.3”的題量保持不變，而“習題1.1”的數量由0增加到7道；“復習題”減少2道．盡管“練習”的總數保持不變，但個別題目進行了增減與調整.如新教材中1.1節“練習”的第4題為新增題目，而舊教材中的第5題被調至本節習題的“思考·運用”，這是基于練習是單純理解概念的考慮．再如1.2節“練習”的第6題也是新增題目，這是由于舊教材的第6題屬于理解運用的范疇．“習題1.2”第5題、第8題以及“習題1.3”第8題分別取代舊教材同位置題目．復習題絕大多數題目沒有變化，只是刪除了舊教材復習題中的第11題和第17題．值得注意的是，舊教材1.1節沒有配設相應習題，使得新教材在編寫該節“習題”時除第4題外其余6道題均為新增題目(注：第3題第(2)小題為舊教材此節練習的第2題第(4)小題)，第4題則是原練習第3題的(2)～(4)．

不難看出，與舊教材相比，新教材習題的數量基本保持穩定，習題的數量能夠保證不同水平的學生在學習知識時進行概念的鞏固、理解與訓練．同時，數量的穩定性給新課改的實施提供了一個比較好的緩沖度，特別是一線教師如何把控教學要求和教學難度能得到保證．

2 從習題的變化看教材編寫的科學性

通過兩版教材的比較，發現新教材對舊教材中的部分習題作了必要的調整和替換，主要包括習題位置的調整、習題的表述方式的微調、習題的增加與刪除等．從這些變化中可以看出教材習題的選擇與編排更具有典型性和實用性，更符合學生學習的心理規律．按照數學運用的不同層次，習題可以分為[2]：辨認識別、變式練習、解決簡單問題、解決復雜問題等．選配比較典型的題目，使得它們內部自成系統、相互聯系．另外，選取的素材與時俱進，更符合培養當代公民素養的要求．習題的設置也更具有層次性、思維性，有利于學生的思維發展和素養提升．

2.1 習題的定位更加合理

練習主要是及時鞏固課堂知識，進行辨認識別的同化順應活動，當然其中也會有少量的變式練習，題目更多地關注知識與技能的認識與鞏固，因此不宜出現高于學生認知起點的題目.按此原則編者對舊教材的部分習題作了更合理的調整．如舊教材1.1節“練習”中第2題的第(4)小題和第4題的第(2)小題均屬“點集”，而“點集”的學習要求明顯高于學生的認知基礎，學生需要進一步理解集合概念的本質后再進行認知．因此，在新教材中這兩道題均調整至習題的“感受·理解”部分，調整之后更符合學生的認知規律，也有助于學生對集合本質的理解．

習題和復習題的題目均以“感受·理解”“思考·運用”“探究·拓展”三個維度呈現，三個維度代表著思維層次的不斷遞增[2]：“感受·理解”比練習要求稍高一些，學生要進行一些操作性活動，靈活運用所學知識解決問題；“思考·運用”比“感受·理解”的思維層次更高，要求學生通過深入的思考，運用所學知識解決問題；而“探究·拓展”主要著眼于鼓勵學生進行探究與創造性思維活動，所選素材也更具有探究性、創造性、開放性．編者根據舊教材使用的實際情況對部分習題的位置進行了調整．如舊教材復習題第13題是探究集合A,B,A∪B中元素的個數可能存在的關系(本質是容斥原理)，此題具有探究性，思維層次較高．為此，新教材將此題調整至“探究·拓展”欄目.調整后更符合題目的思維定位，也更貼近學生認知的心理規律．

2.2 習題的功能更加豐富

除了題目順序的調整外，新教材還對舊教材部分題目進行了增減，增加的題目充分考慮題目的教學功能．比如1.1節“練習”第5題增加“漢字‘永’的筆畫組成的集合”與上面的“‘mathematics’中的字母構成的集合”形成中英文互補，使素材更加豐富飽滿，學生對集合中元素屬性的理解也更全面．“習題1.2”第8題為新增題目，引導學生從子集符號“?”與不等號“≤”的結構相似性中去發現符號“?”的性質，旨在培養學生的類比思維，準確理解子集的內涵．另外，題目背景的設置也更具有時代特色，如“習題1.3”第8題融入現代生活中的微信群，而且設置的群成員有中國傳統文化中的“梅蘭竹菊”，讓學生更親切地感受到教材素材與時俱進的中國文化屬性．

2.3 習題的表述更加嚴謹

新教材對舊教材中部分習題的表述更加嚴謹到位．如“習題1.1”第5題，原表述為：

“設M={1,2}，N={a,b}，若M=N，求實數a,b的值．”

調整后為：“設a,b為實數，已知M={1,2}，N={a,b}，且M=N，求a,b的值．

將a,b的論域前置，與必修第2冊“復數”的引入協調統一，體現數學語言的嚴謹性和整體性．像這樣的調整在新教材中有很多，再比如“習題1.2”第7題將“求實數m的值”調整為“設m為實數……求m的值”等．

3 從習題的設置談教材教學功能的開發

長期以來，有些教師不注意對教材習題的研究，把教材習題僅僅作為隨堂練習或課后作業布置給學生，缺少對習題的挖掘與整合，忽視了對習題教學功能的開發，使得習題的功能單一化、淺表化，教材意圖不能凸顯．事實上，教材中的習題往往有著深刻的編寫意圖，要通過研究發掘習題本應有的教學價值，特別是促進學生對數學本質的理解和提煉思維訓練的要素．

3.1 設置持續化的學習活動

教材在編寫中充分考慮學習活動的連續性，通過在每一小節都設置同一知識相關的問題，以期達到促使學生對其產生持續的思考．如第8頁練習第3題[3]：

用描述法表示下列集合：(1)奇數的集合；(2)正偶數的集合．

第11頁練習第4題：

若U=Z，A={x|x=2k,k∈Z}，B={x|x=2k+1,k∈Z}，則UA=，UB=．

第14頁練習第6題：

設A={x|x=2k-1,k∈Z}，B={x|x=2k,k∈Z}，求A．

教材并不是簡單地重復奇、偶數集，而是從最樸素的自然語言出發，逐步地將其過渡到符號語言，再轉變為形異質同的符號語言．教學實際中，學生對整數劃分比較缺乏經驗，教材對整數集Z進行奇偶分類，是最簡單、最特殊的一種劃分方式，這其中也是給學生提供對整數集Z按照“剩余類”進行劃分的經驗范式．

3.2 引導進行完整的數學抽象活動

數學抽象[4]是數學的基本思想，是形成理性思維的重要基礎，反映了數學的本質特征．數學教學應讓學生經歷完整的抽象過程、參與完整的抽象活動，學生的數學抽象素養是在抽象過程中逐步孕育的，并且只有完整的抽象過程、抽象活動才能培養出完整的抽象能力和抽象素養．因此，數學教學應再現和強化抽象的過程．教材有意識地在相關習題中滲透完整的抽象過程，引導學生經歷完整的抽象活動．如第16頁第10題：

(1)U={1,2,3,4,5,6}，A={2,3,5}，B={1,4}，求U(A∪B)與(UA)∩(UB)；

(3)由(1)(2)，你發現什么？

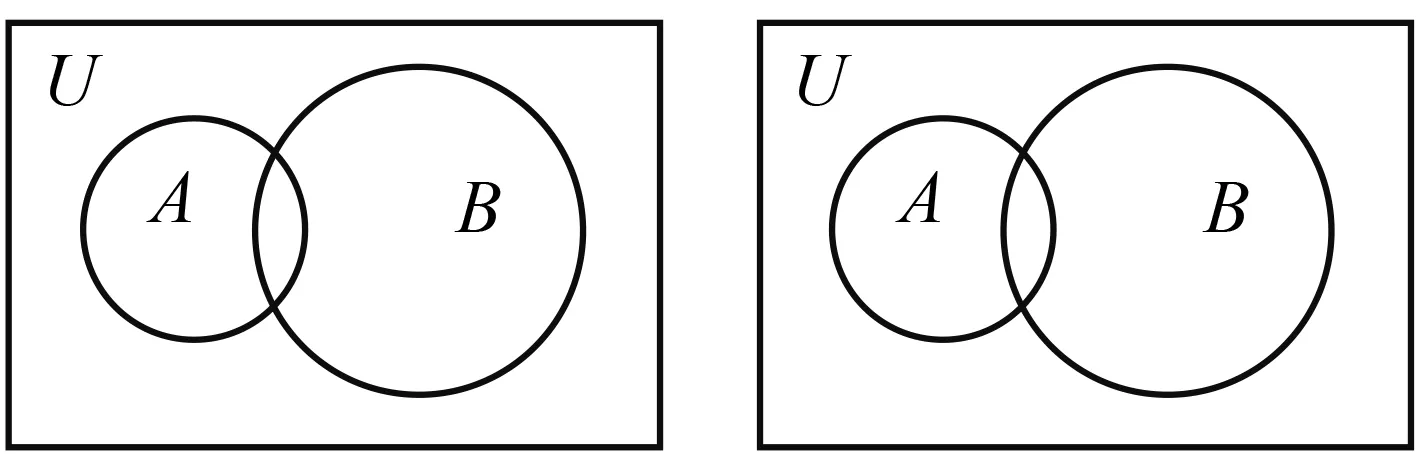
圖1

第20頁第12題：

這兩題揭示的是邏輯學定律——德·摩根定律.由于高一學生的認知力決定了要經歷一系列具體的抽象活動才能認識到知識的內涵,為此教材引導學生從具體的數與數的關系、到形象的圖形與圖形的關系中抽象出集合與集合的關系．像這樣從具體背景中抽象出一般規律和結構是有利于學生進行數學抽象訓練的，更利于他們在學習中學會用集合語言進行表征的經驗積累．

3.3 多策并舉指向于探究能力的培養

新教材加強了探究性、創新性題目的設置，頗具特色的有寫作題、閱讀題、探究題等．關于數學寫作，胡耀華認為[5]：數學寫作可以幫助學生建構數學知識，有效地促進學生對數學的理解；數學寫作可以幫助學生提高“元認知”水平，提高學生解決數學問題的能力；數學寫作可以幫助學生形成良好的認知情感；數學寫作對發展學生創造性思維和批判性思維、形成數學思想有一定的價值．因此，在新教材中設置了適合學生認知特點的寫作題，比如“習題1.1”的第7題——“寫一篇關于符號‘∈’的短文”.此題旨在引導學生理解集合中的符號語言，通過搜集相關史料素材進行自我的感悟、認知與理解，給學生提供更廣闊的認知空間和更豐富的認知途徑．

數學探究是課改的重要話題，如何將它落實到課堂教學中一直是數學教學中值得探索的課題．通過數學探究，學生不僅獲得數學知識，還將經歷數學知識形成所必要的數學發現、數學分析和數學演繹，使得數學教材既有數學傳授又有數學發現，有利于學生數學素養的形成．新教材沿襲了舊教材的編寫方式，專門設置“探究題”“閱讀題”以及“探究·拓展”來引導教學方式的變化．如新教材第16頁“習題1.3”第13題定義“差集”的探究題和第20頁復習題第15題定義“A×B”的閱讀題，這些題目的設置都是為學生提供多層次、多種類的選擇，引導學生進行探究活動．通過“集合”一章的學習，學生能體會到集合之間的運算有“交集”“并集”及其混合運算，應自然地提出問題：集合之間是否還有其他運算？通過探究題、閱讀題的引領，提供認知的途徑，積累相關活動經驗，為后面學習向量、復數等的運算提供示范．

總之，對新教材的研讀，要能從內容的設置體會編寫的意圖，只有真正理解了教材，才能提高教材的使用價值和教學功能，才能真正做到“用教材教”．