探索微專題教學(xué) 提高課堂精準(zhǔn)度
——以“形如條件的應(yīng)用”為例

周秋斕

(浙江省湖州市雙林中學(xué) 313000)

1 設(shè)計背景

平面向量是有效溝通代數(shù)和幾何的橋梁，向量也是人們解決數(shù)學(xué)問題的一種重要數(shù)學(xué)工具.在高考數(shù)學(xué)中向量既是一個必考知識點，也是一個創(chuàng)新命題的切入點，常考常新.而且在近幾年的考題中，對知識的綜合性和靈活性考查增強，難度相應(yīng)有所提升.因此，教師在指導(dǎo)學(xué)生對平面向量進(jìn)行復(fù)習(xí)時，要重視回歸教材，指導(dǎo)學(xué)生對教材中向量的定理、例題、習(xí)題展開適當(dāng)?shù)奶骄颗c思考，以拓展知識和能力.其中從平面向量基本定理探究出的向量等和線就是一個重要例子，利用向量等和線求解向量線性運算中系數(shù)和問題，比建系轉(zhuǎn)化為代數(shù)問題求解更顯自然和流暢，有效降低了知識綜合性要求與運算能力要求．

2 教學(xué)過程

2.1 引例點撥

圖1

生1：建系，扇形是圓的一部分，x+y是線性關(guān)系，用直線和圓的一部分相交求解.

師：這種方法非常不錯，建系是解決向量問題的一種常用方法.

生2：還可以由圓到三角函數(shù)，將x+y轉(zhuǎn)化為∠AOC的三角函數(shù).

師：轉(zhuǎn)化為三角函數(shù)也是非常精彩的一種解法，求三角函數(shù)的最值我們還可采用求導(dǎo)方法.

生3：記OC與AB交點為D，用兩次三點共線，找到兩次等量關(guān)系.

教學(xué)反思通過引例讓學(xué)生體會不同方法的優(yōu)劣，開拓學(xué)生的發(fā)散思維，完善學(xué)生的數(shù)學(xué)認(rèn)知結(jié)構(gòu)，提高學(xué)生解決問題和分析問題的能力.

2.2 追本溯源

圖2

推論 ①當(dāng)?shù)群途€A1B1在點O和直線AB之間時，k∈(0,1)；②當(dāng)直線AB在點O和等和線A1B1之間時，k∈(1,+∞)；③當(dāng)?shù)群途€A1B1在點O上時，k=0；④當(dāng)?shù)群途€A1B1和直線AB在點O兩側(cè)時，k<0.

教學(xué)反思等和線是平面向量三點共線的擴(kuò)展，并沒有增加知識，它不過是共線定理和向量平行相結(jié)合的簡單推論，將復(fù)雜的范圍問題轉(zhuǎn)化為圖形關(guān)系問題,將具體的代數(shù)式的運算轉(zhuǎn)換為距離的比例關(guān)系，非常直觀地體現(xiàn)了數(shù)形結(jié)合的數(shù)學(xué)思想．

2.3 思維萌芽

下面通過一個例題來內(nèi)化等和線的概念.

圖3

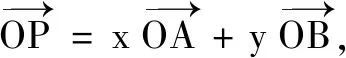
生1：我發(fā)現(xiàn)點P在直線AB上時，由共線定理可知x+y=1，故可以先將選項A排除.

生2：結(jié)合圖形，再利用等和線定理不難發(fā)現(xiàn)，等和線在點O和直線AB之間，所以x+y∈(0,1)，排除選項B,D，故答案選C.

師：等和線其實就是過點P與直線AB平行的直線，同學(xué)們對此概念理解得非常到位，再接再厲哦！

教學(xué)反思概念的初步認(rèn)知需要典型的例題加以深化，通過講練結(jié)合，體會概念的形成與運用，學(xué)生才能真正理解，并內(nèi)化進(jìn)自己的知識模塊.

2.4 能力提升

題型1 求共起點向量線性運算的系數(shù)和

生1：我們可以先找出過點P與BD平行的等和線l，而點P在圓上，等和線應(yīng)該與圓有交點，則λ+μ=k.

師：非常好，利用等和線定理，借助數(shù)形結(jié)合的思想，我們可以更快速地找到解題思路.

圖4

師：這位兩位同學(xué)快速找準(zhǔn)了解題目標(biāo)，而且利用幾何圖形知識秒殺了此題，解得非常漂亮！

題型2 求非共起點向量線性運算的系數(shù)和

高中階段所學(xué)向量均為自由向量，向量平移后得到相等向量，所以在用等和線求解問題時，平面向量共線定理表達(dá)式中的三個向量的起點一致，若兩向量的起點不同，可以將向量平移實現(xiàn)起點重合．

圖5

師：這位同學(xué)利用了等和線定理中共起點的特征，再結(jié)合圖形的特點把一道高考題秒殺了.

題型3 求向量線性運算系數(shù)的線性關(guān)系式

有時候所要求解的量是系數(shù)的一般線性關(guān)系式，而非系數(shù)和，考慮到可以通過數(shù)乘運算將向量進(jìn)行同向或者反向伸長、壓縮，所以從理論上講， 所有系數(shù)的線性關(guān)系式都可以通過改變向量的基底，將所求系數(shù)的線性關(guān)系式變?yōu)閮蓚€新的基向量的系數(shù)和．

圖6

師：同學(xué)們可以發(fā)現(xiàn)x+4y并不是所知基底向量的系數(shù)和，所以不能直接用等和線定理.那么，我們可以怎樣轉(zhuǎn)化呢？

題型4 求基底為變化向量的系數(shù)線性系式

當(dāng)基向量的終點是變化的，使系數(shù)和λ+μ=1的等和線也是變化的，所以滿足條件的等和線也相應(yīng)保持平行變化，從而求解問題的關(guān)鍵在于探求保持平行變化中滿足條件的等和線位置．

圖7

生：當(dāng)點P在EQ與半圓切點時，系數(shù)和最小，最小值為1.

教學(xué)反思向量的等和線巧妙地將代數(shù)問題轉(zhuǎn)化為圖形關(guān)系問題，將系數(shù)和的代數(shù)式運算轉(zhuǎn)化為了距離的比例運算，數(shù)形結(jié)合思想得到了有效直接的體現(xiàn)．向量的等和線法將復(fù)雜的不等式問題、范圍問題、數(shù)量積問題轉(zhuǎn)化為簡單、直接、操作方便的點到直線距離問題，很多時候用相似即可迅速解決，既提高了做題時間效率和正確率，又提升了學(xué)生的學(xué)習(xí)熱情和學(xué)習(xí)興趣，還提高了課堂教學(xué)的有效性和精準(zhǔn)度.

2.5 陌上花開

事實上，對于平面向量基本定理系數(shù)問題，與向量等和線相對應(yīng)的還有等差線、等積線、等商線和等平方和線等.如果進(jìn)一步把平面向量推廣到空間向量，則可以產(chǎn)生等和面.

圖8

圖9

圖10

2.6 課堂小結(jié)(略)

3 教學(xué)反思

數(shù)學(xué)家波利亞說過：“良好的組織使得所提供的知識容易用上，這甚至比知識的廣泛更為重要，至少在有些情況下，知識太多可能反而成了累贅，它可能會妨礙解題者去看出一條簡單的途徑，而良好的組織則有利而無弊.”既然我們能將不同的問題作為一個專題集中起來進(jìn)行復(fù)習(xí)，那么這些問題之間必然存在內(nèi)在的聯(lián)系，解決問題的方法也必定存在某種統(tǒng)一性.因此，我們要把握好微專題教學(xué)，提高課堂教學(xué)精準(zhǔn)度，就必須要做到以下幾點.

(2)構(gòu)“路線圖”，促完整性.微專題復(fù)習(xí)課的重點應(yīng)放在讓學(xué)生生成解決本專題問題的基本“路線圖”及專題所反映的一般數(shù)學(xué)思想方法上，而不只是關(guān)注單個題目的具體解法.要防止復(fù)習(xí)的碎片化，避免就題論題.將專題教學(xué)異化為同類題的綜合訓(xùn)練，起不到專題復(fù)習(xí)的效果.

(3)講練結(jié)合，注重感悟.在微專題教學(xué)中，提升學(xué)生思維能力的重要路徑是通過講解、練習(xí)引導(dǎo)學(xué)生對認(rèn)知結(jié)構(gòu)中已有的一些解法進(jìn)行反思與提煉，讓學(xué)生認(rèn)識到知識方法之間的聯(lián)系，從而幫助學(xué)生感悟技巧，建立起對一類問題的整體認(rèn)知，進(jìn)而生成處理一類問題的基本方法.這樣才能讓學(xué)生做到舉一反三，觸類旁通.