解三角形中一類問題模型的求解思路探析

馬孟華

(云南省下關第一中學 云南省高中數學張勇名師工作坊 671000)

解三角形作為高考重點考查的內容之一，主要要求考生通過對任意三角形邊角關系的探索,掌握正弦定理、余弦定理、三角形的面積公式等,并借助三角函數中的相關公式加以綜合與運算,包括解決一些簡單三角形的度量問題及一些與測量和計算有關的實際問題等.解三角形與三角函數知識大多運算量大、公式應用多,這就要求考生不僅要具有較高的運算能力、較強的應變能力和較好的記憶能力,還要善于分析與總結,形成解決此類問題的系統方法.實際上這類題型在高考中不僅具備選拔功能，而且對考生的數學核心素養提出了較高的要求，也就倒逼教師在課堂教學中應該重視和強化對解三角形問題的處理和系統認識，從而提升學生的應變能力和數學素養.下面從解三角形中“已知一角及一邊”的問題展開對相關問題的深入探究和系統認知.2010—2019年全國新課標高考試題中，“已知一角及其對邊”是高頻考點，與三角函數綜合考查并作為壓軸題的情況屢屢出現.我們先來看看這個模型.

模型1已知三角形的一角及其對邊

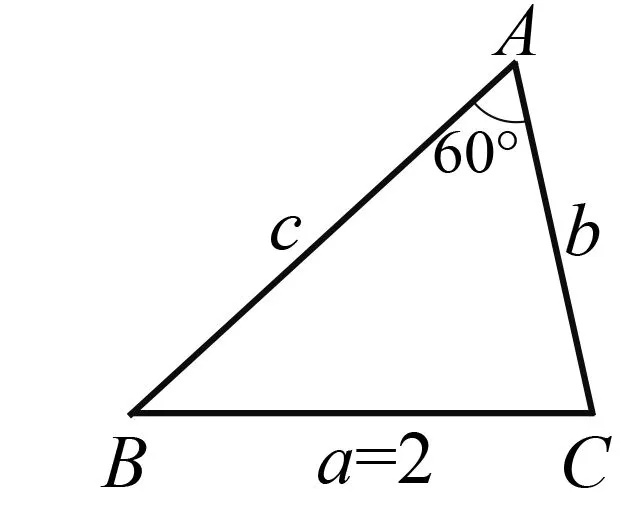
圖1

如圖1，在△ABC中，已知的三個內角為A，B，C，其對應的三邊為a,b,c，且A=60°，a=2(即已知三角形一角及其對邊)，則根據三角形的邊角關系就可得到以下三個隱含的解題條件：

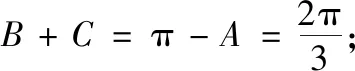
變形：4=(b+c)2-3bc.

以上三個隱含的解題條件深刻揭示了解三角形中“已知一角及其對邊”的本質：角的關系(內角和定理)、邊角的關系(正余弦定理)．掌握這個本質就可解決多種不同類型的問題，進而得到解決此類問題的系統方法.

例如，在上述條件下可求：(1)B+C；(2)△ABC外接圓的半徑；(3)sinB+ sinC的取值范圍(擴展到求t1sinB+t2sinC(t1t2≠0)的最值)；(4)b+c的取值范圍(擴展到求λb+μc(λμ≠0)的最值)；(5)△ABC周長的最大值(即求a+b+c的最大值)；(6)△ABC面積的最大值.

結合“已知三角形一角及其對邊”的三個隱含條件可知以上6個問題的解答為:

(1)(2)略.

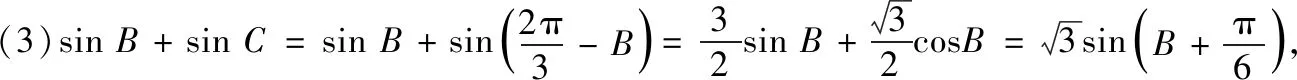
(5)△ABC的周長為a+b+c=2+b+c，轉化為問題(4)，可得周長的最大值為6．

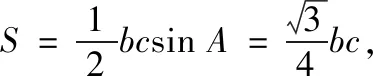
評析以上6個問題的求解過程深刻地展現了解三角問題中已知一角及其對邊的處理方法，揭示了三角形中邊角之間的相互轉化關系要靠正余弦定理來實現.該系統總結不僅強化了對解三角形中邊角關系的理解，而且求解過程中使用了三角恒等變換化簡三角函數式，利用三角函數圖象求解范圍的方法更是提升了學生對三角函數模塊的掌握和使用，鍛煉了學生的整體思維品質，提升了數學素養和能力.

下面我們再以模型1的問題(4)為出發點，結合高考試題的考查方向和特點，繼續深入探究解三角形中已知一角及其對邊模型的通性通法.

例在△ABC中，已知△ABC的三個內角為A，B，C，其對應的三邊為a，b，c，且A=60°，a=2，求b+c的取值范圍.

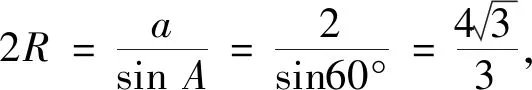
當然，如果采用一些技巧也可快速解決問題.我們來看看巧解并與通法進行對比.

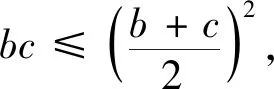
評析顯然，巧法利用不等式放縮快速解決了問題．乍一看非常完美實用，但如果稍加改變問題中的條件或結果，那么巧法將黯然失色.請看下面的變式.

變式1 在△ABC中，已知△ABC的三個內角為A，B，C，其對應的三邊為a，b，c，且A=60°，a=2，求2b+c的取值范圍.

變式2 在銳角三角形ABC中，已知△ABC的三個內角為A，B，C，其對應的三邊為a，b，c，且A=60°，a=2，求b+c的取值范圍.

更一般的有以下變式：

變式3 在△ABC中，已知△ABC的三個內角為A，B，C，其對應的三邊為a，b，c，且A=60°，a=2，求λb+μc(λμ≠0)的取值范圍.

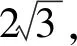
值得關注的是，2012年全國課標卷文理科17題、2010年全國課標卷理科16題、2014年全國課標卷Ⅰ理科16題、2013年全國課標卷理科18題、2016年全國課標卷Ⅰ理科18題、2017年全國課標卷Ⅰ理科18題都在考查解三角形中“已知一角及其對邊”的模型，而且均在模型1的問題(1)～(6)中進行考查.如果我們一線教師在教學中結合以上經驗，帶領學生深入探究思考，在解三角形模型1的基礎上提出問題：將模型1中的“已知一角及其對邊”更改為“已知一角及其一條鄰邊”，會出現什么樣的新問題呢？2019年高考全國新課標卷Ⅲ文理科的18題就給了我們答案！

模型2已知三角形的一角及其一條鄰邊

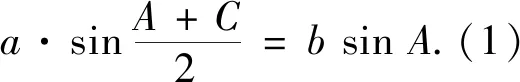
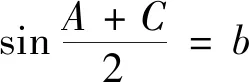
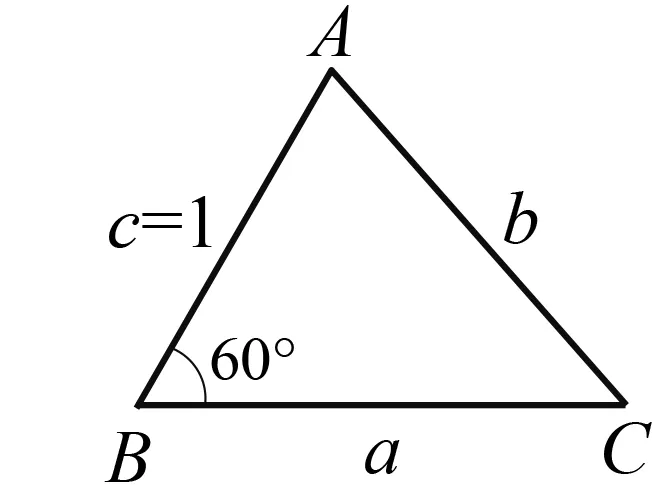
圖2

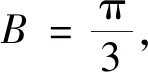
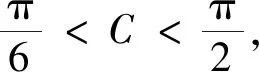
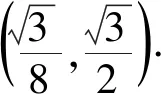
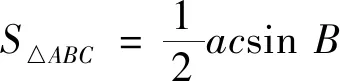
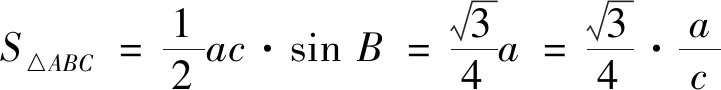
此題也可使用余弦定理求解，方法如下．

方法2看似簡潔實則計算龐大冗長，且在全用邊的不等式求解邊范圍的過程中容易出錯．故此法雖巧，但操作性不強，也不能深刻揭示出問題的本質， 故不宜用于解題教學，通法才是解決該問題的最佳方法.

通過模型1和模型2的通法討論，我們可以總結得到：在三角形中已知一邊和一角的系統求解策略是：將邊的表達式轉化為角的三角函數進行處理，這是通法. 而已知三角形的“一角兩邊”“兩角一邊” “三邊”等模型均可直接使用正余弦定理解三角形，且三角形是確定的，也就不存在求解范圍的問題了！這樣一來，解三角形中已知“一角一邊”的問題就得到了系統的認識，學生在教師的帶領下也就形成了解決三角形問題中已知邊角問題的整體解決方案，當然也就形成了解決一類問題的系統方法.可以想象，2020年高考數學全國新課標卷中解三角形問題仍將會是“寵兒”，希望以上的論述能夠給予備考的師生一些 幫助.