2019年中考中的傳統文化試題賞析*

王成良 羅 偉

(江蘇省常州市實驗初級中學 213000)(江蘇省徐州市第二十四中學 221000)

對于數學文化，顧沛教授認為：簡單地說，是指數學的思想、精神、方法、觀點以及它們的形成和發展；廣泛些說，除了上述內涵以外，還包含數學家、數學史、數學美、數學教育、數學發展中的人文成分，數學與社會的聯系，數學與各種文化的關系等．喻平教授認為：每一個中考試題都蘊含一定的數學思想方法，都具有數學文化．而傳統文化試題，相對來說文化成分的呈現方式是明顯的，在各地中考試題中頻繁出現．筆者選取2019年部分中考試題進行研究，包含中國傳統文化與數學的融合、中國古代數學名著中的問題、中國古代著名的數學問題、外國傳統文化試題四方面，現選取部分經典題目進行賞析．

1 中國傳統文化與數學的融合

在中國傳統文化中，有許多具有代表性的東西，為人們的生活帶來了便利，促進了人們健康文明的生活.這些與數學也有一定的關系，在中考中經常能見到它們的身影．如甘肅隴南的象棋與坐標，甘肅天水的太極與概率，湖北武漢的“漏壺”與函數，四川達州的剪紙與軸對稱圖形，江蘇蘇州的七巧板與正方形邊長，山東濟寧的“三孔”、5G網絡與分式方程，都顯出了傳統文化與數學的融合．

例1(甘肅隴南)中國象棋是中華名族的文化瑰寶，因趣味性強而深受大眾喜愛．如圖1，若在象棋棋盤上建立平面直角坐標系，使“帥”位于點(0,-2)，“馬”位于點(4,-2)，則“兵”位于點．

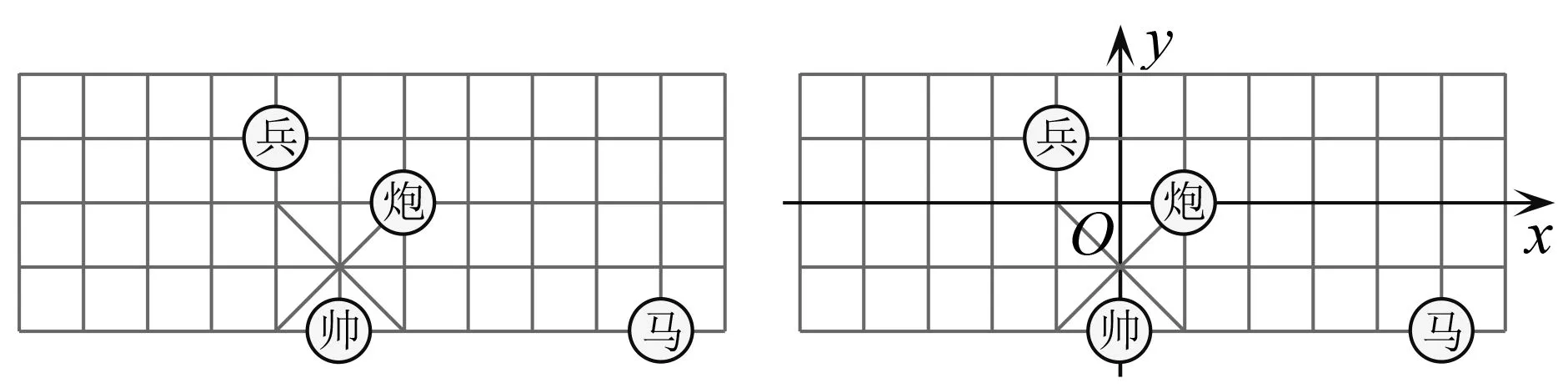
圖1 圖2

思路 根據“帥”“馬”的坐標先確定原點的位置．

解根據題意可得原點位置，建立直角坐標系，如圖2所示，則“兵”位于點(1,-1)．

賞析本題考查了直角坐標系、點的坐標，解題的關鍵是確定坐標系中原點的位置．象棋是中國的傳統，不僅是一種老少皆宜的娛樂活動，還蘊含著豐富的哲理以及許多數學知識．把棋子看作點，不同的點也就有了不同的坐標．本題還可再增加一個問題：“若下棋時出‘馬’，則‘馬’移動后的坐標為．”這樣使傳統文化與數學進一步融合，顯示出數學的趣味性和應用廣泛性．

2 中國古代數學名著中的問題

中國古代有許多數學名著，記錄了數學文化的發展歷程，為中國數學文化的傳播做出了重要的貢獻．近年來，一些中考題便從這些名著中選取，其中考查頻率最多的是《九章算術》，另外還有《孫子算經》《周髀算經》《算學啟蒙》《增刪算法統宗》《御制數理精蘊》《洛書》等；從內容上，主要考查一元一次方程、二元一次方程組的列法、解法，有的要求列出方程或方程組，有的則需要求出結果．另外也有試題涉及函數、勾股定理等知識．

例2(山東泰安)《九章算術》是我國古代數學的經典著作，書中有一個問題：“今有黃金九枚，白銀一十一枚，稱之重適等，交易其一，金輕十三兩，問金、銀一枚各重幾何？”意思是：甲袋中裝有黃金9枚(每枚黃金重量相同)，乙袋中裝有白銀11枚(每枚白銀重量相同)，稱重兩袋相等，兩袋互相交換1枚后，甲袋比乙袋輕了13兩(袋子重量忽略不計)，問黃金、白銀每枚各重多少兩？設每枚黃金重x兩，每枚白銀重y兩，根據題意可列方程組為．

思路 根據題意先找出題目中的兩個等量關系： ①9枚黃金的重量=11枚白銀的重量；②(10枚白銀的重量+1枚黃金的重量)-(1枚白銀的重量+8枚黃金的重量)=13兩．

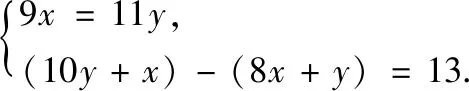
賞析此題主要考查由實際問題抽象出二元一次方程組，關鍵是正確理解題意，找出題目中的等量關系．

《九章算術》成書于公元1世紀，是中國乃至東方第一部自成體系的數學專著，總結了戰國、秦、漢時期的數學成就，創立了機械化算法體系．其內容十分豐富，全書采用問題集的形式，收有246個與生產、生活實踐有聯系的應用問題，這些問題依照性質和解法分別隸屬于方田、粟米、衰分、少廣、商功、均輸、盈不足、方程及勾股共九章．本題為盈不足問題．《九章算術》中的算法比歐洲同類算法早1 500多年，對世界數學發展產生了重要的影響．《九章算術》的問題在中考中大都是出示文言文之后又給出了現代文翻譯，主要是考慮到初中學生的閱讀能力．

例3(浙江金華)元朝朱世杰的《算學啟蒙》一書記載：“今有良馬日行二百四十里，駑馬日行一百五十里．駑馬先行一十二日，問良馬幾何日追及之．”圖3是兩匹馬行走路程S關于行走時間t的函數圖象，則兩圖象交點P的坐標是．

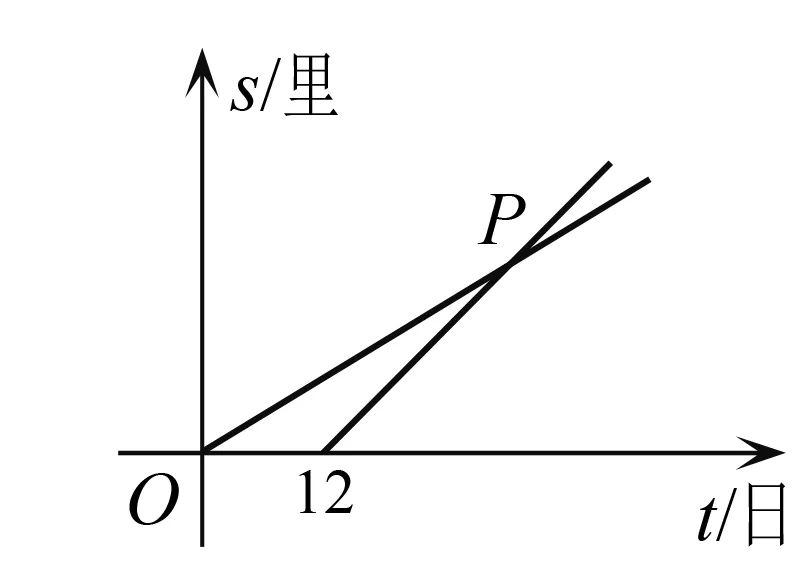
圖3

思路 從問題看，是追及問題，可以通過設未知數列一元一次方程求出時間t，再結合圖3中一次函數與正比例函數的圖象即可求出點P的坐標．

解根據題意得150t=240(t-12)，解得t=32，150t=150×32=4 800，故點P的坐標為(32, 4 800)．

賞析本試題出示的文言文相對簡單，絕大多數學生能看懂，所以沒有給出現代文翻譯．從圖象看，點是一次函數與正比例函數的圖象的交點，從問題敘述來看，則是追及問題，所以列一元一次方程求解比求出兩個函數再求交點坐標更簡單易懂．

《算學啟蒙》是元朝朱世杰所著，全書共三卷，20門，總計259個問題和相應的解答．包括從乘除法運算及其捷算法到開方、天元術、方程等數學各方面，由淺人深，形成了一個較完整的體系． 其中正負數乘法法則不僅是在中國數學著作中，也是在世界上首次出現．該著作曾流傳海外，影響了朝鮮、日本數學的發展．本題則主要為方程問題．

3 中國古代著名的數學問題

在中考中，有時涉及中國古代著名的數學問題，如浙江寧波的勾股定理應用、浙江紹興的幻方計算、臺灣的勾股容圓計算等.在這些計算中可以發現古代數學的智慧．

例4(浙江寧波)勾股定理是人類最偉大的科學發現之一，在我國古算書《周髀算經》中早有記載．如圖4，以直角三角形的各邊為邊分別向外作正方形，再把較小的兩張正方形紙片按圖5的方式放置在最大正方形內．若知道圖中陰影部分的面積，則一定能求出( )．

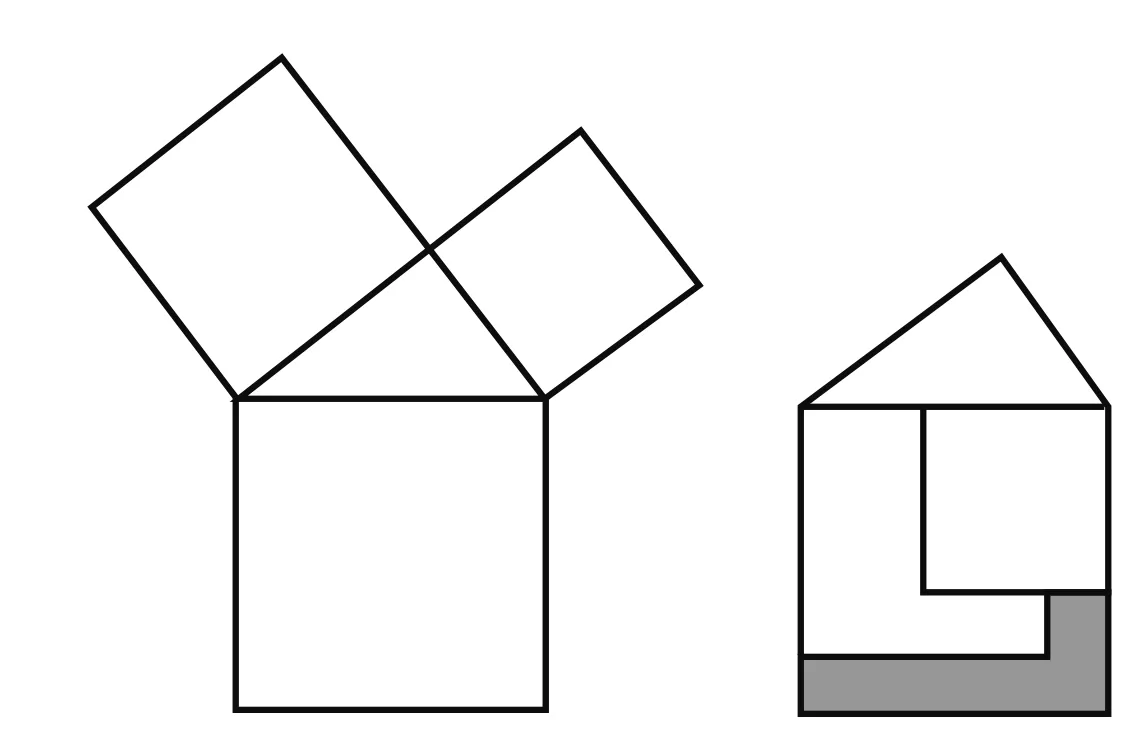
圖4 圖5

A．直角三角形的面積

B．最大正方形的面積

C．較小兩個正方形重疊部分的面積

D．最大正方形與直角三角形的面積和

思路 先把直角三角形的三邊分別用a,b,c表示出來，再把陰影部分的面積表示出來之后，與四個選項對比．

解設直角三角形較短直角邊為a，較長直角邊為b，斜邊長為c．由勾股定理得a2+b2=c2，陰影部分的面積為c2-b2-a(c-b)=a2-ac+ab=a(a+b-c)，較小兩個正方形重疊部分的長為a，寬為a-(c-b)，面積為a[a-(c-b)]=a(a+b-c)，恰好等于陰影的面積，故選C．

賞析本題考查勾股定理的內容及折疊等知識，需要較強的空間想象能力，具體做題時學生可以動手折疊，培養幾何直觀能力及思維能力．

《周髀算經》原名《周髀》，算經的十書之一，是中國最古老的天文學和數學著作，約成書于公元前1世紀，主要闡明當時的蓋天說和四分歷法．唐初規定它為國子監明算科的教材之一．勾股定理是人類寶貴的財富，被稱為千古第一定理，是數形結合的典范，中國古代《周髀算經》最早有相關的記載，在國外則相傳為古希臘畢達哥拉斯發現．

4 外國傳統文化試題

也有許多有關外國傳統文化的試題出現在中考中，如浙江衢州的“三等分角”、浙江溫州的《幾何原本》相關的內容、江蘇揚州的哥德巴赫猜想、江蘇徐州的斐波那契數列，這些內容值得我們去學習．

圖6

例5(浙江衢州)“三等分角”大約是在公元前5世紀由古希臘人提出來的．借助如圖6所示的“三等分角儀”能三等分任一角．這個三等分角儀由兩根有槽的棒OA,OB組成，兩根棒在點O相連并可繞O轉動，點C固定，OC=CD=DE，點D,E可在槽中滑動，若∠BDE=75°，則∠CDE的度數是( )．

A．60° B．65° C．75° D．80°

思路 求∠CDE的度數可根據“三等分角儀”中給出的三條相等的線段，轉化為兩對相等的角，再結合三角形內角和等知識求解．

解因為OC=CD=DE，所以∠O=∠ODC，∠DCE=∠DEC．設∠O=∠ODC=x°，則∠DCE=∠DEC=2x°，所以∠CDE=180°-∠DCE-∠DEC=180°-4x°．因為∠ODC+∠CDE+∠BDE=180°，所以x+(180-4x)+75=180，解得x=25，所以∠CDE=180°-4x°=80°．故答案為D．

賞析三等分角是古希臘人提出來的一個古老的數學問題，只借助直尺和圓規把一個角三等分，與化圓為方、立方倍積問題并列稱為古代數學的三大難題，包括阿基米德在內的許多數學家都沒有做出來，如今證實了這個問題無解．本題的“三等分角”加上了三條線段相等的條件，用到了度量，故不是真正意義上的三等分角，但這種方法卻給實際生活帶來了方便.比如圖6中，先調整儀器，使∠BDE與所要測量的角重合，然后再把點O移到與點D重合，沿OA就可以畫出它的一條三等分線，題目要是再說清楚使用方法就更好了，這體現了數學的應用意識與創新意識．

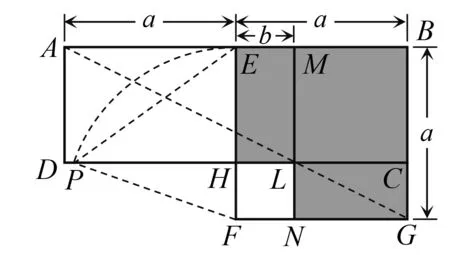
圖7

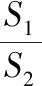
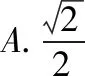
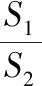
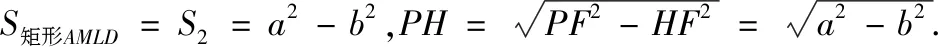
賞析本題通過圖形展示了平方差公式的證明方法，但接下來的問題比較難，是選擇題的壓軸題，考查數形結合的思想，運用了勾股定理、相似、換元等知識和方法，需要較強的思維能力．

《幾何原本》是古希臘數學家歐幾里得所著的一部數學著作，成書于公元前300年左右，又稱《原本》，它是歐洲數學的基礎，總結了平面幾何五大公設，創立了邏輯演繹體系，被廣泛地認為是歷史上最成功的教科書，以嚴謹的幾何論證聞名，決定了整個西方數學和科學的發展史．

在以后的教學中，教師可以多精選蘊含傳統文化的題目讓學生去閱讀、欣賞和解答．首先，在課本中有不少它們的身影，讓學生仔細品味傳統文化的精髓所在．其次，在一些中考題中引導學生去發現這類問題所需要的知識、思想、方法，不斷進行總結．另外，教師可以把《九章算術》《孫子算經》《幾何原本》等圖書放到教室供學生課余時閱讀并寫些心得體會，讓學生體會傳統文化之美，領略中外數學精神，進而提升自己的數學文化素養．