自定義工具，讓GeoGebra如虎添翼*

羅建宇

(江蘇省張家港市沙洲中學(xué) 215600)

在“互聯(lián)網(wǎng)+”時(shí)代，有效應(yīng)用技術(shù)以解決教與學(xué)的實(shí)際問題，推動(dòng)學(xué)生對(duì)數(shù)學(xué)本質(zhì)的認(rèn)識(shí)和數(shù)學(xué)思維的提升，已成為當(dāng)下數(shù)學(xué)教育工作者面臨的新課題．GeoGebra(簡(jiǎn)稱GGB)作為一款“專為教與學(xué)的動(dòng)態(tài)數(shù)學(xué)軟件”，能實(shí)現(xiàn)幾何作圖、代數(shù)運(yùn)算和數(shù)據(jù)處理等的跨平臺(tái)聯(lián)動(dòng)，能深入學(xué)科內(nèi)部而幫助學(xué)習(xí)者洞悉數(shù)學(xué)本質(zhì)，能構(gòu)建“抽象的數(shù)”與“可見的形”間的聯(lián)系通道而提升思維層次，更能突破數(shù)學(xué)“難以意會(huì)、無法言傳”的障礙而轉(zhuǎn)變學(xué)習(xí)方式.于是,讓GGB走進(jìn)課堂，實(shí)現(xiàn)GGB與數(shù)學(xué)教與學(xué)的深度融合，已成為諸多一線教師的共同選擇，“懂得GGB，她就給你獨(dú)到眼光，讓你洞悉數(shù)學(xué)世界”[1]．

GGB中有著多樣的工具和豐富的指令，與之相對(duì)應(yīng)的是，構(gòu)造數(shù)學(xué)對(duì)象時(shí)有工具構(gòu)造和指令輸入兩種基本方式．前者是所有動(dòng)態(tài)幾何軟件的通用方法，具有面向?qū)ο蟮膬?yōu)勢(shì)，操作方式直觀易懂；后者恰是GGB的一個(gè)顯著特色，只要在指令輸入框中輸入相應(yīng)指令，便可實(shí)現(xiàn)數(shù)學(xué)對(duì)象的構(gòu)造．在教學(xué)實(shí)踐中，我們發(fā)現(xiàn)GGB中更有創(chuàng)建自定義工具的功能，當(dāng)我們將需要重復(fù)構(gòu)造的對(duì)象自動(dòng)“記憶”成工具后，便可以如同復(fù)制粘貼一樣反復(fù)使用，可以說自定義工具讓GGB如虎添翼，帶來的是更加靈動(dòng)的數(shù)學(xué)和便捷的學(xué)習(xí)．本文以GeoGebra Classic 5.0.553.0-d版本(中文界面)為例，談?wù)勅绾蝿?chuàng)建自定義工具以及如何應(yīng)用自定義工具推動(dòng)深度學(xué)習(xí)，進(jìn)而發(fā)展學(xué)生數(shù)學(xué)學(xué)力．

1 自定義工具的創(chuàng)建舉例

1.1 阿波羅尼斯圓的構(gòu)造

到兩定點(diǎn)A,B的距離之比為定值t(t>0且t≠1)的點(diǎn)P的軌跡為圓.這個(gè)結(jié)論是阿波羅尼斯(Apollonius,約公元前260-前190)發(fā)現(xiàn)的，所以稱為阿波羅尼斯圓(簡(jiǎn)稱阿氏圓)．

如圖1，阿氏圓以MN為直徑，因此構(gòu)造的關(guān)鍵是找到點(diǎn)M,N，其中點(diǎn)M在線段AB上(稱為A,B的內(nèi)分點(diǎn))，點(diǎn)N在線段AB的延長(zhǎng)線上(稱為A,B的外分點(diǎn))．

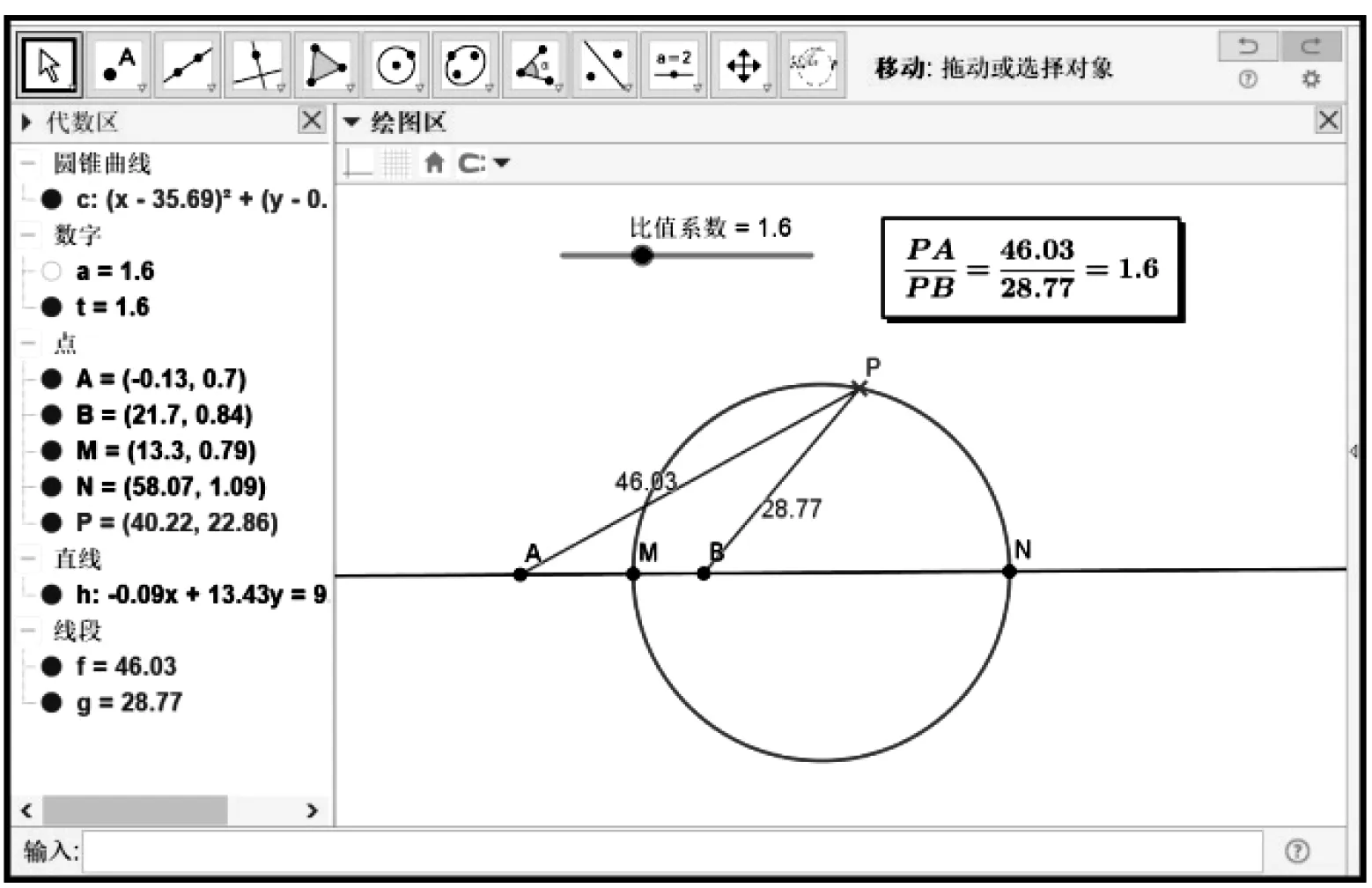
圖1

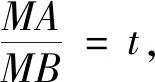
(1)新建窗口，構(gòu)造滑動(dòng)條t(范圍0～5)，構(gòu)造任意兩點(diǎn)A，B；輸入指令“位似(B,t/(t+1),A)”“位似(B,t/(t-1),A)”，得到阿氏圓的直徑端點(diǎn)M,N．

說明“位似”指令的語法結(jié)構(gòu)為“位似(<幾何對(duì)象>,<位似比>,<位似中心> )”，這樣以點(diǎn)A為中心、以t/(t+1)為位似比，將點(diǎn)B縮放得到點(diǎn)B，相較幾何畫板而言，GGB的構(gòu)造要簡(jiǎn)捷許多[2]．

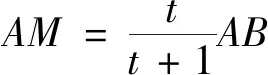
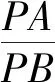
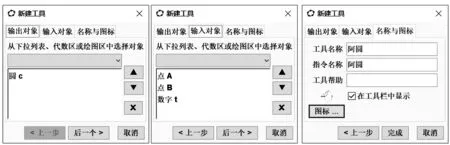
圖2

說明相較幾何畫板而言，GGB中創(chuàng)建自定義工具更加智能，當(dāng)我們選定“輸出對(duì)象”時(shí)，軟件會(huì)自動(dòng)提示構(gòu)造對(duì)象的父對(duì)象(即先決條件)為“輸入對(duì)象”(通常默認(rèn)即可，也可在下拉菜單中重新選擇或更改順序)．

1.2 橢圓光學(xué)性質(zhì)的擬合

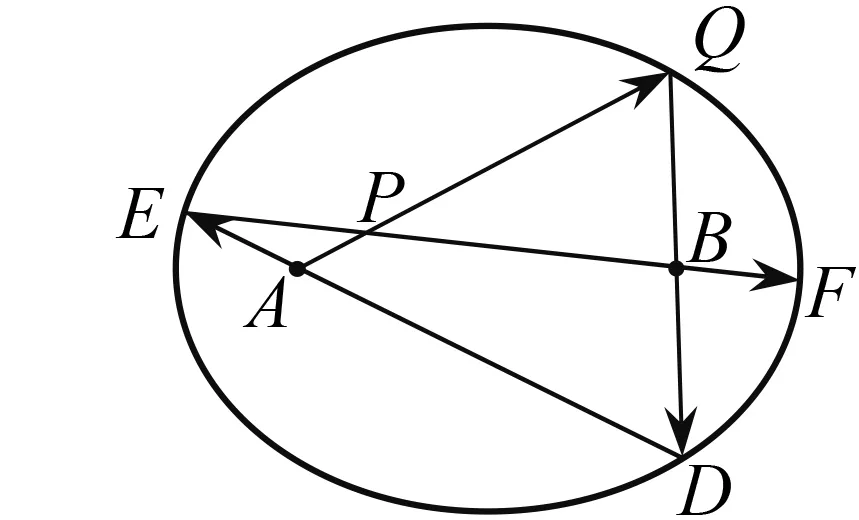
圖3

如圖3，光線PQ經(jīng)過橢圓一個(gè)焦點(diǎn)A，經(jīng)橢圓內(nèi)壁位置Q反射后得到的反射光線必經(jīng)過另一焦點(diǎn)B，這就是橢圓的光學(xué)性質(zhì)．橢圓的光學(xué)性質(zhì)在生產(chǎn)與科技方面有著廣泛應(yīng)用，如電影放映機(jī)的聚光燈泡以及光能的換位聚焦等就是利用橢圓的這一性質(zhì)．

(4)新建窗口，構(gòu)造任意三點(diǎn)A,B,C，輸入指令“橢圓(A,B,C)”得到橢圓c；構(gòu)造橢圓c內(nèi)一點(diǎn)P和橢圓c上一點(diǎn)Q．

(5)輸入指令“切線(Q,c)”，得到橢圓c在點(diǎn)Q處的切線f；輸入指令“反射(P,f)”，得到P關(guān)于f的反射點(diǎn)P′；輸入指令“射線(P′,Q)”，得到射線g；輸入指令“交點(diǎn)(c,g,2)”，得到射線g與橢圓c的第2個(gè)交點(diǎn)R．

說明(5)中的四步操作可以用一句指令“交點(diǎn)(c,射線(對(duì)稱(P,切線(Q,c)),Q),2)”來替代，在減少中間對(duì)象的同時(shí)提高構(gòu)造效率，體現(xiàn)指令輸入法快捷靈動(dòng)的特性．

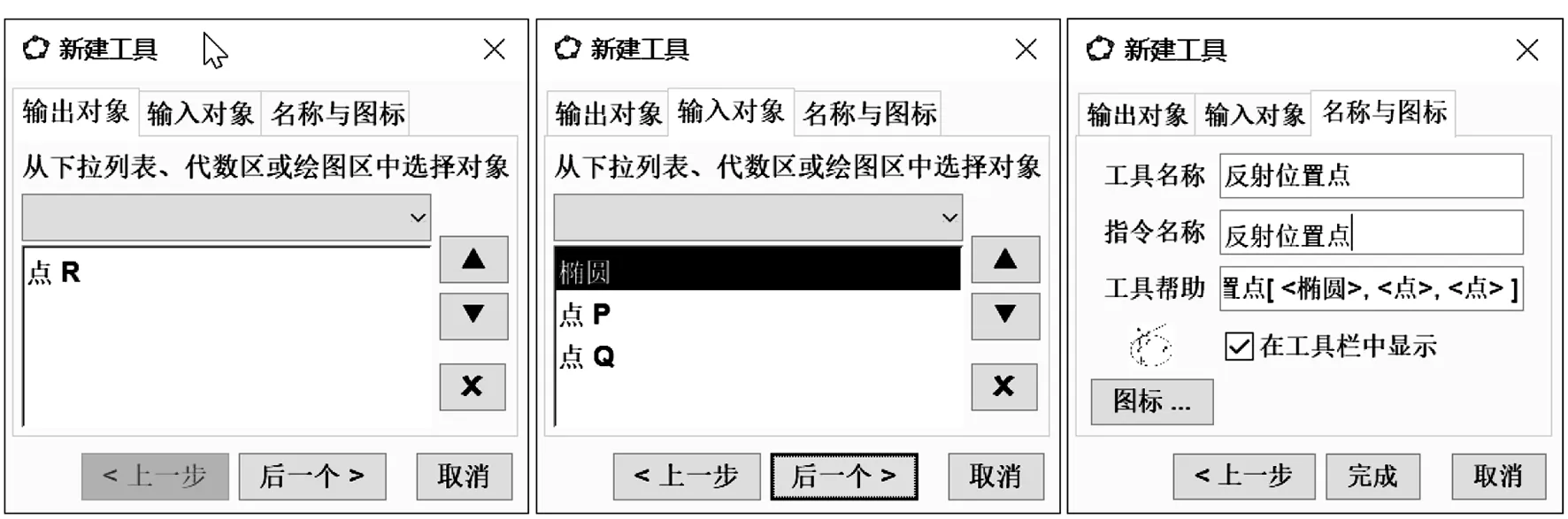
圖4

說明在自定義工具時(shí)需要特別注意“輸入對(duì)象”的順序，“輸入對(duì)象”的順序直接決定了自定義工具的語法法則.如本例語句“反射位置點(diǎn)(c,P,Q)”中，P為起始點(diǎn)，Q為反射點(diǎn)，得到的點(diǎn)D為反射位置點(diǎn)．

2 自定義工具的應(yīng)用

從上述兩個(gè)案例可以發(fā)現(xiàn)，GGB中創(chuàng)建自定義工具還是比較方便的，我們可以將一系列操作整體打包定義為一個(gè)工具(指令)，一旦定義成功，便可以在菜單工具欄中調(diào)用，也可作為指令在指令區(qū)輸入.(3)和(6)中涉及的只是自定義工具的簡(jiǎn)單應(yīng)用，如果加上“迭代”“序列”指令， 帶給我們的將不僅是令人震驚的視覺沖擊，更有豁然開朗后的數(shù)學(xué)理解．

2.1 構(gòu)建有趣的數(shù)學(xué)情境

橢圓的光學(xué)性質(zhì)對(duì)學(xué)生而言不難理解，然而當(dāng)光線無數(shù)次反射后呢？結(jié)果卻有著異樣的精彩：當(dāng)入射光線經(jīng)過橢圓的一個(gè)焦點(diǎn)時(shí)，反射光線經(jīng)過另一焦點(diǎn)的同時(shí)向長(zhǎng)軸方向“聚合”(圖5(1)).而當(dāng)入射光線不過焦點(diǎn)時(shí)，反射光線構(gòu)成的輪廓(或者說包絡(luò))為圓錐曲線，其中點(diǎn)P位于A,B之外(在橢圓內(nèi))時(shí)，輪廓為橢圓(圖5(2))；點(diǎn)P位于A,B之間時(shí)，輪廓為雙曲線(圖5(3))．而“發(fā)現(xiàn)”這樣的結(jié)論只需要增加一行指令：

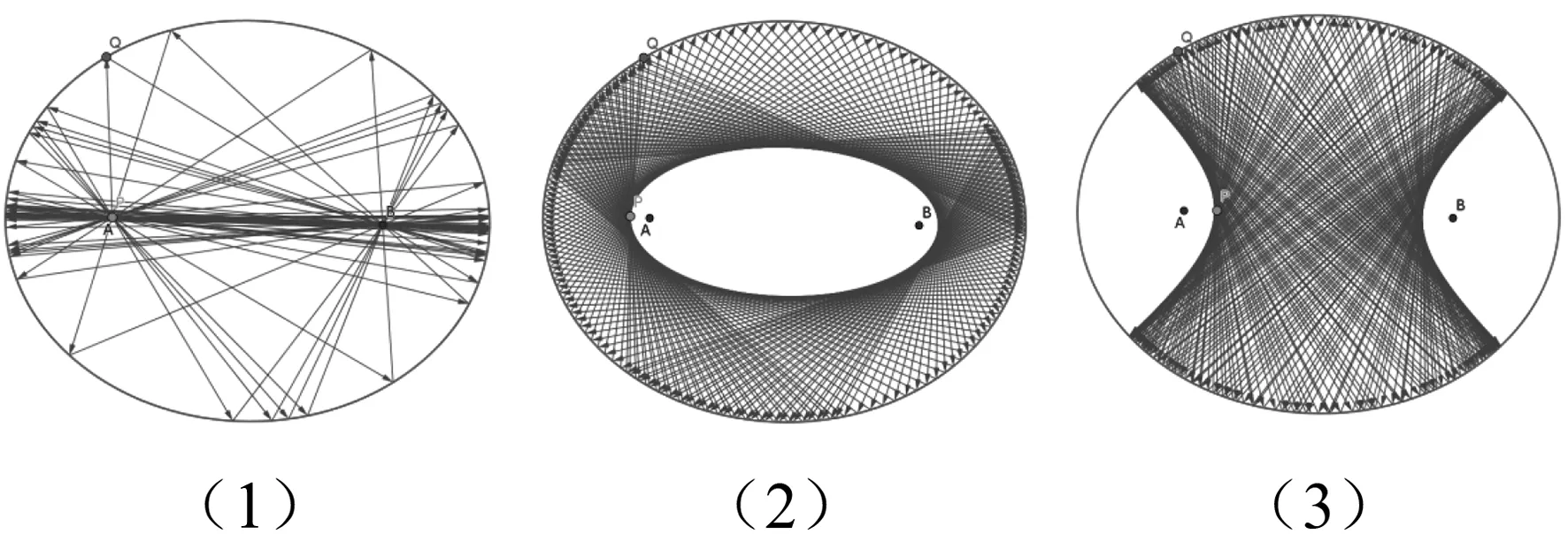
圖5

(7)構(gòu)造整數(shù)滑動(dòng)條n(范圍1～100)，輸入指令“迭代列表(反射位置點(diǎn)(c,P,Q),P,Q,{P,Q},n)”，得到列表l1；輸入指令“序列(向量(元素(列表1,i), 元素(列表1,i+1)),i,1,n,1)”，得到列表l2．

數(shù)學(xué)的學(xué)習(xí)離不開情境的作用，數(shù)學(xué)概念的理解、數(shù)學(xué)命題的掌握、數(shù)學(xué)技巧的形成、數(shù)學(xué)思想的應(yīng)用、數(shù)學(xué)問題的解決都要基于數(shù)學(xué)情境的創(chuàng)設(shè)、運(yùn)行、反思來完成．應(yīng)用自定義工具可以創(chuàng)設(shè)有趣的數(shù)學(xué)情境，從簡(jiǎn)單到復(fù)雜、由已知探未知，復(fù)雜多變的圖形背后蘊(yùn)涵著深刻的數(shù)學(xué)規(guī)律，正如“以境啟知，由知怡情”．?dāng)?shù)學(xué)情境是產(chǎn)生數(shù)學(xué)學(xué)習(xí)的條件，只有學(xué)生積極主動(dòng)地參與進(jìn)來，課堂氛圍才能活躍、教學(xué)效果才能凸顯．

2.2 實(shí)現(xiàn)有勁的深度學(xué)習(xí)

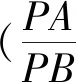
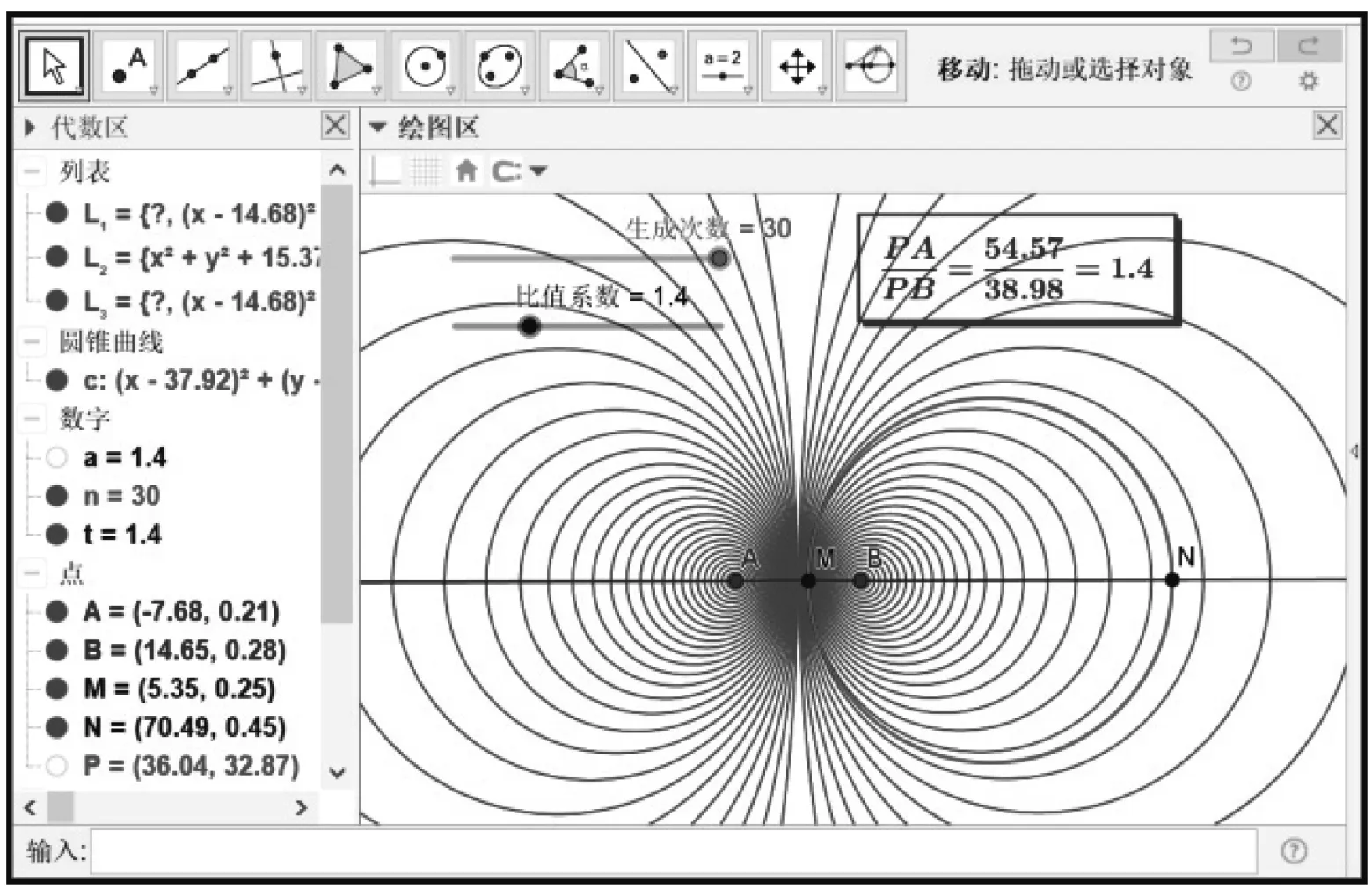
圖6

2.3 推動(dòng)有用的應(yīng)用探索

我們知道，玫瑰線的極坐標(biāo)方程為ρ=asinkθ，如果說輸入“曲線((a+sin(kθ);θ),θ,0,2π)”可以揭開玫瑰線神秘面紗的話,那么將玫瑰線定義為工具1，輸入“序列(工具1(t,k),t,0,5,0.2)”，則可以從整體上探究玫瑰線背后的數(shù)學(xué)故事．事實(shí)上，系數(shù)a決定玫瑰線的線徑，參數(shù)k則決定花瓣數(shù)，當(dāng)k是奇數(shù)時(shí)玫瑰線有k個(gè)花瓣(圖7)，當(dāng)k是偶數(shù)時(shí)玫瑰線則有2k個(gè)花瓣(圖8)．以此為基礎(chǔ)，可以將玫瑰線應(yīng)用于生活中，設(shè)計(jì)成窗簾、地毯圖案來裝扮我們的生活，正如數(shù)學(xué)源于生活又應(yīng)用于生活．

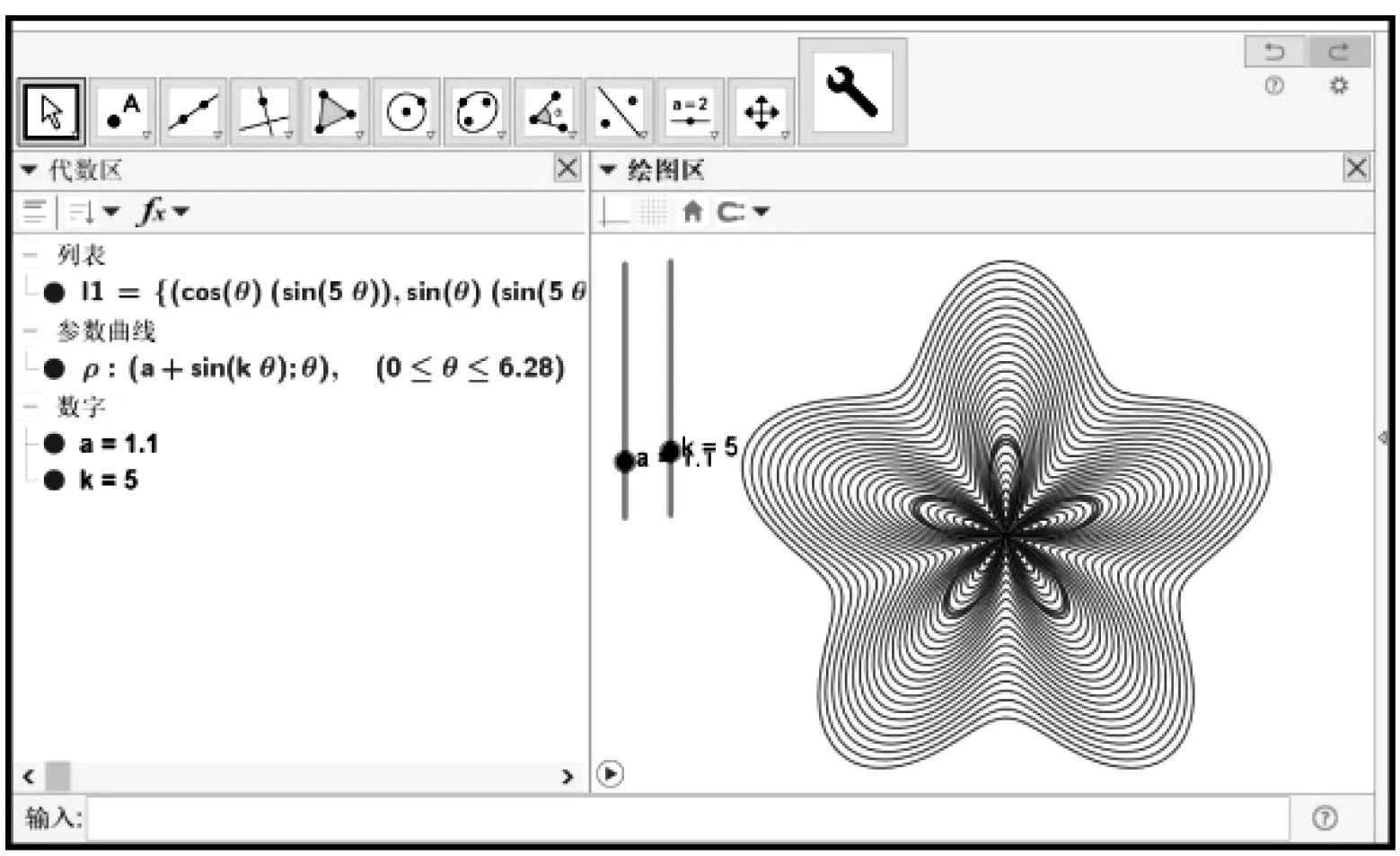
圖7

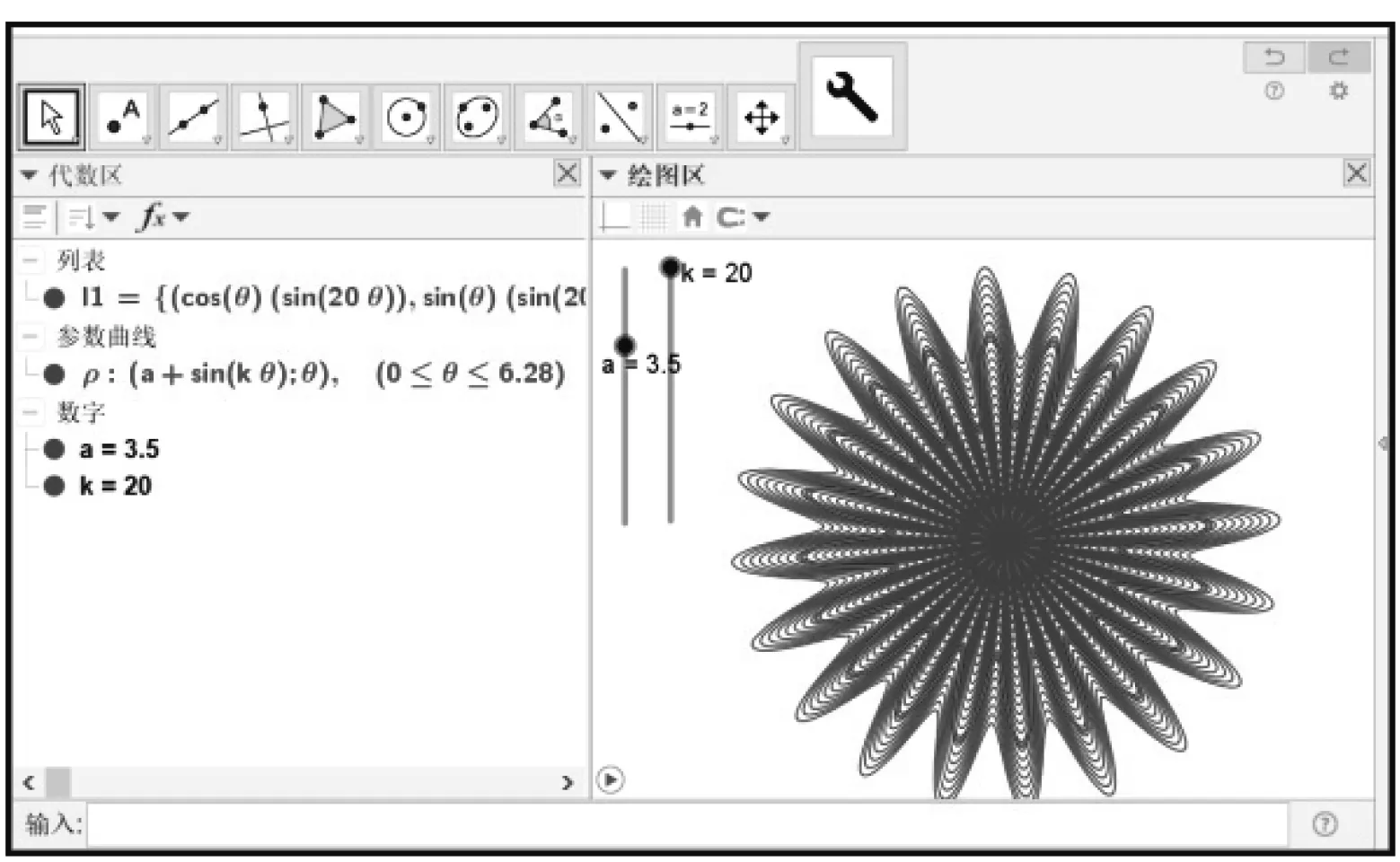
圖8

GGB走進(jìn)課堂，構(gòu)建了交互式、多樣化的學(xué)習(xí)環(huán)境，也讓數(shù)學(xué)的推理演繹過程可視化；而創(chuàng)設(shè)、應(yīng)用自定義工具，呈現(xiàn)不一樣的數(shù)學(xué)的同時(shí)，也讓學(xué)生對(duì)數(shù)學(xué)有用、有趣有了直接的感知，從而保證學(xué)生可以“看他們以往只能‘想象’的數(shù)學(xué)，‘做’他們以往不能做的數(shù)學(xué)”．當(dāng)然，發(fā)揮教育技術(shù)在數(shù)學(xué)教學(xué)中的優(yōu)勢(shì)，需要更好地理解數(shù)學(xué)教學(xué)中的技術(shù)，不斷地挖掘和開發(fā)課程資源，用“火熱的思考”融化“冰冷的美麗”，唯其如此才能推動(dòng)學(xué)生的數(shù)學(xué)思維往更高層次發(fā)展．