培養(yǎng)平面向量語(yǔ)言能力的目標(biāo)與手段

沈 健

(江蘇省太倉(cāng)高級(jí)中學(xué) 215411)

數(shù)學(xué)語(yǔ)言能力的培養(yǎng)是數(shù)學(xué)教育的重要任務(wù)之一，它是數(shù)學(xué)素養(yǎng)的關(guān)鍵因素.平面向量(以下不特別說(shuō)明，向量均指平面向量)有著豐富的圖形內(nèi)涵和縝密的運(yùn)算特征，因此它是除解析法之外，聯(lián)系代數(shù)和幾何最有效的工具，它能把抽象問(wèn)題直觀化，充分體現(xiàn)了數(shù)形結(jié)合思想.向量的數(shù)學(xué)價(jià)值及向量學(xué)習(xí)價(jià)值的體現(xiàn)，必須以向量語(yǔ)言為載體，以向量語(yǔ)言能力的培養(yǎng)為目標(biāo).

1 向量語(yǔ)言和向量語(yǔ)言能力

1.1 向量語(yǔ)言的內(nèi)涵

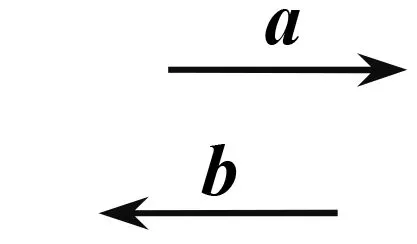
圖1

向量語(yǔ)言是描述向量的概念、關(guān)系、運(yùn)算和規(guī)律，且具有特定形式的一種數(shù)學(xué)語(yǔ)言.這里的特定形式主要包括文字形式和符號(hào)形式.如在描述兩向量a,b的共線關(guān)系時(shí)，可以有以下不同的形式：①文字形式：向量a,b共線； ②符號(hào)形式：a∥b或者a=λb(b≠0,λ∈R且唯一)；③圖形形式：如圖1.

從語(yǔ)言的內(nèi)涵來(lái)看，向量語(yǔ)言有表示抽象概念的，如0表示零向量；有表示關(guān)系的，如a=-b表示兩向量互為反向量；有表示向量運(yùn)算的，如a·b表示兩向量作數(shù)量積運(yùn)算；有表示規(guī)律的，如λa=aλ表示實(shí)數(shù)與向量的積滿足交換律.以上諸例體現(xiàn)出向量語(yǔ)言形式的多樣性和內(nèi)涵的豐富性，它是描述向量?jī)?nèi)容的工具，是向量思想方法建立的載體.

1.2 向量語(yǔ)言能力

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版)》(以下簡(jiǎn)稱《標(biāo)準(zhǔn)》)[1]在課程目標(biāo)中明確闡述了在學(xué)習(xí)數(shù)學(xué)和應(yīng)用數(shù)學(xué)的過(guò)程中，學(xué)生能發(fā)展數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、直觀想象、數(shù)學(xué)運(yùn)算、數(shù)據(jù)分析等數(shù)學(xué)學(xué)科核心素養(yǎng)，提高從數(shù)學(xué)角度發(fā)現(xiàn)和提出問(wèn)題、分析和解決問(wèn)題的能力；同時(shí)在主題三“幾何與代數(shù)”說(shuō)明中提出，能用向量語(yǔ)言和方法表述和解決數(shù)學(xué)和物理中的一些問(wèn)題，發(fā)展運(yùn)算能力和解決實(shí)際問(wèn)題的能力.

《標(biāo)準(zhǔn)》對(duì)向量語(yǔ)言能力的要求是非常明確的，而對(duì)于利用向量推理論證、運(yùn)算求解、關(guān)系處理、用向量的方法處理實(shí)際問(wèn)題等一系列的與向量有關(guān)的能力，必須建立在一定水平的向量語(yǔ)言能力之上，它是形成和提高其他能力的基礎(chǔ)和必備條件.向量的語(yǔ)言能力應(yīng)該包括以下不同的幾個(gè)方面：①對(duì)向量抽象符號(hào)意義理解的能力；②對(duì)向量語(yǔ)言內(nèi)涵挖掘的能力；③向量語(yǔ)言的各種形式之間的轉(zhuǎn)化能力；④把向量語(yǔ)言轉(zhuǎn)化其他數(shù)學(xué)語(yǔ)言的能力；⑤利用向量語(yǔ)言進(jìn)行推理論證、運(yùn)算求解的能力；⑥在向量思想方法的指導(dǎo)下利用向量語(yǔ)言解決問(wèn)題的能力.向量語(yǔ)言能力的形成，有助于對(duì)向量知識(shí)的理解和深化，有助于學(xué)生思維能力的培養(yǎng)和提高，有利于培養(yǎng)學(xué)生的數(shù)學(xué)基本素質(zhì).

2 向量語(yǔ)言能力的培養(yǎng)目標(biāo)

針對(duì)向量語(yǔ)言能力的不同側(cè)面，在學(xué)生原有知識(shí)結(jié)構(gòu)和認(rèn)知規(guī)律的基礎(chǔ)之上，向量語(yǔ)言教學(xué)應(yīng)該注重以下幾個(gè)方面：①了解向量豐富的實(shí)際背景，經(jīng)歷從具體問(wèn)題抽象出向量概念和符號(hào)的過(guò)程，理解向量符號(hào)的內(nèi)涵，建立符號(hào)感；②在實(shí)際問(wèn)題背景中，理解幾種向量運(yùn)算的運(yùn)算法則、運(yùn)算律及其幾何意義，并能用向量語(yǔ)言的坐標(biāo)形式進(jìn)行各種向量運(yùn)算；③能嫻熟地在向量語(yǔ)言的各種形式間相互轉(zhuǎn)換；④能夠?qū)⑾蛄空Z(yǔ)言轉(zhuǎn)化為圖形、坐標(biāo)、方程等其他可操作的數(shù)學(xué)語(yǔ)言，形成語(yǔ)言轉(zhuǎn)化意識(shí)；⑤通過(guò)向量語(yǔ)言的學(xué)習(xí)和使用，體會(huì)向量語(yǔ)言的簡(jiǎn)潔性、準(zhǔn)確性、多樣性及深刻的內(nèi)涵性和廣泛的應(yīng)用性，從而形成用向量的思想方法思考和解決問(wèn)題.

3 向量語(yǔ)言能力培養(yǎng)的手段

3.1 理解概念內(nèi)涵，諳熟符號(hào)表達(dá)

深刻理解概念、法則、規(guī)律的內(nèi)涵，諳熟它們的符號(hào)表達(dá)形式，是向量語(yǔ)言能力形成和提高的基礎(chǔ)及保證.符號(hào)以及符號(hào)構(gòu)成的表達(dá)式是向量語(yǔ)言的主要表述形式，幾乎所有的向量?jī)?nèi)容都有其固定的符號(hào)描述.所以對(duì)相關(guān)符號(hào)的意義的理解是使用向量語(yǔ)言、形成向量語(yǔ)言能力的基礎(chǔ).在教學(xué)過(guò)程中，應(yīng)注意以下兩個(gè)問(wèn)題.

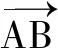
②注意形式相近易混淆的向量語(yǔ)言.向量語(yǔ)言中有很多形式相近的內(nèi)容，在學(xué)習(xí)過(guò)程中必須要在透徹理解有關(guān)內(nèi)容的基礎(chǔ)上加以明確區(qū)分，若不然肯定會(huì)影響語(yǔ)言能力的形成和發(fā)展，它往往是阻礙語(yǔ)言能力發(fā)展的一個(gè)重要的障礙.比如兩向量a=(x1,y1),b=(x2,y2),a∥b?x1y2-x2y1=0，而a⊥b?x1y1+x2y2=0，很多學(xué)生容易混淆兩種位置關(guān)系的等價(jià)條件，像這樣易混的語(yǔ)言形式應(yīng)強(qiáng)化區(qū)分，以保證向量語(yǔ)言的準(zhǔn)確使用.

3.2 重視向量語(yǔ)言的理解和轉(zhuǎn)化

由于向量語(yǔ)言具有高度的抽象性，所以在具體應(yīng)用時(shí)，必須轉(zhuǎn)化為具體、形象的可操作性語(yǔ)言.這是向量語(yǔ)言能力的關(guān)鍵因素.而轉(zhuǎn)化建立在對(duì)向量語(yǔ)言含義有深刻理解的基礎(chǔ)之上.以下列舉一些向量語(yǔ)言與圖形、坐標(biāo)及方程語(yǔ)言間的常見轉(zhuǎn)化[2].

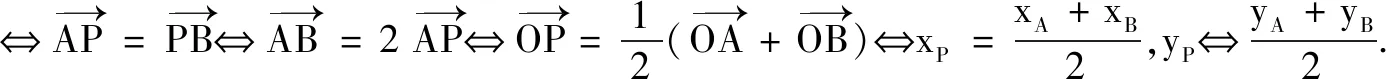
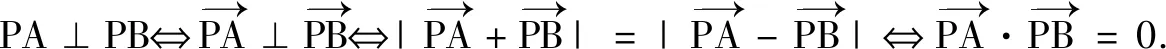
(3)以線段AB為直徑的圓過(guò)點(diǎn)P?(xA-xP)(xB-xP)+(yA-yP)(yB-yP)=0.

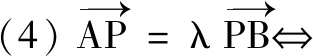
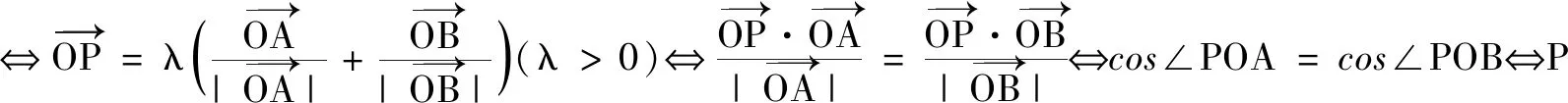
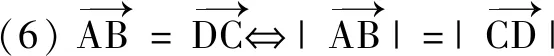
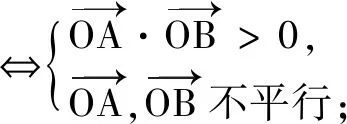
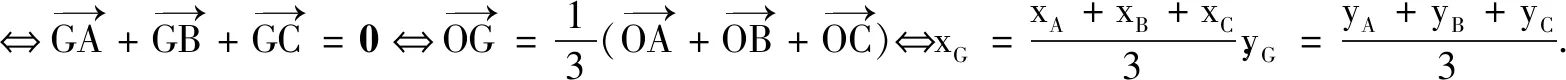
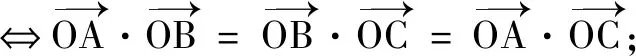
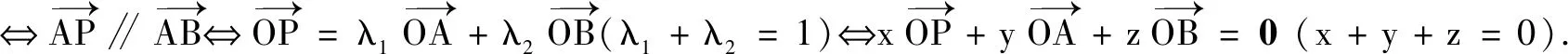
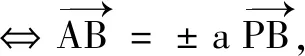
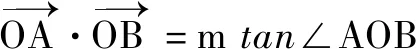
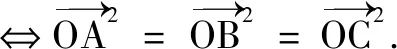
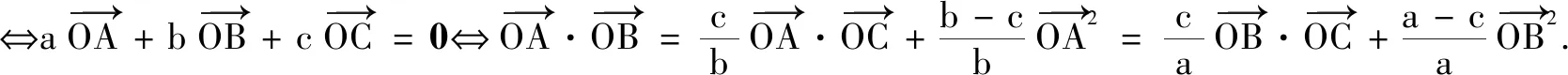
以上轉(zhuǎn)化說(shuō)明向量語(yǔ)言具有豐富的內(nèi)涵，但在具體應(yīng)用的時(shí)候，適當(dāng)?shù)男问阶兓鞘钟斜匾?由于向量語(yǔ)言是抽象簡(jiǎn)潔的(這也是向量語(yǔ)言美的體現(xiàn))，往往給理解帶來(lái)麻煩，此時(shí)可以將其轉(zhuǎn)換為圖形語(yǔ)言，便于理解向量語(yǔ)言所描述的數(shù)量和位置關(guān)系，進(jìn)而把問(wèn)題直觀化.同時(shí)，向量語(yǔ)言有廣泛的應(yīng)用性.做為工具，它最重要的價(jià)值體現(xiàn)在，用數(shù)的方法處理幾何圖形問(wèn)題.可見，將向量語(yǔ)言轉(zhuǎn)化為坐標(biāo)和方程語(yǔ)言是十分必要的，這有利于進(jìn)一步用解析法處理幾何問(wèn)題.

3.3 注重向量語(yǔ)言的表達(dá)

數(shù)學(xué)表達(dá)能力是數(shù)學(xué)語(yǔ)言能力的最直接的體現(xiàn)，華羅庚先生曾教育中學(xué)生在數(shù)學(xué)表達(dá)上要“想得清楚，說(shuō)得明白，寫得干凈”[3].在教育實(shí)踐中我們發(fā)現(xiàn)，向量語(yǔ)言表達(dá)得準(zhǔn)確與否是影響解題能力的關(guān)鍵.如在向量運(yùn)算的教學(xué)中，對(duì)于實(shí)數(shù)與向量的積一定不能簡(jiǎn)稱為向量的數(shù)量積，它們是明顯不同的兩個(gè)概念.再如，向量a在向量b上的投影與射影，一字之差卻有著質(zhì)的區(qū)別.投影是個(gè)數(shù)量，而射影卻是幾何圖形.對(duì)于這些概念的語(yǔ)言描述，應(yīng)該做到準(zhǔn)確描述，正確使用.另外，還有些問(wèn)題也值得關(guān)注：增減條件、不設(shè)先用、以圖代算、語(yǔ)意含糊等[3].對(duì)于這些問(wèn)題，可以針對(duì)平時(shí)課堂發(fā)言、課后作業(yè)和考試練習(xí)中暴露出的問(wèn)題及時(shí)糾正，認(rèn)真講評(píng)，保證言必有據(jù)， 培養(yǎng)學(xué)生良好的語(yǔ)言習(xí)慣，促進(jìn)表達(dá)能力的提高；經(jīng)常要求學(xué)生口述某些數(shù)學(xué)內(nèi)容， 如公式、結(jié)論以及推導(dǎo)過(guò)程，以促進(jìn)學(xué)生學(xué)習(xí)、記憶、理解、應(yīng)用向量語(yǔ)言.

3.4 強(qiáng)化向量語(yǔ)言的應(yīng)用意識(shí)

平面向量的圖形內(nèi)涵及其豐富的運(yùn)算性質(zhì)決定了向量語(yǔ)言具有廣泛的適應(yīng)性，它可以滲透到中學(xué)數(shù)學(xué)的各個(gè)主干知識(shí)中去.除此之外，它在物理中也有體現(xiàn).以下僅就題目設(shè)置與向量語(yǔ)言的關(guān)系舉例說(shuō)明.

·三角中的向量語(yǔ)言

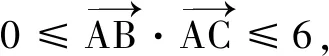
說(shuō)明 用向量語(yǔ)言描述三角形中元素的特征.

·函數(shù)中的向量語(yǔ)言

例2(2006·湖北理16題)設(shè)函數(shù)f(x)=a·(b+c)，其中向量a=(sinx,-cosx)，b=(sinx, -3cosx)，c=(-cosx,sinx)，x∈R.(1)求函數(shù)f(x)的最大值和最小正周期；(2)將函數(shù)f(x)的圖象按向量d平移，使平移后得到的圖象關(guān)于坐標(biāo)原點(diǎn)成中心對(duì)稱，求長(zhǎng)度最小的d.

說(shuō)明 向量語(yǔ)言構(gòu)造函數(shù)，考查函數(shù)圖象的變換，解決問(wèn)題的關(guān)鍵是合理使用向量語(yǔ)言.

·數(shù)列中的向量語(yǔ)言

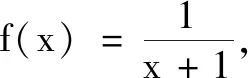
說(shuō)明 以函數(shù)為背景，用向量語(yǔ)言和向量的方法構(gòu)造數(shù)列.

·不等式中的向量語(yǔ)言

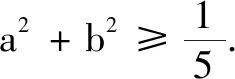
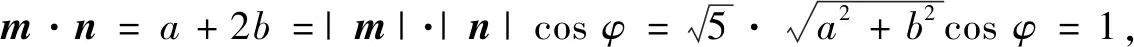
說(shuō)明 巧妙地構(gòu)造向量，讓a+2b具有明確的向量意義，使抽象的不等式證明變得直觀.

·解析幾何中的向量語(yǔ)言

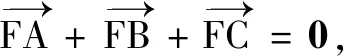
A.9 B.6 C.4 D.3

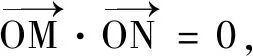
說(shuō)明 用向量語(yǔ)言確定曲線上點(diǎn)的位置時(shí)，關(guān)鍵是深刻理解向量語(yǔ)言的內(nèi)涵，將其轉(zhuǎn)化為點(diǎn)的特征.

·線性規(guī)劃中的向量語(yǔ)言

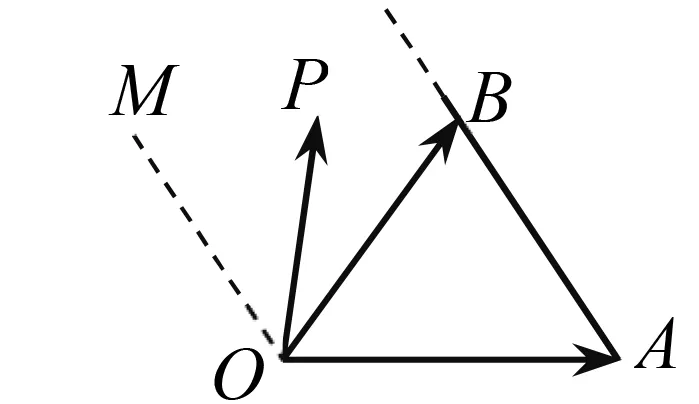
圖2

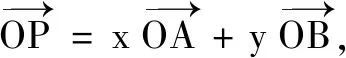
說(shuō)明 本題以平面向量為載體，在考查平面向量運(yùn)算法則的同時(shí)，著重考查在給定區(qū)域內(nèi)的點(diǎn)的線性表示問(wèn)題.由于題型設(shè)計(jì)新穎，且所給圖形不一般，所以處理起來(lái)難度較大.

·物理中的向量語(yǔ)言

教材中在引入向量的概念時(shí)就列舉了大量的物理中的力、速度、加速度等實(shí)際背景，在向量運(yùn)算的引入時(shí)分別用了力的合成和分解以及功為背景.所以在物理中使用向量語(yǔ)言是自然的，這也是數(shù)學(xué)應(yīng)用的體現(xiàn)，是學(xué)科整合的要求.現(xiàn)列舉一例來(lái)說(shuō)明問(wèn)題.

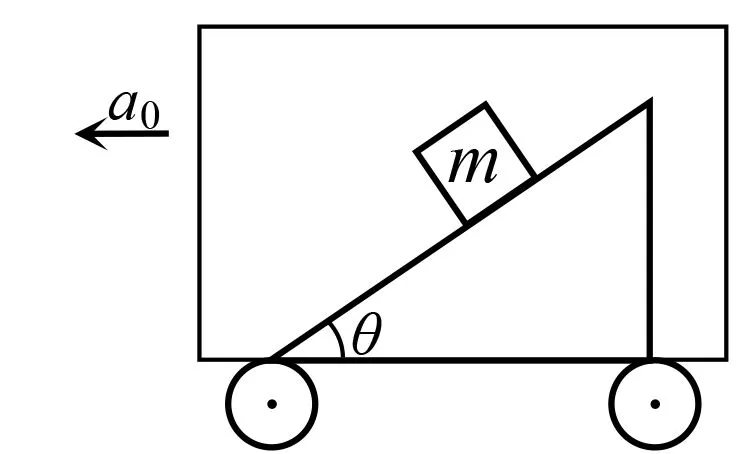
圖3

例8如圖3,在加速行駛的火車上固定一個(gè)斜面，斜面的傾角為θ，有一物體置于斜面上.若火車加速度小于某一值a0， 物體就會(huì)下滑.設(shè)物體質(zhì)量為m，物體與斜面間的摩擦因數(shù)為μ，求a0.[4]

解設(shè)物體的重心為點(diǎn)O，以過(guò)點(diǎn)O與斜面平行的直線為x軸，與斜面垂直的直線為y軸建立坐標(biāo)系.設(shè)重力為G，斜面對(duì)物體的支持力為N，摩擦力為f，慣性力為F，則|G|=mg, |f|=|N|μ, |F|=ma0.由平衡原理列方程：

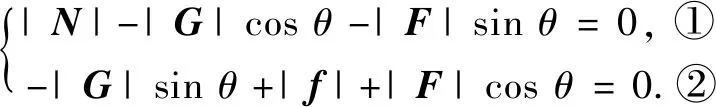
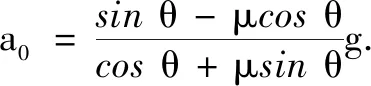
說(shuō)明 借助向量語(yǔ)言，利用向量的思想方法解決物理問(wèn)題.

3.5 注意向量語(yǔ)言能力形成的幾種障礙

向量語(yǔ)言能力的提高是循序漸進(jìn)的過(guò)程，應(yīng)該有計(jì)劃、有步驟，由簡(jiǎn)單到復(fù)雜，由低級(jí)到高級(jí)，由靜止到運(yùn)動(dòng)組織教學(xué).需要學(xué)生通過(guò)讀向量、寫向量、說(shuō)向量、閱讀理解、交流討論等方式，逐步提高正確運(yùn)用向量語(yǔ)言的能力.在這個(gè)過(guò)程中，以下幾種常見的語(yǔ)言障礙值得我們注意.

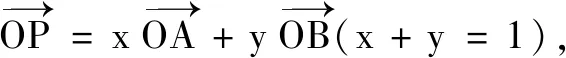
·向量語(yǔ)言轉(zhuǎn)換障礙 它是指學(xué)生在不同表達(dá)形式的向量語(yǔ)言之間，或在向量語(yǔ)言和其他形式的數(shù)學(xué)語(yǔ)言進(jìn)行轉(zhuǎn)換時(shí)產(chǎn)生了困難.如前所述，在向量的教學(xué)過(guò)程中，應(yīng)該加強(qiáng)語(yǔ)言間轉(zhuǎn)化的訓(xùn)練，形成較強(qiáng)的語(yǔ)言轉(zhuǎn)化能力是向量語(yǔ)言能力的核心問(wèn)題.

·向量語(yǔ)言操作障礙 它是指學(xué)生在運(yùn)用向量語(yǔ)言進(jìn)行推理 、運(yùn)算的過(guò)程中出現(xiàn)錯(cuò)誤的現(xiàn)象.例如，很多學(xué)生通常會(huì)犯a·b=a·c?b=c和a·b=0?b=0或a=0的錯(cuò)誤.這首先說(shuō)明了對(duì)向量基本運(yùn)算的理解不夠透徹，其次也體現(xiàn)了對(duì)向量語(yǔ)言本質(zhì)的內(nèi)涵的理解不夠.