基于ABAQUS非飽和膨脹土邊坡降雨入滲分析

饒 鴻，王金淑，吳 光

(西南交通大學，四川成都 611756)

降雨是影響邊坡穩定性的主要因素之一，研究降雨入滲過程邊坡穩定性的變化及邊坡內部滲流場和應力場的變化規律具有重大意義[1]。

Fredlund[2]等應用Galerkin有限元法模擬暴雨條件的土坡滲流及穩定性分析；吳宏偉[3]等針對香港地區典型非飽和土邊坡模擬分析多種因素影響下邊坡滲流場的變化規律及穩定性評價；李炎隆[4]等基于ABAQUS有限元軟件結合降雨入滲的邊界條件,進行降雨入滲邊坡的穩定性分析。降雨入滲非飽和土邊坡，土體吸力降低抗剪強度下降，進而影響邊坡穩定性。根據非飽和土力學：基質吸力是影響非飽和土性質的主要參數之一，非飽和土的強度、變形和滲透性等都與非飽和土吸力值密切相關[5]。本文以貴州省某地區膨脹土為研究對象，結合室內實驗數據建立非飽和土土水特征曲線模型，基于ABAQUS有限元軟件建立邊坡模型，導入膨脹土土水特征曲線公式，考慮降雨過程非飽和土的吸力變化和強度衰減分析降雨入滲下非飽和膨脹土邊坡的滲流場變化和流固耦合分析，探究降雨過程邊坡滲流場、位移場、穩定性的變化規律。

1 計算原理及方法

1.1 飽和-非飽和理論

降雨在非飽和土中滲流滿足質量守恒定律，以達西定律為基礎結合滲流過程中流體質量守恒推導出以基質勢為因變量的滲流控制方程[3]：

(1)

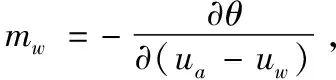
(1)初始條件：一般在模型中指定初始地下水位或進行穩態計算定義滲流初始條件。

h(x,y,t)=h(x,y,t0)

(2)

(2)定水頭邊界條件：在降雨入滲邊界上各點的水頭在某時間段內是已知的。

h|Γ1=h1(x,y,t)

(3)

(3)流量邊界條件：單位面積流量q可以被賦予到邊界某部分，或者水頭函數的法向導數被賦予到邊界。

(4)

1.2 流固耦合方程

根據虛功原理和質量守恒定理獲得滲流場與應力場耦合的平衡方程和滲流連續性方程，再通過劃分邊坡滲流場為有限單元組合，結合邊界條件采用Galerkin有限元解法將坡面方程與滲流控制方程聯立求解，推導流固耦合方程[1]：

(5)

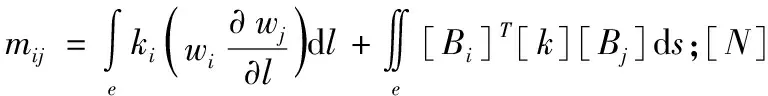
1.3 非飽和土抗剪強度公式

國內外眾多學者基于土體強度試驗數據提出了大量非飽和土的抗剪強度理論公式，應用較廣的是Fredlund基于Mohr-Coulumn準則推導出的雙應力狀態變量理論公式[6]：

τf=c′+(σ-ua)tanφ′+(ua-uw)tan(φb)

(6)

式中：τf為非飽和土抗剪強度；c′為有效粘聚力；φ′為有效內摩擦角；ua為孔隙氣壓力；uw為孔隙水壓力；(σ-ua)為凈法向應力；(ua-uw)為基質吸力；φb為受基質吸力影響的摩擦角，tan(φb)表示基質吸力對應抗剪強度曲線的斜率。

根據Fredlund強度理論[5]，抗剪強度受凈法向應力和基質吸力影響。在有限元分析中常常將孔壓氣壓力設置為零，故非飽和土強度主要受基質吸力的影響，獲得基質吸力是研究非飽和土強度及邊坡穩定性的關鍵。

1.4 強度折減方法

本文應用強度折減法計算降雨入滲后邊坡的穩定系數，通過人為假定不同折減系數對抗剪強度指標進行折減，削弱土體的抗剪強度使單元應力達到屈服或超出屈服面，邊坡產生塑性變形；當其內部形成連續塑性貫通面或特征部位產生突變位移，表征邊坡失穩破壞。

cm=c/Fs

φm=arctan(tanφ/Fs)

(7)

式中：Fs為強度折減系數；c、φ為實際抗剪強度指標；cm、φm為人為折減后的抗剪強度指標。

實現方法：提取邊坡降雨入滲分析后單元節點的孔隙水壓力，轉換為荷載施加到節點上，定義折減系數為場變量，實現邊坡的強度折減，計算邊坡穩定系數。

2 有限元計算模型

2.1 土水特征曲線模型

根據非飽和土力學[5]：非飽和土的基質吸力是伴隨土體含水量變化而變化的，可應用土水特征曲線表征含水量與基質吸力的函數關系。本文應用濾紙法測量膨脹土的基質吸力。濾紙法將濾紙作為測量傳感器，將濾紙直接接觸土樣，通過測量濾紙的平衡含水量結合濾紙的率定曲線計算出土體的基質吸力[7]。

首先配置不同含水率的膨脹土樣，將其制備成標準環刀試樣(同一含水率兩組試樣)，選擇國產“雙圈”牌NO.203濾紙與環刀試樣直接接觸，恒溫環境靜置10天，測量濾紙含水量及土試樣含水率，應用濾紙的率定公式[8](公式8)計算出不同含水率對應基質吸力值(圖1實測值點)。

lg(hm)=-0.076wfp+5.493,wfp≤47%

lg(hm)=-0.012wfp+2.470,wfp>47

(8)

基于濾紙法試樣數據，結合Fredlund-Xing[5]數學模型經驗公式(公式9)分析土體體積含水率與基質吸力的相關關系，應用Matlab程序計算出Fredlund-Xing模型的參數(表1)，得到體積含水率與基質吸力的擬合公式，繪制膨脹土的土水特征曲線(圖1擬合曲線)。

(9)

式中：θ為非飽和土的體積含水率；θs為飽和體積含水率；h為基質吸力；hr是與土樣的殘余含水率θr的基質吸力相關的量；α、m、n為與土水特征曲線形態相關參數(表1)。

表1 Fredlund-Xing模型參數

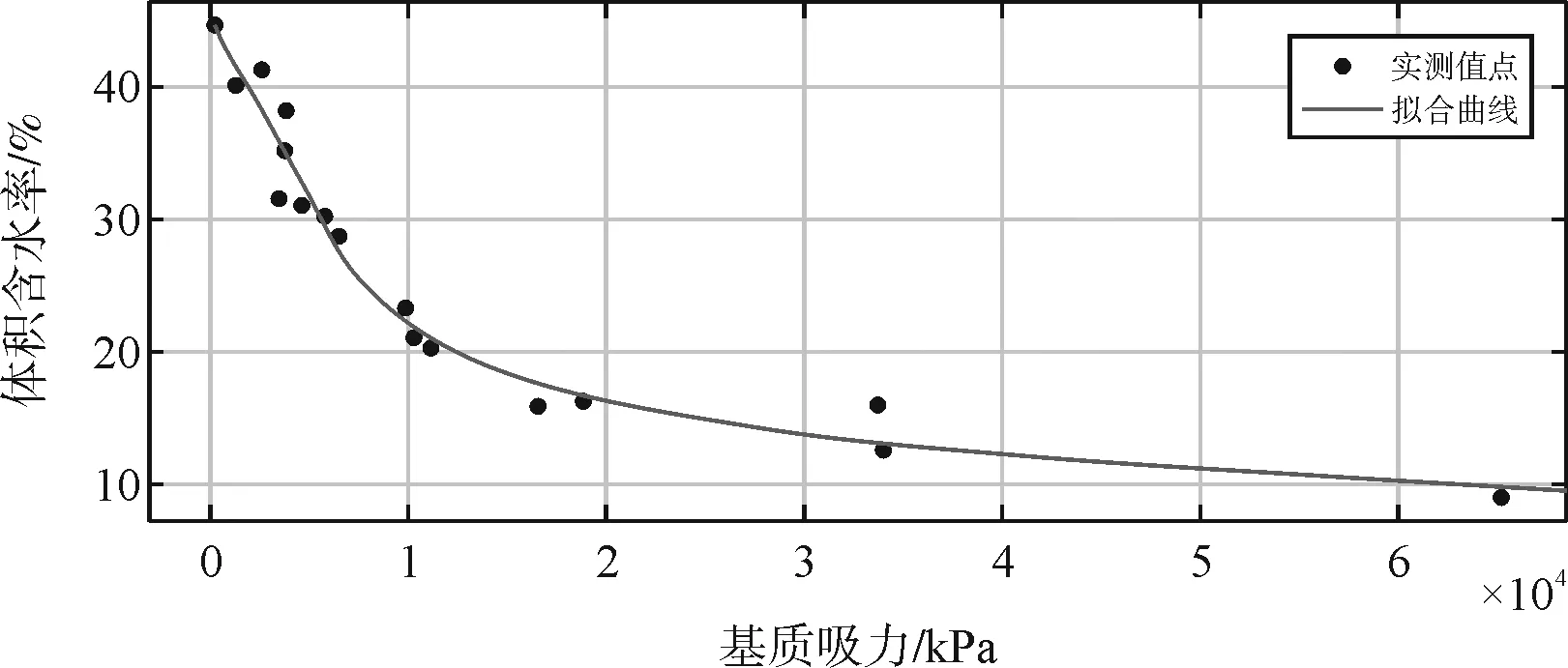
圖1 膨脹土土水特征曲線

2.2 邊坡數值模型

邊坡為非飽和膨脹土邊坡，有限元模型如圖2所示。

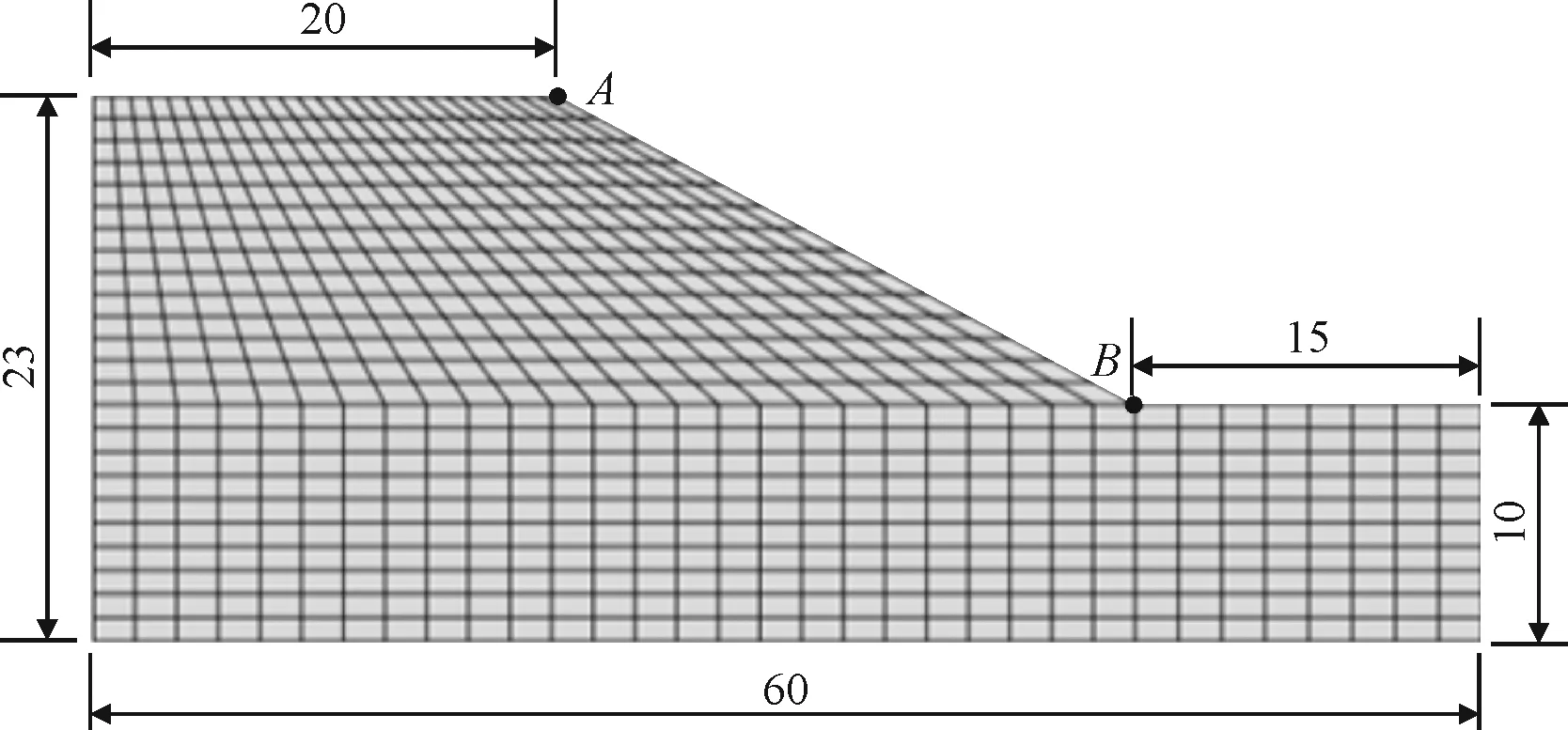
圖2 非飽和膨脹土邊坡模型示意(單位：m)

初始條件：底面設置為雙向(水平向、豎向)約束邊界，側面設置為水平向約束邊界，其余為自由邊界；左側邊界地下水位為10m，右側邊界地下水位為8m，邊坡頂面、臨空面及地表設置為降雨入滲邊界。

降雨條件：降雨強度為0.01m/h，降雨歷時為24h，降雨全部入滲。土體材料為理想彈塑性模型，遵循Mohr-Column強度準則。具體材料參數如表2。

表2 土體材料參數

3 計算結果分析

3.1 滲流場分析

降雨入滲非飽和膨脹土邊坡后，土體含水率增加，孔隙水壓力發生顯著變化。圖3為邊坡降雨前后孔隙水壓力分布云圖。降雨前，邊坡初始水位以下為飽和區，土體孔壓為正；初始水位以上為非飽和區，土體孔壓為負由水位面向坡頂線性減小；降雨24h后，邊坡非飽和區逐漸減小，飽和區逐漸擴大發展至整個邊坡，地下水位發生顯著抬升。取邊坡頂部(A點)和坡腳(B點)探究非飽和土孔隙水壓力變化規律。圖4為降雨過程邊坡孔隙水壓力變化曲線：降雨初期，邊坡表層土體孔壓迅速增加，雨水向邊坡內部滲流，降雨5h左右，坡腳孔壓為零土體率先達到飽和，表明雨水首先在坡腳處匯集；伴隨降雨持續土體孔壓也持續遞增，坡腳土體孔壓變化率大于坡頂，降雨中后期，坡腳土體達到最大孔壓值，受土體強度降低變形增大影響，土體孔壓開始減小并逐漸趨于穩定；坡頂土體孔壓持續增加，降雨20h左右，坡頂孔壓為零，土體達到飽和，孔壓逐漸趨于穩定。

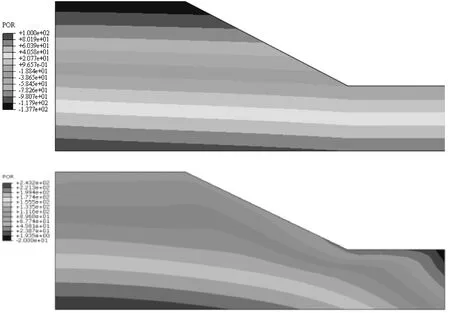
圖3 降雨前后孔壓分布云圖

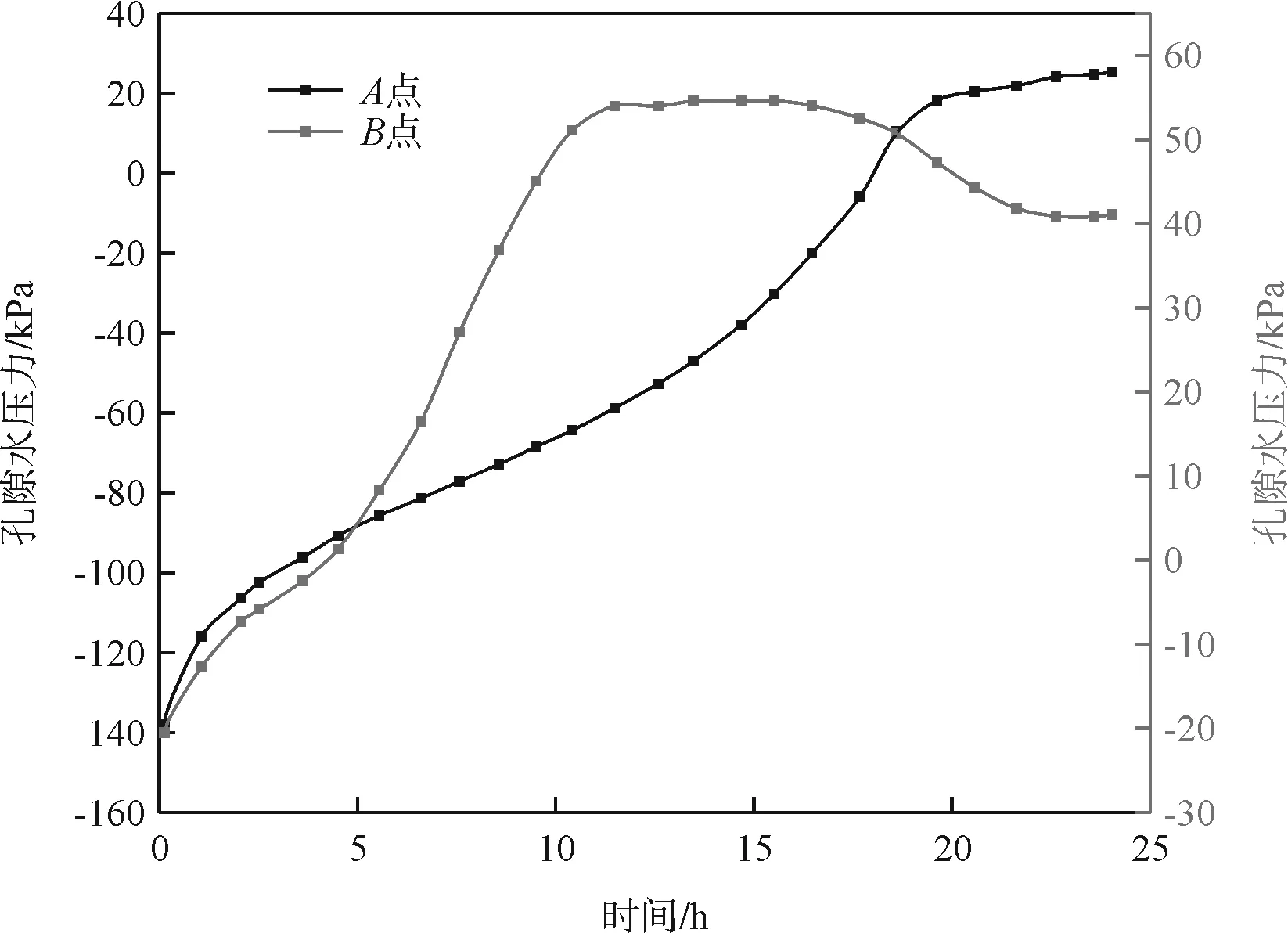
圖4 降雨過程邊坡孔壓曲線

3.2 位移場分析

取坡腳(B點)土體為位移監測對象。降雨過程土體位移曲線如圖5所示，土體位移伴隨降雨歷時遞增，土體位移變化率由小到大緩慢增加。根據土體位移曲線斜率變化規律，以降雨12h為節點將位移曲線劃分為穩定小變形階段與非穩定大變形階段：(1)穩定小變形階段：曲線較平緩斜率小，土體位移很小，伴隨降雨時間增長變形緩慢遞增，以小變形為主；(2)非穩定大變形階段：曲線較陡斜率較大，土體位移迅速增加，位移變化率較大，土體發生不可逆大變形，降雨結束后邊坡總體位移較大，水平位移大于豎向位移，表明降雨引發了邊坡失穩破壞。結合降雨過程土體總體位移矢量圖(圖6)分析，邊坡內部發育圓弧形滑動面，土體順滑動面向外滑移，以水平位移為主，上部土體率先產生大變形，推移中下部土體向坡外移動，邊坡具備典型推移式滑坡特征。

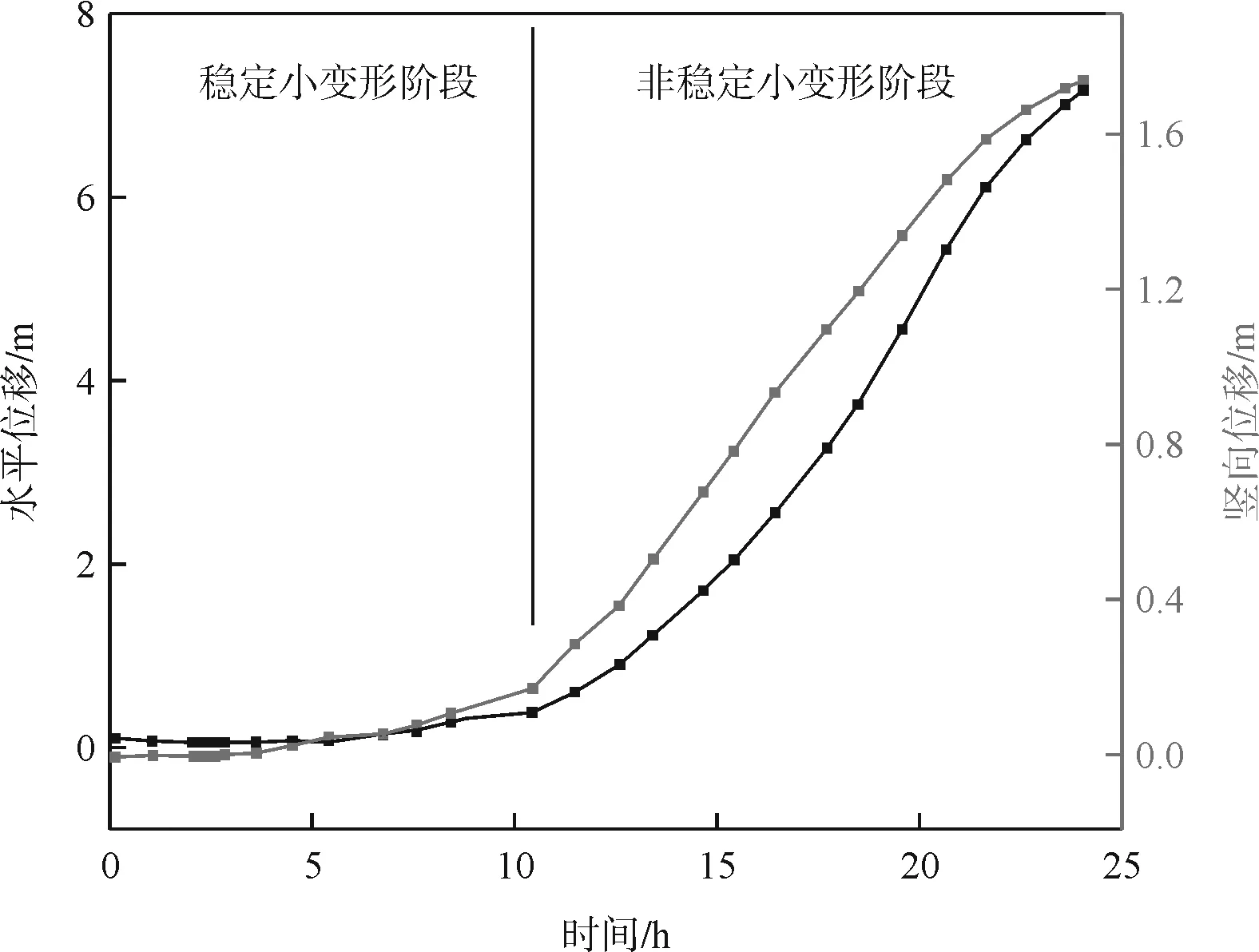
圖5 降雨過程土體位移曲線

圖6 降雨結束土體總位移矢量

3.3 穩定性分析

降雨過程，土體強度受基質吸力變化而降低，邊坡的穩定系數逐漸減小，穩定性降低。圖7為膨脹土邊坡的塑性面發展示意圖。降雨初期坡腳土體率先達到飽和，土體基質吸力迅速減小，強度減小至較小值，坡腳處首先產生塑性變形見圖7(a)，穩定系數為1.25；伴隨降雨持續，邊坡飽和區擴大而地下水位抬升，邊坡后緣水位高于坡腳水位，內部雨水以向坡腳滲流為主，坡腳土體受水平向滲流力作用，有效應力逐漸減小，塑性變性由坡腳逐漸向內部頂部發展，降雨12h左右，塑性面發展至坡頂，邊坡內部形成圓弧形貫通面見圖7(b)，穩定系數為0.994，邊坡開始失穩滑動；降雨結束后，邊坡整體失穩破壞，發生推移式滑坡，滑面形式為中心圓，穩定系數為0.845，見圖7(c)。

(a)降雨5h

4 結論

(1)本文應用濾紙法實驗，結合Fredlund-Xing數學經驗公式，推導出非飽和膨脹土的土水特征曲線模型，繪制了土水特征曲線，可供實際工程參考。

(2)持續降雨過程，雨水首先在坡腳處匯集，再逐漸向邊坡內部入滲。邊坡失穩的主因是地下水位差異抬升，邊坡內部雨水向坡腳滲流，受水平向滲流力作用土體有效應力減小；滲流區域土體軟化，基質吸力減小而強度降低，內部發育圓弧形滑動面，土質邊坡產生推移式滑動。