井灌區灌溉可應用機井的空間布局優化探究

滕 凱

(海城市水利事務服務中心，遼寧 海城 114200)

如何在某特定區域內合理部署若干灌溉機井，系為機井空間布局優化計算的重點環節所在。一般此類問題的研究方法主要有三種，一是多邊形格網法，二是電荷排斥模擬方法，三是優化算法結合一定準則(目的函數)法。因為井灌區存在機井限建區，而且是典型的非規則多邊形區域，倘若選用第一種方法，則通常無法保證井數實現均勻分布；而第二種方法還未付諸于實踐，與其相關的文獻資料相對比較匱乏；只有第三種方法不僅理論基礎夯實，而且在物流配送、村鎮土地空間布局等多領域均實現了廣泛應用。所以本研究決定重點通過此方法來實現合理布局機井的計算和設計目的，確定案例區域相對優化的布井數量與區域機井分布狀態，以為區域灌溉機井的空間布局工程應用提供計算技術參考。

1 研究區概況

本文案例對象系位于華北某縣的覆蓋2鎮12村的井灌區。經實地勘察與資料查詢后得知，該區域系為典型的平原地區，西北部地勢偏高，東南部地勢偏低，海拔差不是很大。水文地質系為第四系地質，主要以灰巖為主，其間巖石裂斷帶和裂縫發育，有利于地下水潛藏。區域位于暖溫帶，屬半濕潤大陸性季風氣候區，四季分明，雨熱同期，春季少雨干燥，夏季多雨高溫，秋季涼爽依然，冬季低溫少雪。該區域機井現狀具體見表1。

本區已投入使用的機井均由當地村民出資建設，由于規劃不得當，致使機井分布欠缺合理，一些區域在農忙時時常出現達不到預期要求出水量問

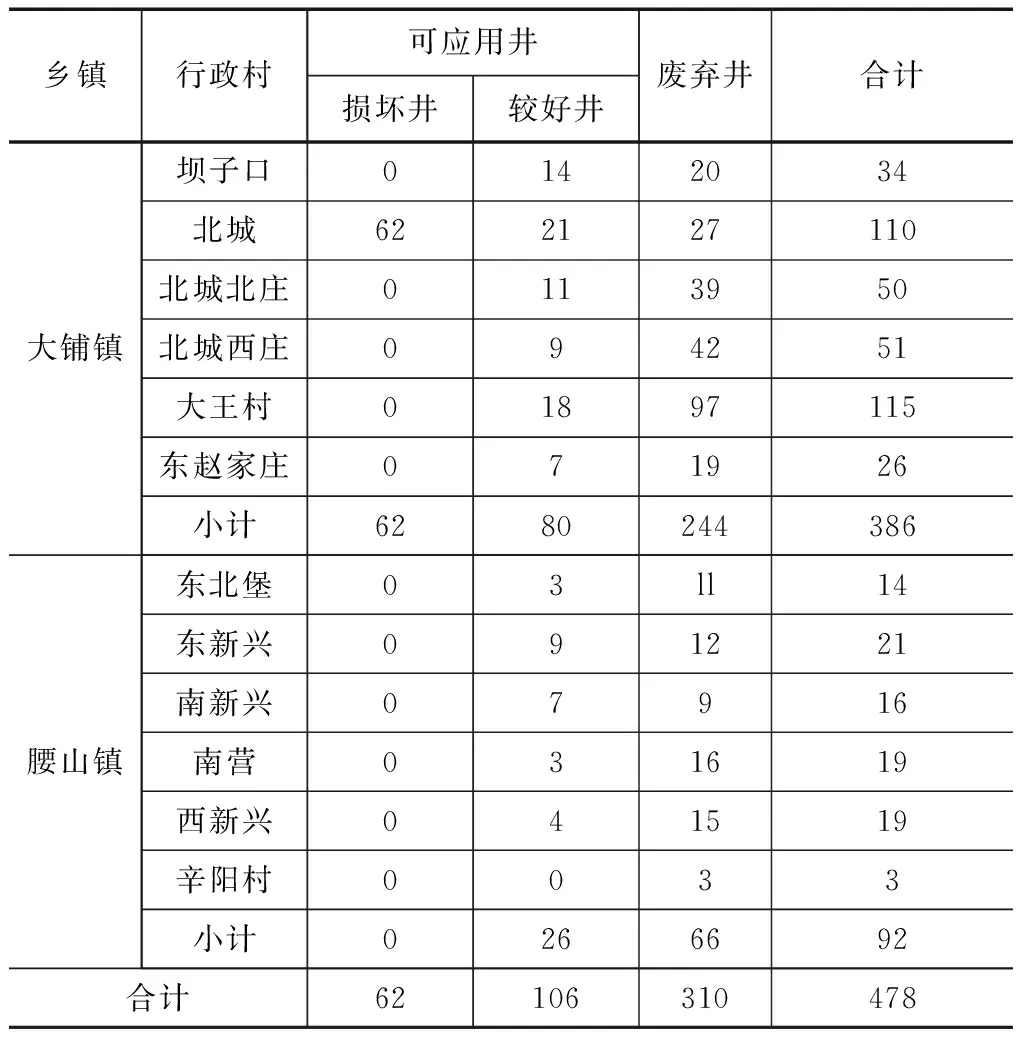
表1 井灌區機井現狀基本統計表(眼)

題，該情況的出現不僅延誤作物灌溉最佳時機，還不利于莊稼正常生長，直至最終形成減產甚至無產的局面。

井灌區灌溉可應用機井密度統計分布狀態如圖1所示。

圖1數據揭示，該區灌溉密度基本保持在0.9眼/hm2左右，通過倒數推算求解發現，單井需灌溉10.92hm2土地，遠高于當前的3.59hm2。很明

圖1 井灌區灌溉可應用機井密度統計分布狀態圖

圖2 可應用類井灌區機井灌溉率統計分布狀態圖

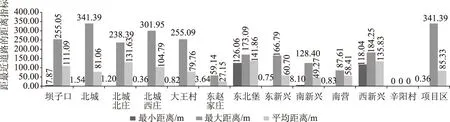
圖3 基于近路距離的可應用類井灌區機井統計分布狀態圖

顯，該區的機井數量不充足，單井灌溉能力己無法切實滿足當前農業需求。

區域可應用類井灌區機井灌溉率統計分布狀態如圖2所示。

圖2數據揭示，區域機井分布過于集中的系數北城村，如果現存機井達到了使用期限而不得不報廢時，局部可選擇的部署空間也相對狹小。雖然其他村落的灌溉率差強人意，機井建設也存在很多問題，但卻為新井建設預留出了足夠大的空間。所以，唯有各村重新優化機井布局方案，才能提高地下水資源的使用率，延遲機井的使用期限。

基于近路距離的可應用類井灌區機井統計分布狀態如圖3所示。

圖3數據揭示，整個井灌區的各行政村的指標數據均存在較大差異，該區的機井灌溉便捷性不夠。造成此現象的原因：一是道路建設不完善；二是井位選取位置不當，與道路間隔太遠。

綜上可知，當前井灌區存在多重問題，最突出的是機井量少、機井遠離道路、井距不合理，由此引發了出水量少、灌溉延遲、地下水利用率過低等問題。就本質上看，導致這些問題發生的根源是機井布局缺乏統一規劃，而且布設隨意性較強。通過實地勘察還發現，研究區的機井建設全由村里人出資，以農戶自打水井為主，并且村民節水觀念不強，忽略了地下水資源的循環使用。所以，要站在新的視角上來部署新井，在提高地下水使用率，合理使用現狀機井，充分考慮現實場景及實際需求的基礎上，通過新建井數的科學計算確定出最理想部署方案。

2 構建優化模型

機井標識通常借助兩要素：一是地理空間坐標，二是屬性值。倘若盲目地調整機井位置，必然會使原有井群布局發生變化，也就不能保證農業灌溉的及時性與便捷性。因此，機井布局的空間有關性是極其重要的，而這就牽扯到了空間抽樣理論的應用。該理論是圍繞如何分布樣本點展開相關研究的，也就是采用優化算法，從有限的樣本點集中，隨機抽取某一子集，使其通過優化處理達到預期要求。很明顯，這是一類組合優化問題，可利用下式表達數學模型：

minf(x)

s.t.g(x)≥0

x∈D

式中，D—樣本點集；X—決策變量；g(x)—約束函數；f(x)—優化準則目的函數。所以，可利用該模型對機井空間布局這一復雜問題進行簡化處理。具體來講就是先抽取出與井數等量的點，再按照限定準則及實際要求進行優化處理，最后確定出最符合要求的的新建井點。

2.1 主要決策變量

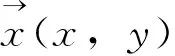
2.2 優化基本準則

機井合理布局不僅能延長機井使用期限，還能提高地下水使用率，形成良好灌溉效益。因此，井群分布一定要合理、均勻。由于現狀機井仍能正常使用，解決農業灌溉問題，所以優化準則的制定與實施務必要與當前機井的布局要求相吻合。

在應用的樣本優化選取準則中，平均最短距離最小化準則(MMSD)最大優勢在于能盡可能地均勻分布采樣點，使任意點與其最鄰近點的間距達到最小值。

所以，本研究選取MMSD當作機井布局優化目的，其優化機理為：研究區內某宜布井點與其最鄰近的新建井點、現用井點間的距離的期望最小值，其計算公式具體如下：

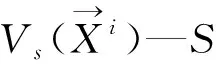
2.3 重點約束條件

(1)井距必要限制：為避免機井同時運作時會互相影響，因此要將新建井點與其最鄰近井點的間隔距離控制在27502m以上。

(2)井數必要限制：由前文表數據可知，機井數量可切實滿足灌水需求，但要消除一切不利灌溉因素。

(3)優先等級限制：優先選取一級宜布井點，在條件達不到的情況下，再考慮其他級別的宜布井點。通過實地勘察與數據統計發現，一、二、三級可部署的井點總量分別為12125、19051、9333個。

3 優化算法與優化布局結果

3.1 選取優化算法

啟發式算法是當前頗受業界人士推崇與青睞的一種優化技術，在空間優化布局問題的解決上具有無與倫比的優勢。當前，使用較為廣泛的空間布局優化方法有很多種，比如遺傳算法(geneticalgorithms，GA)、模擬退火算法(simulatedannealing，SA)等。對這幾種算法的優缺點進行全面分析后發現，SA的優勢更為突出，具體表現為并行搜索能力強、操作便捷、適用范圍廣、受條件限制少。因此，可將此算法應用于本課題研究中，以達到空間優化的目的。

充分利用SA算法優勢的基礎上，結合空間信息的特征，利用Hmax對采樣點的移動空間進行科學界定，以保證經優化處理后的各采樣點均處于最佳部位。Hmax一般被視為相距最遠的兩個點的距離，這樣就能為樣點移動預留出足夠的空間，從而移動到最理想部位。該算法的運行過程具體如下：

Step1：循環頻次n，起始溫度為t；

Step2：計算目的函數φ(S0)，隨機選取一個樣本S0。同時通過特定的隨機擾動，計算目的函數φ(S1)，生成新樣本S1。決定是否接受新樣本主要參考Metropolis準則。

Pc(S0→S1)=

其中，Pc(S0→S1)表示S0替換以S1的概率；

Step3：第2步循環頻次到達n次，實施溫降過程：t=c·t，c∈(0，1)并且近似等于1；

Step4：設置最低溫度tmin，重復前3個步驟，算法在t≤tmin時終止，輸出樣本S0。

3.2 布局優化結果

MATLAB是最近推出的一款主流計算軟件，相較于傳統的C語言和FORTRAN語言，它的功能更強大、優勢更突出，現在被廣泛應用于空間布局優化問題求解領域。因此，在本研究中，筆者利用MATLAB軟件確定出了機井布局優化模型的最優解，也就是新建井點的地理坐標，然后將求取的坐標數據完整、準確地導入ArcGIS中，由此便可生成如圖4所示的井灌區機井空間優化布局結果圖。而井灌區現狀可應用類機井空間分布狀態圖具體可見圖5所示。

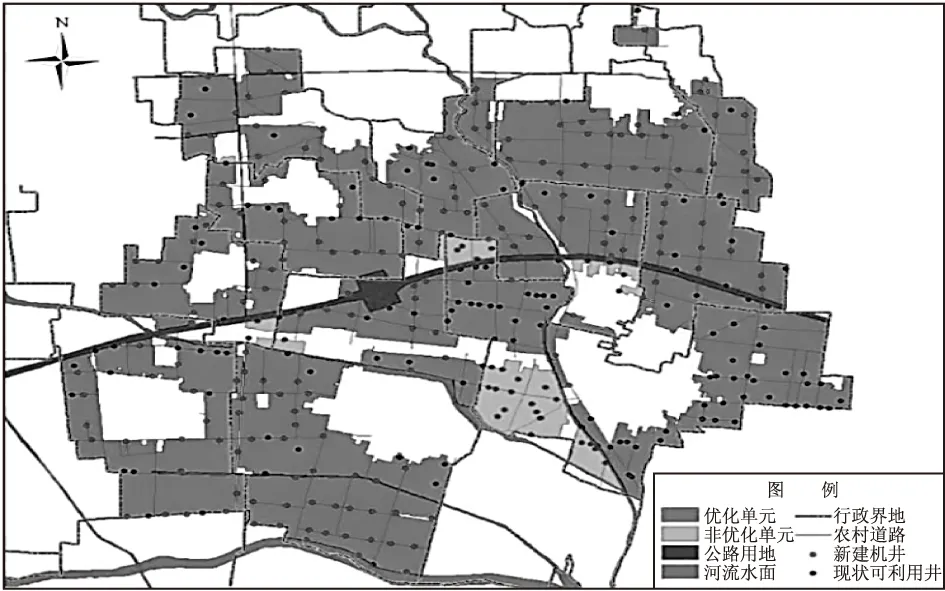
圖4 井灌區優化后的機井空間分布狀態圖

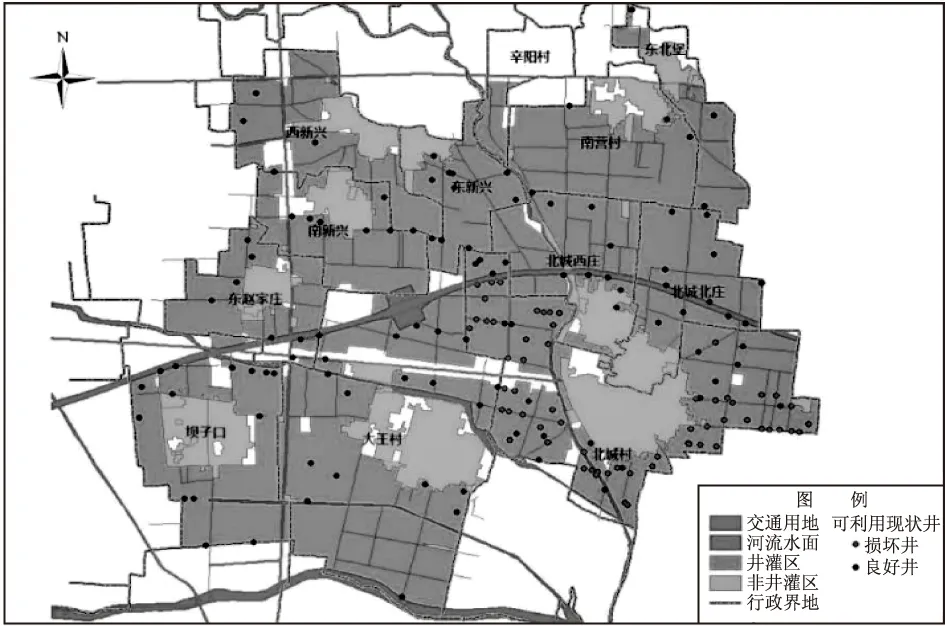
圖5 井灌區現狀可應用類機井空間分布狀態圖

圖4優化后的機井空間分布狀態揭示，新建井點合理地部署在井灌區內，即便這些井泵同時處于工作狀態，也不會產生任何不利影響，由此一來，既提高了水資源利用率，還保證了灌溉的及時性與便捷性。整體來看，新建井點基本靠近道路，簡化了灌溉操作的復雜性，而且處于一級宜布井點區域，也就意味著可忽略二、三級宜布井點。

總而言之，研究區機井空間優化布局結果可滿足現實灌溉需求，也就間接證實了筆者采用的優化布局方法是完全可行的。首先，通過網格單元劃分確定出具體井數，既能解決整體灌區不均勻的難題，還能保證各單元的農作物得到及時灌溉；其次，適宜性評價為井位選取劃分了等級，通過等級劃分合理控制了選取范圍，簡化了中間環節，提高了布井效率；最后，利用優化布井法選取了最佳井點，有效縮短了布設時間。

4 結語

(1)調查分析了案例井灌區現狀可應用類機井的空間分布狀態。

(2)基于主要決策變量、優化基本準則以及重點約束條件，構建了案例井灌區灌溉機井空間優化分布數理計算模型。

(3)基于優化算法計算給出了案例井灌區優化后的灌溉機井空間分布計算成果。雖然不同灌區的區域條件及現存機井分布狀態千差萬別，但本研究的計算實現樣式，可為各井灌區灌溉機井的空間布局優化設計及工程應用提供技術參考。