立體幾何問(wèn)題的正確打開方式：“算”與“思”（下）

曾 榮

傳統(tǒng)“作—證—算”，重在思維，多思少算

例1（2019年高考全國(guó)I 理科卷）如圖，直四棱柱的底面是菱形，E，M，N分別是BC，BB1，A1D的中點(diǎn)．

（1）證明：MN∥平面C1DE；

（2）求二面角A-MA1-N的正弦值．

上期我們已經(jīng)對(duì)例1 作了分析，本期繼續(xù)對(duì)第（2）問(wèn)探索．

圖1

【思路剖析】（綜合幾何法，利用三垂線定理先作出二面角的平面角，再進(jìn)行計(jì)算）

過(guò)點(diǎn)A作AH⊥A1D，垂足為H，連結(jié)MH．

因?yàn)榈酌媸橇庑危螧AD=60°，所以△BCD為等邊三角形，

因?yàn)镋是BC的中點(diǎn)，所以DE⊥BC，所以DE⊥DA．

又AD，D1D?平面ADD1A1，AD∩D1D=D，

所以DE⊥平面ADD1A1，所以DE⊥AH．

又DE，A1D?平面A1DEM，DE∩A1D=D，所以AH⊥平面A1DEM．

所以AH⊥A1M，又AM⊥A1M，AH∩AM=A，所以A1M⊥平面AMH，所以MH⊥A1M，所以∠AMH為二面角A-MA1-N的平面角．

在Rt△A1AD中，因?yàn)锳H⊥A1D，所以AH·A1D=AA1·AD，求得．

所以二面角A-MA1-N的正弦值為．

敲黑板

這里采用傳統(tǒng)“作—證—算”的綜合幾何法求解，“作”后要進(jìn)行嚴(yán)謹(jǐn)?shù)摹白C”．此法運(yùn)算量明顯小于向量坐標(biāo)法．

例2（2018年高考全國(guó)I 文科卷第18題）如圖，在平行四邊形ABCM中，AB AC==3，∠ACM=°90，以AC為折痕將△ACM折起，使點(diǎn)M到達(dá)點(diǎn)D的位置，且AB⊥DA．

（1）證明：平面ACD⊥平面ABC；

（2）Q為線段AD上一點(diǎn)，P為線段BC上一點(diǎn)，且，求三棱錐Q-ABP的體積．

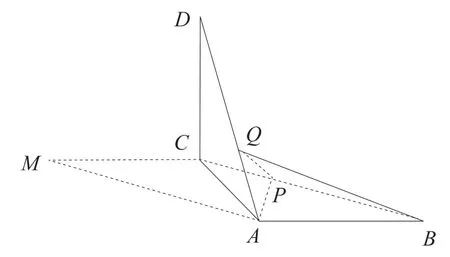
圖2

【思路剖析】

本題是以折疊為背景的幾何問(wèn)題，研究此類問(wèn)題，我們要理清圖形變換前后在數(shù)量關(guān)系和位置關(guān)系上的不變性：

顯性變換：以AC為折痕將△ACM折起，使點(diǎn)M到達(dá)點(diǎn)D的位置數(shù)量關(guān)系的不變性DC CM=，AD AM=位置關(guān)系的不變性CA CM⊥，CA CD⊥，CA AB⊥隱性 △ ≌△CAMCAD可求得AD BC==3 2，BD=3 3，可證得CD BC⊥可結(jié)合AB DA⊥ 證得AB⊥平面CAD，CD⊥平面ABC

第一問(wèn)思路：證平面ACD⊥平面ABC的大方向是證線面垂直．通常的方法有：

思路①通過(guò)證明AB⊥平面ACD來(lái)證平面ACD⊥平面ABC；

思路②通過(guò)證明CD⊥平面ABC來(lái)證平面ACD⊥平面ABC．

第二問(wèn)思路：

思路①直接作圖法，分別求出底面積和高，利用體積公式計(jì)算；

思路②利用體積轉(zhuǎn)換法，將求不規(guī)則幾何體的體積轉(zhuǎn)化為求規(guī)則幾何體的體積．

【規(guī)范解答】

（1）證法一（通過(guò)證明AB⊥平面ACD來(lái)證平面ACD⊥平面ABC）：

因?yàn)樗倪呅蜛BCM是平行四邊形，CM⊥AC，所以AB⊥AC．

又BA⊥AD，AC，AD?平面ACD，AC∩AD=D，所以AB⊥平面ACD．

又AB?平面ABC，所以平面ACD⊥平面ABC．

證法二（通過(guò)證明CD⊥平面ABC來(lái)證平面ACD⊥平面ABC）：

連結(jié)BD．

在Rt△ACD中，DC=AC=3，所以．

在Rt△ABC中，AB=AC=3，所以．

在Rt△ABD中，，AB=3，所以．

在△BCD中，，所以．所以CD⊥BC．

又CD⊥AC，AC，BC?平面ABC，AC∩BC=C，所以CD⊥平面ABC．

又CD?平面ACD，所以平面ACD⊥平面ABC．

（2）解法1（直接作圖法）

過(guò)點(diǎn)Q作QE⊥AC，垂足為E，則QE∥CD．

解法2（體積轉(zhuǎn)換法）

設(shè)三棱錐Q-ABP的高為h，因?yàn)椋怨剩?/p>

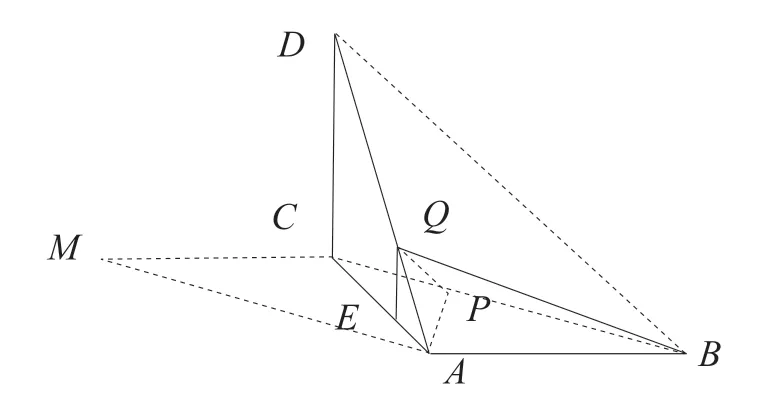
圖3

【歸納提升】

（1）研究線面位置關(guān)系問(wèn)題，同學(xué)們要熟練掌握以下關(guān)系：

（2）求體積問(wèn)題時(shí)，同學(xué)們要善于利用體積之比，將求不規(guī)則幾何體的體積轉(zhuǎn)化為求規(guī)則幾何體的體積，即將一個(gè)高和底面積不易求的幾何體，轉(zhuǎn)化為高和底面積都容易計(jì)算的幾何體．善于轉(zhuǎn)化，可使問(wèn)題越變?cè)胶?jiǎn)單．

解決立體幾何證明和計(jì)算問(wèn)題，需要同學(xué)們根據(jù)自己的學(xué)習(xí)基礎(chǔ)，靈活地選用綜合幾何法和向量坐標(biāo)法．但無(wú)論采用哪種方法，都需要遵循“解而優(yōu)則選”的原則，多思少算，達(dá)到事半功倍的效果．

（“小試牛刀”見第48 頁(yè)）