偏心磁極永磁電機(jī)氣隙磁密解析計(jì)算方法研究

趙國(guó)新　張宇　葛紅巖　劉勇　白保東

摘 要：對(duì)于表貼式永磁電機(jī)，為了獲得良好的電動(dòng)勢(shì)波形，降低齒槽轉(zhuǎn)矩，電機(jī)往往會(huì)采用偏心型磁極來(lái)優(yōu)化氣隙磁密波形，使氣隙磁密波形盡量正弦分布。雖然有限元法可以對(duì)氣隙磁密進(jìn)行計(jì)算、求解，但電機(jī)建模、有限元求解消耗時(shí)間較長(zhǎng)，在工程應(yīng)用和電機(jī)的初步設(shè)計(jì)中有一定的局限性。為了研究計(jì)算偏心型磁極電機(jī)氣隙磁密波形，本文首先根據(jù)二維電磁場(chǎng)理論，建立永磁電機(jī)數(shù)學(xué)模型，采用解析計(jì)算方法分別計(jì)算了常規(guī)等厚度瓦片型磁極和偏心型磁極電機(jī)氣隙磁密的分布;然后將計(jì)算結(jié)果與有限元仿真結(jié)果進(jìn)行了對(duì)比，誤差不超過(guò)4%，驗(yàn)證了計(jì)算方法的正確性。最后通過(guò)對(duì)已制成的3臺(tái)樣機(jī)進(jìn)行實(shí)驗(yàn)并與計(jì)算結(jié)果進(jìn)行對(duì)比，誤差在5%以?xún)?nèi)，驗(yàn)證了該方法的廣泛適用性。

關(guān)鍵詞：偏心磁極;氣隙磁密;解析法;等效面電流法;有限元;永磁電機(jī)

DOI：10.15938/j.emc.2020.06.004

中圖分類(lèi)號(hào)：TM 351文獻(xiàn)標(biāo)志碼：A 文章編號(hào)：1007-449X（2020）06-0024-09

Prediction of flux density distribution inpermanent magnet motor with eccentric magnetic pole

ZHAO Guo-xin1， ZHANG Yu1，2， GE Hong-yan2， LIU Yong2， BAI Bao-dong1

（1. School of Electrical Engineering， Shenyang University of Technology， Shenyang 110870，China;

2.Guizhou Aerospace Linquan Motor Co.， Ltd， Guizhou 550003， China）

Abstract：Eccentric magnetic pole is often used in the surface-mount permanent magnet synchronous motor （PMSM）to optimize the air gap flux density distribution and make the electromotive force（EMF） waveform sinusoidal as much as possible in order to obtain an ideal EMF waveform and reduce the cogging torque. Although the finite element analysis（FEA） can be used to solve and calculate the air gap magnetic density， the motor modeling and finite element solution takes a long time， causing limitations in engineering and preliminary design process of the motor. In order to study the air gap magnetic-density waveform， the two-dimensional and mathematical model were used to calculate air gap magnetic field of tile magnetic pole and eccentric magnetic pole. Then the calculation results were compared with the FEA results， and the error does not exceed 4%，which verifies the correctness of the calculation method. Finally three prototypes were tested and compared with the calculated results， and the error is within 5%， which verifies the wide applicability of the method.

Keywords：eccentric magnet pole;air gap flux density;analytical method; surface current method; finite element method; permanent magnet motor

0 引 言

永磁電機(jī)的空載氣隙磁密對(duì)電機(jī)的運(yùn)行特性具有重要的影響，氣隙磁密的諧波分量將會(huì)引起電機(jī)轉(zhuǎn)矩波動(dòng)增加，振動(dòng)增大，同時(shí)也會(huì)增加高次諧波損耗增加而引起電機(jī)溫升過(guò)高等問(wèn)題，所以在電機(jī)設(shè)計(jì)之初就應(yīng)該對(duì)電機(jī)的氣隙磁密進(jìn)行優(yōu)化分析，從而得到較好的氣隙磁密波形。對(duì)于表貼式永磁電機(jī)來(lái)說(shuō)，最常用的方法是采用偏心型磁極使電機(jī)中各處的氣隙長(zhǎng)度不均，從而使電機(jī)的空載氣隙磁密波形更加趨于正弦。

氣隙磁密波形的計(jì)算一般分為解析法和數(shù)值法兩種。解析法是基于麥克斯韋方程組，通過(guò)解算二維磁場(chǎng)中的拉普拉斯方程或者泊松方程來(lái)得到電機(jī)氣隙處的磁密分布;數(shù)值解法則是基于有限元算法，將連續(xù)的模型進(jìn)行離散化再進(jìn)行計(jì)算，具有很高的計(jì)算精確度，對(duì)復(fù)雜模型的適用性更強(qiáng)，但其計(jì)算時(shí)間長(zhǎng)，不適合用于工程實(shí)踐以及電機(jī)初步設(shè)計(jì)中。國(guó)內(nèi)外學(xué)者為了計(jì)算永磁電機(jī)中氣隙磁密的分布做了許多研究，文獻(xiàn)[1]中，對(duì)3種不同充磁方式永磁體產(chǎn)生的氣隙磁密波形進(jìn)行了仿真分析，并得到了不同充磁方式下氣隙磁密的分布規(guī)律;文獻(xiàn)[2]基于保角變換提出了一種時(shí)效計(jì)算方法在頻域下對(duì)永磁電機(jī)空載情況下對(duì)電機(jī)的氣隙磁密進(jìn)行了解算，并通過(guò)有限元法證明了計(jì)算方法的正確性;文獻(xiàn)[3]和文獻(xiàn)[4]基于子域模型計(jì)算方法對(duì)不同極槽配合、不同充磁方式下的表貼式永磁電機(jī)氣隙磁密進(jìn)行了計(jì)算，并通過(guò)有限元分析以及實(shí)驗(yàn)驗(yàn)證，證明了計(jì)算方法的正確性;文獻(xiàn)[5]通過(guò)子域模型法對(duì)徑向以及切向氣隙磁密進(jìn)行了分析計(jì)算，同時(shí)計(jì)算了表貼式永磁電機(jī)的齒槽轉(zhuǎn)矩，并將計(jì)算結(jié)果與有限元分析進(jìn)行了對(duì)比，驗(yàn)證了結(jié)果的正確性;文獻(xiàn)[6]通過(guò)拉普拉斯方程以及泊松方程計(jì)算了在平行充磁下，分塊永磁體的氣隙磁密分布，并與有限元仿真進(jìn)行對(duì)比;文獻(xiàn)[7]提出了一種新型表貼式永磁電機(jī)結(jié)構(gòu)，并通過(guò)仿真對(duì)氣隙磁密波形進(jìn)行了優(yōu)化;文獻(xiàn)[8]分析了表貼式永磁電機(jī)空載時(shí)的磁密分布及諧波分布，并通過(guò)有限元法對(duì)電機(jī)的空載損耗進(jìn)行了分析計(jì)算;文獻(xiàn)[9-11]根據(jù)二維電磁場(chǎng)理論建立了偏心狀態(tài)下永磁無(wú)刷直流電機(jī)氣隙磁密的數(shù)學(xué)模型，計(jì)算了偏心狀態(tài)電機(jī)的磁場(chǎng)分布和性能變化，并通過(guò)仿真和實(shí)驗(yàn)結(jié)果進(jìn)行了驗(yàn)證;文獻(xiàn)[12]通過(guò)解算拉普拉斯方程和泊松方程對(duì)偏心狀態(tài)下的磁場(chǎng)分布進(jìn)行了計(jì)算，并分析了不同偏心距下電機(jī)的不平衡磁拉力分布。上述文獻(xiàn)中的解析法雖然可以得到精確的計(jì)算結(jié)果，但由于計(jì)算公式繁多復(fù)雜，且所研究模型均為等厚瓦片型磁極永磁電機(jī)，并沒(méi)有對(duì)具有偏心型磁鐵的永磁電機(jī)模型進(jìn)行分析計(jì)算。而使用有限元法對(duì)偏心型磁極永磁電機(jī)進(jìn)行計(jì)算時(shí)，為了得到較好的氣隙磁密波形，需要多次建模進(jìn)行分析計(jì)算，耗費(fèi)時(shí)間長(zhǎng)。

為解決上述問(wèn)題，根據(jù)二維電磁場(chǎng)計(jì)算理論建立表貼式永磁電機(jī)的等效數(shù)學(xué)模型，分別對(duì)等厚度瓦片型磁極和偏心型磁極永磁電機(jī)的氣隙磁密進(jìn)行分析計(jì)算，然后通過(guò)有限元算法與驗(yàn)證實(shí)驗(yàn)進(jìn)行對(duì)比，證明了計(jì)算方法的正確性和廣泛適用性。本文所采用的方法具有計(jì)算精度高，與電機(jī)結(jié)構(gòu)參數(shù)聯(lián)系強(qiáng)等特點(diǎn)，適用于工程實(shí)際分析以及電機(jī)優(yōu)化設(shè)計(jì)中。

1 瓦片型磁極氣隙磁密計(jì)算

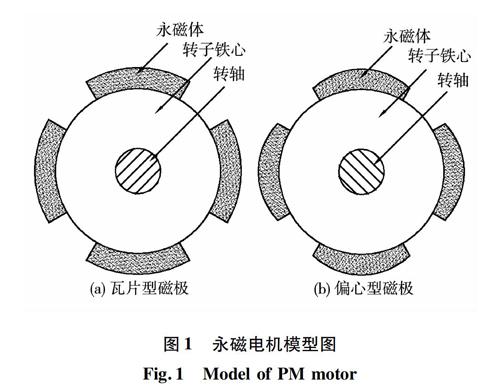
對(duì)于內(nèi)轉(zhuǎn)子表貼式永磁電機(jī)，其磁極形狀如圖1所示。在進(jìn)行分析之前，為了進(jìn)行簡(jiǎn)化計(jì)算，首先做出如下假設(shè)[13]：

1）忽略電機(jī)繞組的端部效應(yīng)，氣隙磁密沿軸向分布相同;

2）鐵磁材料磁導(dǎo)率無(wú)窮大且各向同性;

3）永磁體材料充磁均勻并且具有線性退磁曲線，如衫鈷，釹鐵硼等。

1.1 等厚度瓦片型永磁體的等效數(shù)學(xué)模型

磁介質(zhì)經(jīng)過(guò)外磁場(chǎng)磁化后有了磁化強(qiáng)度，在介質(zhì)體內(nèi)和表面形成束縛電流，對(duì)于均勻磁化的介質(zhì)，束縛體電流為零，僅產(chǎn)生束縛面電流[14-15]。對(duì)于外界而言，永磁體可以用環(huán)繞永磁體表面的一組帶電流的線圈來(lái)等效，如圖2所示。

對(duì)于具有線性退磁曲線的永磁體來(lái)說(shuō)，其面電流密度為

式中Hc為永磁體的矯頑力。

首先對(duì)永磁體等效模型中的單根線圈產(chǎn)生的磁密進(jìn)行分析，如圖3所示。假定氣隙中存在一個(gè)電流為i的理想線圈，線圈兩條邊的跨度角為β，等效線圈所在圓半徑為R3，A點(diǎn)（觀測(cè)點(diǎn)）距離線圈中心的角度為θ。對(duì)于內(nèi)轉(zhuǎn)子表貼式永磁電機(jī)來(lái)說(shuō)，R1和R2分別為永磁體的內(nèi)徑和氣隙內(nèi)徑，R1的內(nèi)部和R2外部分別為電機(jī)的轉(zhuǎn)子和定子鐵心部分，A點(diǎn)相當(dāng)于氣隙處的某個(gè)點(diǎn)。

根據(jù)圖3，在極坐標(biāo)下求解二維磁場(chǎng)的拉普拉斯方程，即可得到單個(gè)線圈在半徑為R2的氣隙圓周上的產(chǎn)生的磁密分布

對(duì)于p對(duì)極的電機(jī)來(lái)說(shuō)，氣隙圓周方向存在2p個(gè)單根線圈，產(chǎn)生的磁密分布為

根據(jù)式（4）求出了2p個(gè)單根線圈的空間磁密分布。對(duì)于等效永磁體模型，只需將構(gòu)成永磁體的每個(gè)線圈單獨(dú)進(jìn)行計(jì)算，再求和即可得到永磁體的空間磁密分布。但由于永磁體充磁方向的不同，其等效數(shù)學(xué)模型不同，空間磁密分布也不相同。

1.2 不同充磁方式下電機(jī)的氣隙磁密

永磁體的充磁方式一般分為徑向充磁和平行充磁兩種，不同的充磁方式將會(huì)造成空間氣隙磁密分布不同，其數(shù)學(xué)模型也有區(qū)別。

徑向充磁方式的永磁體其磁力線平行于半徑方向，數(shù)學(xué)模型如圖4所示。根據(jù)圖4（a），對(duì)式（4）進(jìn)行積分，即可得到徑向充磁永磁體在半徑為R2的圓上所產(chǎn)生的氣隙磁密Brad[16]為

式中：a，b，c分別為電機(jī)定子鐵心內(nèi)徑，永磁體內(nèi)徑和永磁體外徑;α為永磁體所占空間機(jī)械角度。

永磁體采用平行充磁時(shí)，其磁力線的方向總是平行于永磁體的中心線，數(shù)學(xué)模型如圖4（b）所示，可分為兩部分進(jìn)行計(jì)算。其中第一部分與徑向充磁相同，但是其幅值比徑向充磁要小，其表達(dá)式為

第二部分是由圓弧上表面和下表面的等效面電流共同作用而形成的，計(jì)算公式如式（8）～式（10）所示

平行充磁時(shí)氣隙磁密為上面兩部分產(chǎn)生的氣隙磁密之和，即

2 偏心磁極電機(jī)氣隙磁密計(jì)算

根據(jù)上述式（5）～式（11）可求得等厚瓦片型磁極在平行充磁和徑向充磁兩種充磁方式下的氣隙磁密分布規(guī)律。然而對(duì)于不等厚度的偏心型磁極，永磁體的徑向厚度以及氣隙的徑向長(zhǎng)度是關(guān)于空間角度θ（如圖3）的函數(shù)，因此需要進(jìn)行進(jìn)一步分析。

偏心型磁鐵如圖5所示，永磁體的內(nèi)圓是以O(shè)點(diǎn)為圓心，永磁體外圓是以O(shè)1為圓心，兩個(gè)圓心之間的線性距離為h。永磁體的厚度隨著空間角度γ的變化而變化，其所產(chǎn)生的磁動(dòng)勢(shì)在空間上各點(diǎn)也各不相同。永磁體的外徑尺寸與圓心O的距離隨角度γ的變化規(guī)律

永磁體外徑隨空間角度的變化而造成了磁路中永磁體的磁勢(shì)、氣隙的長(zhǎng)度隨空間角度的不斷變化，永磁體內(nèi)部各處的工作點(diǎn)也不相同。通過(guò)有限元仿真計(jì)算得到的一塊偏心型永磁體內(nèi)部磁通密度Bm隨空間角度γ的變化規(guī)律如圖6所示。因此對(duì)于偏心型永磁體來(lái)說(shuō)不能像瓦片型永磁體一樣假設(shè)整塊永磁體的工作點(diǎn)相同，需要對(duì)每一處的工作點(diǎn)單獨(dú)進(jìn)行計(jì)算。

永磁體的工作點(diǎn)是由永磁體自身的退磁曲線和外磁路特性共同決定的，如圖7所示。

永磁電機(jī)外磁路特性由氣隙磁阻和鐵磁材料磁阻共同決定。在電機(jī)中，鐵磁材料的磁阻要遠(yuǎn)遠(yuǎn)小于氣隙磁阻，為簡(jiǎn)化計(jì)算，假設(shè)鐵磁材料的磁導(dǎo)率無(wú)窮大，鐵心磁阻可以忽略，整個(gè)磁路的磁阻僅由電機(jī)氣隙所決定。根據(jù)圖7，經(jīng)過(guò)計(jì)算負(fù)載線和退磁曲線的交點(diǎn)為永磁體的工作點(diǎn)，即

式中：Bw，Hw分別為工作點(diǎn)處的磁密和矯頑力;a為電機(jī)定子內(nèi)徑;c（γ）為永磁體外徑，可以通過(guò)式（12）計(jì)算得到。根據(jù)式（13），對(duì)永磁體工作點(diǎn)進(jìn)計(jì)算，即可得到永磁體的虛擬矯頑力為

將式（12）、式（14）帶入到式（5）～式（11）的c和Hc中，即可分別求得徑向充磁和平行充磁下的偏心型磁極永磁電機(jī)氣隙磁密的分布。

3 定子開(kāi)槽對(duì)氣隙磁密的影響

在上文的分析中計(jì)算了等厚瓦片型磁極和偏心型磁極永磁電機(jī)的氣隙磁密分布，但沒(méi)考慮到定子開(kāi)槽對(duì)永磁電機(jī)氣隙磁密的影響。定子開(kāi)槽會(huì)在原有的氣隙磁密上疊加一系列的齒諧波，引起氣隙磁密波形部分畸變，從而產(chǎn)生一系列的凹點(diǎn)。

電機(jī)氣隙中磁力線在齒和槽下的路徑如圖8（a）所示。在忽略漏磁通的情況下，當(dāng)磁力線在齒下時(shí)，磁力線將會(huì)垂直進(jìn)入定子鐵心;當(dāng)磁力線處于槽口下面時(shí)，磁力線會(huì)有發(fā)生彎折，經(jīng)過(guò)齒側(cè)部進(jìn)入齒中，也就是說(shuō)，槽口下的磁力線其所經(jīng)歷的氣隙長(zhǎng)度要大于處于齒下的磁力線經(jīng)過(guò)的氣隙長(zhǎng)度。如果假設(shè)磁力線總是沿定子內(nèi)徑的法向進(jìn)入定子鐵心中，那么定子鐵心的數(shù)學(xué)模型如圖8（b）所示，槽口等效成一個(gè)向上的尖峰，磁力線經(jīng)過(guò)的氣隙長(zhǎng)度與槽下磁力線經(jīng)過(guò)的氣隙長(zhǎng)度相同。

在進(jìn)行等效時(shí)，假設(shè)A點(diǎn)（如圖3）為觀測(cè)點(diǎn)，則定子內(nèi)徑的近似變化規(guī)律為

其中θ0，θm，θ1分別為槽口起始位置的角度、槽中心線的角度和槽口末端位置的角度。

將a（θ）帶入到式（5）中即可求得在考慮定子開(kāi)槽的情況下，電機(jī)的氣隙磁密分布規(guī)律。

4 有限元驗(yàn)證

采用有限元算法對(duì)一臺(tái)表貼式永磁同步電機(jī)的徑向氣隙磁密進(jìn)行分析，電機(jī)參數(shù)如表1所示，經(jīng)過(guò)有限元仿真得到的磁力線圖和磁密云圖如圖9所示。

由圖10（a）可知，氣隙磁密Bg的計(jì)算值與仿真值得波形很接近，其波形誤差不大。圖10（b）分別對(duì)計(jì)算氣隙磁密波形和仿真氣隙磁密波形進(jìn)行了諧波分析，基波的誤差為1.3%，各次諧波的誤差不超過(guò)4%，驗(yàn)證了計(jì)算結(jié)果的正確性。

5 對(duì)比實(shí)驗(yàn)驗(yàn)證

采用電機(jī)對(duì)拖的實(shí)驗(yàn)方法對(duì)表1中所示的永磁同步電機(jī)樣機(jī)的氣隙磁密以及線反電勢(shì)進(jìn)行測(cè)量，并與計(jì)算結(jié)果進(jìn)行對(duì)比，實(shí)驗(yàn)如圖11所示。

將一根細(xì)導(dǎo)線從電機(jī)氣隙中穿過(guò)并且緊貼在定子鐵心內(nèi)側(cè)，電機(jī)旋轉(zhuǎn)時(shí)，導(dǎo)線將會(huì)切割磁感線而產(chǎn)生感應(yīng)電壓，感應(yīng)電壓除以鐵心長(zhǎng)度和磁場(chǎng)旋轉(zhuǎn)的線速度即為氣隙磁密。樣機(jī)經(jīng)實(shí)驗(yàn)所測(cè)的氣隙磁密結(jié)果與解析法理論計(jì)算結(jié)果的對(duì)比如圖12（a）所示，可見(jiàn)實(shí)測(cè)值與誤差值相差不大。對(duì)氣隙磁密進(jìn)行傅利葉分解，得到各次諧波分量幅值Bv，并進(jìn)行對(duì)比如圖12（b）所示。若忽略電機(jī)漏磁，氣隙磁通全部由定子齒部進(jìn)入到定子鐵心中，當(dāng)電機(jī)以角速度ω旋轉(zhuǎn)時(shí)，根據(jù)氣隙磁密各次諧波的幅值Bv可以計(jì)算出電機(jī)空載時(shí)各次諧波反電勢(shì)的波形，將諧波反電勢(shì)進(jìn)行求和得到電機(jī)空載反電勢(shì)，即

式中：fv、kwv、Φv分別為v次諧波的頻率、諧波繞組系數(shù)和磁通;N為電樞繞組每相串聯(lián)匝數(shù);lef為電樞計(jì)算長(zhǎng)度;τ為電機(jī)極距。

根據(jù)氣隙磁密分析結(jié)果算出電機(jī)的線反電勢(shì)，并和實(shí)驗(yàn)值進(jìn)行對(duì)比，如圖12（c）所示。由圖12（c）可知，計(jì)算結(jié)果與實(shí)測(cè)結(jié)果波形誤差不大。圖12（d）分別對(duì)計(jì)算反電勢(shì)和實(shí)測(cè)反電勢(shì)進(jìn)行傅利葉分解對(duì)比，基波分量誤差為4.2%，其他各次諧波分量誤差不超過(guò)9.2%，驗(yàn)證了計(jì)算方法的正確性。

為驗(yàn)證計(jì)算方法的廣泛適用性，除表1中所示結(jié)構(gòu)參數(shù)電機(jī)之外，還對(duì)另外兩臺(tái)結(jié)構(gòu)參數(shù)不相同的永磁同步電機(jī)樣機(jī)進(jìn)行的相同的實(shí)驗(yàn)測(cè)試，電機(jī)的參數(shù)如表2所示。

將樣機(jī)A與樣機(jī)B的實(shí)測(cè)結(jié)果與計(jì)算結(jié)果進(jìn)行對(duì)比，其結(jié)果如圖13所示。兩臺(tái)樣機(jī)所測(cè)得的氣隙磁密和反電勢(shì)大小與計(jì)算值相比誤差不大于5%，精度可以達(dá)到工程實(shí)際要求，證明了計(jì)算方法的廣泛適用性。

6 結(jié) 論

本文首先通過(guò)求解二維場(chǎng)中的拉普拉斯方程，建立永磁電機(jī)的數(shù)學(xué)模型，通過(guò)解析計(jì)算的方法分別計(jì)算了具有瓦片型/偏心型磁極的表貼式永磁電機(jī)中氣隙磁密，研究了電機(jī)定子開(kāi)槽時(shí)氣隙磁密的計(jì)算方法。然后將計(jì)算結(jié)果與有限元法仿真結(jié)果和三臺(tái)不同極槽配合樣機(jī)的實(shí)際測(cè)試結(jié)果分別進(jìn)行對(duì)比，其基波分量誤差不超過(guò)4.2%，各次諧波分量誤差不超過(guò)9.2%，證明了計(jì)算方法具有很高的精度和很強(qiáng)的適用性，便于設(shè)計(jì)人員在電機(jī)初步設(shè)計(jì)中對(duì)氣隙磁密進(jìn)行優(yōu)化分析以得到更好的氣隙磁密波形。對(duì)于其他形狀永磁體，諸如磁極削角，面包型磁極等，也可以采用此數(shù)學(xué)模型根據(jù)上述計(jì)算過(guò)程進(jìn)行分析計(jì)算。

參 考 文 獻(xiàn)：

[1] 李延升， 竇滿(mǎn)峰， 趙冬冬. 磁鋼充磁方式對(duì)表貼式永磁電機(jī)磁場(chǎng)影響分析[J]. 電機(jī)與控制學(xué)報(bào)， 2011， 15（12）：26.

LI Yansheng， DOU Manfeng， ZHAO Dongdong.Analytical magnetic field of magnetization manners in surface-mounted PM motor[J]. Electric Machines and Control， 2011， 15（12）：26.

[2] HAFNER Martin， FRANCK David， HAMEYER Kay.Static electromagnetic field computation by conformal mapping in permanent magnet synchronous machines[J]. IEEE Transactions on Magnetics， 2010， 46（8）：3105.

[3] ZHU Z Q， WU L J， XIA Z P. An accurate subdomain model for magnetic field computation in slotted surfacemounted permanent-magnet machines[J]. IEEE Transactions on Magnetics， 2010， 46（4）：1100.

[4] WU L J， ZHU Z Q， STATON D， etal. An improved subdomain model for predicting magnetic field of surface-mounted permanent magnet machines accounting for tooth-tips[J]. IEEE Transactions on Magnetics， 2011， 47（6）：1693.

[5] JING Libing， GAO Qixing， LIU Lin， et al. Exact analytical method for magnetic field computation and cogging torque of SPM motors[C]// 2015 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices（ASEMD）， Shanghai， China， 2015.

[6] XU Shilei， LIU Xiquan. Magnetic field computation for high-speed surface mounted permanent magnet machine with parallelly magnetized magnet segments[C]// 2017 IEEE International Electric Machines and Drives Conference （IEMDC）， Miami， FL， USA， 2017.

[7] 張炳義，賈宇琪，李凱，等.一種表貼式永磁電機(jī)磁極結(jié)構(gòu)優(yōu)化研究[J]，電機(jī)與控制學(xué)報(bào)，2014，18（5）：43.

ZHANG Bingyi， JIA Yuqi， LI Kai， et al. Study on magenetic pole structure of surface mounted PMSM [J]. Electric Machines and Control，2014，18（5）：43.

[8] 佟文明，孫靜陽(yáng)，段慶亮，等.永磁同步電動(dòng)機(jī)空載鐵耗研究[J].電機(jī)與控制學(xué)報(bào)，2017，21（05）：51.

TONG Wenming， SUN Jingyang， DUAN Qingliang， et al. No-load iron loss of permanent magnet synchronous motors[J]. Electric Machines and Control，2017，21（5）： 51.

[9] KIM U ， LIEU D K. Magnetic field calculation in permanent magnet motors with rotor eccentricity： without slotting effect[J]. IEEE Transactions on Magnetics， 1998， 34（4）：2243.

[10] RAHIDEH A ， KORAKIANITIS T. Analytical open-circuit magnetic field distribution of slotless brushless permanent-magnet machines with rotor eccentricity[J]. IEEE Transactions on Magnetics， 2011， 47（12）：4791.

[11] 孔漢，劉景林.永磁伺服電機(jī)轉(zhuǎn)子偏心對(duì)電機(jī)性能的影響研究[J].電機(jī)與控制學(xué)報(bào)，2016，20（01）：52.

KONG Han， LIU Jinglin. Study of rotor eccentricity effect on permanent magnet servo motor performance[J]. Electric Machines and Control， 2016，20（01）：52.

[12] 李琛，章躍進(jìn)，周曉燕，仇志堅(jiān).定子開(kāi)槽表貼式永磁電機(jī)轉(zhuǎn)子偏心空載氣隙磁場(chǎng)全局解析法[J].電機(jī)與控制學(xué)報(bào)，2014，18（10）：27.

LI Chen， ZHANG Yuejin， ZHOU Xiaoyan， et al. Exact analytical solution of open-circuit air-gap magnetic field for slotted surface-mounted permanent-magnet motors with rotor eccentricity[J]. Electric Machines and Control，2014，18（10）：27.

[13] LANCAROTTE M S， PENTEADO A D， PAULOS A J.Prediction of magnetic losses under sinusoidal or non-sinusoidal induction by analysis of magnetization rate[J]. IEEE Transactions on Energy Conversion， 2001，16（2）：175.

[14] 陳陽(yáng)生， 林友仰. 永磁電機(jī)氣隙磁密的分析計(jì)算[J]. 中國(guó)電機(jī)工程學(xué)報(bào)， 1994，14（5）：18.

CHEN Yangsheng， LIN Youyang. Calculation of air-gap flux density in permanent magnet machines[J]. Proceedings of the CSEE， 1994，14（5）：18.

[15] 倪有源， 崔征山. 組合磁化無(wú)槽永磁電機(jī)磁場(chǎng)分析與優(yōu)化研究[J]. 電機(jī)與控制學(xué)報(bào)， 2020， 24（3）：81.

NI Youyuan， CUI Zhengshan. Magnetic field analysis and optimization of slotless permanentmagnet machines with combined magnetization[J]， Electric Machines and Control， 2020，24（3）：81.

[16] BOULES N. Prediction of no-load flux density distribution in permanent magnet machines[J]. IEEE Transactions on Industry Applications， 1985， IA-21（3）：635.

（編輯：劉素菊）

收稿日期： 2018-12-27

基金項(xiàng)目：國(guó)家自然科學(xué)基金（51407119）

作者簡(jiǎn)介：趙國(guó)新（1979—），男，博士，研究方向?yàn)橛来烹姍C(jī)理論與設(shè)計(jì);

張 宇（1992—），男，碩士研究生，研究方向?yàn)橛来烹姍C(jī)振動(dòng)與噪聲;

葛紅巖（1989—），男，碩士，研究方向?yàn)橛来烹姍C(jī)設(shè)計(jì);

劉 勇（1985—），男，碩士，研究方向?yàn)橛来烹姍C(jī)設(shè)計(jì);

白保東（1955—），男，博士，教授，博士生導(dǎo)師，研究方向?yàn)殡姎庠O(shè)備電磁場(chǎng)分析與優(yōu)化設(shè)計(jì)。

通信作者：趙國(guó)新