基于多傳感器的數(shù)據(jù)融合算法研究

敬如雪 高玉琢

摘? 要： 文中提出基于多傳感器的數(shù)據(jù)融合算法，該融合方法先對數(shù)據(jù)進(jìn)行一致性檢驗，剔除傳感器測量的異常數(shù)據(jù)，得到最優(yōu)數(shù)據(jù)集;其次以支持度與自適應(yīng)加權(quán)估計理論為基礎(chǔ)，提高融合數(shù)據(jù)的精確度，該算法不需要提前知道任何先驗條件。實際應(yīng)用結(jié)果驗證了算法的準(zhǔn)確性，并進(jìn)行了Matlab仿真。仿真結(jié)果表明，此方法計算簡便，可以獲得比有限個傳感器的算術(shù)平均值與傳統(tǒng)的自適應(yīng)加權(quán)算法融合值更精確的估計結(jié)果，具有較高的可靠性和抗干擾性，可用于測量結(jié)果具有正態(tài)分布特性的多傳感器測量系統(tǒng)。

關(guān)鍵詞： 多傳感器; 數(shù)據(jù)融合; 數(shù)據(jù)一致性; 支持度; 自適應(yīng)加權(quán)算法; 仿真分析

中圖分類號： TN919?34? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻(xiàn)標(biāo)識碼： A? ? ? ? ? ? ? ? ? ? ? ?文章編號： 1004?373X（2020）10?0010?04

Research on data fusion algorithm based on multi?sensor

JING Ruxue， GAO Yuzhuo

（School of Information Engineering， Ningxia University， Yinchuan 750000）

Abstract： The data fusion algorithm based on multi?sensor is proposed in this paper. In this fusion method， the consistency of the data is firstly checked， and the abnormal data measured by the sensor is eliminated to obtain the optimal data set. The accuracy of the fusion data is improved based on the support degree and self?adaptive weighted estimation theory. The application of the algorithm does not need to know any prior conditions in advance. The practical application results verify the accuracy of the method， by which the Matlab simulation is carried out.? The simulation results show that the method is simple to calculate and can obtain more accurate estimation results than that of the fusion value of the arithmetic mean value of a finite number of sensors with the traditional self?adaptive weighting algorithm. It has the higher reliability and anti?interference and can be used in multi?sensor measurement systems with normal distribution characteristics.

Keywords： multi?sensor; data fusion; data consistency; support degree; self?adaptive weighting calculation; simulation analysis

0? 引? 言

物聯(lián)網(wǎng)作為自動化和智能化的融合體，它的核心是“互聯(lián)網(wǎng)+傳感網(wǎng)”， 傳感器具有低能耗、低成本、高精度和集成化的特點[1?3]，各類傳感器是傳感網(wǎng)中的必備節(jié)點。但由于傳感器本身精度和工藝靈敏度、傳輸誤差、高斯噪聲以及周圍環(huán)境對測量數(shù)據(jù)的干擾影響，在實際情況下的數(shù)據(jù)測量中，傳感器所處的位置不同，對物體同一屬性參數(shù)的測量數(shù)據(jù)有不同程度的偏差。為減少測量偏差，提高數(shù)據(jù)精度，一方面，需要提升傳感器硬件本身的測量精度;另一方面，利用算法優(yōu)化，對測量的原始數(shù)據(jù)集進(jìn)行去噪處理，可得到較高的數(shù)據(jù)融合結(jié)果，且抗干擾能力較強。陳彥如等人研究設(shè)計CMOS溫度傳感器[4]的工作溫度范圍是-125～-45 ℃，其測量精度誤差絕對值不超過1.5 ℃。本文在文獻(xiàn)[5]的基礎(chǔ)上，研究一種新的參數(shù)估計方法，此方法以自適應(yīng)加權(quán)估計理論為基礎(chǔ)，對多傳感器采集到的原始數(shù)據(jù)進(jìn)行一致性檢驗，找到數(shù)據(jù)最優(yōu)融合集;其次通過關(guān)系矩陣，找到支持度最高的傳感器，以其測量數(shù)據(jù)代替異常數(shù)據(jù)，進(jìn)行自適應(yīng)加權(quán)數(shù)據(jù)融合來估計出一個最優(yōu)參數(shù)。該算法不僅計算過程簡單，而且可以充分利用實驗中所有的測量數(shù)據(jù)，并用Matlab進(jìn)行了實例仿真。

1? 數(shù)據(jù)一致性檢驗

對多傳感器測量的原始數(shù)據(jù)進(jìn)行融合之前，利用數(shù)據(jù)探測技術(shù)中的分布圖法[6]找到并剔除異常數(shù)據(jù)[7]。分布圖中反映數(shù)據(jù)分布結(jié)構(gòu)的主要參數(shù)有：中位數(shù)TM、上分位數(shù)FU、下分位數(shù)FL和分位數(shù)離散度dF。設(shè)對物體的某一性能指標(biāo)的檢測采用N個傳感器彼此獨立地進(jìn)行參數(shù)測量，按照測量參數(shù)從小到大的順序進(jìn)行排列，得到一組檢測序列：T1，T2，…，Tn-1，Tn。其中T1是檢測序列的下限，Tn是檢測序列的上限。定義中位數(shù)TM為：

[TM=Tn2+Tn2+12]? （1）

上五分位數(shù)FU為區(qū)間[TM，Tn]的中位數(shù)，下五分位數(shù)FL為[T1，TM]的中位數(shù)。分位數(shù)離散度為：

[dF=FU-FL]? ? ?（2）

設(shè)定與中位數(shù)的距離大于[α?dF]的數(shù)據(jù)為異常數(shù)據(jù)，即無效數(shù)據(jù)的判斷區(qū)間為：

[Ti-TM>α?dF] （3）

式中：[α]為常數(shù)，一般取值為0.5，1.0，2.0等;[i]的取值為1，2，3，…，n-1，n。當(dāng)檢測序列的異常數(shù)據(jù)被找到且被剔除之后，剩下的數(shù)據(jù)構(gòu)成最優(yōu)數(shù)據(jù)集。

2? 相關(guān)支持度

在數(shù)據(jù)融合集中，數(shù)據(jù)Xi和Xj分別是第i個傳感器和第j個傳感器的檢測數(shù)據(jù)，且服從高斯分布，以其概率分布曲線Pi（x）和Pj（x）作為各傳感器的特性函數(shù)[8]，xi，xj記作Xi，Xj的一次觀測值，σi，σj為其方差，引進(jìn)置信距離測度，便于直觀反映xi與xj之間的偏差。

[dij=2xixjpi（xxi）dx] （4）

[dji=2xjxipj（xxj）dx] （5）

式中：dij為第i個傳感器與第j個傳感器所測數(shù)據(jù)之間的置信距離測度。

[pi（xxi）=12πσiexp-12x-xiσi2] （6）

[pj（xxj）=12πσjexp-12x-xjσj2] （7）

假設(shè)最優(yōu)數(shù)據(jù)集有M個數(shù)據(jù)，則由置信距離測度dij（i，j=1，2，…，m）構(gòu)成置信矩陣Dm：

[Dm=d11d12…d1md21d22…d2m????dm1dm2…dmm] （8）

給出融合上限θij，令關(guān)系系數(shù)rij的取值為：

[rij=1，? ? ?dij≤θij0，? ? dij>θij] （9）

當(dāng)rij=1，表示第i個傳感器支持第j個傳感器，反之，rij=0，則第i個傳感器不支持第j個傳感器;當(dāng)rij=1且rji=1，則表明第i個傳感器與第j個傳感器相互支持。N個具有相同精度的傳感器，在測量數(shù)據(jù)進(jìn)行數(shù)據(jù)融合后，可將參數(shù)精度提高到一個傳感器N1/2倍。通過關(guān)系矩陣Rm可找到支持度最高的傳感器，其測量的數(shù)據(jù)稱為超數(shù)據(jù)，用超數(shù)據(jù)代替被剔除的異常數(shù)據(jù)，最后進(jìn)行動態(tài)加權(quán)融合估計。關(guān)系矩陣Rm如下：

[Rm=r11r12…r1mr21r22…r2m????rm1rm2…rmm] （10）

即關(guān)系矩陣Rm的第i列之和為第i個傳感器被其他傳感器支持的支持度。傳感器支持度的計算公式為：

[si=j=1mrji，? i=1，2，…，m] （11）

3? 自適應(yīng)加權(quán)融合估計算法

自適應(yīng)加權(quán)融合估計算法的思想：基于總均方誤差最小的前提下，依據(jù)每個傳感器實時測量到的數(shù)據(jù)，動態(tài)為各傳感器分配所對應(yīng)的最優(yōu)加權(quán)因子Wi（i=1，2，…，n），其中傳感器的方差越大，對應(yīng)所分配的權(quán)值越小，以求得最終的估計值[X]貼近真實值X。假設(shè)：采用n個傳感器測量某事物的同一特性參數(shù)，σ1，σ2，…，σn是n個傳感器的方差，測量的理論值為X，每個傳感器的檢測數(shù)據(jù)為Xi（i=1，2，…，n），各檢測數(shù)據(jù)彼此相互獨立且是X的無偏估計，估計后的參數(shù)就是最終所求的融合結(jié)果。其中[X]和Wi必須滿足：

[X=i=1nWiXi] （12）

由式（12）、式（13）推導(dǎo)出總均方誤差[σ2]：

[i=1nWi=1] （13）

[σ2=Ei=1nW2i（X-Xi）2=i=1nW2iσ2i] （14）

根據(jù)多元函數(shù)求極值理論，求得在總均方誤差σ2最小的條件，各傳感器所對應(yīng)的權(quán)值為Wi（i=1，2，…，n），當(dāng)方差越小時，其對應(yīng)的權(quán)值越大。最小總均方誤差[σ2min]為：

[σ2min=1i=1n1σ2i]? ? ?（15）

其對應(yīng)的每個傳感器的加權(quán)因子[Wi]為：

[Wi=1σ2ik=1n1σ2k，? ?i=1，2，…，n]? （16）

通過式（16）對多個傳感器相應(yīng)權(quán)值Wi的計算，代入式（12），進(jìn)而可得到最終融合結(jié)果[X]。

4? 算法舉例

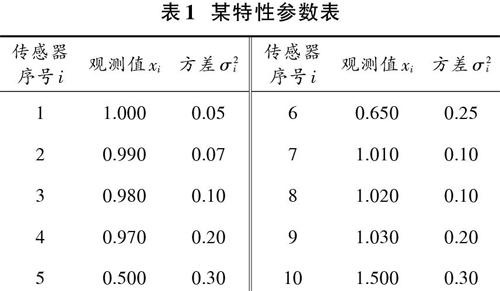
基于文獻(xiàn)[9]中的數(shù)據(jù)，采用10個同種傳感器測量物體的同一特性參數(shù)，指標(biāo)參數(shù)的實際值為1.000，測量到的原始數(shù)據(jù)如表1所示。

序號i 觀測值xi 方差[σ2i] 1 1.000 0.05 6 0.650 0.25 2 0.990 0.07 7 1.010 0.10 3 0.980 0.10 8 1.020 0.10 4 0.970 0.20 9 1.030 0.20 5 0.500 0.30 10 1.500 0.30 ]

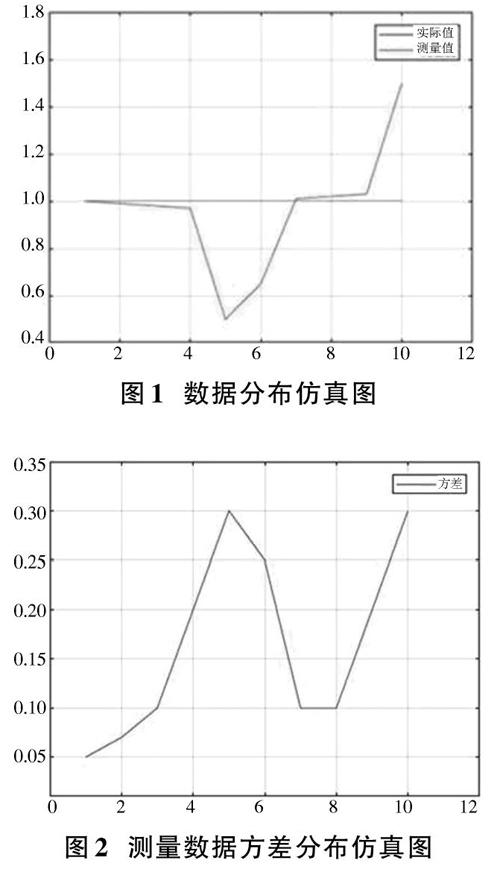
實際值與測量值的分布特征仿真圖如圖1所示，測量值對應(yīng)的方差分布仿真圖如圖2所示。

對10個傳感器同一時刻所采集到的樣本數(shù)據(jù)進(jìn)行數(shù)據(jù)一致性檢驗。先對原始數(shù)據(jù)按從小到大順序排序得到：0.500，0.650，0.970，0.980，0.990，1.000，1.010，1.020，1.030，1.500。利用式（1）求得中位數(shù)：TM=（0.990+1.000[）2]=0.995，由式（2）知，分位數(shù)的離散度dF=1.005-0.965=0.04，此次[α]取2.0，無效數(shù)據(jù)的判斷區(qū)間為[Ti-0.995]>0.08，距離大于0.08的數(shù)據(jù)為異常數(shù)據(jù)，距離越大，則表明此傳感器的數(shù)據(jù)采集準(zhǔn)確率越低;反之，傳感器的數(shù)據(jù)測量準(zhǔn)確率越高。經(jīng)過計算，5號、6號及10號傳感器的數(shù)據(jù)與中位數(shù)的偏差分別為0.495，0.395及0.505，均遠(yuǎn)大于0.08，視為異常數(shù)據(jù)進(jìn)行剔除，剩下的參數(shù)組成最優(yōu)數(shù)據(jù)集{x1，x2，x3，x4，x7，x8，x9}，假設(shè)有一變量Yi服從高斯分布，令y1=x1，y2=x2，y3=x3，y4=x4，y5=x7，y6=x8，y7=x9，數(shù)據(jù)集變成{y1，y2，y3，y4，y5，y6，y7}，且使融合上限θij=0.07，則置信矩陣D7和關(guān)系矩陣R7如下：

[D7=00.040.070.110.040.070.110.0300.030.060.060.090.120.050.0300.030.080.100.130.050.040.0200.070.090.110.030.050.080.1000.030.050.050.080.100.130.0300.030.050.070.090.110.040.020]? ? ? ? ?[R7=1100100111110011110001111000110011110001111000111]

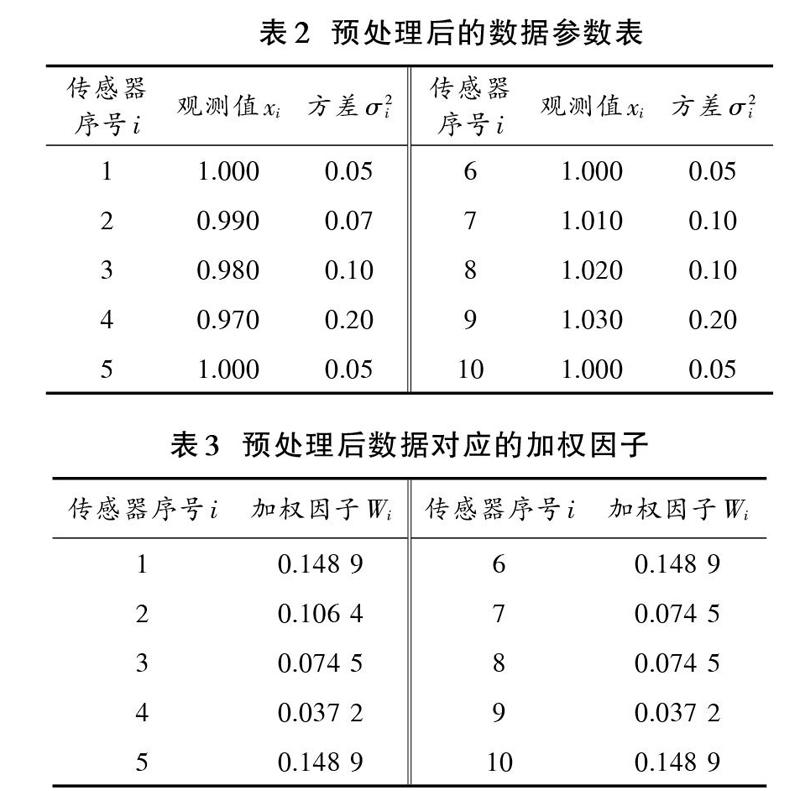
觀察矩陣[R7]得，1號傳感器的支持度為7，為支持度最高的傳感器，2號和7號傳感器的支持度同為5，支持度較次之，3，4，8，9號傳感器支持度都是3，最次之。因此用1號傳感器的超數(shù)據(jù)代替5號、6號及10號傳感器的測量值，經(jīng)過處理后的數(shù)據(jù)參數(shù)表如表2所示，依據(jù)式（16），求得預(yù)處理后各傳感器的加權(quán)因子見表3。

數(shù)據(jù)預(yù)處理后得到的方差用Matlab仿真得到圖3。

利用式（12）可計算融合參數(shù)：

[X=]1.000[×]0.148 9+0.990[×]0.106 4+0.980[×]0.074 5+0.970[×]0.037 2+1.000[×]0.148 9+1.000[×]0.148 9+1.010[×]0.074 5+1.020[×]0.074 5+1.030[×]0.037 2+1.000[×]0.148 9

=0.999 581

對于10個測量原始數(shù)據(jù)采用簡單的算術(shù)平均法：

[X=] （1.000+0.990+0.980+0.970+0.500+0.650+1.010+1.020+1.030+1.500[）10]=0.965

利用算術(shù)平均值法的計算結(jié)果是0.965，傳統(tǒng)的自適應(yīng)加權(quán)方法計算出數(shù)據(jù)融合結(jié)果是0.983 0，改進(jìn)后的自適應(yīng)加權(quán)算法結(jié)果是0.999 581。經(jīng)過數(shù)據(jù)融合對比發(fā)現(xiàn)，采用本文提出的數(shù)據(jù)融合算法估計的參數(shù)精度明顯提高，具有較高的可靠性和魯棒性。

5? 結(jié)? 語

本文提出的融合算法不需要知道任何先驗概率，且可充分使用到任何一個傳感器測量到的數(shù)據(jù)，利用數(shù)據(jù)的冗余性和互補性進(jìn)行數(shù)據(jù)融合，根據(jù)計算結(jié)果的對比，參數(shù)估計準(zhǔn)確率提高。在使用多個傳感器對事物同一屬性進(jìn)行參數(shù)測量時，針對測量到的個別異常數(shù)據(jù)，提出基于數(shù)據(jù)一致性與支持度的自適應(yīng)加權(quán)估計算法。首先，利用數(shù)據(jù)一致性對原始數(shù)據(jù)進(jìn)行預(yù)處理，剔除異常數(shù)據(jù)，尋找最優(yōu)數(shù)據(jù)集;其次，通過支持度選出測量最準(zhǔn)確數(shù)據(jù)的傳感器，用超數(shù)據(jù)代替異常數(shù)據(jù)進(jìn)行下一步的融合估計;最后，在均方差誤差最小的情況下，應(yīng)用自適應(yīng)加權(quán)算法進(jìn)行最終的參數(shù)估計。自適應(yīng)加權(quán)數(shù)據(jù)融合算法不僅可以廣泛應(yīng)用到多傳感器的溫室系統(tǒng)，而且對變速箱故障診斷與風(fēng)電軸承故障診斷[10?11]及磨礦粒度建模[12]等都有較好的改進(jìn)效果。

注：本文通訊作者為高玉琢。

參考文獻(xiàn)

[1] 方加娟，鹿艷晶，安鵬.傳感器網(wǎng)絡(luò)中的節(jié)點能耗監(jiān)測軟件設(shè)計與實現(xiàn)[J].現(xiàn)代電子技術(shù)，2017，40（12）：53?55.

[2] 黃志武，王曙霞.基于S3C2410的高精度傳感器節(jié)點嵌入式設(shè)計[J].現(xiàn)代電子技術(shù)，2017，40（19）：33?36.

[3] 張嚴(yán).基于MEMS海洋湍流傳感器實驗研究[J].現(xiàn)代電子技術(shù)，2016，39（1）：137?139.

[4] 陳彥如，陳志銘.一種大量程低誤差CMOS溫度傳感器[J].微電子學(xué)，2016，46（5）：605?607.

[5] 孫田川，劉潔瑜.基于支持度和自適應(yīng)加權(quán)的MEMS陀螺信息融合算法[J].傳感技術(shù)學(xué)報，2016，29（10）：1548?1552.

[6] 張?zhí)m勇，陸晴，耿文杰，等.基于貼近度及分布圖法的數(shù)據(jù)深度融合算法研究[J].兵器裝備工程學(xué)報，2016，37（11）：49?55.

[7] 鄭寶周，吳莉莉，李富強，等.基于異常數(shù)據(jù)預(yù)處理和自適應(yīng)估計的WSN數(shù)據(jù)融合算法[J].計算機應(yīng)用研究，2019（9）：1?8.

[8] CHEN J， HUANG N， XIONG G， et al. Adaptive weighted mean filtering algorithm based on confidence interval [J]. Journal of Nanjing University of Science & Technology， 2017， 41（3）： 307?312.

[9] 萬樹平.基于最小一乘估計的多傳感器信息融合方法[J].計算機工程，2010，36（2）：257?259.

[10] JING Luyang， WANG Taiyong， ZHAO Ming， et al. An adaptive multi?sensor data fusion method based on deep convolutional neural networks for fault diagnosis of planetary gearbox [J]. Sensors， 2017， 17（2）： 414.

[11] 李紅，孫冬梅，沈玉成.改進(jìn)加權(quán)融合算法與雙譜技術(shù)在風(fēng)電軸承故障診斷中的應(yīng)用[J].電子器件，2018，41（4）：898?904.

[12] 李德鵬，代偉，趙大勇，等.一種基于魯棒隨機向量函數(shù)鏈接網(wǎng)絡(luò)的磨礦粒度集成建模方法[J].工程科學(xué)學(xué)報，2019，41（1）：67?77.