流變基質中剛性橢球夾雜的運動演化機制

馬連華, 李雅嬈, 譚如峰

(1.河北大學質量技術監督學院，保定 071002；2.河北大學建筑工程學院，保定 071002；3.河北大學人事處，保定 071002)

彈性或黏性基體中橢球夾雜問題的研究已經有很長的歷史[1-3]。針對位于地球巖石圈中的高應變巖石流變場分配問題，中外學者采用Eshelby細觀力學方法[3-4]進行了充分的研究。Jeffery[5]首先推導了遠場均勻流動的各向同性牛頓黏性材料中嵌入剛性橢球的角速度方程。Bilby等[6]將Eshelby細觀力學理論擴展應用到橢球夾雜和宏觀區域構造具有不同黏性的流變體情況。Freeman[7]基于Jeffery的理論對各種黏性流的剛性橢球夾雜的運動進行了數值研究，并且將Eshelby方程的數值解與Jeffery方程的數值解進行了比較[8]。Je?ek[9]開發了FORTRAN程序，用來計算給定流變場中單個剛性橢球夾雜的旋轉路徑。Jiang[10-11]基于Eshelby理論并利用Mathcad計算了單個以及多個剛性和可變形橢球夾雜的演化進程。Jiang[12-13]通過引入近似算法來求解夾雜運動微分方程，提高了計算效率。向必偉等[14]從固體連續變形機制入手，重點介紹基于Eshelby理論的多尺度數值模擬思路和方法，探討流變場分配問題，揭示了嵌入基質中的橢球體內分布的流變場主要取決于橢球體與基質間的相對流變強度，橢球體的相對流變強度越低，其變形越接近于簡單剪切，且有限應變積累越快。同時還揭示，不同流變強度的橢球體內模擬拉伸線理和面理產狀的總體格局反映基質流變場特征。劉穩航等[15]介紹了韌性剪切帶中橢球狀標志體變形的最新研究進展，探討了基于Jeffery理論和Eshelby理論的數值模擬思路和方法，并利用Mathcad軟件模擬了給定條件下的橢球夾雜的運動軌跡、變形特征。Qu等[16]基于MATLAB模擬了流變巖石中橢球夾雜的運動規律，但并未考慮橢球夾雜在有限體分比下的運動演化機制。高麗敏等[17]基于Eshelby理論,通過數值模擬,將經過兩期變形疊加產生的模擬組構產狀格局與只經歷后期變形產生的模擬組構產狀格局進行對比,揭示疊加變形組構的產狀分布特征。林少澤等[18]利用適用于黏性材料的Eshelby模型，計算了橢球體內部流變場最大主應變軸和最小主應變軸方位并進行赤平投影，用以模擬線理和面理極點產狀。

1 均勻介質的連續變形機制

均勻介質的流變學在巖石流變學方面的應用開始于簡單的二維變形的研究。Jiang等[19]提出了一般的三維變形模式，推導出了速度梯度張量和位移梯度張量。

根據Jeffery[5]的定義可以得到，a1、a2、a3為橢球狀局部地質體3個應變主軸的半軸，3個半軸應滿足：a1≥a2≥a3。為了方便進行數值模擬，需要對內部和外部建立兩套不同的坐標系，其中內部的參考坐標系R′是始終與橢球夾雜的3個主軸a1、a2、a3保持平行，長度用相對應的單位基本矢量η1、η2、η3表示；而外部坐標系R使用x1、x2、x3表示，使用相對應的單位基本矢量e1、e2、e3進行表示。

剛性橢球狀夾雜在基體中的旋轉相當于其內部坐標系R′和外部坐標系R不停發生變化，同時每個旋轉位置都可以由外部坐標系R中的單位矢量ei來表示，另外也可以由內部坐標R′的單位矢量ηi來表示。在x1x2x3的坐標系統中，xi軸和x′i軸之間存在的關系為[15]

x′=Qx，x=QTx′

(1)

式(1)中：Q是從xi坐標系到xi′坐標系的過渡矩陣；QT是Q的轉置矩陣。同時，也可以定義為

e′i=Qei，ei=QTe′i

(2)

均勻介質的流動場可以使用歐拉速度梯度張量可以表示為

(3)

(4)

(5)

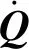
速度梯度張量L可以分解拉伸張量D和渦度張量W[18]：

L=D+W

(6)

式(6)中：

(7)

(8)

根據坐標轉換，有：

D′=QDQT

(9)

(10)

只要給定流變場的速度梯度張量L，就可以求解任一時刻流變場的運動學渦度，并可以求解經歷任意時間段的變形后的有限應變量大小、主應變大小以及應變主軸的方位。

2 等效遠場法

為了應用經典的、適用于無限大基體的Eshelby等效夾雜理論，將含橢球夾雜的代表體積單元(RVE)置于無限大的基體中并且承受遠場速度梯度L∞邊界條件，假設在遠場的邊界處施加的速度梯度張量L∞在RVE體積V內產生的流變場與直接在RVE邊界處施加的速度梯度張量L所產生的流變場是一致的，即在RVE邊界處施加L與在遠場處施加的L∞是等效的，該種方法就是等效遠場法[20]。同時，速度梯度張量L(L∞)可以分解拉伸張量D(D∞)和渦度張量W(W∞)，如圖1所示。

圖1 旋轉的等效遠場模型Fig.1 Rotational equivalent far field model

當橢球體為剛性夾雜時，僅發生剛性旋轉變形，其拉伸張量為0。

根據向必偉等[14]給出的橢球體內流變場與基體內的流變場的關系，可得到橢球夾雜的渦度張量WE為

WE=W∞-Π:S-1:D∞

(11)

式(11)中：Π為反對稱的Eshelby張量；S-1為對稱的Eshelby張量的逆；WE和W∞分別為橢球體夾雜和RVE邊界的渦度張量；D∞為RVE邊界處的拉伸張量。

根據等效遠場法，可分別建立拉伸和渦度張量與遠場拉伸與渦度張量的關系：

D=(1-f)D∞

(12)

W=(1-f)W∞+fWE

(13)

式中:f為橢球夾雜所占的體積分數。

根據上述公式，可得到：

(14)

W∞=W+f·Π:S-1:D∞

(15)

將式(13)代入式(11)，并利用式(12)，可得到：

WE=W-Π:S-1:D

(16)

由上式可以看出，橢球夾雜的渦度張量與其體分比無關。

剛性橢球夾雜的旋轉演化方程可以表示為[13]

(17)

式(17)中：Q為方位角矩陣；Θ為橢球體夾雜的角速度張量。

為提高計算效率，采用Basar等[21]給出的近似方法來求解上述微分方程：

(18)

(19)

對于可變形橢球夾雜的變形，其形狀隨著時間變化的關系式為[13]

(20)

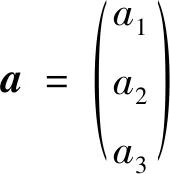
3 數值模擬

基于上述細觀力學模型，采用MATLAB數值軟件，模擬了剛性橢球夾雜的演化進程。以文獻[16]中的簡單剪切流變場中給出的參數為例，研究剛性橢球夾雜的演化進程。采用的計算數據如下。

(1)橢球夾雜的3個主半軸分別為：a1=5，a1=3，a1=1。

(2)初始方位為(100,60,30)。

(4)每個步驟的時間增量δt=0.01。

(5)模擬運行的總步數為1 000，每隔20步取一次結果。

經過計算，可以得到剛性橢球夾雜的情況。剛性橢球體夾雜的演化進程如圖2、圖3所示。

“x”是起始點，“*”是終止點圖2 單個剛體橢球夾雜Fig.2 Single rigid body ellipsoid inclusion

Step表示不同的時間步剛性橢球體夾雜的演化圖3 剛體橢球夾雜的演化進程Fig.3 Evolution of rigid body ellipsoid inclusion

4 結論

基于等效遠場法研究了黏性基體中剛性橢球夾雜的運動演化情況，得到如下結論。

(1)利用等效遠場法建立了黏性基質中剛性橢球夾雜的細觀力學理論，并基于MATLAB發展了數值計算程序。

(2)在給定速度梯度張量條件下，嵌入黏性材料的剛性橢球夾雜運動演化與體分比無關。

(3)基于發展的MATLAB程序，模擬了嵌入黏性基體中剛性橢球夾雜的運動情況，揭示了橢球夾雜的演化機制。