基于雙環路估計的鑒相器聯合跟蹤算法

韓宜靜, 曾芳玲, 汪海兵

(國防科技大學電子對抗學院，安徽 合肥 230037)

0 引言

新體制GNSS信號較傳統信號有很大改進，近期投入使用的GPS L5[1]、伽利略的E1/E5[2]及北斗二代信號[3]等均采用了BOC(binary offset carrier)調制方式和雙支路的信號樣式。但針對新體制信號，目前的跟蹤算法多是解決BOC調制的多峰值問題[4-5]，或是針對雙支路的信號體制提出的跟蹤算法[6]，并沒有文獻有效解決BOC調制與雙支路信號相結合的信號樣式的跟蹤。本文針對此問題，提出了基于雙環路估計的鑒相器聯合跟蹤算法。

1 基于BOC調制的雙支路信號體制

新體制的GNSS信號在信號結構、碼型設計及調制方式方面都有一定的改進，本文主要解決雙支路上引入BOC調制樣式的信號跟蹤問題。我們首先分別對BOC調制和雙支路上都引入BOC調制的復合信號進行介紹。

1.1 BOC調制

BOC調制是指在信號原有的BPSK調制的基礎上再調制一個二進制方波子載波，對信號進行二次擴頻，使其產生頻譜偏移。BOC調制一般記為BOC(fs,fc)或BOC(α,β)，其中，fs表示子載波頻率,且fs=α×1.023 MHz;fc表示擴頻碼速率,且fc=β×1.023 MHz，n=2α/β是調制指數。作為子載波的方波可以是正弦相位，記為BOCsin，此時Ssc(t)=sign[sin(2πfst)]，也可以是余弦相位，記為BOCcos，則Ssc(t)=sign[cos(2πfst)][7]。正弦相位BOC調制信號的歸一化功率譜密度函數為：

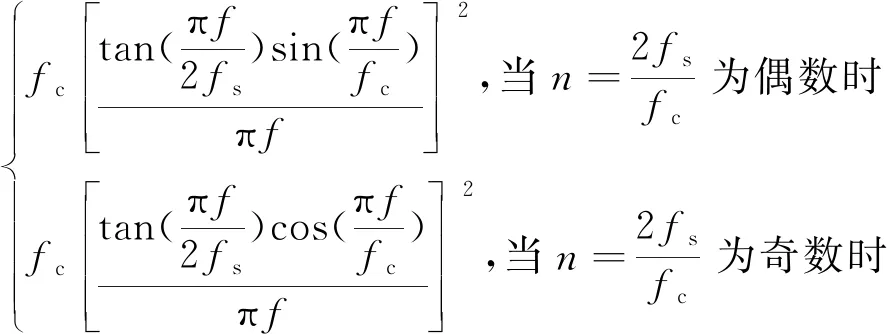
(1)

余弦相位BOC調制信號的歸一化功率譜密度函數為：

(2)

其歸一化自相關函數的表達式為：

(3)

根據式(3)可以得到PSK-R信號和BOC信號的自相關函數，如圖1所示為PSK-R(1)和BOC(1,1)、BOC(10,5)信號的自相關函數。

從BOC信號的自相關函數中可以看到，BOC調制信號的自相關函數主峰比PSK-R調制信號更陡峭，意味著BOC調制信號有著更高的定位精度，但同時BOC調制信號的自相關函數具有多個峰，各峰值出現在副載波半周期的整數倍處，調制指數越大，信號的跟蹤越容易出現誤鎖，因此，必須研究解決BOC信號多峰特性的跟蹤算法。

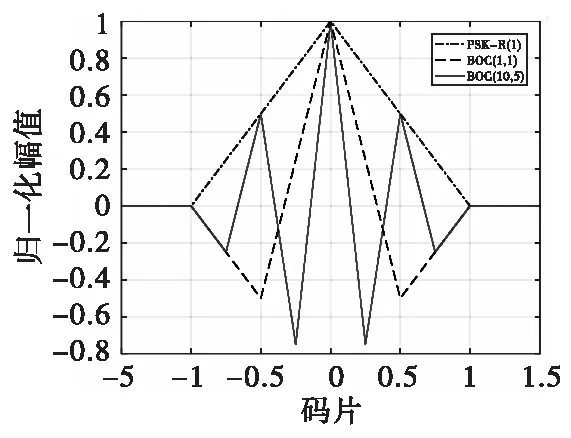
圖1 BOC信號的自相關函數Fig.1 Autocorrelation function of BOC signal

1.2 引入BOC調制的雙支路信號

雙支路復合結構是指信號調制同相和正交兩路相互正交的偽隨機碼，正交支路調制數據碼，同相支路不調制數據碼，最后通過QPSK的調制方式將信號發送出去[8]。基于BOC調制的雙支路信號體制設計框圖如圖2所示。

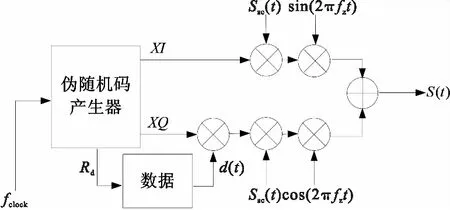
圖2 信號體制設計框架Fig.2 Signal system design framework

圖2中，fclock為偽碼產生時鐘，Rd為數據率，調制后的信號可表達為：

(4)

式(4)中，

(5)

(6)

Sp(t)、Sd(t)分別為同相、正交支路上(也叫導頻/數據支路)的信號。XI(t)、XQ(t)為同相、正交支路上的偽碼信號，采用C/A碼的產生方式，10位線性移位寄存器G2的輸出分別經過i和j個碼片的延遲，與10位線性移位寄存器G1的輸出進行模二加而產生的，則共有210+1=1 025個不同結構的偽隨機碼，將這些偽隨機碼分配給不同的接收機用作碼址，接收機接收到信號后，通過不同的偽隨機碼即可以區分信號；p是每個支路接收到的信號功率；d(t)是數據碼信號，碼率為50 bit/s，包括幀同步頭、幀編號、數據信息和校驗碼；fz是載波頻率；Ssc(t)是二進制不歸零方波子載波，子載波頻率為fs，擴頻碼速率為fc。

綜上，對基于BOC調制的雙支路信號進行跟蹤需要解決兩方面的問題：1) BOC信號的跟蹤；2) 雙支路信號的跟蹤。為此，本文首先研究對單支路BOC調制信號的跟蹤，通過對比幾種現有的跟蹤算法，選擇最優的算法并將其應用到雙支路信號體制中，以完成對信號的基帶處理。

2 基于BOC調制的單支路信號跟蹤算法

2.1 BOC調制信號跟蹤算法

目前國內外解決BOC信號跟蹤模糊問題的出發點主要分為：1) 改變自相關函數的形狀使其變為單峰值；2) 判斷跟蹤過程中是否發生了誤鎖，若發生誤鎖則需要調整本地碼相位[9]。下面介紹幾種現有的BOC信號跟蹤算法，并通過仿真對比選擇適用本信號的算法。

2.1.1BPSK-like

BOC調制信號的功率譜密度可以近似認為是兩個PSK-R信號的功率譜密度的疊加，BPSK-like法是將BOC(α,β)信號看成是兩個載波頻率相互對稱的PSK-R(β)信號，對每個主瓣都采用PSK-R(β)信號的接收方式進行處理。具體實施過程為將信號通過帶通濾波器，濾出BOC信號的兩個主瓣，分別對應為上邊帶和下邊帶，分別將上下邊帶信號的頻譜搬移到中心頻率處，再與本地偽碼進行相關[10]，其實現方案如圖3所示。

2.1.2峰跳法

“峰跳法”又稱“Bump-Jump”，是在傳統的跟蹤環路中增加超超前(very early)和超滯后(very late)兩支路，超超前、超滯后支路與即時支路之間的間隔為半個子載波周期。超前(E)和滯后(L)兩個支路的輸出構成主鑒相器，負責跟蹤碼相位及鎖定主峰，超超前和超滯后支路的相關器輸出構成輔助鑒相器，用于檢測偏離主峰的兩個副峰的幅度，通過判斷是否發生誤鎖從而對本地碼相位進行調整，確保跟蹤始終鎖定在自相關函數的主峰位置[11]。“Bump-Jump”算法的實現方案如圖4所示。

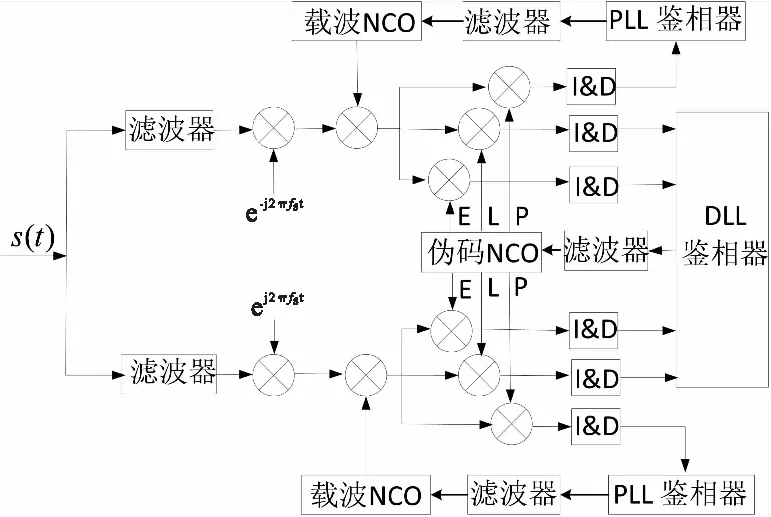
圖3 BPSK-like 跟蹤原理框圖Fig.3 BPSK-like tracking block diagram

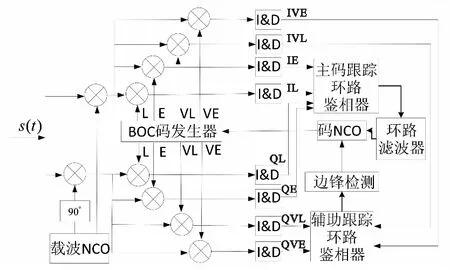
圖4 “Bump-Jump”跟蹤原理框圖Fig.4 “Bump-Jump” tracking block diagram

2.1.3自相關副峰消除技術

自相關副峰消除技術(auto-correlation side-peak cancellation technique，ASPECT)適用于BOC(n,n)類信號，利用BOC信號的自相關及BOC與偽碼的互相關之差來消除副峰的影響，實現了相關函數的重構，使得相關函數具有類似PSK-R調制信號的單峰值特性[12]，數學原理為：

(7)

式(7)中，Rsyn是修正后的自相關函數，RBOC是BOC 信號的自相關函數，RBOC-PRN是BOC信號與偽碼信號的互相關函數，λ是調整系數，其實現方案如圖5所示。

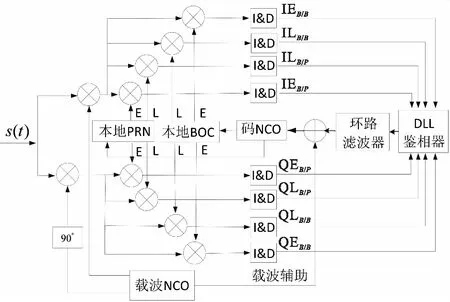
圖5 ASPECT跟蹤原理框圖Fig.5 ASPECT tracking block diagram

2.1.4雙環路估計算法

雙環路估計算法(double estimation technique，DET)將方波子載波看成是特殊形式的PN碼，分別使用子載波碼環SLL和PN碼環DLL獨立地跟蹤子載波和擴頻碼[13]，子載波碼環和擴頻碼碼環在結構上是一致的。載波環輸出同相和正交載波信號為:

(8)

子載波碼環產生超前、即時和滯后三路子載波信號分別為:

(9)

碼環產生的超前、即時和滯后三路偽隨機碼分別為：

(10)

(11)

式(11)中，round()表示四舍五入運算，Tsc為子載波周期。載波環路、子載波環路和碼環是相互獨立的，其實現方案如圖6所示。

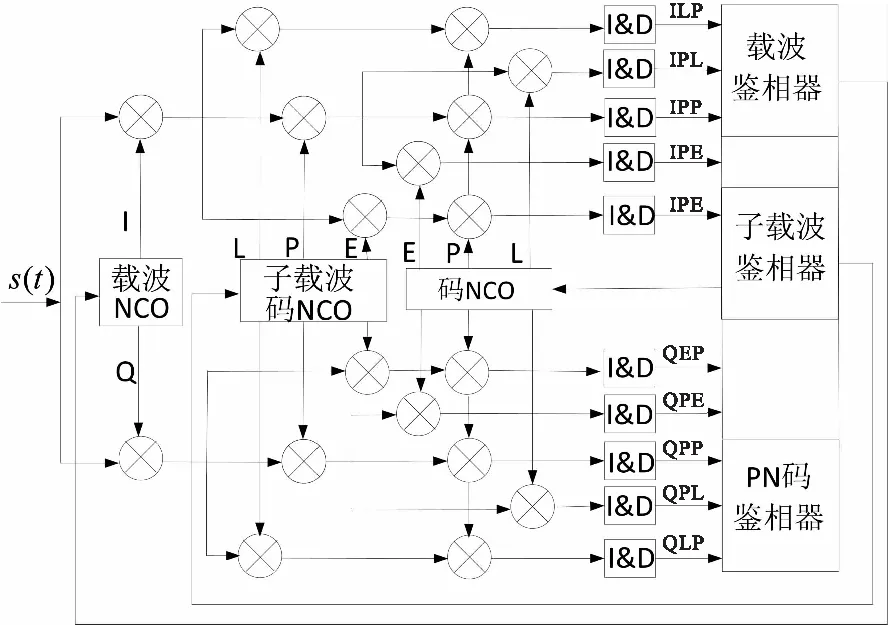
圖6 DET跟蹤原理框圖Fig.6 DET tracking block diagram

2.2 四種算法的對比分析及仿真實現

上述介紹了四種算法的跟蹤原理，本節主要對四種算法的優缺點及相應的碼跟蹤誤差進行歸納，如表1、表2所示。

表2中，BL為環路噪聲帶寬，dsc為子載波碼超前減滯后相關間距，d為碼環超前減滯后相關器間距，C/N0為接收信號的載噪比，Tcoh為預檢測積分時間，n=2α/β為調制指數，λ是ASPECT算法的調整系數，這里選λ=1。

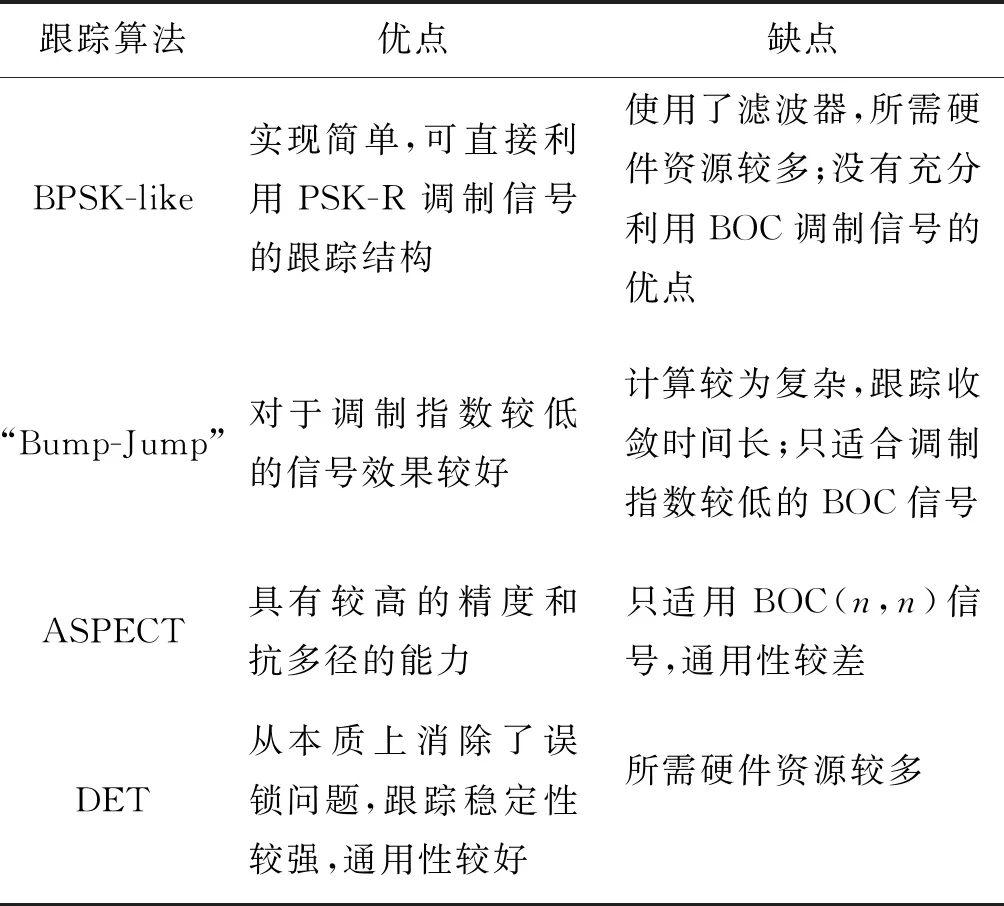
表1 四種跟蹤算法的優缺點總結

表2 四種跟蹤算法的碼跟蹤誤差

分別采用上述四種跟蹤算法對BOC(1,1)和BOC(10,5)信號進行碼跟蹤誤差的仿真，仿真得到碼跟蹤誤差隨載噪比C/N0變化示意圖如圖7所示。

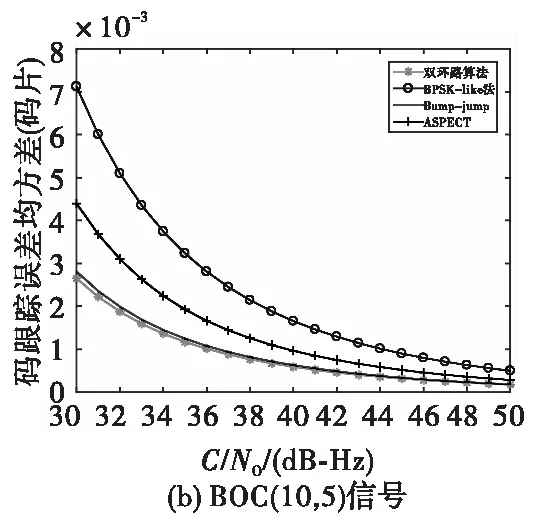
圖7 BOC(1,1)、BOC (10,5)信號的碼跟蹤誤差隨載噪比變化示意圖Fig.7 Schematic diagram of code tracking error variation of BOC(1,1) and BOC (10,5) signals with carrier-to-noise ratio

從圖7中可以看出，對于兩種BOC調制信號，四種算法的跟蹤精度從低到高均為BPSK-like、ASPECT、“Bump-Jump”以及DET算法，其中“Bump-Jump”算法的性能與DET算法的性能較為接近，綜合四種算法的優缺點考慮，最終選取DET算法為單支路信號的跟蹤算法。

3 基于BOC調制的雙支路信號跟蹤算法

3.1 鑒相器聯合跟蹤算法

鑒相器聯合跟蹤是將導頻支路和數據支路上的鑒相器輸出結果通過一定的比例系數進行線性加權[14-15]。在不考慮動態應力的前提下，碼環測量的主要誤差源是熱噪聲。對于C/A碼，當只跟蹤數據支路時，熱噪聲導致的碼相位測量誤差均方差可表示為：

(12)

式(12)中，a1為數據支路上的信號功率所占的權重。

在只跟蹤導頻支路的情況下，當預檢測積分時間取得足夠長時，由熱噪聲導致的碼相位測量誤差均方差可表示為：

(13)

式(13)中，a2為導頻支路上的信號功率所占的權重，一般a1=a2=1/2。

由于數據和導頻支路上的信號經歷了相同的碼相位延遲和多普勒頻移，使得兩個支路上的相干累加輸出在統計上是獨立的，因此可以將兩個支路上的信息結合起來對信號進行跟蹤。聯合跟蹤算法將兩個支路上的鑒相結果進行線性組合，組合后的碼環鑒相結果為[16]：

Dcomb=αdDdata+αpDpilot

(14)

式(14)中，Ddata和Dpilot分別為數據和導頻支路上的鑒別器輸出，αd、αp分別是數據鑒別器和導頻鑒別器的權重系數，組合后的線性鑒別器的碼跟蹤誤差均方差為：

(15)

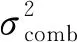
(16)

則組合后的跟蹤誤差均方差為：

(17)

3.2 基于DET的鑒相器聯合跟蹤算法

接下來將鑒相器聯合跟蹤算法與雙環路估計算法相結合。對于BOC調制信號，每個支路上都采用DET跟蹤算法。對于數據支路，碼跟蹤誤差為：

(18)

對于導頻支路，由于預檢測積分時間不用限制在20 ms以內，其碼跟蹤誤差可近似認為：

(19)

導頻支路和數據支路進行線性組合后的輸出結果為：

Dcombined=a1Ddata+a2Dpilot

(20)

融合后的跟蹤誤差為：

(21)

碼跟蹤環路的聯合跟蹤算法示意圖如圖8所示。

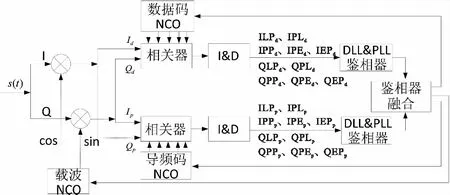
圖8 聯合跟蹤原理框圖Fig.8 Joint tracking principle block diagram

4 仿真實現

首先我們對PSK-R(1)調制信號的單數據支路跟蹤、單導頻支路跟蹤和鑒相器聯合跟蹤三種跟蹤方式進行仿真驗證。接收機帶寬設置為0.2 Hz，相關器間距設置為0.5碼片，預檢測積分時間設置為20 ms，碼環跟蹤誤差均方差隨載噪比變化示意圖如圖9所示。

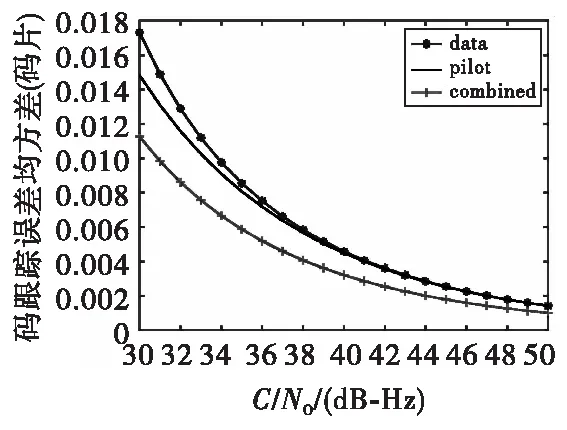
圖9 PSK-R(1)信號的碼跟蹤誤差隨載噪比變化示意圖Fig. 9 Schematic diagram of code tracking error variation of PSK-R(1) signals with carrier-to-noise ratio

從圖9中可以看出，在一定的載噪比條件下，聯合算法的碼跟蹤誤差均方差最小，然后是單獨跟蹤導頻支路，單獨跟蹤數據支路的誤差均方差最大，說明同樣的條件下單獨跟蹤導頻支路的跟蹤性能優于單獨跟蹤數據支路，而聯合算法使導頻和數據支路上鑒相器的輸出得到了充分的利用，因此具有更好的跟蹤性能。

接下來我們對基于雙環路估計的鑒相器聯合跟蹤算法的跟蹤性能進行驗證。仿真條件不變，信號采用BOC(10,5)調制樣式，仍然對比雙環路估計算法的單數據支路跟蹤、單導頻支路跟蹤及聯合跟蹤。碼跟蹤誤差均方差隨載噪比變化如圖10所示。

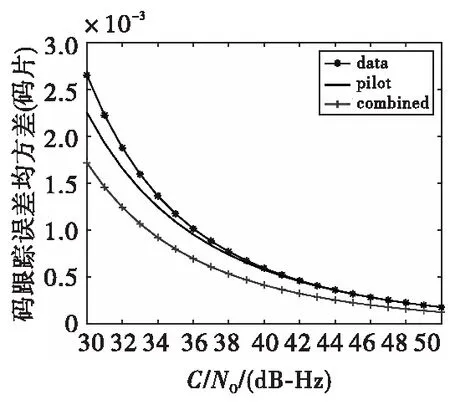
圖10 BOC(10,5)信號的碼跟蹤誤差隨載噪比變化示意圖Fig.10 Schematic diagram of code tracking error variation of BOC(10,5) signals with carrier-to-noise ratio

從圖10可以看出，基于DET的鑒相器聯合跟蹤算法可以解決BOC調制的雙支路信號的跟蹤問題，且BOC(10,5)調制信號的跟蹤精度高于PSK-R(1)信號的跟蹤精度。在載噪比達到45 dB-Hz時，使用基于雙環路估計的鑒相器聯合跟蹤算法可以使碼跟蹤精度達到0.06 m。

5 結論

本文提出了基于雙環路估計的鑒相器聯合跟蹤算法。該算法首先針對BOC信號的多峰值問題，通過對比BPSK-like、ASPECT、“Bump-Jump”以及DET算法的優缺點及碼跟蹤精度，選取最佳的BOC跟蹤算法，接著將BOC信號跟蹤算法應用到兩個支路中，對雙支路信號采取鑒相器的輸出融合方式，以完成對基于BOC調制的雙支路信號的跟蹤。仿真結果表明，不論是對BOC(1,1)還是BOC(10,5)信號，四種算法的跟蹤精度從低到高均為BPSK-like、ASPECT、“Bump-Jump”以及DET算法，因此選取DET算法應用到雙支路中。在雙支路信號跟蹤中，單獨跟蹤導頻支路的跟蹤精度高于單獨跟蹤數據支路，而聯合跟蹤的算法充分利用了接收到的信號功率，因此性能最佳。在載噪比達到45 dB -Hz時，使用該算法可以使碼跟蹤精度達到0.06 m。下一步考慮多徑環境下本文提出的跟蹤算法能達到的精度及后續解調數據的流程和誤碼率等。