地錨式懸索橋主索鞍頂推控制研究及實例分析

葉龍祥， 柯紅軍

(長沙理工大學 土木工程學院， 湖南 長沙 410114)

1 主索鞍安裝方法

地錨式懸索橋處于合理成橋狀態時，主塔只承受通過主索鞍傳遞來的兩側主纜豎向分力，兩側主纜水平分力相互平衡抵消(見圖1)，此時塔頂沒有偏位，塔底不承受彎矩。一般懸索橋的中跨遠長于邊跨，空纜時，主梁沒有吊裝，中跨側主纜減小的荷載遠大于邊跨側減小的荷載。主塔為抵消兩側主纜的水平不平衡分力，會發生順橋向偏位。如果偏位過大，可能直接導致主塔砼開裂，造成巨大經濟損失。基于以上原因，一般主索鞍在安裝時向邊跨設置一定的初始預偏量，使主索鞍兩側的水平分力相等或相差很小(一般保證主纜在鞍槽內的最大靜摩擦力大于主纜的水平不平衡分力且有一定的安全系數)，之后在主梁吊裝時再慢慢將主索鞍頂回至設計位置。主索鞍頂推方案的合理性是主塔受力安全的重要保障。

圖1 主索鞍受力示意圖

2 主索鞍頂推控制原則

主索鞍頂推控制原則有兩種：一是以主塔應力為控制原則，二是以塔頂容許偏位為控制原則。對于第一種控制原則，國內并沒有統一的規定。孫勝江等采用截面不出現拉應力且壓應力小于0.5倍軸心抗壓強度標準值，對于施工短暫狀況，可考慮將不出現拉應力的條件放寬到拉應力不大于0.7倍軸心抗拉強度標準值。王喜良采用砼截面不出現拉應力且壓應力小于抗壓設計強度，但考慮到施工臨時荷載作用是短暫的，可考慮將不出現拉應力放寬到不大于設計強度值。何為等認為橋塔截面應保持一定的壓應力，以免施工過程中因偶然荷載或突發情況導致應力減少至零甚至出現較大拉應力。第二種控制原則一般以第一種控制原則為基礎，通過試算，得出塔頂最大容許偏位。

下文算例采用的主索鞍頂推控制原則為：橋塔截面保持一定的壓應力，不能出現拉應力，壓應力小于0.5倍軸心抗壓強度標準值14.25 MPa。

3 計算方法

3.1 懸索橋施工過程

MIDAS/Civil對于施工階段的幾何非線性分析有獨立模型和累加模型。獨立模型將各施工階段形成獨立模型進行幾何非線性分析，其原理與修正后的倒拆分析法相同。累加模型是累加各施工階段的結果進行幾何非線性分析，分析時程序自動考慮構件沿初始切向激活，同時考慮時間依存特性的效果，如砼的收縮、徐變。

如圖2所示，建立兩根相連的水平梁單元，第一個施工階段激活1#梁單元，激活固結的邊界條件，激活中間節點-0.1 m強制位移荷載；第二個施工階段僅激活2#梁單元，無邊界條件與荷載。在進行施工階段分析設置時，分別勾選構件沿初始切線預偏和不勾選構件沿初始切線預偏，計算結果分別見圖3、圖4。

圖2 算例示意圖(單位：m)

圖3 沒有勾選構件沿初始切線預偏結構的變形(單位：m)

圖4 勾選構件沿初始切線預偏結構的變形(單位：m)

從圖3、圖4可看出：勾選構件沿初始切線預偏，2#梁單元會根據施工階段CS1的計算結果進行切線初始預偏，從而使2#梁單元的懸臂端在計算開始便產生0.25 m的下降；而沒有勾選構件沿初始切線預偏，2#梁單元的懸臂端則不會產生下降。

懸索橋施工過程分析的難點是主梁吊裝模擬。采用MIDAS/Civil的累加模型進行主梁吊裝分析，在模擬主梁吊裝之前進行以下設置：1) 修改主梁材料的容重為零，并給主梁單元施加梁段自重的等效梁單元荷載；2) 通過在吊桿上吊點處添加節點荷載模擬安裝吊索施工階段。以吊裝梁段S2#、N2#為例，在梁段S1#、N1#吊裝階段，先激活未吊裝梁段S2#、N2#，并將其與梁段S1#、N1#的懸臂端剛接。由于累加模型的特點，未吊裝梁段S2#、N2#會自動沿著梁段S1#、N1#的懸臂端切線預偏(見圖5)。在梁段S2#、N2#吊裝階段，先激活2#吊索單元和未吊裝梁段S3#、N3#，鈍化等效2#吊索自重的節點荷載，并給主梁S2#、N2#施加梁段自重的等效梁單元荷載，將梁段S2#與梁段S1#之間的剛接變成鉸接(見圖6)。同理完成全部主梁吊裝模擬。

圖5 吊裝梁段S1#、N1#階段

圖6 吊裝梁段S2#、N2#階段

3.2 主索鞍頂推方案確定步驟

(1) 按實際施工步驟使用累加模型模擬到空纜階段停止，釋放主索鞍與主塔接觸節點的順橋向平動約束，得出空纜僅在自重作用下主索鞍往兩側邊跨的自由滑動量，將其設置為主索鞍初始預偏量。

(2) 以主索鞍頂推控制原則為主、頂推經驗為輔(一般在主梁吊裝前期，頂推較頻繁且頂推量小)進行試算，確定主索鞍頂推時機和頂推量，以頂推次數為標準進行優化。

4 實例分析

4.1 工程概況

太洪長江大橋為主跨808 m單跨簡支鋼箱梁地錨式懸索橋，總體布置見圖7。橋梁全長1 258 m，主纜計算跨徑190 m+808 m+260 m，主跨矢跨比1/10。全橋布置66對吊索，間距12 m。全橋共劃分為68個架設梁段，分別標準梁段64個、合龍段2個、端節段2個，標準段長12 m，合龍段長9.0 m，端節段長9.2、10.8 m。按從跨中往兩側主塔的順序吊裝鋼箱主梁，梁段間預留焊縫寬度。吊裝過程中，頂板臨時連接，底板不連接，合龍后進行環縫焊接。

圖7 太洪長江大橋橋型布置(單位：m)

4.2 頂推方案

基于文獻[7]中“先梁后纜”的懸索橋成橋狀態確定方法，采用MIDAS/Civil建立橋梁有限元模型。在進行施工過程分析時，空間有限元模型很難收斂，故采用平面有限元模型(見圖8)。主纜和吊索采用只受拉單元模擬，主梁和主塔采用梁單元模擬。全橋共有564個節點、429個單元，其中180個只受拉單元、249個梁單元。邊界條件為塔底固結，兩邊主纜固結，主梁與主塔下橫梁處節點采用主從節點連接，約束豎橋向、順橋向平動。

圖8 太洪長江大橋有限元模型

按照上述方法進行主索鞍頂推方案優化試算，得出頂推時機見表1。其中1#施工階段是建造主塔，按照7 d 4 m的施工進度設置，分為48個小階段。頂推量見表2。

表1 施工階段劃分

表2 主索鞍頂推方案(以往跨中方向頂推為正)

4.3 結果分析

該橋主索鞍需進行7次頂推。施工過程中，主塔最不利應力截面出現在靠近塔底附近，以該截面為主塔控制截面。順橋向塔頂偏位(塔頂偏位以偏向中跨側為正、偏向邊跨側為負)見圖9，控制截面邊跨側和中跨側的軸向應力見圖10、圖11。

圖9 順橋向塔頂偏位

圖10 南塔控制截面應力

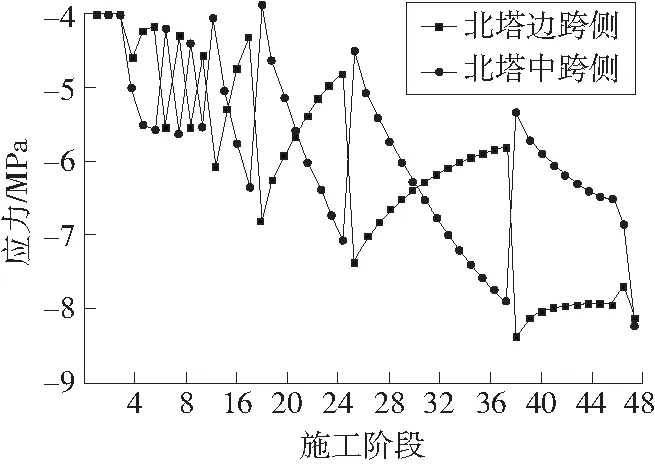
圖11 北塔控制截面應力

從圖9～11可看出：1) 在主梁吊裝過程中，主塔未出現拉應力，壓應力小于0.5倍軸心抗壓強度標準值14.25 MPa,滿足主索鞍頂推控制原則。2) 主梁吊裝前期，塔頂順橋向偏位變化較大，需頻繁頂推主索鞍。這是由于在主梁吊裝初期，主纜剛度變化較大，且主塔壓應力儲備不夠大，主索鞍需頻繁頂推來保證主塔的安全。3) 主梁吊裝過程中，塔頂順橋向偏位變化歷程均呈正負來回變化，同時主塔控制截面處中跨側和邊跨側的壓應力曲線交錯變化。這是由于隨著主梁吊裝，主塔會往中跨側傾斜，中跨側的壓應力大于邊跨側的壓應力。在主索鞍往中跨側頂推后，中跨的長度變小，邊跨的長度變大，主索鞍兩側主纜的水平不平衡分力的方向發生改變，主塔在新的主纜不平衡分力作用下往邊跨側傾斜。此時中跨側的壓應力得到釋放，中跨側的壓應力小于邊跨側的壓應力。如此循環，直至吊裝完成全部主梁。4) 地錨式懸索橋成橋時，塔頂縱橋向偏位接近于零，主塔控制截面處中跨側的壓應力和邊跨側的壓應力幾乎相等。這是由于隨著主索鞍復位，主塔承受的兩側主纜張力的水平分力平衡，主塔只承受兩側主纜張力的豎向分力。

5 結論

基于MIDAS/Civil中累加模型的特點，提出一種能連續正裝模擬主索鞍頂推的方法，該方法同時考慮時間依存特性，如砼的收縮、徐變，模擬過程更貼合實際施工步驟，計算結果更真實。將該方法應用于太洪長江大橋(單跨808 m的地錨式懸索橋)，結合主塔縱橋向偏位和主塔最不利截面軸向應力，分析主索鞍頂推的實質是通過改變各跨的長度改變主索鞍兩側主纜水平不平衡分力的方向，從而保證主塔的受力安全；成橋時塔頂縱橋向偏位接近于零，主塔中跨側與邊跨側的軸向應力幾乎相等。