基于Matlab的Gauss-Seidel迭代法電力系統潮流計算研究

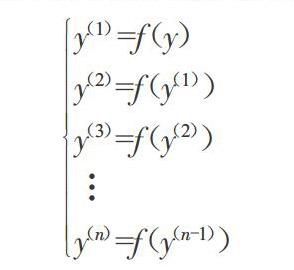
摘要：我國當前電力系統已經開始向大規模和高集成化方向發展，Matlab軟件在研究過程中可以對電力系統發揮模擬作用，但是對于電力潮流來說，需要在獲得數據以及具體節點之后，通過程序處理獲得參數。在電力系統潮流計算階段需要選用最科學的算法，由于Gauss-Seidel迭代法可以降低計算誤差，所以在提高計算精度方面發揮著重要作用。基于此，介紹了Gauss-Seidel迭代算法基本原理以及Gauss-Seidel迭代算法用于潮流計算的基本原理，進一步分析了基于Matlab的Gauss-Seidel迭代算法電力系統潮流計算方法。

關鍵詞：Matlab軟件;Gauss-Seidel迭代法;電力系統潮流計算

0 引言

在迭代法的使用過程中，無論何種處理方法都會形成一定誤差，經過多次迭代后，當采用同一數值參與計算時，則該誤差會持續增加，甚至在一定情況下產生的誤差會高于原始數值。對于本文選用的Gauss-Seidel迭代法，其優勢是能夠在形成迭代結果后，通過對該結果與下一步處理結果進行橫向對比并直接利用，從而形成精準的計算結果。

1 Gauss-Seidel迭代算法基本原理

1.1 ? ?算法使用流程

該算法的使用流程是根據數學原理得到某一參數，計算方法可以表現為y=f（x），則迭代過程可以表示為：

y（1）=f（y）y（2）=f（y（1））y（3）=f（y（2））y（n）=f（y（n-1））

將不同流程得到的外值代入到同一個計算方程，以獲得第二步結果，經過多次運算之后，每一步得到的結果都會產生一定差異。為了確定最終取得的運算參數，需要設定對比參數，計算方式為：

|y（n）-y（n-1）|≤ε

其中方程右側為計算對象在多次計算中允許的最大誤差值，需要注意的是，對于選用的算法中，函數加工廠“f（x）”中可以有多個自變量，但是因變量只能有一個，即：

y=f（x1，x2，x3，…，xn）

要根據實際的計算對象，合理確定自變量的數量和數值。

1.2 ? ?相關參數的處理

在參數處理過程中，一個參數為自變量，另一個參數為因變量，無論是何種算法都會設定一個標準值，而該標準值通常用于說明計算過程中產生的各階段的誤差程度[1]。通常情況下，該結果需要按照行業以及學科知識的要求設置，而具體計算工作由專業算法和軟件自主完成，并且只有在確定多次計算結果之后，才可以得到最精確的指標。

1.3 ? ?最終結果的獲取

事實上，在每一次迭代過程中都會產生一定的固定結果，但是不同的計算階段數據生成的實際誤差存在差異，只有在誤差能夠保持學科要求時，獲得的結果才可實際使用。另外在每一步的計算階段，都需要將產生的誤差值加入到持續性的迭代算法內，而該迭代算法在融合了誤差值后具有更高的精度，利用該方法可以使實際獲得的結果具有可靠性。

2 Gauss-Seidel迭代算法用于潮流計算的基本原理

2.1 ? ?計算參數的確定

計算參數的確定要根據電力系統的自身運行標準和研究對象確定，比如對于電力潮流來說，由于主要的評價標準是某節點中的功率和其余節點間的功率比值，尤其是對于線路的上游和下游區域，當下游的實際功率高于上游時，則會出現逆潮流現象，對電力系統造成破壞，所以無論是實際檢測，還是模擬運算，首先確定的參數是當前電力系統中的各個節點，其次通過對電壓電流的分析，確定這兩個節點的功率數值，并將獲得的參數納入計算方程中，可以在多次迭代之后和設定的標準值對比，當發現某參數經過多次迭代之后和標準值之間的誤差小于設定標準，可確定當前整個潮流系統處于穩定運行狀態。最后是實際分析，制定線路系統的優化方案。

2.2 ? ?計算公式的確定

在計算公式的建設階段，要確定潮流的變化方法和計算流程，并且將各時間點和工作步驟中產生的實際參數納入后續的計算范疇。通常情況下，由于迭代算法中計算公式不出現變化，所以可按照該方式研究最終的計算成果，讓獲得的結果可以更好地描述實際情況[2]。考慮到功率的計算方式為電壓和電流的乘積，且對電流的計算和檢測難度較小，所以主要分析當前不同節點的電流數值，此外根據不同節點的有功和無功功率數值，可獲得第2個節點的電壓以及第n個節點的電壓數值，將其納入實際的潮流計算公式內并可以得到實際的計算結果，以對平衡節點的電力參數進行討論。由于已經在計算中獲得了電壓值，將該參數直接代入潮流迭代公式中進行多次迭代計算即可。由于向某節點注入的有功功率和電壓大小已經給定，所以可以將其使用到迭代計算公式內，并對該節點的無功功率預先計算，根據功率和電流的表達式，并且加入需要考慮的電壓值參數，則可使獲得的結果得以精確計算。

2.3 ? ?計算節點的確定

在計算節點的確定過程中，由于不同的計算方法具有一定的誤差，比如某節點為發電機節點而另一節點為輸電端節點，這兩個節點的計算公式必然不同。基于Matlab的數據分析過程要求，要根據已經建成的電力系統模型確定不同的節點方式，同時將獲得的電壓參數和電流參數代入迭代算法，獲得的不同電壓值和電流值都可以納入該算法體系，以得到最終結果，并通過比較確定潮流情況。

3 基于Matlab的Gauss-Seidel迭代算法電力系統潮流計算方法

3.1 ? ?編程原理的確定

編程原理的確定階段要根據Matlab的專用編程語言，在實際研究過程確定某節點類型，分為發電機節點、配電側節點等，由于計算參數和計算方式已知，所以在編程階段可以將工作數值納入實際的編程體系中，并且按照時間變化設定相關參數。另外對于共軛電壓值，只需要做出相關處理即可，采用迭代算法可以得到節點電壓和運行相位角，在計算過程需要建立不同節點的導納矩陣，對其初始化后設定初始運行狀態值，并分析在經過一段時間以及多步驟分析后可以取得的作用效果，把獲得的電壓值輸入原有的迭代算法，同時分析在不同時間節點中該節點的實際運行參數。

3.2 ? ?軟件編程階段

軟件編程階段要容納電力學的各類參數、電力系統各節點的運行位置、不同節點電力學參數的變化方程等，通過所有數據的分析才可以將其加入實際的潮流計算階段。此外在后續的運行過程需要對相關方程和編程結果進行預處理，該過程中一方面會設定初始運行值，另一方面要研究該數值的后續運行情況，以形成實際的運行指標，當確定該指標符合對比值要求時，則可確定目前的節點潮流可以符合系統的正常運行指標。

3.3 ? ?數據導入工作

在數據導入階段，首先要設置整個供配電網絡的初始運行值，包括電壓參數、電流參數以及節點參數，并設定不同節點的電壓變化情況，按照實際運行階段的電力參數運行模式設定[2]。其次是設定專用的描述方程，包括電壓的變化方程、電流的變化方程以及實際的對比方程等，并且將實際的迭代算法與電力學的相關變化方程進行對比，當發現實際的作用階段，數據在經過了長時間運行之后，可以取得在不同運行時間點上的節點功率參數，經過橫向對比，可研究當前該參數的差值是否超出了限定標準，若發現存在這一問題時，可確定當前的作用形勢下該電力系統無法保持穩定運行狀態。最后是對電力系統的優化，以解決目前存在的潮流問題。

3.4 ? ?計算結果的獲取

在計算結果的取得和研究階段，要研究的參數包括電力輸出節點的電壓初始值、發電機節點的相位角初始值以及經過一段運行時間之后的電力參數，并讓該參數參與對比，尤其是對于發電機節點和功率輸出節點，要分析不同發電機節點的運行參數。通過該形式一方面可以研究當前發電機的發電功率是否可以符合用電指標，另一方面可研究不同的發電機節點運行過程是否會出現逆潮流問題。比如，發現上游的發電機節點功率參數為U1，下游的發電機節點功率參數是U2，其中前個數值小于后個數值，則可確定該供電系統會出現逆潮流問題。

4 結語

綜上所述，基于Matlab的迭代算法使用階段，由于迭代算法可以對不同運行過程的操作進行全方位考慮，所以在實際運行過程中，可通過當前電力系統的相關參數確定運行狀態，找到實際的運行指標。Matlab軟件經過編程之后，可以在數據優化和基礎數據獲取階段，經過多次計算得到成果，以便研究該電力系統是否存在故障以及逆潮流問題。

[參考文獻]

[1] 韋雅，文耀寬，田珂，等.基于時間序列線性大數據分析的電力系統潮流計算方法[J].機械與電子，2020，38（1）：32-35.

[2] 安軍，宋俊達，葛維春.大規模電力系統潮流計算收斂性診斷與調整方法[J].電力自動化設備，2020（2）：1-6.

收稿日期：2020-01-16

作者簡介：宋陽（1979—），男，四川樂山人，碩士研究生，高級工程師，研究方向：電力系統分析、電網穩定分析與潮流計算等。