近幾年云南省中學數學特崗教師考試試題分析與研究

盧 萍，張 露，李愛珍，施育鳳，張朝元

（大理大學數學與計算機學院，云南大理 671003）

自2012年《云南省農村義務教育階段學校教師特設崗位計劃實施方案》〔1〕頒布以來，2016—2019年這4 年，云南省特崗教師在2016 年招聘了7 200人、2017年招聘了5 000人、2018年招聘了5 409人、2019 年招聘了6 090 人，4 年共招聘了23 699 人，其特崗教師競爭比例達到了13：1，由此可見中學數學特崗教師競爭激烈。目前對特崗教師考試方面的研究主要側重于特崗教師的政策和未來的發展，且在這方面的研究上取得了一定的成果，但是對于特崗教師考試試題分析與研究的甚少。對此本文將通過收集整理2015—2018 年的云南省中學數學特崗教師考試真題，從試卷結構、考點內容、考點分值、高頻考點和試題特點等幾個方面來分析與研究。希望能夠幫助備考的考生明確試題的考查特點，有條理、有目的地備考。

1 試卷結構分析

特崗教師考試的內容主要由專業基礎知識與教育學心理學兩部分構成，本文將從專業基礎知識中的數學學科基礎知識這一模塊來對歷年考試試題進行統計分析。近幾年真題具體考查的試題題型及分值如表1所示。

從表1 中不難看出，近幾年特崗教師考試的試題題型和分值分布基本穩定，都由選擇題、填空題、簡答題3 種題型所構成，共80 分占總分120 分的66.67%。其中選擇題有10 個小題，每小題3 分，共30 分，占試卷總分的25.00%；填空題有6 個小題，每小題3分，共計18分，占試卷總分的15.00%；簡答題有5 個大題，雖然2015 年與其他三年第20、21 題所占的分值有所變動，但簡答題部分的總分都保持不變，都為32分，占試卷總分的26.67%。

表1 近幾年特崗教師考試題量分布

2 考點內容分析

根據近幾年試題的考點來看，數學學科基礎知識是特崗教師考試的重點考查對象，主要考查考生在數學領域的基礎知識。下面對各題考點做了分類整理，具體的考點分布見表2。

首先，從表2中不難看出，特崗教師考試中試題的考查范圍較廣，并且在每份真題中高中數學知識所考查的內容較多，基本上涉及了高中數學的所有知識。如：數列、向量、函數及其性質、導數、立體幾何、復數、三角函數的性質與應用、解三角形、圓錐曲線、計數原理、概率統計等。

其次，從試題的重難點上來看，試題對大學數學知識中的極限、定積分、不定積分都進行了重點的考查；對高中數學知識中的函數與導數的應用、圓錐曲線、計數原理與概率統計、立體幾何等進行了重點考查；對初中數學中的圖形與幾何、規律探索、數與代數也進行了重點考查。

最后，從試題的結構上來看選擇題（第1—10題）、填空題（第11—16題）中有些考點每年都出現，如集合運算、平面向量、三角恒等變換、極限的計算、圓錐曲線的性質、函數與導數，然而這些都是數學的基礎知識，可見特崗考試在重視能力考查的同時，也注重基礎知識的考查；對于簡答題（第17—21題）來說，明顯地可以看出來它所考查的都是綜合應用題，比如說圓錐曲線的應用、立體幾何、導數的應用、數列的應用、概率統計、不等式的應用等，這些綜合性較強的知識點，往往是特崗考試的重點和難點，這也是考驗考生掌握知識的連貫性和分析問題的綜合能力。

表2 試題數學學科基礎知識考點分布

3 考點分值分析

基于表2 中的考點分布，可將考點主要分為集合與常用邏輯用語、函數與導數、三角函數與解三角形、平面向量、立體幾何等12 個模塊。每個模塊的分值情況見表3。

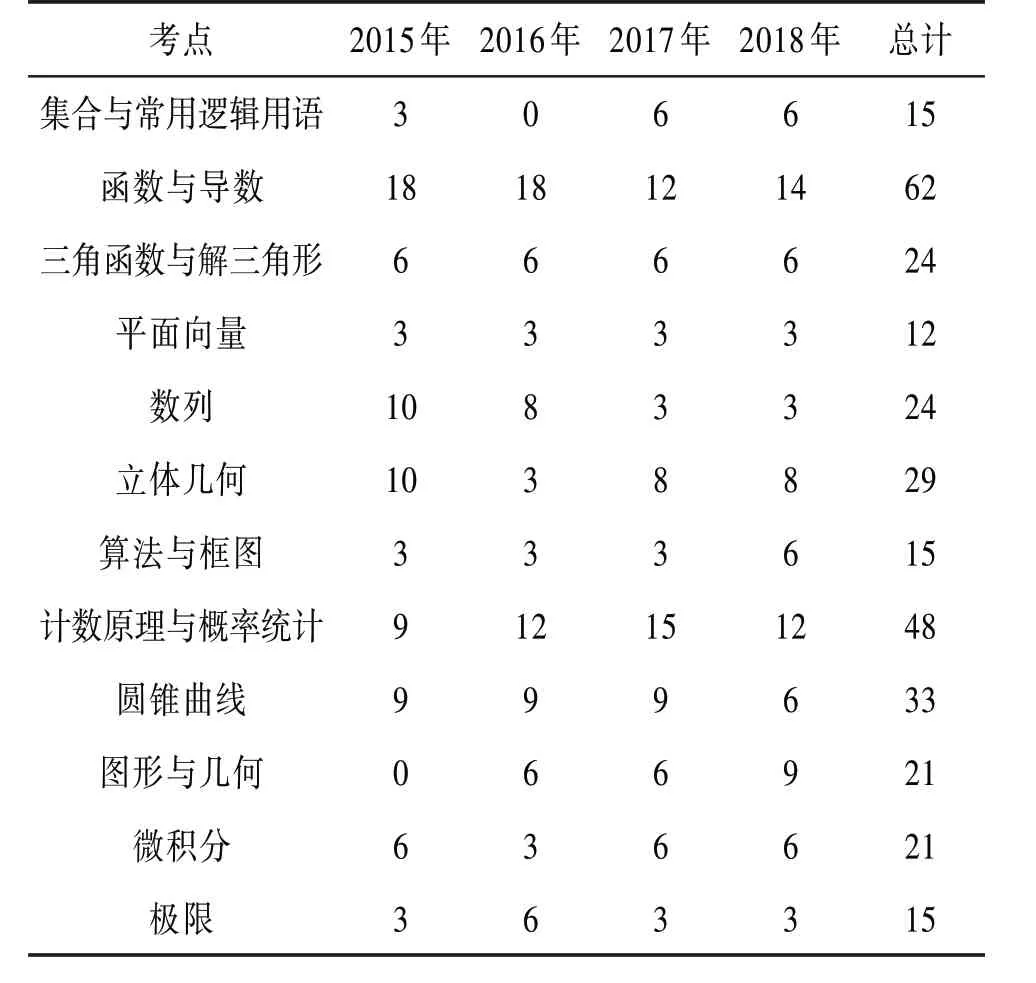
表3 試題考點分值分布

從表3試題的考點分值分布上來看，首先，可以明顯地看出函數與導數、計數原理與概率統計這兩個模塊所占的分值較高，函數與導數最高占了18分，計數原理與概率統計最高占了15分。

其次，三角函數與解三角形、平面向量在每年試題中所占的分值基本穩定，分別為6 分和3 分。而對于算法與框圖、圓錐曲線、微積分和極限這幾個考點來說它們每年所占的分值起伏不大，基本上也就相差一個選擇題或一個填空題。

4 高頻考點剖析

下面對函數與導數、圓錐曲線、立體幾何等幾個考點進行進一步的分析。

4.1 函數與導數函數是學習數學知識的一大主線，導數往往是用來鉆研函數性質的重要工具，從表3 考點分值分布中能夠看出，函數與導數在每年特崗考試中都占有舉足輕重的地位，考查時不光內容豐富，形式多樣，而且在其他的內容上也會滲透進去考查。歷年考試中函數與導數具體的考查情況見表4。

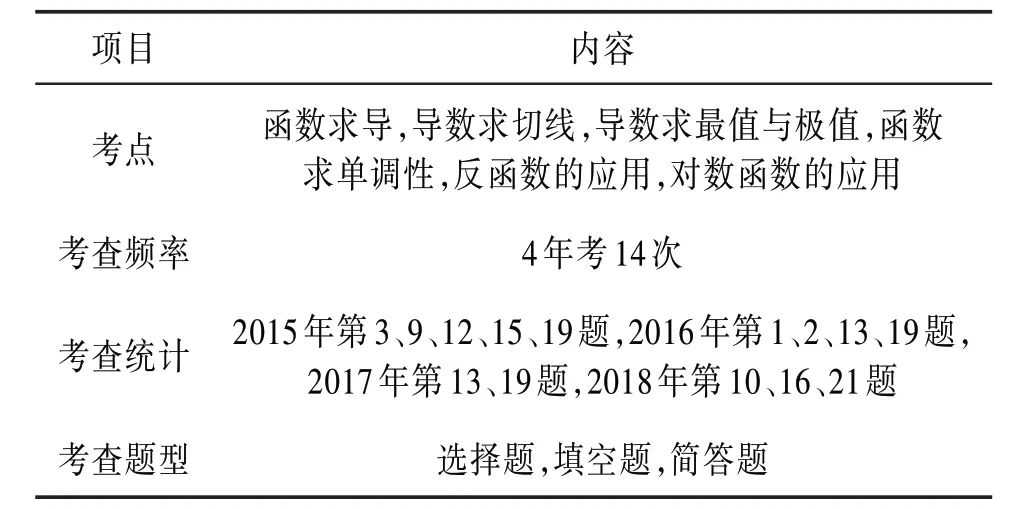
表4 試題中函數與導數考查情況

由表4的數據可以看出函數與導數是歷年特崗教師考試的重中之重，一方面，它在近幾年真題中考查頻率達到了4 年考14 次的頻率。對于這一模塊來說考查的知識范圍較廣，比如基本初等函數的性質與應用、導數的性質與應用，包括函數求導、導數求切線、導數求單調性及導數求最值與極值等幾個方面。

另一方面，可以看出考查的題型多樣，每種題型都會有所涉及。值得留意的是在近幾年的真題中，每年都有把函數與導數作為簡答題的壓軸題來考查，可見函數與導數所承載的選拔性功能尤為凸顯，考試區分度更加的明顯。現引用2018年特崗考試中函數與導數的題進行分析。

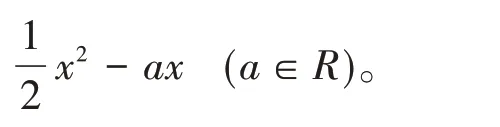
試題評析：首先，從這個題中可以明顯地看出題目采用了兩問的方式，從易到難，區分度較為明顯。且它是一道綜合性較強的試題，將函數求導、導數求單調性、極值、最值等幾個方面緊密地聯系在一起。

其次，第一問它所考查的是求函數的極值，這是一個常規的解法，只要求出函數的導數和函數的單調性，根據函數的單調性求出極值即可。而第二問考查的是含參求最值，做這個問時需要用到二次求導，這也很好地考查了考生的數學思維能力和計算能力，為選拔優秀人才提供了載體。

4.2 圓錐曲線圓錐曲線是解析幾何中的核心內容，同時也是特崗考試中的重點考查對象，主要的內容有曲線與方程（圓、橢圓、雙曲線、拋物線的方程）、圓錐曲線與直線的位置關系和圓錐曲線的綜合應用。具體的考查情況見表5。

表5 試題中圓錐曲線考查情況

從表5 中可以看出，除2018 年外考查的題型都為一個選擇題和一個簡答題。其中選擇題所考查的都是圓錐曲線的性質，簡答題考查的是圓錐曲線的應用，難度較大，所以考生對圓錐曲線的理解不能只停留在表面，要看到知識的本質，不然在做簡答題時，就會沒有思路，找不到突破口。比如說下面兩題：

例2 （2015 年第5 題〔3〕）已知雙曲線的中心在原點，焦點在y軸上，一條漸近線的方程為x-2y=0，則它的離心率為（ ）。

試題評析：從例2中可以看出，它所考查的是雙曲線性質中的漸近線方程和離心率。這個題比較基礎，只要了解雙曲線的性質且會靈活地運用即可。

從例3 中可以看出，它所要考查的是橢圓上動點到定點距離的最大值，我們知道幾何中的最值問題通常都是可以轉化為函數問題來求解，因此本題中的動點到定點間的距離問題就可以構造出關于y的一個函數，通過求這個函數的值域就可以得到它的最值，這種利用函數法求最值的方法也是較為普遍的一種方法。

4.3 立體幾何立體幾何是特崗考試的熱門考點，它主要考查考生的空間想象能力和邏輯思維能力。通過對近幾年的真題統計分析不難看出，立體幾何在每年的特崗考試中都會出現。具體的考查情況見表6。

表6 試題中立體幾何考查情況

由表6可以看出立體幾何在試卷中主要以簡答題形式出現，其次是以填空題的形式來考查。從考點上來看，它所考查的知識點與高考試題中考查的知識點基本上是一致的，比如說下面的這兩個真題：

例4 （2018 年第20 題〔4〕）如圖1，所示的五面體ABCDEF 中，四邊形ABCD 為梯形，且∠DAB=60°，EA=ED=AB=2EF=2，EF∕∕AB，M 為BC的中點。求證：FM∕∕BDE。

圖1 題圖

例5 （2017 年第21 題〔5〕）如圖2，在直三棱柱ABC-A1B1C1中AB=1，AC=AA1=，∠ABC=60°。

（1）求證：AB ⊥A1C1；（2）求二面角A-A1C-B 的大小。

圖2 題圖

試題評析：立體幾何證明主要是解決兩類問題：一是證明平行垂直類問題，其中主要是證明線與線平行垂直、線與面平行垂直和面與面平行垂直，然而解決這一類問題通常采用它們的判定定理來求解。如例4 與例5 第一問；二是求解夾角問題，主要是求解異面直線所成的角、直線與平面所成的角和二面角，解決這類的問題主要是采用綜合法和向量法來求解。綜合法主要是考驗考生的空間想象能力和邏輯思維能力，使用綜合法來求解的關鍵是找到它們所成的角即可。向量法主要是考查考生數形結合的思想，將幾何問題轉化為代數問題，而使用向量法來求解的關鍵是建立空間直角坐標系、找出點的坐標和掌握向量的基本運算。無論是采用綜合法還是向量法來求解，都是將角的問題轉化為線線角來求解，考生可以根據自己的特長選擇適當的方法來求解。

5 試題特點分析

5.1 層次分明根據近幾年試題的考點來看，數學學科知識是特崗教師考試的重要考查點，主要考查考生在數學領域的基礎知識。把數學學科基礎知識分為初中、高中、大學3 個階段，分析各階段分值分布，見表7。

表7 各階段分值分布表

從表7 中不難看出高中數學知識在數學學科基礎知識中占主導地位，高達79.38%，初中、大學兩部分的知識所占比例都相對較少也比較均衡，其中初中知識部分占比為9.37%，大學知識部分占比為11.25%。因此在備考時，可將著眼點放在高中的知識上。

5.2 綜合性強從近幾年的真題上來看，由于每份試題的容量有所限制，每一個知識點不可能都設計一個題來考查，所以真題基本上呈現的都是綜合性的試題，將多個知識點緊密地聯系在一起，主要來考查考生的綜合分析能力、理解能力及邏輯思維能力等，比如說上面提到的例1，它考查導數時將多個導數的性質融匯在一起。不光考查了考生對基礎知識的掌握能力，更主要的是考查考生的綜合分析應用能力和靈活性，若平時習慣于死記硬背或是機械地進行模仿，不能靈活地應用，要正確且迅速地解決綜合性強的題，是很困難的一件事。

5.3 基礎性實在歷年的特崗試題中有100 分的數學知識與20 分的教育知識，其數學知識占比有83.33%，數學基礎知識占比66.67%。因此在備考過程中夯實數學基礎是保證高分的關鍵，在掌握基礎知識的過程中要注意數學基礎知識和基本技能是形成和發展數學能力素養的必要基礎，是領悟數學基本思想的重要載體，特崗考試對基礎知識的考查不是對知識的機械記憶和簡單模仿，而是側重于考查考生對基本概念的理解及基本思想方法的應用〔5〕，其基礎性實的屬性也決定了備考過程中加快基礎框架的構建是十分必要的。

5.4 理論聯系實際縱觀近幾年的特崗真題，在某些題目的設計上重視聯系生活實際，注意創設情境，在解決情境問題時，注重考查考生的信息處理能力〔6-7〕。如例6、7。

例6 （2017年第16題〔5〕）某公司一個月生產產品1 890 件，其中特級品540 件，一級品1 350 件，為了檢驗產品的包裝質量，用分層抽樣的方法，從產品中抽取一個容量為70的樣本進行測試，其中抽取的特級品的件數是。

例7 （2018年第19題〔4〕）某校倡導為貧困生募捐，要求在自動購水機處買一瓶礦泉水，便自覺向捐款箱中至少投入一元錢。現統計了連續5 d 的售出礦泉水箱數和所得捐款額情況，如表8：

表8 題表

學校計劃將捐款以獎學金的形式獎勵給品學兼優的特困生，規定：特困生綜合考核前20名，獲一等獎學金500 元；綜合考核在21～50 名，獲二等獎學金300元；綜合考核在50名以后的，不得獎學金。

（1）若x 與y 成線性相關，則某天售出9 箱水時，預計所得捐款額為多少元?

（2）假設甲、乙、丙三名學生均獲獎，且各自獲一等獎和二等獎的可能性相同，求三人獲得獎學金之和不超過1 000元的概率。

數學來源于生活，同時也必將應用于生活，學數學就是為了解決生活中所遇到的問題。以上兩個題都是來自于日常生活中的案例，運用數學知識去分析和處理生活中的數據，進一步地考查了考生對知識點的理解和應用。

6 結論

本文通過收集整理2015—2018 年云南中學數學特崗教師考試真題，從試卷結構、考點內容、考點分值、高頻考點和試題特點等幾個方面進行了分析與研究，得到了如下結論：

首先，從中學數學特崗教師試卷的結構上來看，歷年數學學科基礎知識這一模塊的試卷結構均由選擇題、填空題、簡答題三部分構成，共80 分，占試卷總分的2∕3，可見數學學科基礎知識是拉開各考生的差距所在。因此在備考過程中累積數學學科基礎知識是重要的。

其次，從試題的特點上來看，歷年的數學學科基礎知識中高中所占的比例都遠遠大于初中，高中的數學知識占比達79.38%，所以高中的數學知識更要牢牢把握，尤其是想在短時間內備考特崗教師的考生，重點復習高中數學知識，以此為基礎開拓知識面，是快速備考特崗教師的關鍵。

最后，值得注意的就是，在各考點中函數與導數、圓錐曲線、立體幾何、計數原理與概率統計這4類題型的總占比達到了35.83%，因此在備考過程中，這4類題型是值得研究和深入學習的，這樣在考場上遇到這類高頻率、高分值的題目，能夠高效地作答也是為其他難題、新題爭取更多突破的時間。