總體最小二乘回歸模型中回歸參數的一種新估計算法

曹邦興

（廣州大學松田學院，廣州 511370）

在測量數據處理中，由于采樣誤差、建模誤差等系數矩陣偏差普遍存在，此時普通最小二乘法（ordinary least squares，LS）得到的參數估計值不再是最優無偏估計，總體最小二乘法（total least squares，TLS）得到的回歸方程更加合理可信〔1-3〕。對于總體最小二乘法回歸參數的估計，目前普遍采用的方法是奇異值分解和Euler-Lagrange 逼近，但這兩種算法的推導要涉及Eckart-Young-Mirsky 矩陣逼近理論等，復雜難懂，令許多學習者難以接受，也使其應用受到了限制〔4-8〕。本文引入回歸參數的一種新迭代算法，闡述了其理論依據、推導過程、算法實現步驟，最后通過實際算例對得到的線性回歸方程進行顯著性檢驗。

1 一元線性回歸分析

1.1 一元線性回歸最小二乘法概述自然科學與社會經濟等現實問題中，兩個變量之間的相互關系可以大致分為兩類：一類是一個變量的變化能完全決定另一個變量的變化，如物理學中電壓U 與電流I 之間存在的確定性函數關系U=R ?I（R 表示電阻）；另一類是非確定性關系，如農作物產量與施肥量之間存在密切的相關關系，但這種相關關系并無確定性的函數值對應關系。回歸分析方法就是處理變量之間相關關系的一種有力工具。

設x 是一個可以精確觀測的普通變量（即不含觀測誤差），y 是與x 有相關關系的隨機變量（因變量），研究y 與x 之間相互關系的統計方法稱為一元線性回歸分析。

假設y與x之間存在近似于y=β0+β1x 這樣的線性關系，可以依據殘差平方和

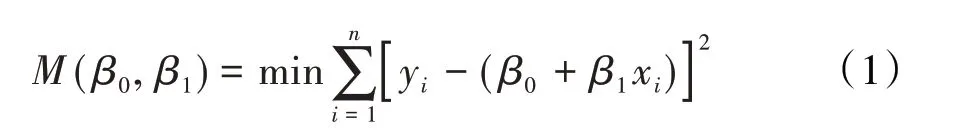
根據微積分極值原理，令

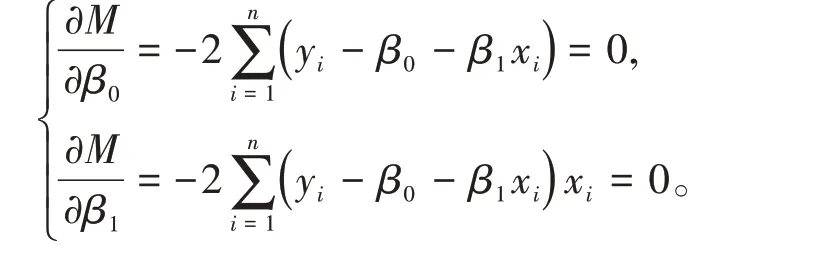
整理后得正規方程組

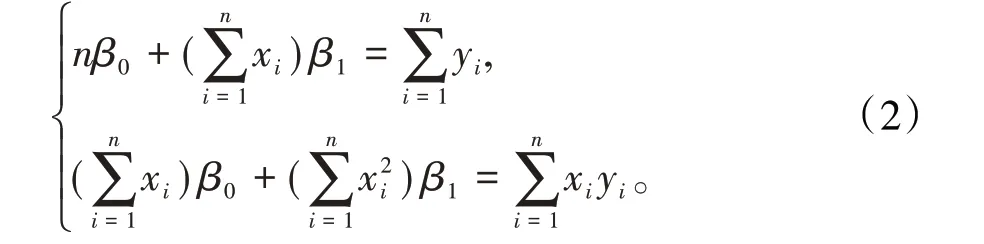
解此正規方程組得β0、β1的最小二乘法估計為

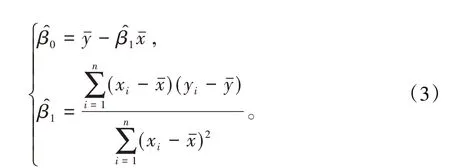
1.2 總體最小二乘法估計當需要同時考慮自變量的觀測誤差η 和因變量的觀測誤差ξ 時，平差模型（1）式也應該改為〔1，3〕

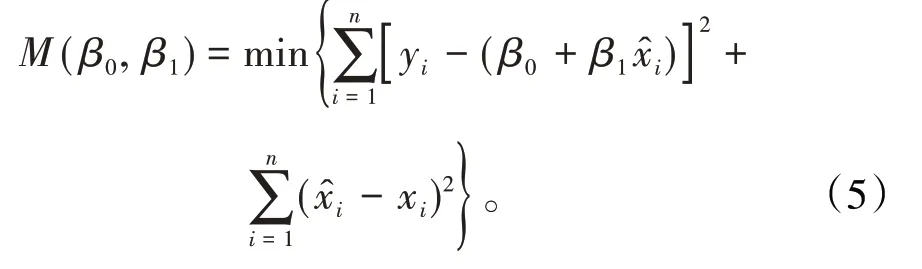
式中等式右邊的第一項代表各組數據關于因變量的觀測誤差ξ 的平方和，第二項代表自變量的觀測誤差η的平方和。總體最小二乘法就是要尋求回歸參數β0、β1的值，使（5）式達到最小。

將（5）式分別對x?i求偏導數并由極值原理，令偏導數為零，整理得

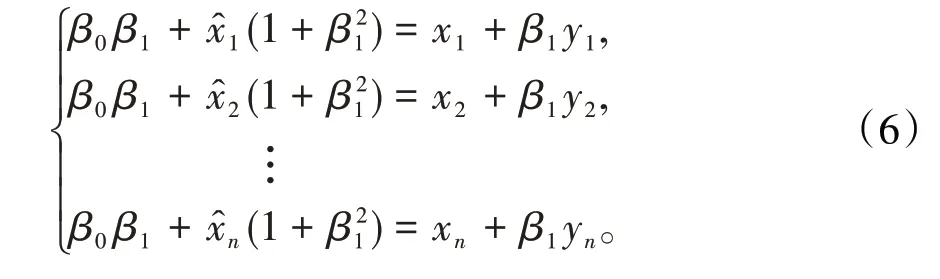
這一部分用于改正自變量觀測誤差對回歸參數β0、β1的影響。

將（5）式分別對β0、β1求偏導數并由極值原理，得

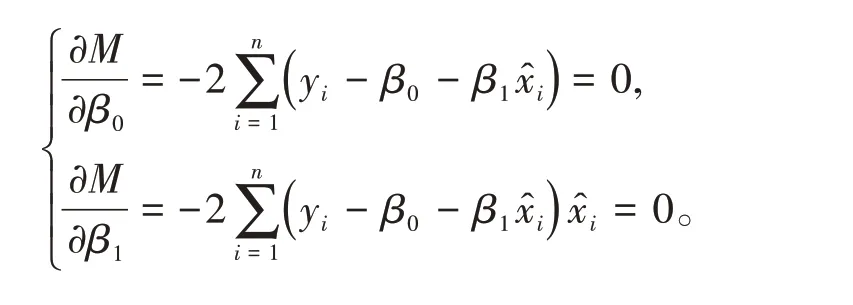
得正規方程組

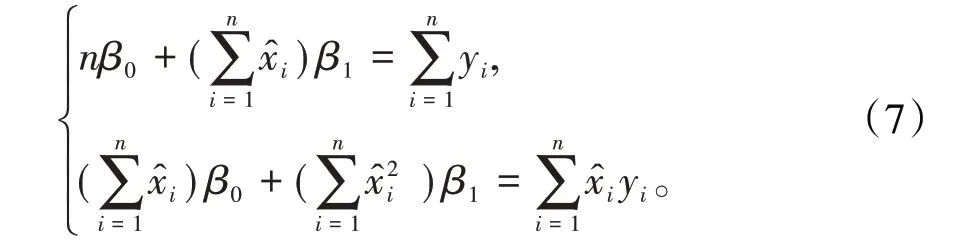
對比正規方程組（7）和正規方程組（2），其差別就是（7）式中用x?i替換了（2）式中的xi，用于修正自變量的觀測誤差。

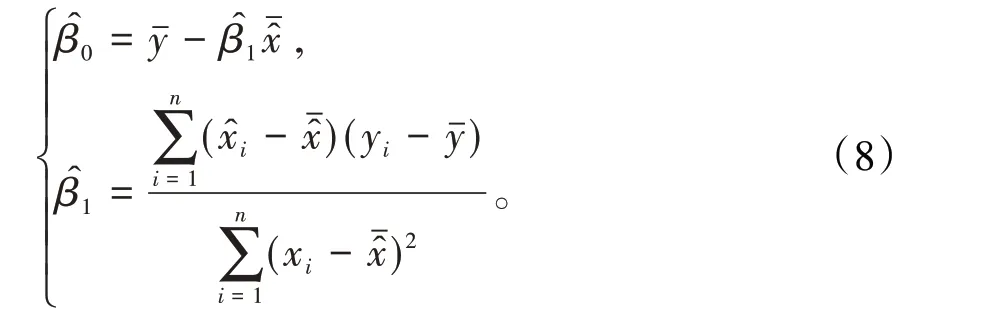
基于上述推導過程，回歸參數β0、β1的迭代計算步驟可歸納如下：

第一步：由已知的n 組觀測數據，用普通最小二乘法（3）式計算出初始值

第四步：重復第二步、第三步，直到前后兩次回歸參數之差的平方和小于事先設定的限值，或事先設定的循環次數已經完成，則停止迭代計算，并由最后一次得到的值寫出回歸方程；

第五步：進行顯著性檢驗。

2 多元總體最小二乘線性回歸分析

將前面的一元線性回歸推導過程進行擴展，可得到多元線性回歸分析。

2.1 普通多元最小二乘法估計設隨機變量y與m個一般變量x1,x2,…,xm的線性回歸模型為y=β0+β1x1+β2x2+…+βmxm，樣本有n 組觀測數據(xi1,xi2,…,xim;yi)(i=1,2,…,n)，則上述線性回歸模型可以表示為

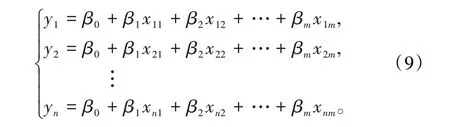
為計算方便，引入3個矩陣X、Y、β分別為

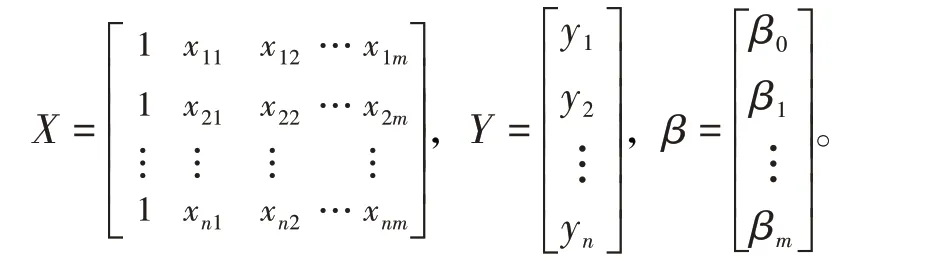
（9）式可以表示成矩陣形式Y=X ?β。

n元線性回歸方程的平差模型為

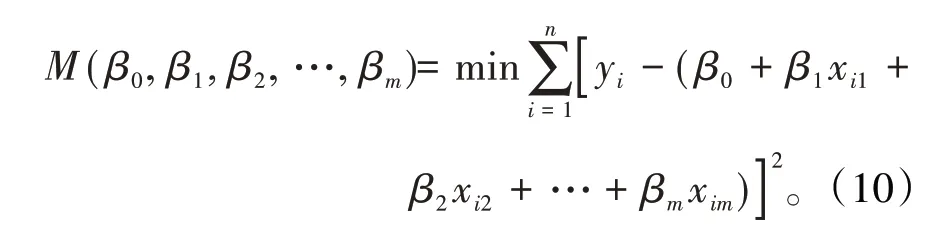
將（10）式分別對β0,β1,β2,…,βm求偏導數并由極值原理，令偏導數為零，經整理后，得到下面矩陣形式的n元正規方程組

解此方程組得回歸參數的估計值矩陣為

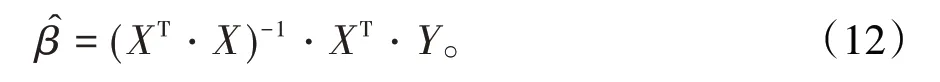
2.2 多元總體最小二乘法估計當需要同時考慮自變量的觀測誤差η 和因變量的觀測誤差ξ 時，回歸方程應表示為

矩陣X、Y、β 如前面所述，此處增加了兩個隨機誤差矩陣

分別表示自變量系數矩陣X 的觀測誤差和因變量Y的觀測誤差。

將（13）式改寫成

設矩陣A=[ X,Y ]表示增廣矩陣，B=[ η,ξ ]表示誤差矩陣，多元總體最小二乘法TLS 可以表示為約束最優化問題

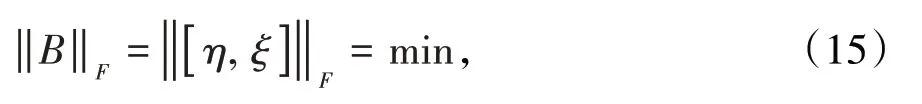
式中‖ · ‖表示Frobenius范數。

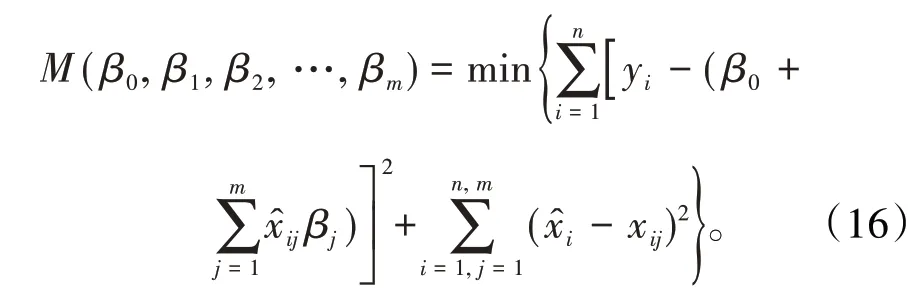
多元總體最小二乘法TLS 的平差模型也應該改為〔9-10〕基于總體最小二乘法的參數估計，就是要尋求回歸參數β0、βj(j=1,2,…,m)的值，使（16）式能夠達到最小。

將（16）式分別對x?ij求偏導數并由極值原理，令偏導數為零，經整理后，得到

再將（16）式分別對β0、βj(j=1,2,…,m)求偏導數并令導數等于零，整理得

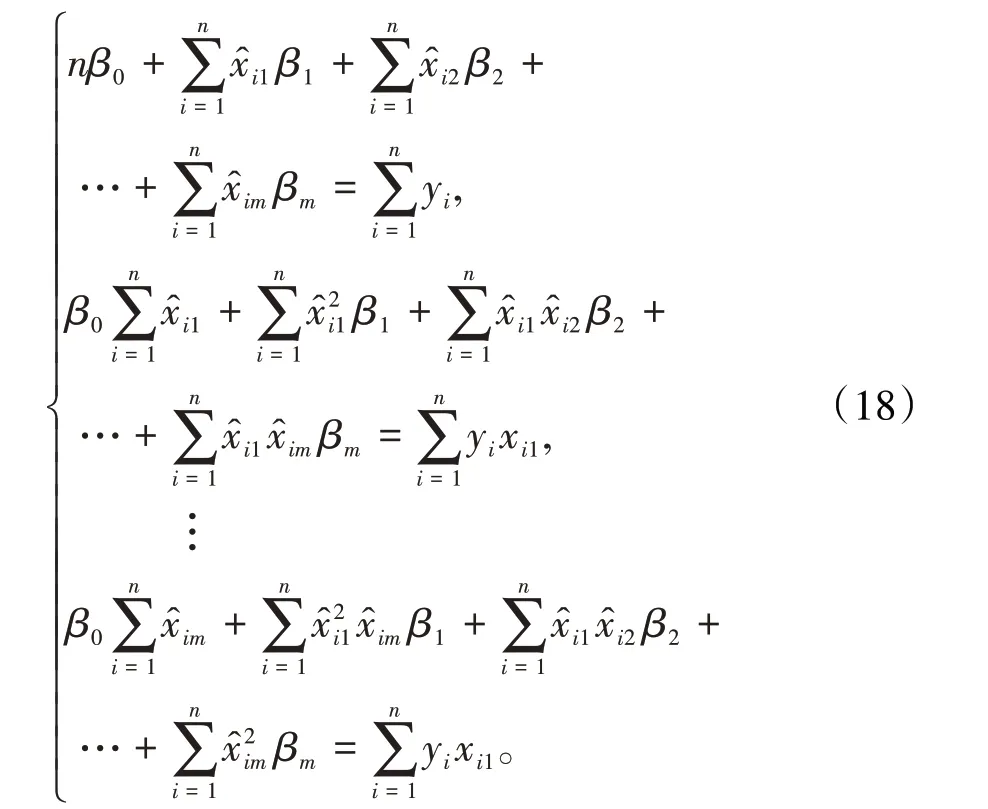
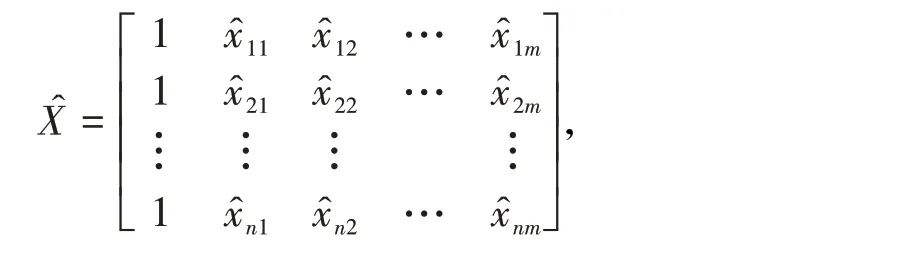
這一部分代表了因變量誤差矩陣ξ 對參數矩陣β 的影響。設矩陣仿照“2.1”中的（11）式和（12）式，可解得回歸參數β矩陣為

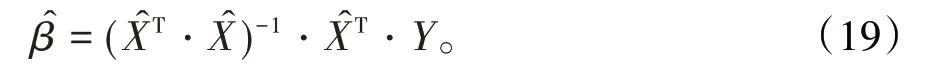
最后，基于迭代法的總體最小二乘法回歸參數矩陣β的計算可歸納如下：

第四步：重復第二步、第三步，直到前后兩次回歸參數之差的平方和小于事先設定的限值，或事先設定的循環次數已經完成，則停止迭代計算，并由最后一次得到的值寫出回歸方程；

第五步：進行顯著性檢驗。

3 實例分析

為驗證本文算法的有效性和可靠性，用Matlab 2017b 軟件進行了大量模擬測試，下面是其中的一個總體最小二乘法五元線性回歸算例。

3.1 測試數據觀測數據值見表1。表1 中的部分數據引自文獻〔11〕。

作為對比，首先采用奇異值分解法（SVD 法）來進行回歸參數估計，在Matlab 2017b 上最終算得右奇異向量矩陣的最后一列列向量為

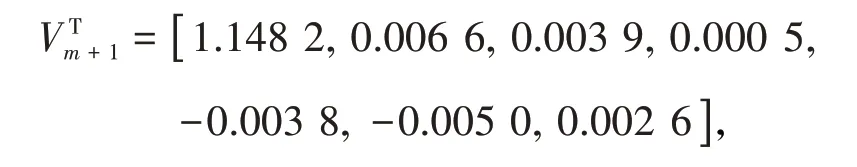
回歸參數矩陣β為

即五元線性回歸方程為

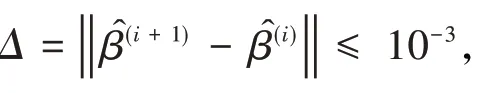
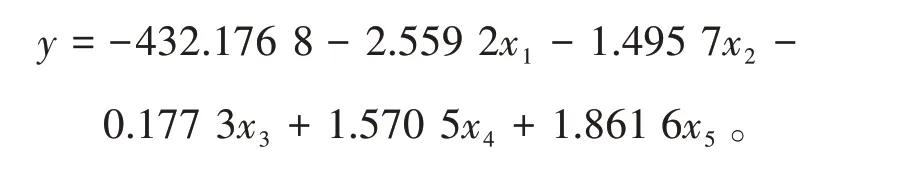
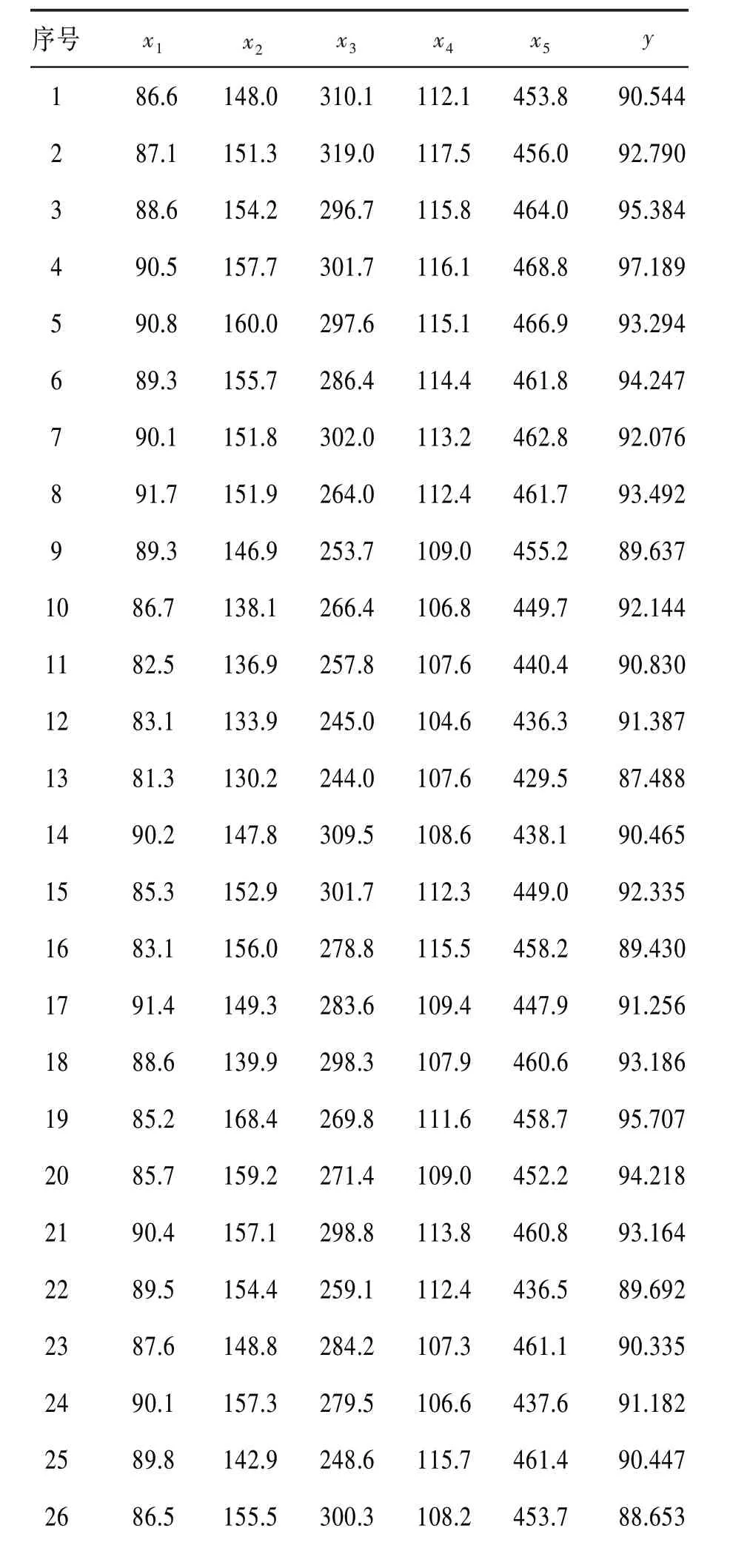
表1 觀測數據值

3.2 顯著性檢驗對線性回歸方程顯著性檢驗的重要方法之一是進行F 檢驗，其方法是根據平方和分解式，直接檢驗回歸方程對樣本數據的擬合程度。平方和分解式如下：

（1）總離差平方和SST

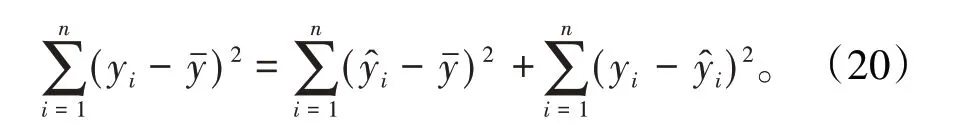
總離差平方和反映觀測值yi(i=1,2,…,n)的離散程度，也即反映因變量的總波動程度。

（2）回歸平方和SSR

（3）殘差平方和SSE

此外，如果因變量與自變量之間存在高度的線性相關關系，則回歸方程的擬合精度就越高，擬合優度就越好，其判斷數據就是樣本決定系數R2。

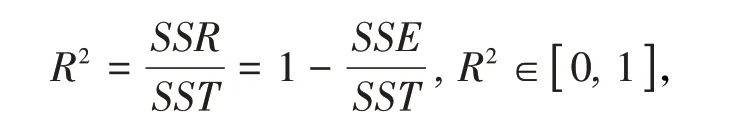
從（20）式可以看出，總離差平方和SST 是由回歸平方和SSR、殘差平方和SSE 這兩部分組成，其中回歸平方和SSR反映由于自變量的變化而引起因變量的線性變化程度，殘差平方和SSE 是由隨機因素造成、不能由自變量解釋的波動，所以SSR 占SST 的比例越大，即樣本決定系數R2越接近于1，則表明線性回歸方程的擬合效果就越好〔12〕。

樣本決定系數R2的具體計算公式是

兩種算法的離差及樣本決定系數見表2。從表2可以看出：

（1）兩種算法的總離差平方和SST分別為746.581、735.166，比較接近。

（2）兩種算法的樣本決定系數R2分別為0.879、0.912，本文算法的樣本決定系數R2更接近于1，即得到的估計值與樣本觀測值更加接近，本文算法具有更好的擬合效果。

（3）兩種算法的樣本決定系數R2分別為0.879、0.912，其統計學含義是：因變量變化的87.9%、91.2%都可以用自變量的變化來解釋，表明這兩種算法的回歸模型都具有良好的解釋能力，但本文算法的解釋能力更強，具有相對優勢。

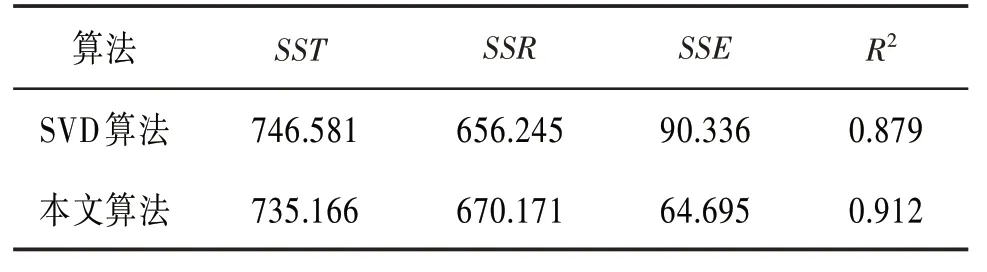
表2 兩種算法的離差及樣本決定系數

對線性回歸方程的顯著性檢驗，除采用上述樣本決定系數外，還可以根據P 值做檢驗。P 值檢驗法的原則是當P 值小于給定的顯著性水平α 時，拒絕原假設H0。P 值檢驗法具有可比性，不需要查表（只需用P值與顯著性水平α相比較）等優點〔12〕。

為進一步驗證本文算法的有效性，對上述兩個回歸方程采用P值檢驗法分別進行了顯著性檢驗。

設顯著性水平α=0.05，兩個回歸方程得到的P值分別為0.033 6、0.027 4，其統計學含義是：接受“五個自變量x1,x2,…,x5整體對因變量y 產生顯著線性影響”的判斷，犯錯誤的概率為0.033 6、0.027 4。

這兩個P 值都低于顯著性水平α，故兩個回歸方程都為顯著，但本文算法得到的回歸方程犯錯誤的概率更低。

4 結束語

基于一元及多元線性回歸的平差模型，引入總體最小二乘法回歸參數的一種新迭代算法。該算法理論依據充分，迭代格式簡潔，容易編程實現，并且同時考慮到自變量系數矩陣的觀測誤差和因變量的觀測誤差，得到的回歸方程更加合理可信。通過算例實測分析，該迭代算法得出的回歸模型具有良好的擬合效果，可以實際應用于數據測量、金融、統計分析等方面的回歸分析建模。