Python語言在Liu混沌系統仿真實驗中的應用

于清文 趙海濱 顏世玉

摘 ? 要：以Liu混沌系統為例，采用Python語言進行建模和仿真，并利用matplotlib繪制狀態變量的響應曲線、二維相圖和三維相圖。采用Python語言進行混沌系統的仿真，非常方便和直觀，能夠加深學生對理論知識的理解和掌握。

關鍵詞：混沌系統 ?仿真教學 ?Python語言

中圖分類號：G642.1 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A ? ? ? ? ? ? ? ? ? ? ? 文章編號：1674-098X（2020）04（c）-0139-02

Abstract：Taking Liu chaotic system as an example， we use Python language to model and simulation， and use matplotlib to draw the response curve， two-dimensional and three-dimensional phase diagram of state variables. It is very convenient and intuitive to use Python language to stimulate chaotic system， which can deepen students understanding and mastery of theoretical knowledge.

Key Words：Chaotic system; Simulation training; Python language

混沌及其應用技術是近年來非線性科學領域的熱點問題[1]。混沌系統對初始條件非常敏感，廣泛存在于各種非線性系統中。1963年氣象學家Lorenz在三維自治系統中發現了第一個混沌吸引子。劉崇新等提出了Liu混沌系統，能夠用硬件電路實現，具有非常豐富的動力學特性和廣泛的應用[2]。

本文以Liu混沌系統為研究對象，采用Python語言進行建模和仿真。在仿真實驗中，根據Liu混沌系統的狀態方程，采用歐拉方法進行仿真，并通過matplotlib庫進行數據的可視化。該仿真實驗非常的方便和直觀，能夠激發學生的學習興趣，加深學生對理論知識的理解和掌握。

1 ?Python語言

Python語言簡單易學，而且具有開源和免費的優點，是目前最受歡迎的程序設計語言之一。越來越多的大學和科研機構將Python作為首門程序設計課程的教學語言[3-4]。Python是一種跨平臺的解釋型、面向對象、動態的高級程序設計語言，有大量的開源庫可供調用[5]。matplotlib是Python經典的二維繪圖庫，可以很容易的繪制折線圖、柱狀圖和散點圖等二維圖像，非常方便的進行數據可視化[6]。在matplotlib庫中，通過函數Axes3D繪制數據的三維圖形。

2 ?Liu混沌系統

Liu混沌系統的結構簡單，能夠用硬件電路實現[7]。Liu混沌系統的狀態方程表示為

（1）

其中，x，y和z為Liu混沌系統狀態變量，a，b，c和d為常數。當a=10.0，b=40.0，c=2.5和d=4.0時，Liu混沌系統為混沌狀態。Liu混沌系統具有三個不穩定的平衡點，分別為，和。

3 ?Liu混沌系統的仿真

歐拉方法是一種簡單的數值積分方法，數值收斂性好。在歐拉方法中，將時間區間[0，T]做N等分，小區間的長度h=T/N稱為步長。采用歐拉法進行Liu混沌系統仿真，Python語言腳本程序如下

在腳本程序中，對Liu混沌系統的參數和初始狀態進行設置。Liu混沌系統的初始狀態設定為。采用歐拉方法進行仿真時，步長設定為h=0.001，仿真時間設定為50s。在matplotlib庫中通過函數Axes3D繪制三維圖形。

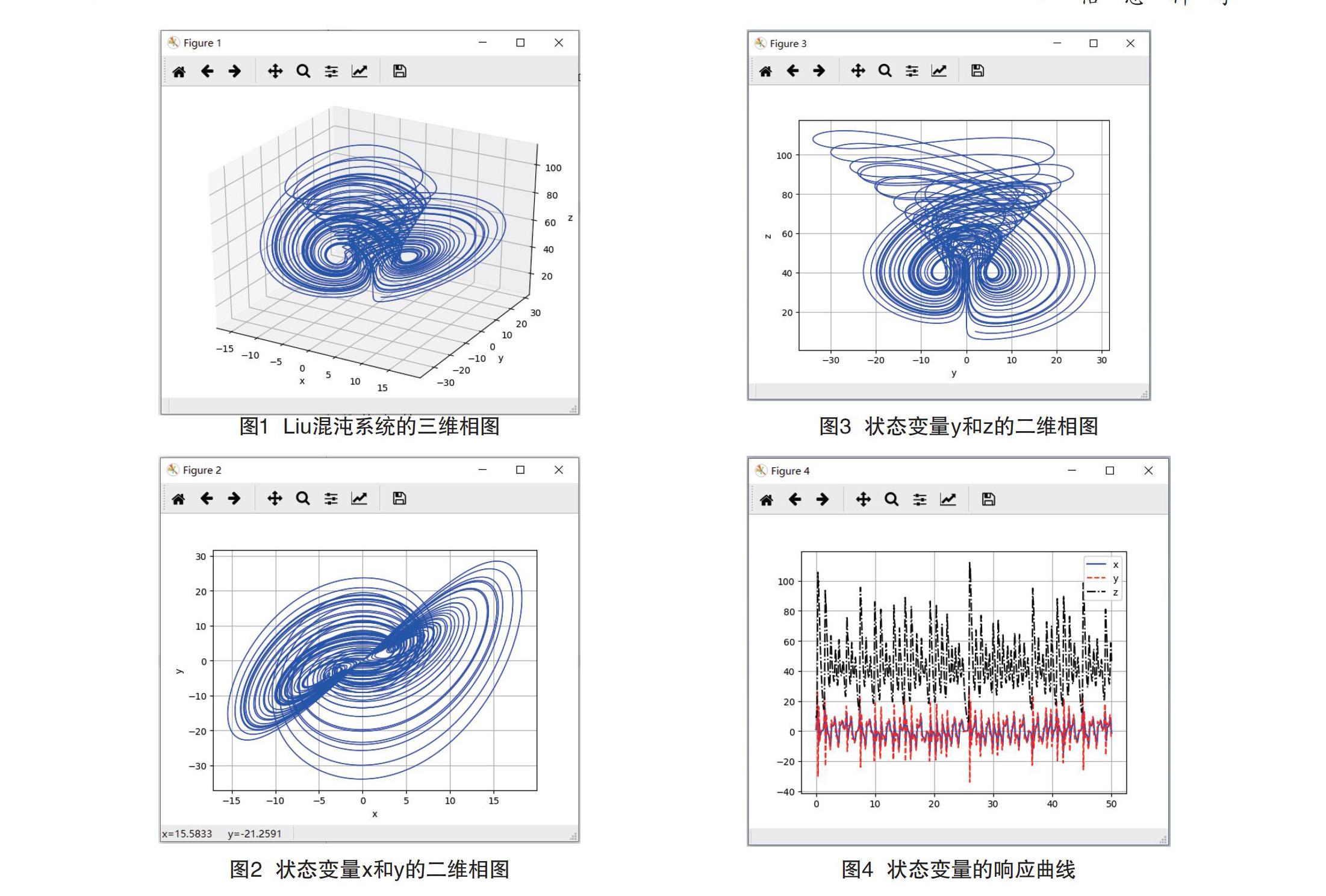
該腳本程序運行后，可以得到Liu混沌系統的三維相圖，如圖1所示。Liu混沌系統狀態變量x和y的二維相圖，如圖2所示，狀態變量y和z的二維相圖，如圖3所示，狀態變量的響應曲線，如圖4所示。Liu混沌系統處于混沌狀態。

4 ?結語

Python語言具有非常高的編程效率，在機器學習、數據挖掘和模式識別等領域具有廣泛的應用。根據Liu混沌系統的狀態方程，本文采用Python語言進行Liu混沌系統的建模和仿真，采用matplotlib繪制三維相圖、二維相圖和狀態變量的響應曲線。采用Python語言進行混沌系統的仿真，非常形象和直觀。學生可以修改參數和腳本程序，然后進行仿真實驗，觀察仿真結果，能夠加深學生對理論知識的理解和掌握。

參考文獻

[1] 孫克輝. 混沌保密通信原理與技術[M]. 北京：清華大學出版社，2015.

[2] 高秉建. 基于Liu混沌系統生成的多翅膀蝴蝶吸引子[J]. 復雜系統與復雜性科學，2016，13（1）：91-94.

[3] 嵩天，黃天羽. Python語言程序設計教學案例新思維[J].計算機教育，2017（12）：11-14.

[4] 楊榮領.《Python語言程序設計基礎》課程教學改革實踐[J]. 高教學刊，2019（3）：135-137.

[5] 張健，張良均. Python編程基礎[M].北京：人民郵電出版社，2018.

[6] 張若愚. Python科學計算[M].北京：清華大學出版社，2012.

[7] 王發強，劉崇新. Liu混沌系統的混沌分析及電路實驗的研究[J]. 物理學報，2006，55（10）：5061-5069.