基于常規測井資料計算煤層力學參數

陳東銳，王延斌，韓文龍，王 力

（1.中國礦業大學（北京）地球科學與測繪工程學院，北京 100083；2.中聯煤層氣有限責任公司晉城分公司，山西 晉城 048000）

煤儲層巖石力學參數（泊松比、彈性模量等）是應力場模擬、儲層壓裂改造設計的基礎參數［1］。橫波資料也是各類工程參數準確計算的基礎［2］。對于縱波和橫波速度的重建，前人做了很多研究。李敬功在Xu-White模型的基礎上，建立了以空間模量差值比為基礎的橫波時差擬合模型［3］。馬中高將Gardner公式進行了推廣，建立了密度與縱、橫波速度的關系式［4］。上述一系列研究成果多集中在常規砂泥巖地層，針對煤儲層的橫波時差構建方法尚不多見。本文在已有的針對砂泥巖地層的橫波速度估算方法的基礎上，構建適合于煤巖層段的橫波時差計算方法，搭建起巖石力學參數計算的橋梁，能夠在計算得出研究區煤儲層各項巖石力學參數基礎上，揭示縱向上連續的煤儲層力學性質參數及其變化特征，為煤儲層集中射孔壓裂施工提供基礎數據。

1 研究區塊概況

本次研究的柿莊北區塊位于沁水盆地南緣沁水復向斜東翼東部緩坡帶，目標煤層3號煤層位于山西組底部，埋深800～1000m，發育穩定，平均厚度5.45 m，儲層壓力梯度介于0.61～0.859MPa/100m，煤層儲層溫度介于27.5～30.27℃，平均孔隙度為5.63%，滲透率為0.085×10-3μm2左右，平均含氣量17.11 m3/t，本區塊煤層氣擁有較好的開發潛力［5］。

2 構建橫波時差擬合模型

對于密度與縱、橫波速度的關系，不同研究者針對不同巖性的巖石，提出了不同的經驗公式。但是巖石本身比較復雜，而且不同區域變化不一，煤層的地質特征與砂泥巖地層有很大的不同。為探索研究區煤巖層段縱、橫波時差及密度測井之間內在相關性，選取本區已經進行過多極陣列聲波測井的井作為標準井，提取其煤巖層段縱、橫波時差和密度測井數據，分別構建了橫波時差與縱波時差、橫波時差與密度測井數據的交會圖（見圖1、圖2）。

圖1 縱波時差-橫波時差交會圖

圖2 密度-橫波時差交會圖

從圖1、圖2中看出，煤巖層段的橫波時差與縱波時差、橫波時差與密度測井相互之間具有較好的線性相關性。擬采用縱波時差、密度測井為參數對橫波時差進行擬合，并建立多元擬合模型。

Gardner（1974）［6］提出了對各種巖石平均的縱波速度與密度（ρ）的函數形式 ρ＝AVpB。因此，對于煤巖層段的橫波時差與縱波時差、密度測井采用多元非線性模型來進行擬合，得出方程（1），R2＝0.91。

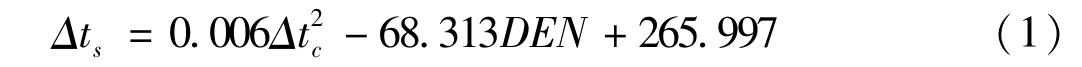
利用建立的多元非線性模型方程（1）進行計算得出的橫波時差與實際測量值相比結果如圖3所示，其相對誤差介于0.12～10.17，平均相對誤差為5.14。

圖3 密度和橫、縱時差擬合模型結果與實測數據比較

3 煤層力學參數計算與分析

通過巖石力學試驗只能獲得單個層位巖石力學參數，而利用測井資料可以獲得連續的巖石力學參數，并且能夠顯示縱向上力學性質的連續變化特征。巖石形變主要力學參數包括泊松比、剪切模量以及彈性模量等［7］，上述各種力學參數可由縱波時差Δtp、橫波時差 Δts和巖石密度ρ計算求得。

選取研究區某井主力煤層3＃煤層井段進行分析研究。某井3＃煤層埋深1497.00～1502.80m，平均縱波時差為131.7μs/ft，平均橫波時差為211.7μs/ft，平均縱橫波速度比為 1.61，平均密度值為1.30g/cm3。提取本井3＃煤層段的縱波時差與密度測井響應值代入方程（1）進行計算，可以得出其剪切模量在2.21～4.77GPa范圍變化，平均值為2.87GPa；泊松比值在0.26～0.37范圍變化，平均值為0.32；彈性模量在4.15～16.32GPa范圍變化，平均值為7.64GPa。

本井段取煤樣5塊進行室內力學實驗，試驗采用RMT-150B巖石力學實驗系統，得到實驗結果如表1所示。可以看出，測井解釋成果與室內實驗獲得力學參數基本一致。

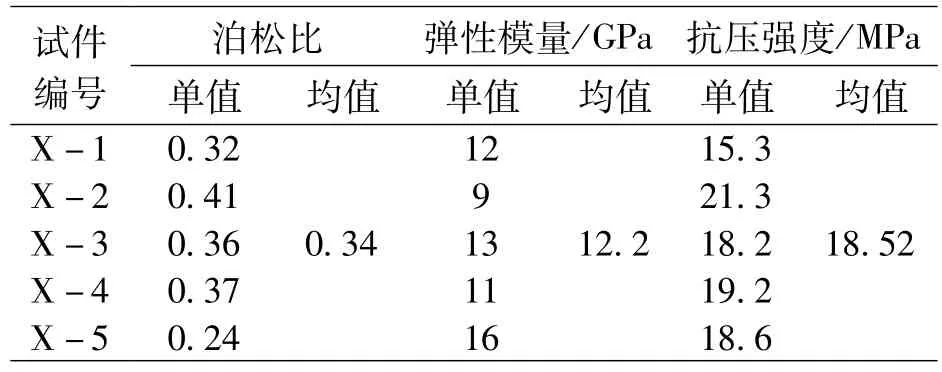
表1 實驗室力學參數實驗結果

4 結論

1）運用縱波、密度測井與橫波時差的關系構建擬合模型較為簡單、便捷，免去了中間參數值的計算，避免了參數值計算不準確而引起的誤差，且模型相關系數較高為0.91，計算結果精度也比較高。然而，對于不同煤層，不同的研究區域，擬合模型是否能推廣使用，還需要進一步分析與驗證。

2）在煤層力學參數計算中，目標煤層剪切模量在2.2～4.4GPa范圍變化，泊松比值在0.07～0.26范圍變化，彈性模量在4.15～16.32GPa范圍變化，計算所得力學參數與實驗室測試結果基本一致，計算得出的縱向上連續的力學參數也能夠為后期施工提供數據基礎。