周向波紋圓柱殼屈曲特性研究

徐 戎，張 山，李勝秋

（1.招商局重工（江蘇）有限公司，江蘇 南通 226116；2.江蘇科技大學機械工程學院，江蘇 鎮江 212003）

潛水器是深海探測重要科學工具，耐壓殼是潛水器的關鍵部件，其質量占潛水器總質量的1/4～1/2［1］，它能承受海水的巨大壓力，為工作人員提供安全的工作環境，使設備正常工作。柱形殼是一種常用的耐壓結構，其特點是空間利用率高、流體運動阻力小、制造方便。但是這些圓柱殼在承受外壓時容易發生屈曲，往往導致無法恢復的坍塌。

一般來說，存在許多提高圓柱殼屈曲能力的方法。首先，改變子午線形狀是一種有效的方法。例如，Blachut和其同事研究發現等質量的桶形殼具有比未加筋圓柱殼更高的屈曲能力［2-3］。最近，張建等人，研究了卵形殼及其在海洋工程中的應用［4］，發現長卵形壓力殼對屈曲行為具有有效的抵抗。另一種方法是添加加強筋或波紋來提高圓柱殼的屈曲能力［5］。在這些加強方法中，波紋加強是最優的選擇，其不需要額外的加強筋就能夠提高柱形殼的屈曲能力。Ross等［6］對周向波紋圓柱形耐壓殼的非線性屈曲進行了理論、數值和試驗研究，Ghazijahani等［5］采用試驗法研究了波紋個數對周向波紋圓柱殼屈曲特性的影響。但是，上述研究都是基于相同幅值的波紋柱殼，對不同幅值的波紋柱殼研究較少。

因此，本文討論了在均布外壓下波紋圓柱殼的屈曲特性。設計了1個普通圓柱形耐壓殼和2個周向正弦波紋柱形耐壓殼，并且采用數值分析的方法研究線性屈曲、非線性屈曲以及波紋幅值對柱殼的影響規律。

1 周向波紋柱殼幾何模型

波紋柱形耐壓殼模型的結構示意圖如圖1所示。波紋柱形耐壓殼的具體幾何參數列于表1中，波紋柱殼的幾何參數：模型的直徑D＝160 mm，高度H＝230 mm，壁厚t＝2 mm，正弦波紋均勻的分布在柱形耐壓殼上，波紋的幅值s＝0 mm，2.5 mm，5 mm，當波紋柱形耐壓殼的幅值s＝0mm時，此柱殼為普通柱殼，波紋的跨距S＝20 mm，金屬密封蓋厚度T＝10 mm。

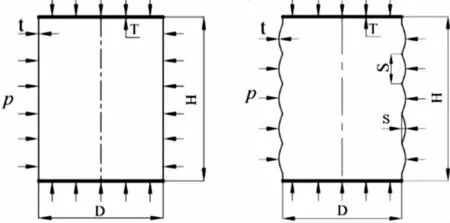
圖1 柱殼模型幾何外輪廓Figure 1 geometric outline of cylindrical shell model

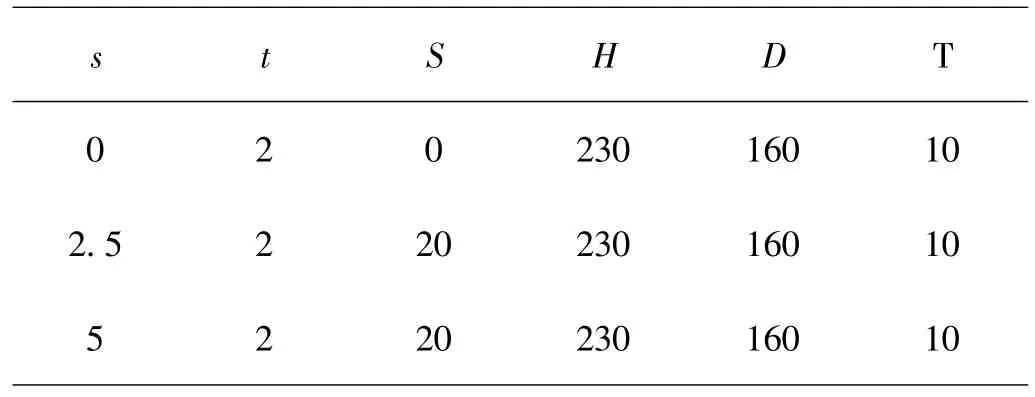
表1 柱殼的幾何參數Table 1 geometric parameters of cylindrical shell mm

2 有限元分析

2.1 數值模型

本章選用ABAQUS/Standard對柱殼進行屈曲分析。它可以分析簡單的線性分析，也可以進行大型的、復雜的非線性分析。首先，一般使用Solidworks軟件對普通耐壓殼和周向正弦波紋柱形耐壓殼進行三維建模，把建好的模型保存為相應格式，接著把模型導入ANSA軟件中、對柱殼劃分網格，先要對模型進行TOPO操作，即對導入的模型縫合；因為柱殼的主體壁厚與其密封蓋的厚度不同，所以在劃分網格后要對其設置不同的PID，這樣方便在ABAQUS中設置模型的幾何參數。如圖2所示，柱殼的兩端的網格要呈錢幣形狀，即柱殼兩端要使用錢幣形的網格劃分方式，這樣才能更好的保證數值計算的準確性。

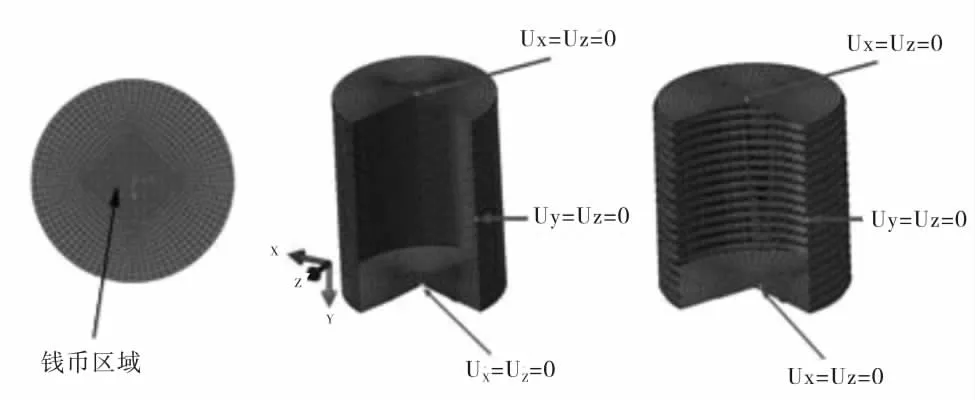
圖2 柱形耐壓殼的數值模型Figure 2 numerical model of cylindrical pressure shell

有限元模型利用全集成殼單元S4來避免沙漏。由于本文研究的柱形耐壓殼是薄殼，故單元屬性選擇為殼單元。柱形耐壓殼都賦予相同的材料參數，在圓柱殼的外表面施加單位均布壓力 ，這里 P＝1MPa。圖2是有限元模型的邊界約束條件。由CCS2018［7］可知，工作時的柱形耐壓殼不受約束。當對其進行整體計算時，耐壓殼體需要3個支撐點，約束殼體在6個方向上的位移分量，邊界條件需要對稱設置：U x＝U z＝0，U y＝U z＝0，U x＝U z＝0，以上設置不僅可以消除耐壓殼體的整體剛體位移，又不妨礙殼體的相對變形。

其中，波紋柱形耐壓殼主體的材料參數為［8］：彈性模量E＝2122.92MPa，泊松比μ＝0.3284，抗拉強度為33.8～40.2MPa。此仿真即分析了波紋幅值對柱形耐壓殼屈曲的影響，又分析了普通柱形耐壓殼與波紋柱形耐壓殼的屈曲性能。

2.2 數值計算結果分析

1）理想殼體的屈曲分析。本節有限元模型分析步設置如下：選用ABAQUS對波紋柱形耐壓殼展開線彈性分析，選擇Step中的Linear perturbation選項，然后在選項列表中設置Buckle作為線彈性分析步，并且設置特征模態階數為6階。ABAQUS提供了兩種方法來提取特征值：Lanczos算法和Subspace iteration算法。這兩種算法的使用范圍不一樣，當需要求解的特征模態階數較高時一般推薦使用Lanczos算法；如果僅僅求解少量的特征模態（少于20階特征模態）時，則使用Subspace iteration算法的速度可能更快。在此項分析中，將使用Subspace iteration算法，并計算出有限元模型的前6階特征值與屈曲模態。

柱殼的線性分析結果如圖3和表2所示。圖3呈現出1個普通柱殼與2個正弦波紋柱殼的屈曲模式，三個柱殼均在其中間位置發生失穩；當波紋幅值s＝0mm，2.5mm，5mm時，它們的失穩波數分別為：5個、4個、3個。

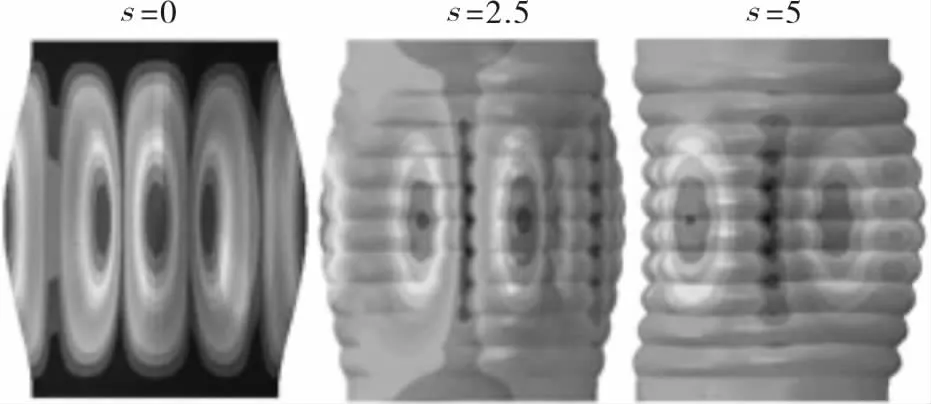
圖3 理想柱殼屈曲模式Figure 3 buckling mode of ideal cylindrical shell

從表2中發現，波紋柱形耐壓殼的線性屈曲壓力隨著波紋幅值增大明顯提高。這種增強可以歸因于這樣的事實，即與普通耐壓殼的無限子午半徑相比，波紋柱形耐壓殼的局部子午半徑顯著減小了。結果表明，從平板到曲面，殼體的子午曲率越高，其承載能力越高。此外，屈曲波的減小可能是由于波紋柱形耐壓殼的極高剛度導致的。

表2 理想柱殼線性屈曲載荷（Plb）Table 2 linear buckling load of ideal cylindrical shell（Plb）

由表2中看出，隨著波紋幅值的增加，柱殼的線彈性屈曲載荷由100.06kPa增加到211.25kPa，表明在均布外壓作用下，周向波紋柱殼線彈性屈曲的抗壓性能優于普通柱殼。

2）真實殼體的屈曲分析。為了檢驗理想殼體屈曲失穩模式是否正確，要建立真實殼體的屈曲分析。首先，根據表1中的幾何參數制作實物模型，每種模型制作2個，共計6個。然后對已經制作好的實物模型進行3D外輪廓掃描，將掃描完成的外輪廓保存為相應的格式，導入ANSA中進行網格劃分，如圖4所示，為普通柱殼掃描完成后的視圖。

圖4 三維輪廓掃描試驗Figure 4 three dimensional contour scanning test

選用ABAQUS中的Static，Riks分析步對柱殼進行非線性分析，非線性屈曲值用Pnlb表示。由于掃描完成的模型中已經包含了初始幾何缺陷，所以對真實殼體進行屈曲分析更能反映實況下殼體的失穩模式。

圖5是真實柱殼的后屈曲模式，表3呈現了真實柱殼的線性屈曲載荷。

圖5 真實柱殼的后屈曲模式Figure 5 post buckling mode of real cylindrical shell

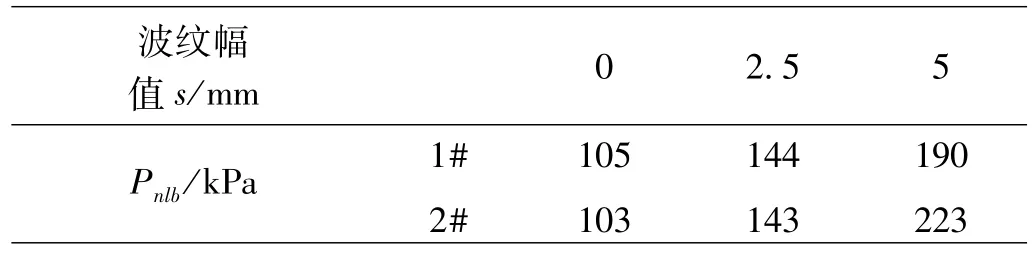
表3 真實柱殼的非線性屈曲載荷（Pnlb）Table 3 nonlinear buckling load of real cylindrical shell（Pnlb）

由表3可知，相同波紋幅值柱殼的非線性屈曲載荷基本一致，表明實物模型制作精度較高；并且隨波紋幅值的增大，非線性屈曲載荷也逐漸增大，這與理想柱殼線性屈曲載荷有相同的規律，而且線性載荷值與非線性載荷值高度吻合，說明線性屈曲分析的可靠性。

圖5是真實柱殼的后屈曲模式，相同波紋幅值柱殼的后屈曲模式吻合度較高；并且圖5的后屈曲模式與圖3線性屈曲模式一致，失穩位置都是在柱殼的中間位置，這是典型的失穩模式。

3 結論

1）設計了一種周向波紋圓柱殼，隨著波紋幅值增大，波紋柱殼抗屈曲的能力也隨之增大，并且屈曲載荷增幅很明顯，當波紋幅值s＝5 mm時，其線性載荷與非線性載荷均為普通柱殼（s＝0 mm）的2倍多。2）理想柱殼線性屈曲載荷值與真實柱殼非線性屈曲載荷值高度一致，說明了線性屈曲分析的可靠性，并且柱殼線性失穩模式與非線性失穩模式吻合良好。