小學“數學廣角”單元教學中的數學思想滲透

黃兆光

摘要：“數學廣角”作為人教版數學教材編排的一大特色，其對發展學生的數學思想，培養學生的應用意識、解決實際問題的能力以及學生的數學核心素養，都有著積極的作用。文章以人教版五年級上冊的“數學廣角”——“植樹問題”的教學為例，通過展示部分教學片斷，分析如何利用“植樹”問題向學生滲透建模思想，以使學生觸類旁通、舉一反三。

關鍵詞：小學數學;“數學廣角”;數學思想

一、小學“數學廣角”單元教學內容的特點

“數學廣角”這一單元內容是人教版數學教材的一大特色，從二年級到六年級，增設獨立于“數與代數”“圖形與幾何”“統計與概率”“綜合與實踐”這四大板塊的單元內容，它蘊藏著豐富的數學歷史、數學知識以及數學思想。教材編者煞費苦心特意編排這一內容，旨在通過數學廣角的教學，循序漸進地、系統地向學生更好地滲透相關的數學思想，引導學生發現數學與生活的緊密聯系，培養學生的實際運用能力，促使數學核心素養的落實。

“數學廣角”的教學內容比較靈活，兼具開放性與挑戰性，并非簡單計算便能得出答案，需要學生經歷猜想、操作、驗證等系列過程，這有利于學生的體驗與感悟其中蘊含著的數學思想。此外，數學廣角教學內容貼近現實生活，將復雜、抽象的數學思想寓于學生常見的生活情景中，既增強了數學教學的趣味性，又易于調動學生的學習興趣，利于激發學生的好奇心和探究欲。

二、小學數學五年級上冊“植樹問題”中的數學模型思想滲透分析

模型思想是指從現實生活或具體情境中抽象出數學問題，用數學符號建立方程、不等式、函數等表示數學問題中的數量關系和變化規律，換句話說，即將客觀事物做抽象化的處理，從而建立起一個數學模型，根據這個數學模型有效分析事物本質規律的一種思維方法。

人教版五年級上冊“數學廣角”單元教學為“植樹問題”，這一問題涉及“兩端都植樹”“一端植樹”“兩端都不植樹”三種情況。

【教學片斷一】

師：同學們，請看看屏幕上的這道題，大家會做嗎？（多媒體出示題目：20米，每5米分一段，一共可分幾段？）

生（大部分學生快速回答）：4段。

師：正確，我們繼續挑戰，請繼續看題。這題的答案又是多少呢？（多媒體出示題目：20米路，每5米種一棵樹，一共可以種幾棵樹？）

生（多數）：4棵。

生（少數）：5棵。

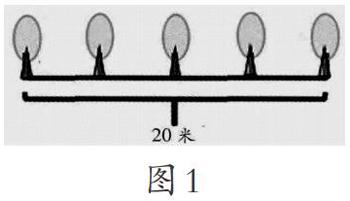
師：有同學說4棵，有同學說5棵，到底誰正確呢？請看屏幕。（多媒體出示圖1）

在備課時，筆者預測學生做“20米路，每5米種一棵樹，一共可以種幾棵樹？”這道題時會出現兩種不同答案，為此，筆者在實際教學中以此為契機，引發學生的認知沖突。另外，當出現兩種不同的答案時，筆者先告訴學生正確的答案，卻未告訴學生“為什么”，這有利于激發學生的求知欲，調動學生的主動性，促使其積極參與教學活動，主動探究新知。

【教學片斷二】

師：正確答案是5棵。真奇怪，兩道題目的表述好像都一樣呀，為什么一個答案是4，一個答案是5呢？下面，請同學們以小組的形式來“找茬”，認真討論這兩道題的異同點在哪里。

（經過討論，學生發表意見）

生：這兩道題的相同點：都是平均分。這兩道題的不同我們也找到了，前面一道題說的是“每5米分一段”，后面一道題說的是“每5米種一棵樹”。

師：好，關于不同點，老師覺得可以再精準一點，不同點在于“一段”與“一棵樹”，對嗎？

生：對。

師：那“一段”與“一棵樹”有什么不同呢？

生：“一段”有兩個點，“樹”是種在坑里的，所以“一棵樹”相當于一個點。

師：按道理說，“一段”有兩個點，“一棵樹”才一個點，那是不是段數比點多呢？

師：兩段有多少個點？三段呢？四段呢？五段呢？六段呢？—n段呢？

生：兩段有三個點，三段有四個點，四段有五個點，五段有六個點。n段有n+1個點。

師：所以是點多還是段多？段數和點有什么關系？

生：點比段數多1，點=段數+1。

師：在植樹問題里，“平均分的段”代表什么？

生：代表兩棵樹之間的間隔。

師：回答正確。所以，對于“20米路，每5米種一棵樹，一共可以種幾棵樹？”這道題，我們應該怎么算？

生：20÷5+1=5（棵）。

師生齊總結：植樹棵數=距離÷間隔+1。

在這一教學片斷中，筆者首先引導學生明白，“植樹”是植在點上，而不是植在段中;在此基礎上，筆者通過循序漸進的提問，逐步引導學生發現“段”與“點”的關系——點=段數+1，并使學生明確“段”代表樹與樹之間的距離。這樣，通過一連串問題的引導，學生在思考過程中不知不覺便在頭腦中建立起了“植樹問題”的模型思想：“植樹棵數=距離÷間隔+1”。建立了這一模型思想后，對于“植樹問題”，學生便能做到觸類旁通、舉一反三了。

【教學片斷三】

師：同學們請看屏幕的這幅圖，還是的同樣的條件，在這種情況下，可以植多少棵樹呢？（多媒體出示圖2）

生：4棵。

師：怎么算的？可以用我們剛才學習的“植樹棵數=距離-間隔+1”這個規律算嗎？

生：就是用“植樹棵數=距離÷間隔+1”這個規律算的，只不過算完之后要減去1，因為有一端被房子擋住了，不能種樹。

師：那出現這種情況呢？可以種多少棵？同學們又是怎么計算的？（多媒體出示圖3）

生：一共可以種3棵，還是可以用“植樹棵數=距離÷間隔+1”這個規律來計算，只不過左右兩端都被房子擋住了，所以算完之后需要減去2。

師：看來大家對植樹問題的規律掌握得不錯，能根據實際情況靈活變通運用。老師把同學們剛剛說的話重新整理一遍，大家仔細聽，看老師說的對不對。一端能種樹，一端不能種樹的情況下，種樹規律則為“植樹棵數=距離-間隔+1-1”，也就是“植樹棵數=距離÷間隔”;兩端都被擋住，即兩端都不種樹的情況下，種樹規律為“植樹棵數=距離÷間隔+1-2”，也就是“植樹棵數=距離÷間隔一1”。老師說清楚了嗎？是不是這個意思？

生：對，就是這個意思。

師：好，老師想請同學們與老師一起來總結一下這三個種樹規律，有信心嗎？

師生齊總結：兩端都種樹：植樹棵數=距離÷間隔+1。一端種樹：植樹棵數=距離÷間隔。兩端都不種樹：植樹棵數=距離÷間隔-1。

在學生建立了一般植樹問題的模型思想后，筆者逐步引申出植樹問題的兩種特殊情況，引導學生在運用植樹問題模型思想解決問題的過程中，總結出“一端植樹”和“兩端都不植樹”的數學規律。另外，在教學時，筆者用簡練的語言復述學生的話，并請學生判斷筆者說得對不對，這有利于集中學生的注意力，促使學生積極參與課堂教學;而最后師生齊總結三種不同的植樹方式的規律時，有利于學生整理自己的思緒，回顧教學內容，鞏固新知。

【教學片斷四】

師：植樹問題規律可以運用在其他地方嗎？

生1：路燈的安裝。

生2：公交站的設定。

生3：鋸木頭也可以用，屬于兩端都不種樹的情況。

生4：爬樓梯是屬于一端種樹的情況。

模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑。筆者讓學生通過頭腦風暴的形式，把植樹問題的模型思想與生活聯系起來，引導學生發現數學知識與生活聯系的緊密性，讓學生學會學以致用，將理論與實踐結合起來。

三、結語

人教版小學數學中“數學廣角”的教學內容，緊貼生活實際，雖然教起來有一定的難度，但其蘊含著豐富的數學思想，教師需要予以重視，不可因其難教便敷衍了事，不僅需要精心研讀教材，更要做到“備學生”，引領學生經歷“觀察、分析、歸納、推理”等活動，使學生從中感悟到相關的數學思想，并靈活運用數學思想。

參考文獻

[1]中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.

[2]蒙澤穎.小學高年級“數學廣角”單元滲透數學思想方法的教學策略研究——以人教版教材為個案[D].貴陽：貴州師范大學，2019.