基于改進鯨魚算法的并網型微網能量管理

謝 姿, 張惠娟, 劉 琪, 李玲玲

(河北工業大學省部共建電工裝備可靠性與智能化國家重點實驗室，天津 300130)

微電網的拓撲結構因設備類型和運行模式的不同可分為并網型和獨立型[1]。并網型微電網可以與外部電網聯網運行，具備并離網切換與獨立運行能力[1]。然而，分布式電源中的風機和光伏發電具有很強的隨機性和間歇性，嚴重影響電力系統的正常運行和供電網絡的可靠性[2]。因此并網型微網中分布式電源(distributed generation,DG)的能量管理十分關鍵。

文獻[3]建立了添加蓄電池全壽命周期成本的經濟模型，利用多種群遺傳算法對模型求解；文獻[4]使用熵權法對多目標函數歸一化處理，選用改進的仿電磁學算法(ELM)求解該優化問題；文獻[5]綜合供電可靠性和環保效益建立獨立微網經濟模型，結合改進的粒子群算法對該經濟模型求解；文獻[6]建立了以總凈現費用為經濟性優化目標和以年二氧化碳排放量為環保性優化目標的多目標優化配置模型，采用改進的非劣排序遺傳算法(NSGA-II)對某算例進行仿真計算。

前人研究多以獨立微網為研究對象，缺少對風光柴儲網分布式發電系統能量管理的探索，忽略季節天氣對容量配置問題的影響，可能存在調度策略應用不廣泛的情況，最重要的是，應用算法較為傳統，結果可能導致其在微網能量管理應用中的全局收斂能力和尋優能力欠缺。對此，建立并網型微網容量配置模型，采用混合差分排序的優化和變異算子隨機調整差分變異策略且引入Lévy飛行軌跡機制來改善標準鯨魚算法(WOA)的收斂精度和收斂速度。選擇某地一年四季4個典型日進行案例分析，驗證模型和算法的廣泛有效性。

1 并網型微網容量優化配置模型

1.1 等日值投資成本

f1=CDG+COM+CR+CF

(1)

式(1)中：CDG為分布式電源的初始投資成本，也稱安裝成本，包括風力發電、光伏發電、儲能系統和柴油發電機的購置成本；COM為運維成本，是微網運行過程中維護設備所投入的人力物力成本；CR為替換成本，表示在微網的設計使用周期內更換設備產生的費用；CF為柴油機的燃料消耗成本。

各部分成本進行等日值表示如式(2)所示：

(2)

1.2 與電網交互的成本

(3)

式(3)中:CE為與電網交互的成本；Psell(t)為售賣給電網的電量；Pbuy(t)為向電網的購電量;kbuy為向電網購置的電價;ksell賣給電網的電價。

并網型微網，可以通過大電網將微網產生的多余的電能消納或是通過向大電網購電緩解微網中電能嚴重不足的情況，因此在并網型微網中與大電網的交互費用是不可忽略的。

1.3 環境污染懲罰費用

風力和光伏發電屬于清潔能源，不產生污染廢氣。柴油發電機在運行時會產生CO2、SO2、NO等廢氣，治理這些廢氣所需要的費用即為環境治理費用也作為一項目標函數。

(4)

式(4)中：uj為第j種廢氣的處罰金；vj柴油機單位功率下第j種廢氣的排放量。

1.4 約束條件

微網系統中不同的設備要在一定的約束條件內運行，滿足不平衡約束的同時還要滿足電能的平衡約束，具體約束條件如式(5)所示：

(5)

2 調度策略

在某一時刻光伏發電系統和風力發電系統超出或少于負荷的不平衡功率為

ΔP(t)=Pw(t)+Ppv(t)-Pload(t)

(6)

式(6)中:ΔP(t)為儲能電池和柴油發電機沒有投入運行時系統的不平衡功率。

首先根據當日的氣象數據計算新能源設備的實時輸出功率，微電網系統優先將新能源設備產生的電能供給電負荷，然后根據式(6)計算不平衡功率，如果新能源設備的輸出功率無法滿足電力負荷需求，儲能系統進入放電狀態，此時判斷釋放的電能是否會低于蓄電池約束下限，如果低于電能下限，則需要向電網購入電能，如果向電網購入的電能超過購買上限，柴油機作為最后一道電源啟動，保證供電可靠性；反之，如果新能源設備的輸出功率大于電力負荷需求，儲能系統進入充電狀態，此時需要判斷充入的電能是否會超過蓄電池荷電狀態和充電功率的約束上限，如果超過限制，則需要向電網售出電能。調度流程圖如圖1所示。

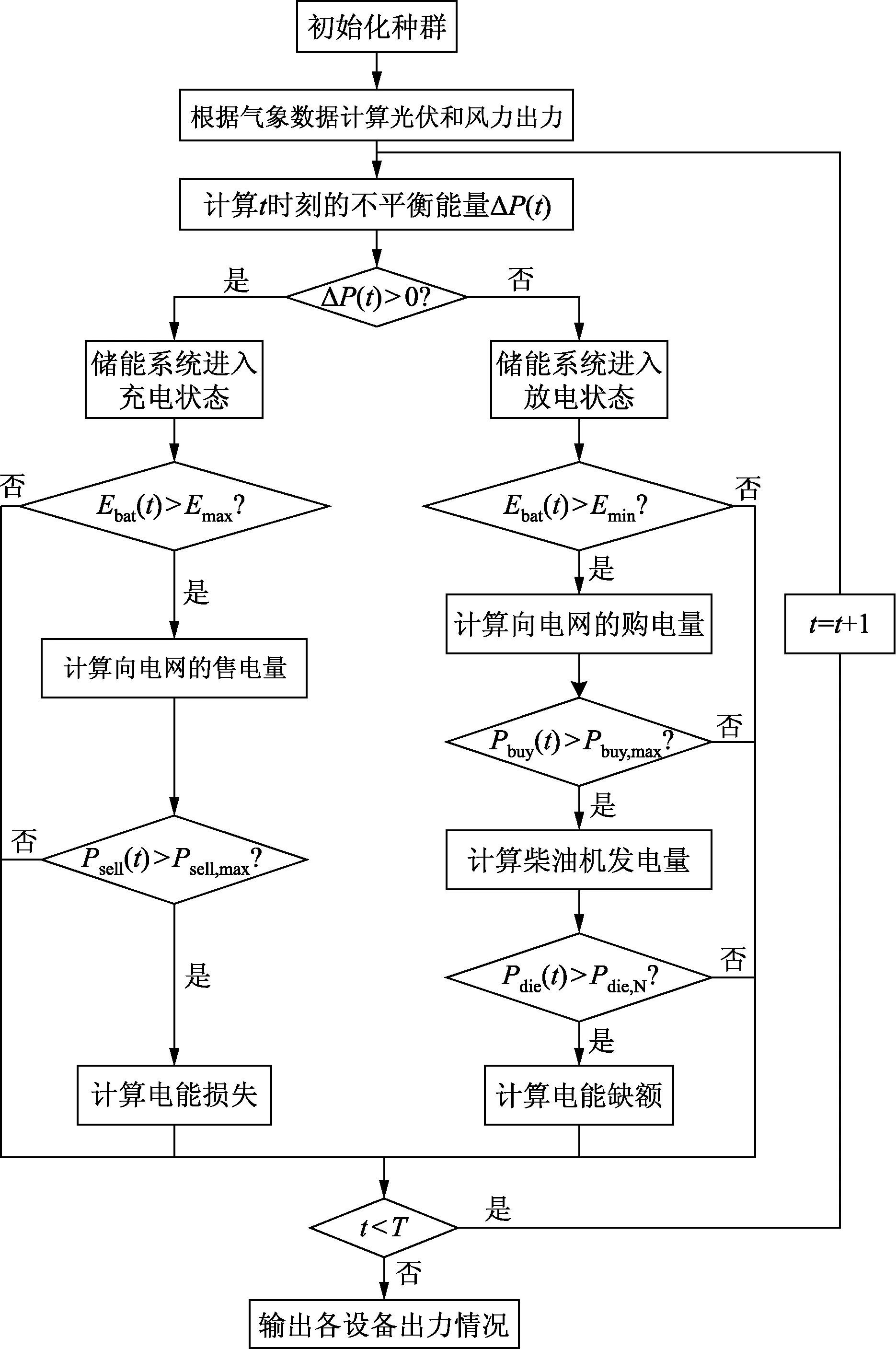
圖1 調度流程圖Fig.1 Scheduling flow chart

3 改進的鯨魚算法

3.1 標準的鯨魚算法

3.1.1 包圍捕食

(7)

式(7)中:g表示當前迭代;X*(g)和X(g)分別表示第g代中最好的鯨魚的位置(獵物的位置)和當前鯨魚的位置;r為[0,1]的隨機向量;a為收斂因子；X(g+1)表示更新后的鯨魚位置。

3.1.2 氣泡捕食

在鯨魚位置和獵物位置之間使用螺旋方程如式(8)模擬座頭鯨的螺旋狀移動。

(8)

式(8)中:l為[-1,1]的隨機數;b為螺旋形常數。

鯨魚捕食的過程當中，包圍捕食和氣泡捕食各有1/2的概率，其數學模型如式(9)所示

(9)

3.1.3 搜索獵物階段

當|A|≥1，鯨魚將放棄最好的鯨魚位置而隨機搜索獵物來更新位置，避免局部最優，進行全局搜索。

(10)

式(10)中：Xrand為隨機選取的鯨魚個體位置向量；X(g+1)表示更新后的鯨魚位置。

3.2 混合差分排序的優化策略

鯨魚算法操作簡單，易于編程且算法參數較少，但在求解優化問題時，能獲得較高的求解精度的基礎上擁有快速的收斂速度是一個關鍵問題。在標準WOA算法位置更新之前，將差分排序選擇優勢種群與基本WOA結合起來，加快收斂速度，使算法能夠以更大的概率快速尋找到全局最優解。

(1)排序：為了從種群中挑選良好的鯨魚個體，依據個體相關的適應度對每只鯨魚進行排序，從最優適應度到最差是適應度值，Ffiti表示第i只鯨魚個體的適應度。

(2)選擇概率：對每只鯨魚個體的排序完成后，第i只鯨魚個體被選擇的概率Pi可以表示為

(11)

3.3 差分變異策略

標準WOA算法在前期進行隨機全局搜索時，隨著迭代次數的增加，所有的鯨魚慢慢向歷史最右鯨魚位置移動，使得所有鯨魚位于同一局部最優位置附近，因此受到差分算法(DE)的啟發，引入隨機差分變異策略，對群體進行擾動操作，產生具有多樣性的新個體，幫助算法降低陷入局部最優的可能性。利用第t′代中最好的鯨魚個體、當前鯨魚個體和隨機選擇的鯨魚個體，其表達式為

X(t′+1)=X*(t′)+F[Xα-X(t′)]

(12)

式(12)中:Xα為群體中隨機選擇的鯨魚個體;F為變異算子。將其設置為以迭代次數為自變量的函數：

(13)

式(13)中：F0為常數因子；gmax為最大迭代次數。在算法開始時自適應變異算子具有較大值，在初期保持個體多樣性。隨著算法進展變異算子逐步降低，到后期變異率接近F0，該策略能夠保留優良信息，避免最優解遭到破壞。

3.4 引入Lévy飛行軌跡的優化策略

鯨魚算法在迭代后期存在易陷入局部最優的缺陷從而導致算法過早收斂而沒有收斂到較為精確的值。為了使算法提高全局收斂能力而跳出局部收斂提高算法的精確度，在算法后期進行局部開發時，引入Lévy飛行軌跡機制，從而提高種群多樣性，有助于提高算法跳出局部最優的能力。鯨魚進行所有的位置更新之后再進行一次Lévy飛行更新自身的位置，此位置的更新機制可以表述為

X(g+1)=X(g)+μsign(rand-1/2)⊕L(λ)

(14)

式(14)中:μ為服從正態分布的一個隨機數;rand為[0,1]的隨機數;L(λ)為Lévy隨機搜索路徑函數。

3.5 改進鯨魚算法的具體步驟

改進的鯨魚算法的流程圖如圖2所示。

圖2 算法流程Fig.2 Algorithm flow chart

具體的算法步驟如下。

初始化種群參數N，并根據適應度值記錄當前最優解及位置；

while (t

fori=1 toNdo

更新參數a,A,C,l,p的值；

種群根據適應度值進行排序，根據選擇概率Pi挑選優勢種群；

if (p<0.5)

if (|A|<1)

按照式(7)更新當前位置；

else if (|A|≥1)

按照式(10)隨機搜索獵物，并進行變異算子隨機調整差分變異策略；

end

else if (p≥0.5)

按照式(8)更新當前個體位置；

end

end

對于種群當中的每一個鯨魚個體按照Lévy飛行軌跡的優化策略再次更新位置；

計算種群中每個個體的目標函數值并更新全局最優個體及位置；

t=t+1;

end

4 案例分析

設定的最大年缺電概率fmax為0.1%，CO2、SO2、NO的排放系數分別為649、0.21、9.89 g/(kW·h)，治污費用分別為0.21、14.84、62.96元/kg；蓄電池最小剩余電量、最大剩余電量分別0.1、1，蓄電池的充放電效率相等，取90%；柴油價格為6.11元/L，微網中風機和光伏電池等其他微源的參數如表1所示。

表1 分布式電源的相關參數Table 1 Distributed power supply related parameters

4.1 典型日容量優化配置分析

由于天氣狀況對于并網向微電網DG出力具有一定的影響，本算例中從春夏秋冬四季分別挑選一天作為典型日來討論。目標函數為式(1)式(3)式(4)之和。春季、夏季、秋季、冬季容量配置結果如圖3～圖6所示。根據圖3～圖6中四個季節的溫度、光照和風速數據，按照光伏出力和風機出力模型[9-10]得到各時刻光伏和風力的輸出功率。當得到不可控設備的出力后，使用運行策略和改進算法來計算并網型微網的容量配置，仿真結果如表2所示。

春季和冬季屬于風大光小的情況，由于風機的輸出功率較大，所以只有在風速較小且太陽落山的情況下才需要蓄電池充放電或者向大電網購售電，幾乎不需要柴機油出力，配置結果分別如圖3、圖6所示；夏季屬于風小光大的情況，在白天風機和光伏共同承擔負荷的出力且光伏出力較大，在太陽落山之后主要依靠蓄電池充放電和向電網購售電，并且最后由柴油機保證容量優化配置的可靠性，具體配置結果如圖4所示；秋季屬于風光相差不大的情況，在白天風機和光伏共同承擔負荷的出力且風機出力較大，太陽落山之后主要依靠蓄電池充放電和向電網購售電且有柴油機最為保證微網正常運行的最后保障，與夏季相比，秋季用戶用電較少，負荷負載較小，故柴油機出力小于夏季，最終的容量配置成本也較低，具體的配置結果如圖5所示。

圖3 春季容量配置結果Fig.3 Spring capacity configuration

圖4 夏季容量配置結果Fig.4 Summer capacity configuration

圖5 秋季容量配置結果Fig.5 Autumn capacity configuration

圖6 冬季容量配置結果Fig.6 Winter capacity configuration

表2 四季的優化結果Table 2 Optimization results of four seasons

4.2 算法對比分析

仿真計算時，分別采用改進鯨魚算法(improved whale optimization algorithm， IWOA)、標準鯨魚算法(whale optimization algorithm, WOA)、差分算法(DE)和布谷鳥算法(CS)對并網型微網容量優化配置模型進行求解，對配置的最優目標函數值和運算效率對比。四種算法的目標函數值對比情況如表3所示。

由表3可以看出，改進的鯨魚算法在四個典型日都取得了最小的目標函數值，改進WOA求得的經濟成本比標準WOA平均節省了36.5%， 比DE平均節省了12.3%，比CS算法平均節省了7.7%。不同季節下的經濟成本差異較大，改進WOA在冬季的成本是四個季節中最低的，與成本最高的秋季相比少了81.6%的成本。說明改進的鯨魚算法能夠在容量優化配置的應用中獲得較為優越的最優解。

當四種算法都取迭代次數為300，種群個數為30時，它們的收斂曲線如圖7所示。且整體算例仿真的運行時間采用高可靠性和高可用性的小型機(Unix服務器)測量。

表3 算法的對比Table 3 Comparision of the algorithm

由圖7可見，相比于三種對比算法，改進的鯨魚算法在分布式電源優化配置的應用的收斂速度和收斂精度方面略優于其他三種算法。首先，改進WOA采用差分排序挑選優勢種群，是該算法在迭代初期就具備種群優勢；在春季，CS在第10代左右就取的最優解，可明顯其陷入局部最優，其他三種算法均在40～50代取得最優解且改進WOA的目標函數值最小；在夏季和冬季，四種算法的收斂代數近似，但是很明顯改進的WOA收斂精讀更高，可以跳出局部收斂，獲得更具有優勢的最優解；在秋季，改進的WOA收斂性和運行效率都具有明顯的優勢，總之，改進WOA算法在取得最優解的迭代次數以及全局收斂的能力均優于其他三種算法。

圖7 不同算法收斂曲線Fig.7 Convergence curve of different algorithms

5 結論

(1)提出了一種并網型微電網的能量優化管理方法。以等日值投資費用、環境懲罰費用和與電網交互的費用為綜合目標函數，考慮出力約束和蓄電池壽命，利用改進的WOA對容量配置模型求解。考慮天氣的影響，選擇一年四季4個典型日分別求解，說明了所提方法的有效性和改進算法的尋優能力，降低了系統的綜合發電成本，為并網型微網短期調度提供參考。

(2)采用混合差分排序的優化和變異算子隨機調整差分變異的策略且引入Lévy飛行軌跡機制來改善標準鯨魚算法的收斂精度和收斂速度，將改進的WOA算法應用于并網型微網容量優化配置模型的求解。與標準WOA、DE和CS算法對比，改進的鯨魚算法在求解效率、全局收斂能力以及尋找最優解方面具有優越性。

(3)算例分析中對每一個典型日1天24 h所對應的數據進行優化計算時，用時均不超過10 s；將改進的WOA應用于容量配置模型求解，進一步加快收斂速度且伴隨計算機運算能力的提升，優化計算的時間還可以進一步縮短。所以該優化策略的遠算效率可以滿足并網型微電網實時調度。