基于加權(quán)特征子空間的支持向量機核函數(shù)研究

梁禮明， 郭 凱， 盛校棋

(江西理工大學(xué)電氣工程與自動化學(xué)院， 贛州 341000)

支持向量機(support vector machine，SVM)作為機器學(xué)習(xí)的重要組成部分，它通過利用數(shù)據(jù)間的角度與距離來表示映射到高維空間的數(shù)據(jù)，避免了“維數(shù)災(zāi)難”的問題，同時它還兼?zhèn)湎∈杈仃嚨奶匦浴５撕瘮?shù)所具備的稀疏矩陣的特性較為簡單，在處理重疊子空間[1]問題時仍顯不足。當下核函數(shù)的研究主要在尋找更多適合不同特征關(guān)系的核函數(shù)，這樣的方法并沒有改變交叉空間數(shù)據(jù)點之間的關(guān)系。

文獻[2]將隨機核函數(shù)與線性核函數(shù)進行結(jié)合，研究出了線性隨機核大大提高了運算速度，同時使得核函數(shù)可以滿足訓(xùn)練樣本遠遠小于樣本量。該文還指出特征在運算中的重要性，但是并沒有對特征的權(quán)重進行研究。文獻[3-4]分別提出了模糊相似度量的核函數(shù)的構(gòu)造與孿生核函數(shù)的研究，這兩種方法只是對特征集合的描述進行了改變，只是增大或減小了每兩個數(shù)據(jù)點間關(guān)系并沒有根據(jù)數(shù)據(jù)特征的特性對數(shù)據(jù)進行優(yōu)化改變。

基于以上核函數(shù)優(yōu)化的不足，提出一種將聚類算法與分類算法結(jié)合的方法來優(yōu)化核函數(shù)。該方法引入了對特征子空間加權(quán)處理的方法，針對不同類別、不同特征的區(qū)分度，對樣本數(shù)據(jù)進行特征子空間加權(quán)處理，改變部分數(shù)據(jù)點間的關(guān)系，縮小了數(shù)據(jù)點之間的重疊空間。同時利用優(yōu)化的稀疏條件下的重疊子空間聚類算法[1]，將數(shù)據(jù)集中同類數(shù)據(jù)間隔稠密化和不同類別數(shù)據(jù)間隔稀疏化以達到提高核函數(shù)泛化能力和學(xué)習(xí)能力。該方法融合稀疏矩陣的數(shù)據(jù)稀疏化特性、子空間[5-6]的不同類別以及不同數(shù)據(jù)特征空間的規(guī)劃能力，對各種核函數(shù)的學(xué)習(xí)能力與泛化能力得到顯著提升，能夠獲得較好的分類效果。

1 理論基礎(chǔ)

1.1 核函數(shù)

核函數(shù)的構(gòu)造需要滿足Mercer定理[7]，而Mercer定理主要是通過核函數(shù)確定核矩陣的要求。

定理1(Mercer定理)要保證Frobenius范數(shù)下的對稱函數(shù)K(xi,xj)為正數(shù)ak>0，將對稱函數(shù)展開為

(1)

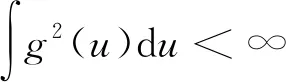
SVM在獲得分類標簽時，使用的決策函數(shù)為

(2)

式(2)中：αi、b是通過求解式(3)最優(yōu)化問題獲取的；yi表示數(shù)據(jù)xi的對應(yīng)標簽。

(3)

由式(1)可知，φ(xi)φ(xj)描述的是將低維空間映射到高維空間數(shù)據(jù)點間的表達方式，進一步可以轉(zhuǎn)化為K(xi,xj)，利用數(shù)據(jù)特征空間數(shù)據(jù)間內(nèi)積或者距離關(guān)系通過函數(shù)的關(guān)系達到能夠反映高維數(shù)據(jù)空間關(guān)系的形式。常用核函數(shù)類型有：①以距離為衡量標準的核函數(shù),如高斯核函數(shù)、二次有理核、多元二次核和逆多元二次核等；②以內(nèi)積為衡量標準的核函數(shù)，如線性核函數(shù)、多項式核函數(shù)等。

研究表明以距離為主的核函數(shù)實用性相較于以內(nèi)積為主的核函數(shù)在現(xiàn)實生活中泛化性和學(xué)習(xí)性更強[8]。以距離為主的核函數(shù)與聚類算法相似，依靠計算數(shù)據(jù)點間的距離的遠近來進行預(yù)測分類，因此將兩者結(jié)合在一起是可行的。

1.2 加權(quán)特征子空間

1.2.1 特征子空間重疊率描述

對于一組數(shù)據(jù)集每一個類別空間可以看作一個子空間，每一個數(shù)據(jù)的特征也可以看作一個特征子空間。利用超球體的思想將不同類別、不同特征的數(shù)據(jù)建立超球體模型，以最小超球體間的交叉范圍來計算空間的重疊率[9]。

超球體描述的目標函數(shù)為

(4)

式(4)中：a為球心；R為超球體半徑；C為懲罰參數(shù)；ζi為松弛變量。

利用建立的不同類別及特征超球體的球心及半徑計算相同特征下不同類別的超球體的交叉體積與公共體積。其空間重疊描述為[10]

(5)

式(5)中：Q為重疊率；L1,i為類別1在缺少特征i中所占空間；L2,i為標簽2在缺少特征i空間中所占空間；FC為L1,i與L2,i的交叉空間；FA為L1,i的空間；FB為L2,i的空間長度。式(2)與文獻[11]文本特征重要度相似，是利用特征的重疊率初步評估特征的重要程度的度量。

1.2.2 特征子空間信息熵描述

對于任意數(shù)據(jù)集(x1,x2,…,xn)T，其用每一列特征可以表示為(T1,T2,…,Tn)， 經(jīng)過對每一列特征加權(quán)可以表示為(ω1T1,ω2T2,…,ωnTn)。確定每一特征的加權(quán)系數(shù)是特征加權(quán)的重中之重，采用空間重疊率與信息熵的結(jié)合使用。

信息熵H的大小決定數(shù)據(jù)的有序程度，信息熵H的數(shù)值越接近0說明數(shù)據(jù)的有序程度越高，相反信息熵的數(shù)值越大說明數(shù)據(jù)的有序程度越低[12]，因此通過信息熵的大小判斷數(shù)據(jù)的有序程度可以進一步說明該組數(shù)據(jù)在分類中占的重要性。信息熵H的計算公式如式(6)所示：

(6)

式(6)中：pi為數(shù)據(jù)(x1,x2,…,xn)T的輸出概率函數(shù)。

1.2.3 特征子空間加權(quán)

對數(shù)據(jù)集的樣本特征Ti設(shè)置權(quán)值：

(7)

最后，對所有所有的特征子空間權(quán)值歸一化，即

(8)

1.3 加權(quán)混合范數(shù)的距離空間模型

1.3.1 距離模型

數(shù)據(jù)點間距離的表達方式來作為衡量分類的一類重要標準，在分類實驗中常用的是明可夫斯基距離(Minkowski distance)[13]。設(shè)數(shù)據(jù)點P(x1,x2,…,xn)T和Q(y1,y2,…,yn)T∈Rn那么，明可夫斯基距離可以表示為

(9)

式(9)中：d為數(shù)據(jù)點P、Q間的明科夫斯基距離。

在傳統(tǒng)的核函數(shù)中對數(shù)據(jù)點間的描述主要以Frobenius范數(shù)與數(shù)據(jù)點間的內(nèi)積為主，結(jié)合SVM與稀疏矩陣的思想，提出一種混合范數(shù)的特征子空間模型，目的是在保障類間間距稀疏性的同時增加類內(nèi)間距的緊密性。對于一個訓(xùn)練樣本數(shù)據(jù)，其中包含N個特征，M個數(shù)據(jù)點，利用核函數(shù)在表示數(shù)據(jù)點之間的關(guān)系時組成一個M×M矩陣，該矩陣為一個對稱矩陣同時也是個正定矩陣。引入L1范數(shù)來增加矩陣間的稀疏性，具體距離表示模型可表示為

(10)

1.3.2 加權(quán)方式

在處理數(shù)據(jù)問題時，由于數(shù)據(jù)的復(fù)雜多樣化的問題，只是引入L1正則化來保障核矩陣的稀疏性其效果并不是很理想。文獻[14-15]提出對L1正則化加權(quán)的方法，通過迭代更新的方法對L1范數(shù)進行改變，并且通過大量實驗證明了該方法優(yōu)于單獨使用L1范數(shù)的效果，能夠得到更具有稀疏性的核矩陣，使得L1更逼近L0。通過式(11)進行求解[16]:

(11)

式(11)中：δ為控制參數(shù)；A為由已知數(shù)據(jù)求向量平均值確定的向量矩陣；c為給定的限制參數(shù)。

其加權(quán)方式為

(12)

式(10)可以表示為

(13)

2 實驗仿真與分析

支持向量機核函數(shù)分類算法流程如圖1所示。實驗仿真數(shù)據(jù)均來自UCI(UC Irvine machine learning repository)數(shù)據(jù)庫，并且每組數(shù)據(jù)均帶標簽。SVM分類器應(yīng)用Lib-SVM工具箱，仿真環(huán)境運用MATLAB R2018a，運行于Intel (R) Core (TM) i5-7200U/2.50 GHz、8 GB內(nèi)存的計算機。實驗隨機選取每組樣本的80%為訓(xùn)練樣本，其余20%為測試樣本。

圖1 支持向量機核函數(shù)分類流程圖Fig.1 Support vector machine kernel function classification flow chart

2.1 建立加權(quán)特征子空間

在UCI數(shù)據(jù)庫中隨機抽取一組數(shù)據(jù)實驗，該數(shù)據(jù)為User Knowledge Modeling Data Set，即學(xué)生對直流電機的知識水平數(shù)據(jù)集，數(shù)據(jù)集STG表示目標對象素材的學(xué)習(xí)時間輸入值，SCG表示目標對象用戶重復(fù)次數(shù)輸入值，STR表示與目標對象相關(guān)的用戶學(xué)習(xí)時間輸入值，LPR表示與目標對象相關(guān)的用戶考試成績輸入值，PEG表示用戶對目標對象的考試成績輸入值，UNS表示用戶知識水平目標值。

首先對樣本數(shù)據(jù)進行歸一化處理，使得各個數(shù)據(jù)點的各特征值小于1，并保證各特征間的相對關(guān)系；然后利用式(4)、式(5)對各特征進行重疊空間描述；再根據(jù)式(6)～式(8)與各特征重疊空間的關(guān)系對樣本數(shù)據(jù)進行加權(quán)處理；最后通過對實驗數(shù)據(jù)進行分析建立加權(quán)特征子空間的必要性與可行性，具體的實驗內(nèi)容及數(shù)據(jù)如表1所示。

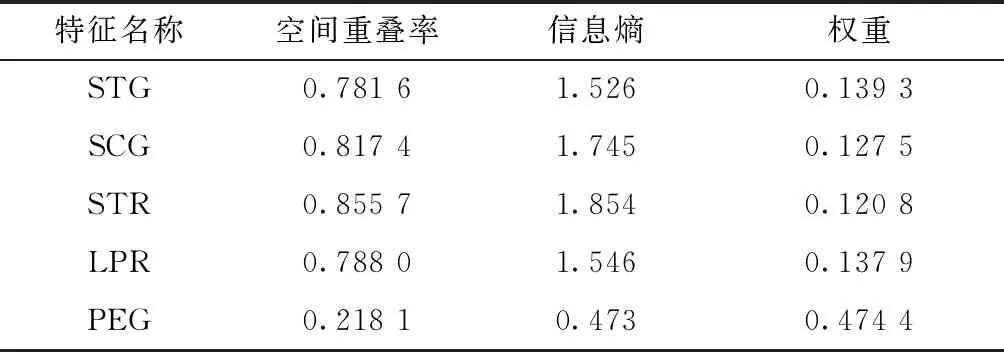
表1 數(shù)據(jù)集各特征空間的重疊率、方差和加權(quán)比例Table 1 Overlap rate, variance and weighted ratio of each feature space of the data set

從表1可知，無論是信息熵還是空間重疊率特征PEG的數(shù)值最低，即特征PEG在數(shù)據(jù)分類的過程起到了比較重要的作用。

2.2 距離矩陣的建立與仿真測試

該實驗以評估對稱距離矩陣內(nèi)的重復(fù)率進行評估對核函數(shù)的影響。通過引入L1范數(shù)減少了矩陣內(nèi)部元素的重復(fù)率，同時增加數(shù)據(jù)點間的距離，進一步增加了核矩陣的稀疏性，使得大部分數(shù)據(jù)更接近0，增大了數(shù)據(jù)間的區(qū)分度。在UCI中隨機抽取四組數(shù)據(jù)進行實驗分析。各數(shù)據(jù)集分類結(jié)果對比如表2所示。

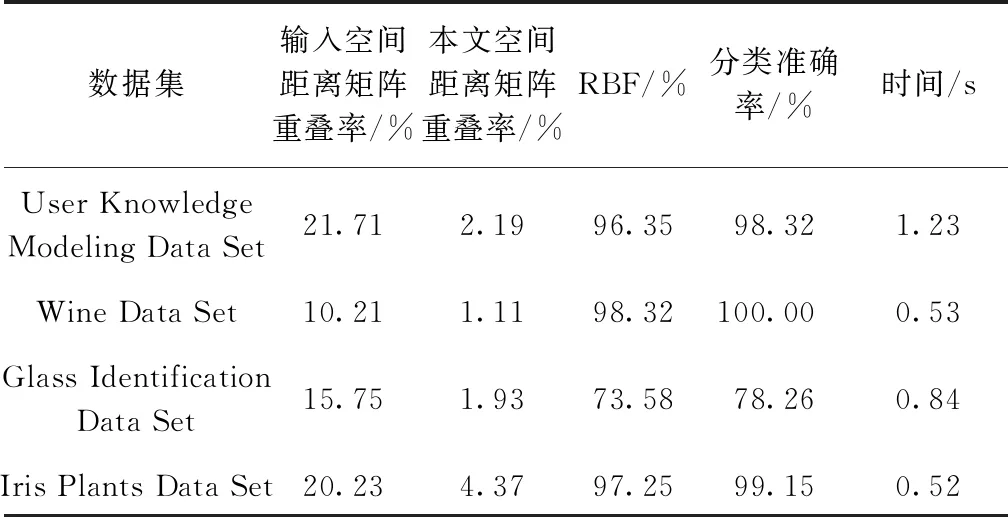
表2 各數(shù)據(jù)集分類結(jié)果對比Table 2 Comparison of classification results of each data set

通過實驗仿真可知，對于核函數(shù)中引入L1范數(shù)可以減少距離數(shù)據(jù)的重復(fù)率，同時可以增加類內(nèi)間距的緊密型和類間間距的稀疏性，以達到更好的泛化效果。為了更好地闡釋核函數(shù)通過引入L1范數(shù)能夠更好地增強核函數(shù)的泛化性，通過對部分以距離為衡量標準的核函數(shù)進行研究，同時對引入L1范數(shù)的輸入距離矩陣進行分析，來說明該方法的可行性與有效性。

從圖2分析可知，以距離為主要評判方式的核函數(shù)(如高斯核函數(shù)、二次有理核核函數(shù)和逆多元二次核函數(shù)等)，隨著距離的增加該距離所對應(yīng)的核矩陣的數(shù)值越接近0。

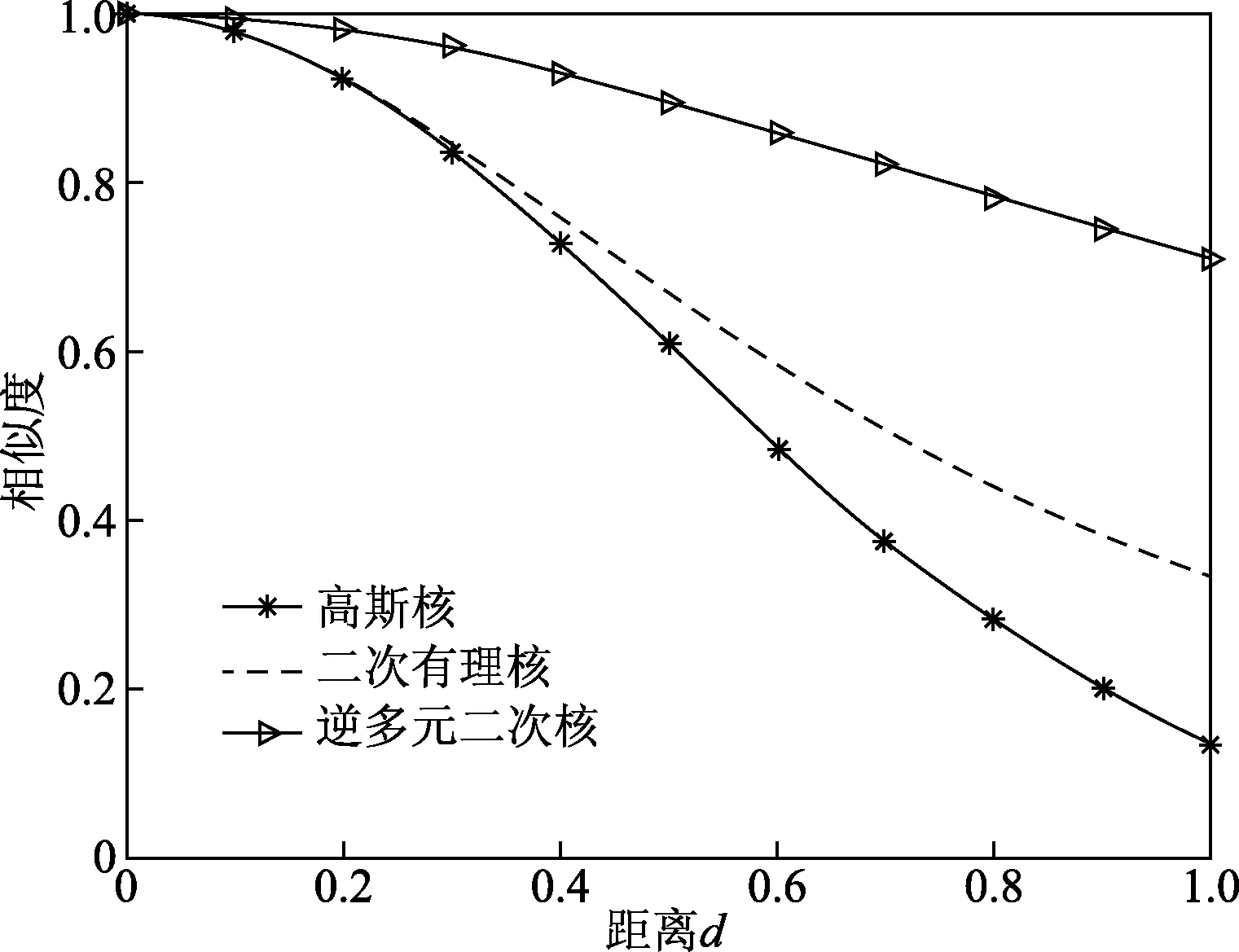
圖2 核函數(shù)特性比較Fig.2 Kernel property comparison

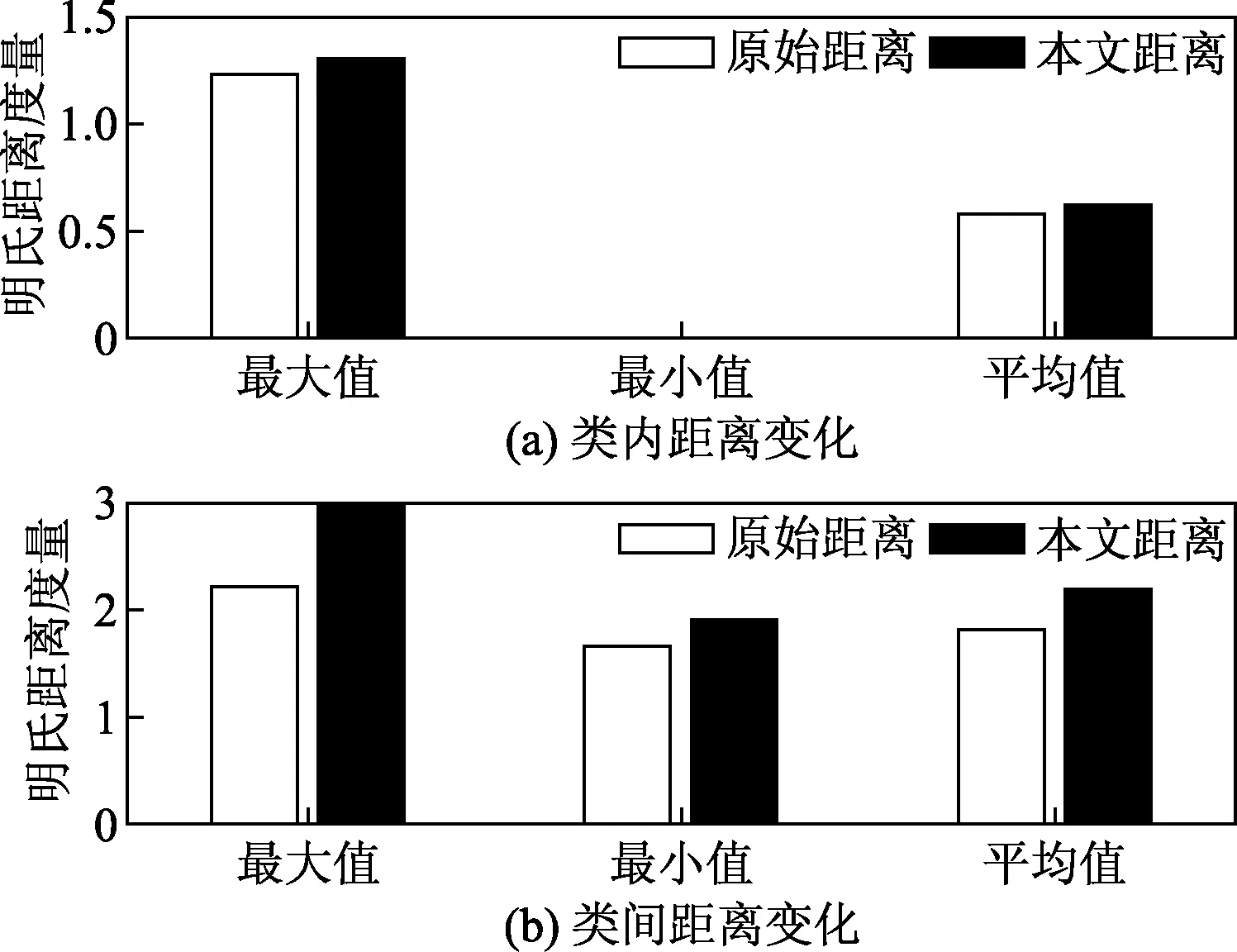
圖3 引入L1范數(shù)距離變化Fig.3 Introducing L1 norm distance variation

圖3(a)、圖3(b)分別為同一數(shù)據(jù)集同類標簽類內(nèi)特征距離和不同類標簽特征距離經(jīng)過引入L1范數(shù)距離變化的情況分析圖。由圖3可知，通過引入L1范數(shù)使得類內(nèi)、類間距離均得到提高，但是類內(nèi)間距提升的幅度較小，而類間間距變化較大。所以通過引入L1范數(shù)能夠有效地提升數(shù)據(jù)類內(nèi)緊密型和類間稀疏性的特點。再與以距離為分類手段的核函數(shù)，該類核函數(shù)可以通過增大距離的方式來達到核矩陣稀疏化的目的，進而達到拉大同類數(shù)據(jù)與異類數(shù)據(jù)的距離關(guān)系，從而可以提高核函數(shù)的學(xué)習(xí)能力與泛化能力。

2.3 樣本數(shù)據(jù)對比分析

隨機選取文獻[5，17]中所用的數(shù)據(jù)集進行對比試驗，數(shù)據(jù)集包括：Breast Cancer Wisconsin、Fisheriris Data Set、Wine Data Set、Heart Disease Data Set、Indian Liver Patient Data Set、Australian Credit Approval Data Set六組，對六組數(shù)據(jù)分別進行特征子空間的加權(quán)處理與引入L1范數(shù)的稀疏化處理。分類結(jié)果采用5次實驗取平均值的方式與文獻[5,17]的分類結(jié)果進行對比，結(jié)果如表3所示。

通過與其他文獻的分類效果以及利用經(jīng)過優(yōu)化與非優(yōu)化的二次有理核的分類結(jié)果對比分析。從核函數(shù)的角度分析，RBF核函數(shù)相對于二次有理核函數(shù)有較大的優(yōu)勢，如何選擇正確的核函數(shù)對實驗的結(jié)果起到一定作用；從核函數(shù)內(nèi)部間分析，經(jīng)過本文算法優(yōu)化過的核函數(shù)能夠顯著地提高核函數(shù)的分類效果，無論是在RBF核函數(shù)間的對比，還是在二次有理核函數(shù)間的對比，本文算法在一定程度上提高了核函數(shù)的分類準確率。從理論上分析，對一組數(shù)據(jù)中的各個特征進行了挖掘，利用科學(xué)的手段對不同特征對分類結(jié)果的影響進行了分析，更進一步使得核函數(shù)挖掘出數(shù)據(jù)潛在的信息，進而提高分類準確率。同時，還引入了L1范數(shù)，使得同類數(shù)據(jù)間更加緊密，異類數(shù)據(jù)間更加稀疏，增大了數(shù)據(jù)間的可區(qū)分性，進而提高了分類效果，增強了核函數(shù)的學(xué)習(xí)能力與泛化能力。

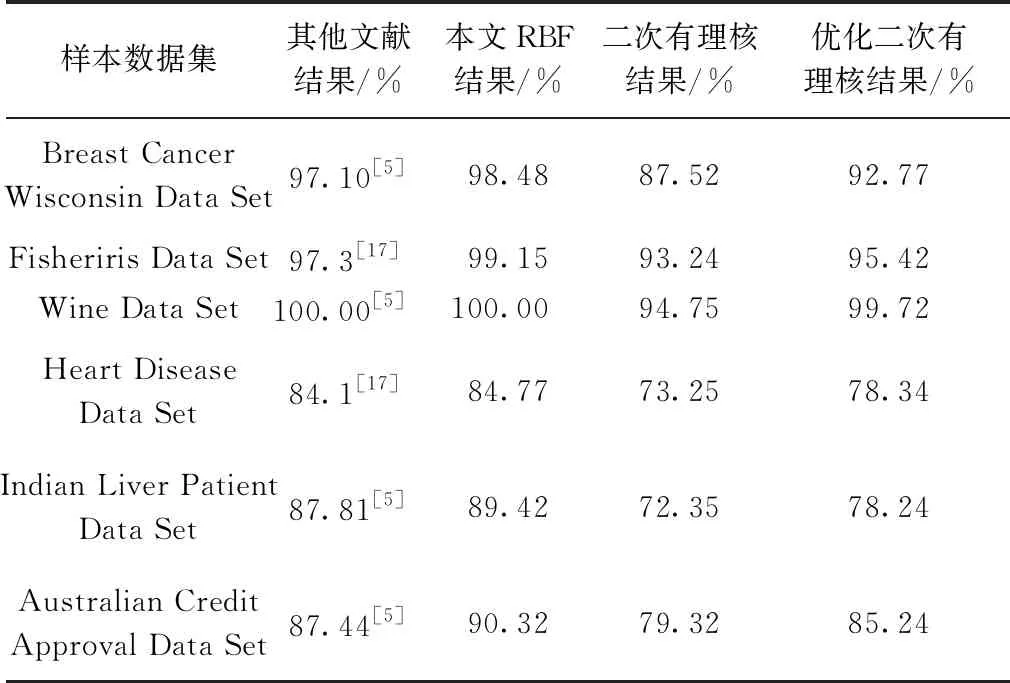
表3 本文算法與其他文獻分類效果對比Table 3 Comparison of the classification effect between the proposed algorithm and other documents

3 結(jié)論

利用特征子空間加權(quán)的方式，較好地解決了特征對分類決策的影響不明確的問題，使得核函數(shù)能夠更好地挖掘數(shù)據(jù)集一些潛在的關(guān)系。為充分發(fā)揮數(shù)據(jù)本身的價值屬性，針對一些以距離為主要衡量標準的核函數(shù)進行的優(yōu)化與改進，通過引入L1范數(shù)使得數(shù)據(jù)輸入空間距離得到一定程度的擴大。同時由于類內(nèi)間距與類間間距不同的變化效果達到稀疏化核矩陣的目的，使得類內(nèi)間距與類間間距的重合率更小，同時類間部分核矩陣數(shù)值更接近0。通過仿真實驗證明該方法的可行性和有效性。本文算法融合核函數(shù)、稀疏矩陣與特征加權(quán)等有效地提升核函數(shù)的學(xué)習(xí)能力與泛化能力，但是在一些數(shù)據(jù)集中仍存在不小的交叉空間距離，這樣的交叉空間是優(yōu)化核函數(shù)的主要矛盾之一，故下一步主要研究如何減少距離空間的重疊率。