LNG儲罐內罐小孔泄漏工況下溫度場數值模擬

張 娜 李兆慈 郭志超

中國石油大學(北京)油氣管道輸送安全國家工程實驗室/城市油氣輸配技術北京市重點實驗室, 北京 102200

0 前言

在LNG產業鏈中,儲存是重要的一環。天然氣低溫液化后經遠洋運輸到達世界各地LNG接收站,接收站既是海上LNG運輸的終點也是陸上天然氣供應的起點[1]。儲罐是接收站內最重要的儲存設備,它的安全至關重要。接收站的儲罐體積龐大,結構復雜,內罐工作在-162 ℃左右的低溫環境,因此儲罐在安全運行方面存在諸多需要注意的問題[2]。隨著LNG儲存設施大型化趨勢和高安全性的要求,全容罐因為具有更高的安全性得到了廣泛應用[3]。LNG儲罐作為接收站最核心的建筑物,是重大危險源,一旦發生事故將會造成巨大損失。當儲罐因為人為操作不當、設備損壞、管道破裂等問題發生LNG泄漏時,由于LNG是-162 ℃的深冷液體,泄漏出來的低溫液體會對設備造成低溫沖擊,危害儲罐結構的安全[4]。如LNG泄漏于地面時,會迅速從地面、周圍環境吸收熱量,蒸發為氣體。LNG全容罐分內罐和外罐,在設計和建造上能容納所儲存的低溫液體以及液體蒸發后產生的低溫氣體。由于LNG接收站一般位于沿海地帶,可能發生地震等自然災害,增加了LNG儲罐內罐泄漏的風險。所以采用合理的方法對LNG儲罐內罐泄漏進行模擬研究,對于外罐壁厚的設置、制定發生泄漏時采取的應急措施都具有重要意義。

1 LNG儲罐泄漏研究方法

因低溫導致設備材料斷裂,從而引起的儲罐泄漏,一般可根據泄漏口面積大小和泄漏處高度等因素分成兩類[5]:一類是大面積泄漏,在較短時間內儲液大量漏出,瞬間產生大量BOG氣體,可能在儲罐內形成瞬間高壓發生爆炸[6];另一類是有限孔泄漏,儲存的液體沿小泄漏口緩慢流入絕熱層,破壞絕熱層結構,對儲罐的正常運行造成影響。內罐小孔泄漏是目前最易發生的泄漏工況,本文主要針對LNG內罐小孔泄漏工況進行計算模擬。

對于LNG儲罐泄漏問題,早期通過現場模擬實驗,在野外搭建與真實事故完全一致的場景,重現當時的后果影響,得到最真實的數據資料。但這種現場試驗隨機性很大,且需花費大量人力物力,得到的結果僅對某一特定的事故有幫助,但對類似事故參考意義不大,因此需要更簡單的具有普適性的方法[7]。通過物理模型構建類似實際情況,可在實驗室完成的小型泄漏模擬實驗來研究實際LNG泄漏擴散規律。研究LNG泄漏擴散過程的物理模擬一般采用風洞試驗[8]。20世紀70、80年代,MeroneyR N[9]已經模擬出LNG高空和地面釋放情況下的LNG擴散。

數值模擬是應用比較普遍的一種借助計算機完成的LNG儲罐泄漏擴散模擬方法。這種方法無需設置實驗,可借助不同的數學模型完成,經濟省時,可以得到詳盡的結果。隨著計算機計算能力的不斷提高,加上有限容積法、有限元分析法等數值計算方法的發展,基于數值計算的計算流體力學(CFD)方法得到了蓬勃發展[10]。

LNG泄漏后的擴散過程可通過速度、濃度和溫度進行描述,其控制方程包括連續性方程、動量方程、能量方程、擴散方程、湍流動能方程、湍流動能耗散方程[11]等。

現場實驗會耗費較大的人力、物力和財力,同時外界的環境變化復雜,在某些情況下難以獲取理想的數據。風洞實驗在低風速和低雷諾數條件下進行比較困難[11]。幾種方法互有長短,實際研究中可綜合運用,但鑒于數值模擬的耗時短、成本低以及高度可重復性,近幾年成為此類研究中最廣泛使用的方法[12]。

對比LNG泄漏擴散的各種研究方法可知,CFD模擬具有較好的適用性,但要準確模擬LNG泄漏擴散過程,對初始條件、邊界條件設置要求較高[13]。同時CFD模擬還存在一些問題需要解決,如過分簡化處理源項和地面傳熱方式,對于關鍵影響因素的敏感性分析不足等。

2 內罐泄漏溫度場計算模擬

隨著內罐小孔泄漏的持續,內罐受影響區域逐漸向保溫層外側和底部發展,危及LNG外罐的安全。

在LNG儲罐內罐發生泄漏時,LNG會沿有限孔緩慢流出,再沿著儲罐內壁外的彈性玻璃纖維氈流入環形空間的絕熱層中。絕熱層由彈性氈、膨脹珍珠巖和泡沫玻璃磚組合而成[14]。以 20 000 m3雙金屬全容式LNG儲罐為例,內罐高度30 m,內罐罐徑(直徑)30 m,外罐罐壁高度31 m,外罐罐徑(直徑)32.378 m，外罐拱頂高度4.66 m。內罐由底板、頂板及10層壁板組成,外罐由底板、頂板、10層壁板及梯子欄桿組成。

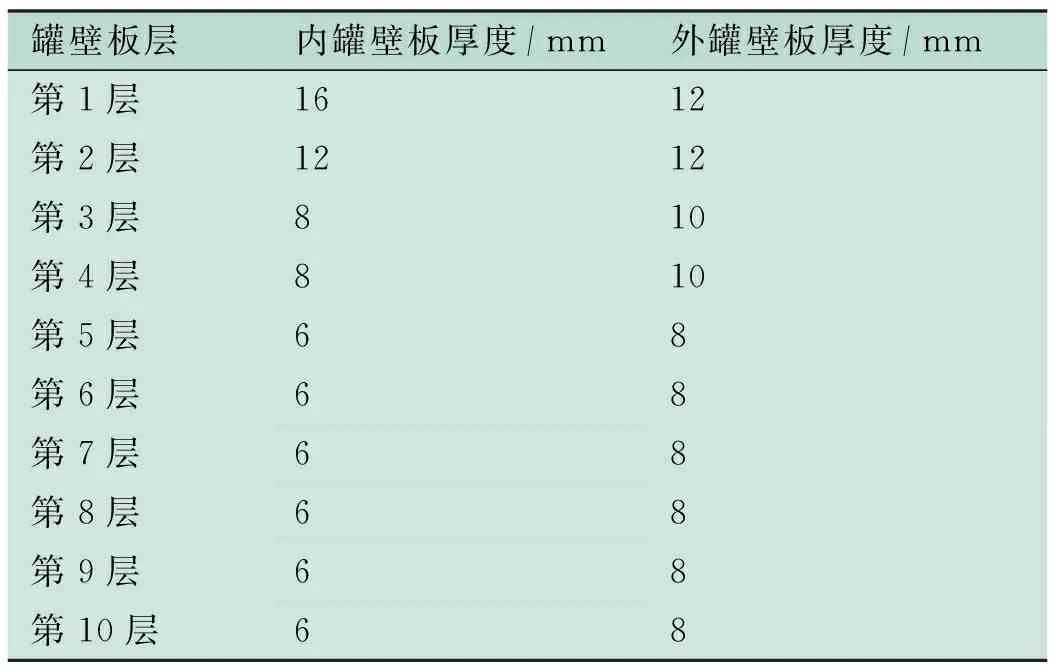
由于內罐整體高度為30 m,所以每層壁板高度為3 m。內、外罐壁每層壁板厚度見表1。

表1 內、外罐各層壁板厚度表

Tab.1 Thickness of each layer of the tank innerwall and outerwall

罐壁板層內罐壁板厚度/mm外罐壁板厚度/mm第1層1612第2層1212第3層810第4層810第5層68第6層68第7層68第8層68第9層68第10層68

儲罐絕熱層結構見圖1，內壁絕熱材料的厚度及導熱系數等參數見表2。

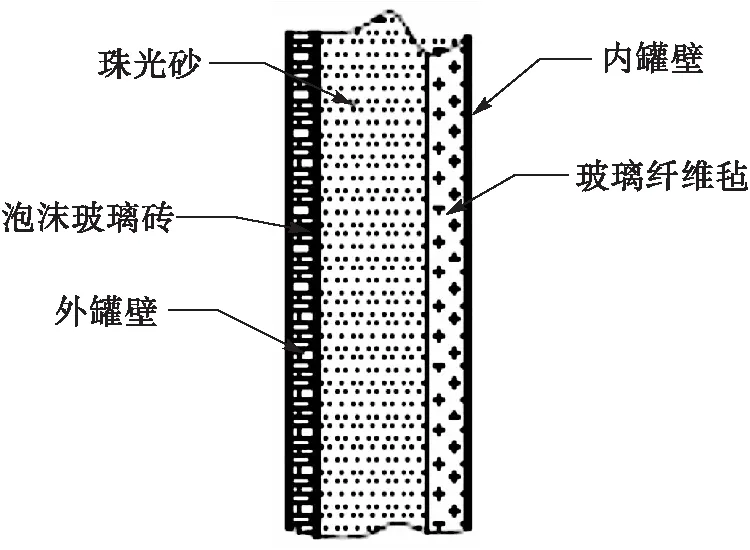
圖1 罐壁絕熱層結構示意圖Fig.1 The wall insulation of the tank

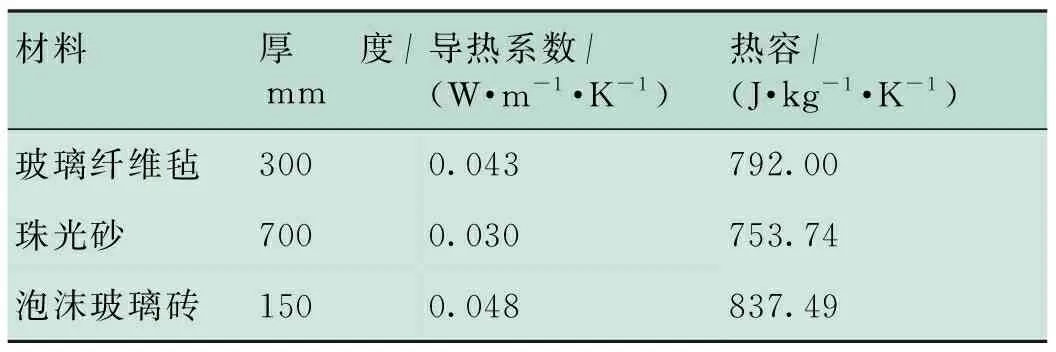
表2 儲罐罐壁絕熱層數據表

Tab.2 Wall insulation of the tank

材料厚度/mm導熱系數/(W·m-1 ·K-1)熱容/(J·kg-1 ·K-1)玻璃纖維氈3000.043792.00珠光砂7000.030753.74泡沫玻璃磚1500.048837.49

絕熱材料是由氣相與固相構成的多孔性組織,固體材料內部存在互相連通的氣相空間,這給LNG泄漏提供了一條滲流通道,因此LNG儲罐內罐泄漏模擬可采用多孔介質模型[15]。

在內罐泄漏條件下,對儲罐的溫度邊界條件作以下假設:外罐壁初始溫度取正常操作條件下的環境溫度20°C,外罐壁與空氣的對流換熱系數取25 W/(m2·K)；儲罐內LNG溫度為-162°C,內罐溫度與儲液溫度相同。不考慮LNG泄漏時的相變，外罐壁和罐底部絕熱層的下部均為絕熱壁面,外罐壁頂部也設為絕熱壁面。由此得到穩態時罐壁絕熱層的溫度分布,見圖2。

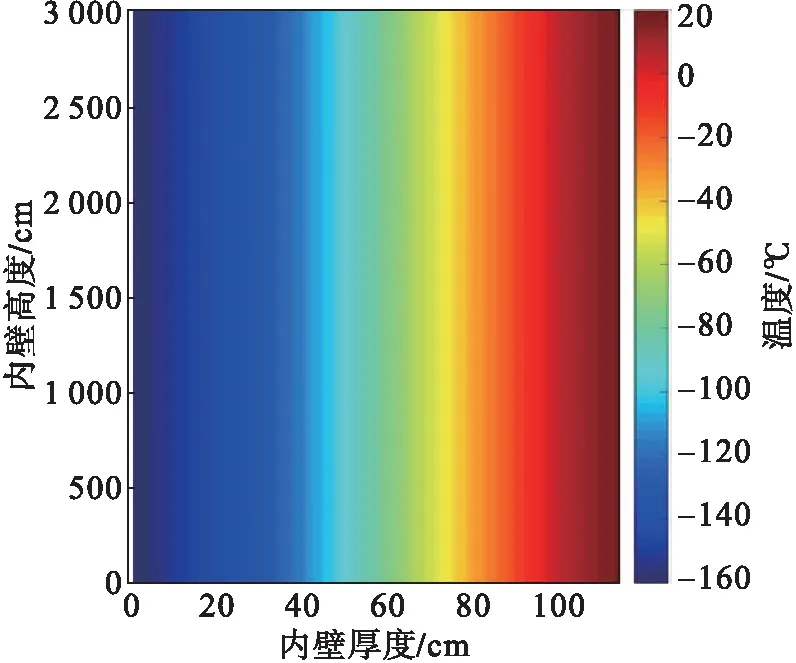
圖2 穩態溫度分布圖Fig.2 Temperature distribution in steady state

儲罐壁高30 m,故i的取值范圍在0～3 000,在距離罐底10 m(i=1 000)處設置泄漏工況,泄漏孔徑為10 mm,泄漏點流速為0.02 m/s。

考慮泄漏點處對流換熱,設置泄漏點(i=1 000)處溫度為LNG的溫度,與上下邊界進行對流換熱,由傅立葉定律和牛頓冷卻公式可知其熱流量相等,即：

(1)

式中:h為對流換熱系數,W/(m2·K);Tw為壁面溫度,℃;Tf為流體溫度,℃;T為絕熱層溫度，℃;λ為介質導熱系數,W/(m·K)；Y為內壁高度方向。

其中,對流換熱系數h是一個與流體密度、比熱容、流速、黏度、導熱系數有關的復雜函數,h=f(ρ,cp,λ,u,l,μ),可通過計算雷諾數Ref、努賽爾數Nuf和普朗特數Prf得到[16],具體計算按式(2)。

(2)

式中:u為流體流速,m/s;l為當量長度,m;μ為流體黏度,m2/s。對于非圓形截面的槽道,l取當量直徑作為特征長度de。

(3)

式中:Ac為槽道的流動截面積,m2;P為潤濕周長,即槽道壁與流體接觸面的長度,m。

再計算普朗特數:

(4)

式中:Cp為流體比熱容,J/(kg·K);a為流體導熱系數,W/(m·K)。

最后再由努賽爾數求得流體的對流換熱系數h:

(5)

將內罐泄漏后的罐壁傳熱簡化成二維非穩態對流換熱問題,先求得泄漏流體在罐壁內的流場分布。對彈性多孔介質單相不可壓縮流體不穩定滲流問題,其運動方程為:

(6)

式中:ν為流體泄漏速度,m/s;K為介質滲透率,μm2。

對于二維平面:

(7)

對于彈性孔隙介質，其狀態方程(多孔介質和液體都是可壓縮的):

φ=φa+Cf(p-pa)

(8)

式中:φ為孔隙介質度；Cf為流體的壓縮系數；φa為標準大氣壓下孔隙介質度；pa為標準大氣壓，Pa;p為流體壓力，Pa。

對于彈性液體:

ρ=ρaeCL(p-pa)=ρa[1+CL(p-pa)]

(9)

式中:ρ為液體密度,kg/m3;ρa為標準大氣壓下液體密度,kg/m3;CL為液體彈性壓縮系數。

單相流體的連續性方程為:

(10)

將運動方程和狀態方程代入連續性方程可得:

(11)

通過對設置的儲罐內壁絕熱層進行網格劃分,確定出邊界點、角點和內點,再對二維非穩態滲流壓力方程進行離散,最后采用TDMA算法加快迭代計算速度,由此計算模擬可得到LNG泄漏至內罐壁的流場分布,其橫坐標為內壁厚度,縱坐標為內壁高度,罐底至泄漏點即i=1 000下方的壓力分布見圖3。

由圖3可知,在計算步長內,其壓力在泄漏點處最大,逐漸向下削弱。通過對x和y方向上的壓力求偏導,可計算得到二維速度場的分布,圖4為罐壁泄漏點(i=1 000)下方二維速度分布矢量圖。

由模擬結果可以看出,由于罐壁絕熱層材料物理特性不同,其滲透擴散速率也不同。將模擬計算得到的流場分布與溫度結合,將模擬計算得到的速度分布作為對流擴散項添加到二維非穩態對流換熱方程中,即完成流場溫度場的耦合。

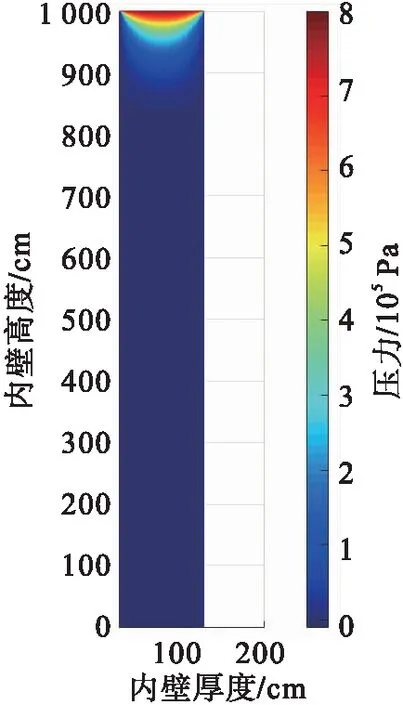
圖3 泄漏點下方壓力分布圖Fig.3 Pressure distribution below the leak point

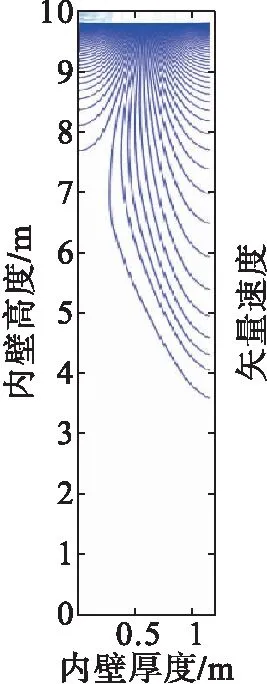
圖4 速度分布矢量圖Fig.4 Speed distribution vetor

(12)

對式(12)進行離散,采用中心差分形式,對角點、邊界點和內點分開離散,再用Gauss-Seidel迭代法計算內壁絕熱層區域內的內點,得到LNG液體泄漏后在罐壁內的溫度分布(泄漏點i=1 000)。

由圖5的溫度分布云圖可知,隨著計算時間的推進,泄漏液體向下擴散程度大,且越靠近泄漏點處泄漏速度越大,溫度變化梯度也隨之增大。

3 Fluent軟件模擬驗證

Fluent軟件是采用有限容積法對控制方程進行離散并求解的,離散方程有清晰的物理解釋,其內置各類模型及方法可用于求解不同流體力學問題,針對滲流問題,亦采用多孔介質模型進行模擬。

Fluent軟件中涉及到傳熱問題時,其基本守恒方程為質量守恒、動量守恒以及能量守恒方程[17]。多孔介質模型本質上其實僅在動量方程上附加源項;若涉及傳熱問題,可以只修改能量方程的傳導通量及瞬態項[17]。實際上,Fluent軟件并不存在獨立的多孔介質區域,模型假設多孔介質固體區域為流體區域,對流入其中的流體設置阻力系數以達到滲流效果[18];如涉及熱傳導,設置多孔區域孔隙率,通過孔隙率換算出有效熱導率,將其添加于能量方程中以達到熱量傳遞效果[19]。計算得出絕熱材料的阻力系數見表3。

使用ANSYS workbench工作平臺建立二維模型,合理劃分網格后,將參數條件導入Fluent軟件中進行模擬,在上述相同的溫度邊界條件下,通過穩態求解的方法得到罐壁的溫度場分布，見圖6。

a)100時步a)100 time steps

b)500時步b)500 time steps

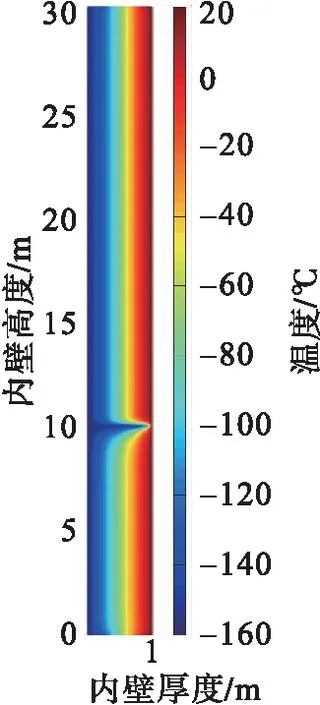
c) 1 000 時步c)1 000 time steps

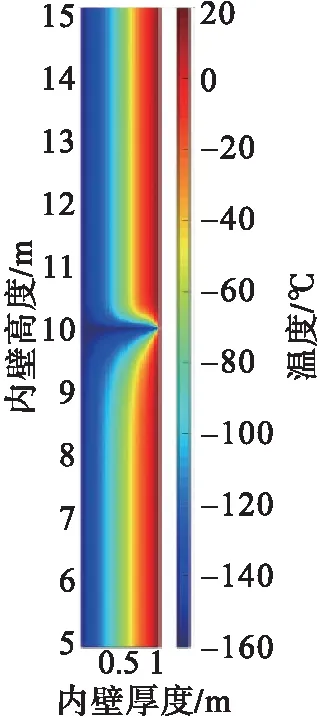
d) 1 000 時步放大d)1 000 time steps amplification

表3 多孔介質模型各絕熱材料參數表

Tab.3 Insulation materials parameters in porous model

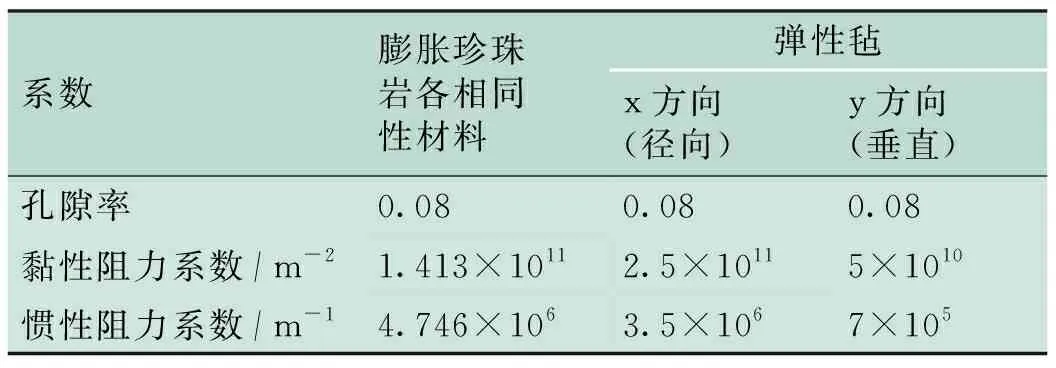
系數膨脹珍珠巖各相同性材料彈性氈x方向(徑向)y方向(垂直)孔隙率0.080.080.08黏性阻力系數/m-21.413×10112.5×10115×1010慣性阻力系數/m-14.746×1063.5×1067×105

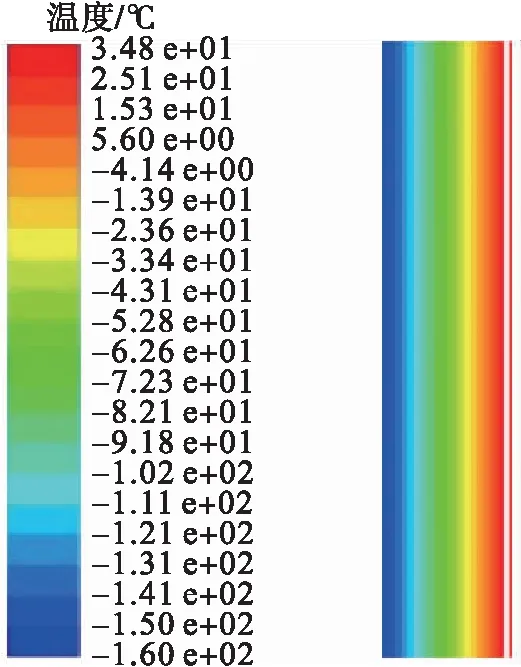
圖6 罐體穩態溫度分布圖Fig.6 Temperature distribution of the tank in steady state

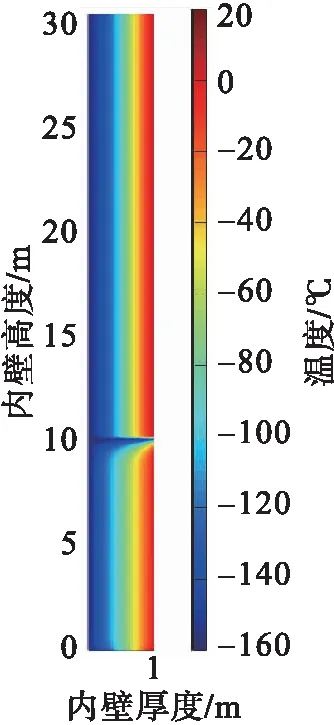
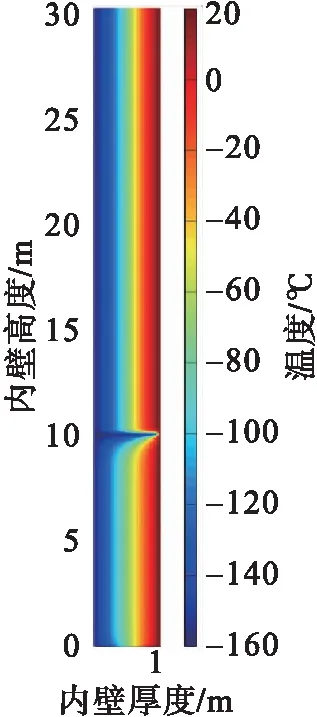
再模擬泄漏工況,泄漏點為距儲罐底部10 m處,泄漏孔直徑10 mm,泄漏熱溫度條件與上述一致。LNG從泄漏口流出,采用多孔介質模型,按表3設置模擬參數,獲得不同時刻罐體溫度分布,結果見圖7。

圖7 LNG儲罐泄漏工況下溫度分布圖Fig.7 Temperature distribution diagram of LNG tank under leakage conditions

由圖7可以看出,內罐泄漏時,漏液先向下聚集,靠近內罐壁的彈性氈快速降溫至LNG溫度,當低溫液體到達罐底時,低溫LNG液體富集底部,而后沿罐底逐漸滲透到膨脹珍珠巖中,最后擴散到整個絕熱層。經計算,泄漏后約26 h低溫液體滲透至全部絕熱層中。

4 結論

通過Fluent軟件模型和CFD計算得到了相似的結果,在計算時長和邊界條件的設置難度上,Fluent模型要優于CFD直接計算,所以如果有模型符合應用場景時,可以選取模型進行計算。

LNG內罐發生泄漏時,漏液先向下聚集,呈不對稱分布,溫度分布表現為靠近泄漏源處的彈性氈首先降溫到LNG溫度,且此處的溫度梯度較大;而后沿罐底逐漸滲透到膨脹珍珠巖中,隨著泄漏時間的不斷推進,漏液最后擴散至整個內壁絕熱層。但由于次容器與泡沫玻璃磚的存在,外罐壁的溫度與外界溫度相差不到1 ℃,起到了良好的絕熱保冷效果。