X 舵潛艇空間旋回運動控制系統設計

夏極，黃斌

1 海軍裝備部駐武漢地區第二軍事代表室，湖北武漢430064

2 海軍工程大學動力工程學院，湖北武漢430033

0 引 言

采用X 舵的潛艇，每個舵葉旋轉都會同時影響潛艇的深度、縱傾、橫傾和航向［1-2］。與十字舵相比，X 舵的操縱性更靈活，能夠實現給定姿態的空間旋回機動，但也增加了操縱方法的復雜度。國內外學者在潛艇X 舵的控制方面研究較多，內容涵蓋X 舵的優化布局［3］、安全操縱［4］、空間運動模型［5］等領域，但在潛艇X 舵的自動控制方法方面研究較少，X 舵在潛艇運動控制上的優勢還有待深入研究。本文將通過建立某型潛艇的空間運動模型，分析X 舵的控制特點，采用智能模糊控制方法實現潛艇空間旋回運動控制，為潛艇的操縱控制方法提供理論參考。

1 X 舵潛艇運動模型

X 舵的4 片舵葉正交布置，每片舵葉均能獨立偏轉；舵軸中心與潛艇中線面的夾角為45°，葉片轉動引起潛艇的偏轉和潛浮。X 舵的布局如圖1所示。圖1 中，δ1～δ4分別為X 舵4 片舵葉的舵角。

潛艇在水中的運動可看作剛體在流體中的空間運動，包括6 個運動自由度，分別為沿艇體運動坐標系x，y，z 方向的平動和轉動。文獻［1］給出了十字舵潛艇水下六自由度運動方程，若要建立X 舵潛艇的六自由度運動方程，只需要將方程中對應的舵角系數進行變換即可。定義X 舵施加給潛艇的操縱力為［6-7］

式中：X，Y，Z 分別為施加于潛艇的縱向、橫向和垂向作用力；K，M，N 分別為施加于潛艇的縱向、橫向和垂向作用力矩。式（1）中各力和力矩的表達式為

式中：Xδiδi，Yδi，Zδi，Kδi，Mδi，Nδi為操舵引起的流體水動力系數，數值由拖曳水池實驗得到；u為航速在運動坐標系x軸方向的分量；δi為X 舵的4 個舵角。將式（1）與操縱性方程［1］中艉舵和方向舵對應的力和力矩替換為X 舵操縱力和力矩，并考慮操舵角與其他運動參數的耦合等因素，可得到X 舵潛艇六自由度運動模型，具體替換過程如表1所示。表中δs，δr分別為艉舵和方向舵舵角，X舵的水動力系數Xδsδs，Xδrδr，Yδr，Zδs，Kδr，Mδs，Nδr值由拖曳水池試驗得到。

表1 六自由度運動方程中X 舵與十字舵方程的替換項Table 1 Replacement items between X-rudder and Cross-rudder of 6-DOF

本文利用基于對話框的微軟基礎類庫（microsoft foundation class，MFC）程序框架編制X舵潛艇六自由度運動仿真軟件，采用三階龍格—庫塔法求解潛艇六自由度運動微分方程，得到潛艇的運動狀態。

2 X 舵空間旋回運動分析

旋回運動是潛艇水下機動的常見方式，對于常規十字舵潛艇來說，需要同時操縱方向舵和艏、艉升降舵，來實現水下定深或空間旋回。操縱過程為：方向舵角（δr）提供旋回的誘導力，一般在旋回過程中保持舵角不變；艏舵角（δb）控制潛艇深度；艉舵角（δs）控制潛艇的縱傾。因橫傾無法由操舵進行直接控制，因此常規的十字型艉舵潛艇在旋回時都存在一定的橫傾。如前所述，X 舵每片舵葉的轉動可以同時影響潛艇的深度、縱傾、橫傾和航向，因此X 舵除了能控制縱傾和深度，還能控制橫傾，理論上為實現給定姿態空間旋回創造了條件。

首先，對單舵無控制時潛艇的空間旋回運動進行分析。潛艇航速8 kn，在無控制條件下，δ1～δ4單舵滿舵30°空間旋回相關狀態參數如表2 所示。

表2 X 舵空間旋回狀態參數Table 2 Status parameters of space turning of X-rudder

由表2 可見，采用δ1和δ4進行旋回控制時，橫傾角很小，旋回直徑較大；而采用δ2和δ3進行旋回控制時，橫傾角較大，旋回直徑較小。在δ1～δ4這4種旋回控制方式下，縱傾角和深度速率的變化幅度較小。

采用δ1和δ4進行旋回控制時，如圖2（a）所示，潛艇在Fx作用下會右旋回運動，使得艇體產生右橫傾［1］（內側傾斜），而δ1和δ4本身所受的作用力F又會使艇體左傾，可見采用δ1和δ4進行旋回控制時，δ1和δ4本身的受力會對橫傾有抑制作用。而采用δ2和δ3進行旋回時，如圖2（b）所示，潛艇在Fx的作用下會右旋回運動，使艇體產生右橫傾［1］，而δ2和δ3本身所受的作用力F 也會使得艇體右傾，可見采用δ2和δ3進行旋回時，δ2和δ3本身的受力會對橫傾有促成作用。從另一角度來看，δ2和δ3對橫傾有相對更好的控制作用。

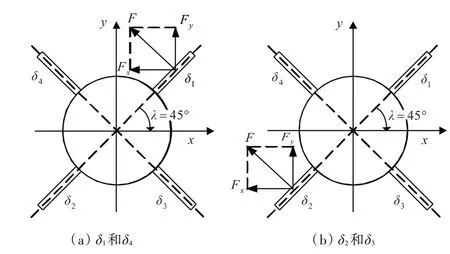
圖2 X 舵旋回運動受力分析Fig.2 Force analysis of turning motion of X-rudder

在100 s 仿真時刻，分別給X 舵4 個舵角一個30°的階躍操舵信號，橫傾角和縱傾角對X 舵的階躍響應如圖3 所示。由圖3 可見，X 舵4 片舵葉對縱傾的控制作用相當，而δ2和δ3對橫傾的控制作用明顯好于δ1和δ4，這也證實了前文的分析結果。

根據以上分析結果，可確定旋回過程的控制策略，即采用δ1或δ4或二者組合作為旋回舵；采用δ2和δ3控制縱傾和橫傾，采用δb控制深度。

3 空間旋回運動模糊控制器

采用Mamdani 方法［7］對X 舵模糊控制器進行設計，即采用語言集的形式描述控制系統的控制規則。要實現旋回過程X 舵和艏舵的自動控制，需設計以下非線性映射關系：

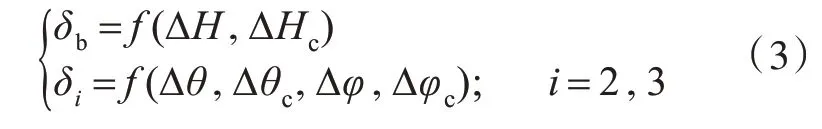
式中：ΔH為深度誤差；ΔHc為深度誤差變化率；Δθ為縱傾誤差；Δθc為縱傾誤差變化率；Δφ為橫傾誤差；Δφc為橫傾誤差變化率。

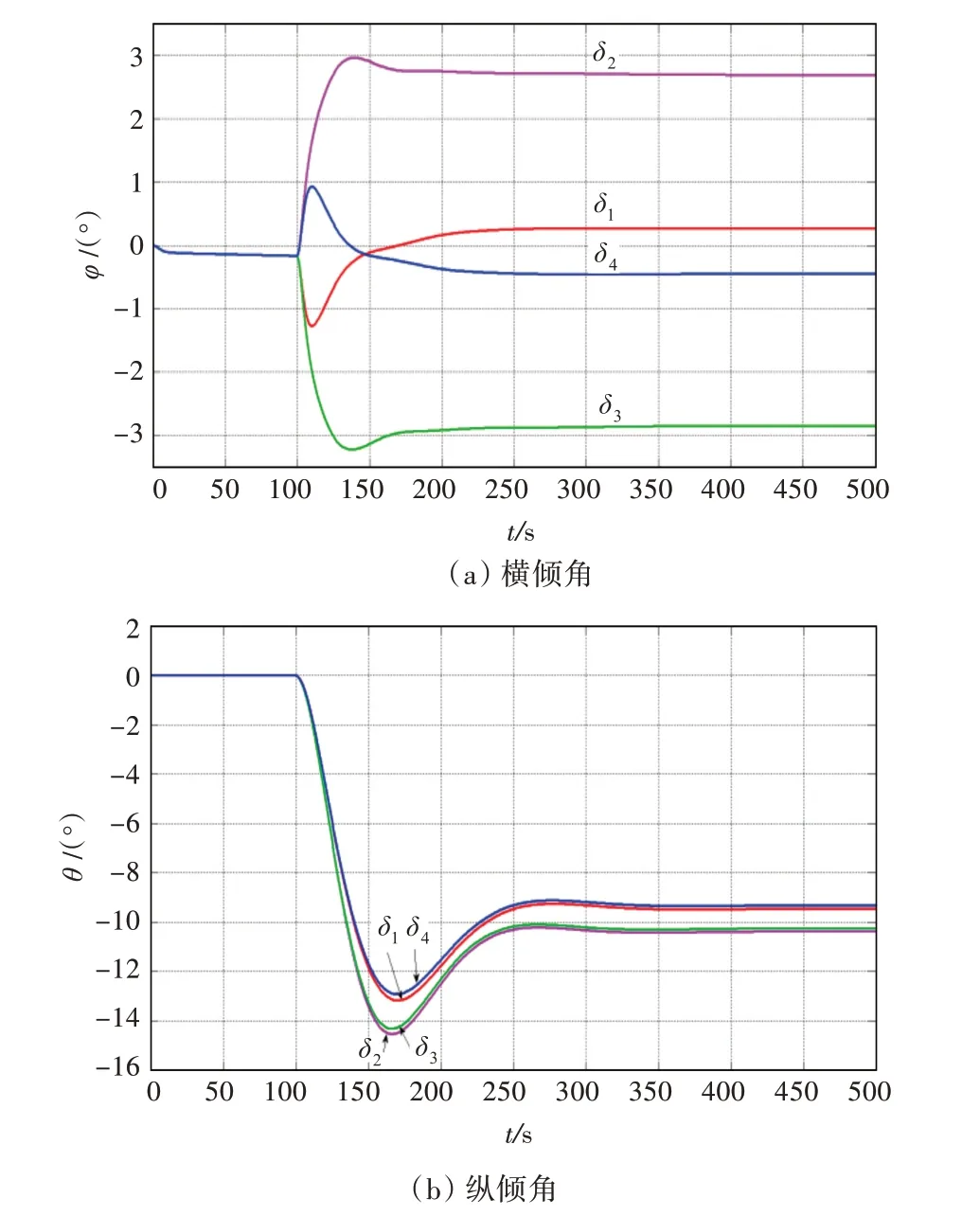
圖3 橫傾角和縱傾角對X 舵的階躍響應Fig.3 Step response of roll and pitch angle to X-rudder

3.1 論域及隸屬度函數

輸入和輸出變量論域的選擇會影響模糊控制器的動態效果，論域過大，會導致控制器響應遲緩，而論域太小，又會導致控制量出現較大的超調和波動。經反復測試，確定控制器輸入變量及其論域如表3 所示。

將6 個輸入變量（ΔH，ΔHc，Δθ，Δθc，Δφ，Δφc）和3 個輸出變量（δb，δ2，δ3）的論域劃分為13 個標準模糊集（NB（負大）、NBM（負中大）、NM（負中）…PM（正中）、PBM（正中大）、PB（正大）），對于上述若干輸入和輸出變量，模糊集的中心xi（i=1，2，…，13）取值不同，但均滿足-E=x1＜x2＜…x12＜x13=E（E 為誤差），模糊集均采用三角形隸屬度函數，由式（4）表示：

表3 模糊控制器輸入和輸出變量及論域Table 3 Fuzzy controller input and output variables and their domains

式中：μk為誤差E 相對模糊集k 的隸屬度；Ek為模糊集k 的中心對應的橫坐標。

3.2 模糊控制規則的設計

分析深度H、縱傾角θ、橫傾角φ等對艏舵和X 舵的響應規律，得到艏舵和X 舵對應于不同被控量的模糊推理規則。

3.2.1 艏舵控制規則

深度誤差ΔH以及誤差變化率ΔHc的定義為

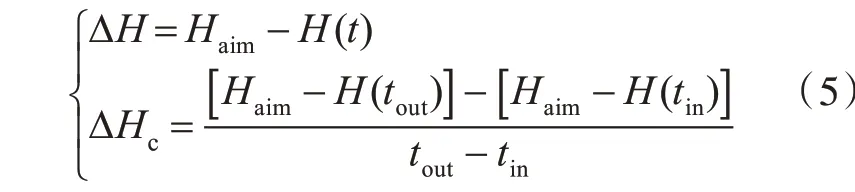
式中：Haim為目標深度；H(t)為實際深度；tin和tout為每次迭代的輸入與輸出時間，tout-tin為時間步長。根據操舵規律，對于艏舵來說，正舵角產生使潛艇上浮的作用力，負舵角產生使潛艇下潛的作用力，艏舵控制深度的規則可表示為矩陣Uδb～H：

模糊推理語言可表示為：

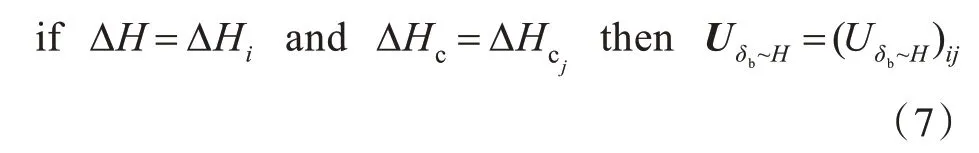
式中：i=1，2，…，13；j=1，2，…，13；ΔH1=NB，…，ΔH13=PB；ΔHc1=NB，…，ΔHc13=PB。通過艏舵模糊控制規則Uδb～H，結合ΔH 和ΔHc的隸屬度，可以得到(Uδb～H)ij及其對應的權值Kij。利用中心平均解模糊方法，得到艏舵角δb模糊控制器的輸出為

式中：Kij為ΔHi隸屬度（μ(ΔHi)）和ΔHcj隸屬度（μ(ΔHcj)）的代數積，即Kij=μ(ΔHi)·μ(ΔHcj)。

3.2.2 X 舵控制規則

X 舵的布局如圖1 所示，4 片舵葉按照圓周方向均勻分布，定義δ1～δ4的正負為：舵力沿y 方向分量為正時的舵角為正，反之為負。

1）X 舵對于縱傾的控制規則

縱傾誤差Δθ及誤差變化率Δθc的定義如式（9）所示，橫傾誤差Δφ及誤差變化率Δφc的定義與其類似。

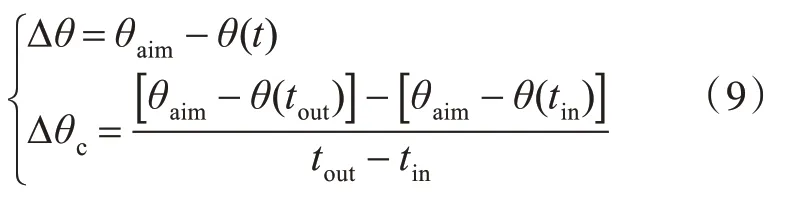
式中：θaim為目標縱傾角；θ(t)為實際縱傾角。

X 舵的4 片舵葉對于縱傾的控制規律：舵角為正時產生艏傾力矩（負縱傾），舵角為負時產生艉傾力矩（正縱傾）。通過分析，X 舵對縱傾的模糊控制規則Uδi～θ與Uδb～H相同，即Uδi～θ=Uδb～H。

2）X 舵對于橫傾的控制規則。

X 舵的4 片舵葉對橫傾的控制規律各不相同，其中：δ2正舵會產生正（右）橫傾，負舵會產生負（左）橫傾，即Uδ2～φ=-Uδi～θ，而δ3的控制規律正好與δ2對橫傾的控制規律相反，即Uδ3～φ=Uδi～θ。定義取反-Uδi～θ的算法為：將矩陣Uδi～θ中的N 和B互換。

3）X 舵控制力的分配。

為了實現自動分配X 舵對于縱傾和橫傾兩個狀態量的控制力，引入X 舵控制權值的概念，建立權值模糊控制器。控制器輸入為：（Δθ，Δφ）；控制器輸出為：（Qθ，Qφ=1-Qθ）；其中Qθ為X 舵對于縱傾的控制權限，Qφ為X 舵對于橫傾的控制權限。輸入論域為：Δθ ∈［-6，6］，Δφ ∈［-3，3］；輸出論域為：Qθ∈［0，1］，Qφ∈［0，1］。

三角形隸屬度函數如式（4）所示，將輸入和輸出論域劃分為7 個標準模糊集。控制權值模糊控制規則矩陣可表示為

從權值模糊控制器的設計過程來看，當某個被控量的誤差小而其他被控量的誤差大時，該被控量的權值也小，這符合權值的變化規律。加入權值后，X 舵模糊控制器可由式（11）表示：

4 旋回控制仿真與分析

潛艇的初始運動狀態設定為定常定深直線運動且潛艇處于完全均衡的狀態［1］，初始運動參數設定為航速10 kn，初始航行深度100 m，初始航向、縱傾角和橫傾角均為0°，所有舵角初始位置為零位。對X 舵潛艇水平面和空間旋回運動形式進行控制仿真。

4.1 定深旋回控制仿真

設 定δ1=-δ4=30°，控 制 目 標 為：θaim=φaim=0°，Haim=100 m，采用δb，δ2和δ3控制的仿真結果如圖4所示。圖中η和ξ為固定坐標系的水平面坐標。

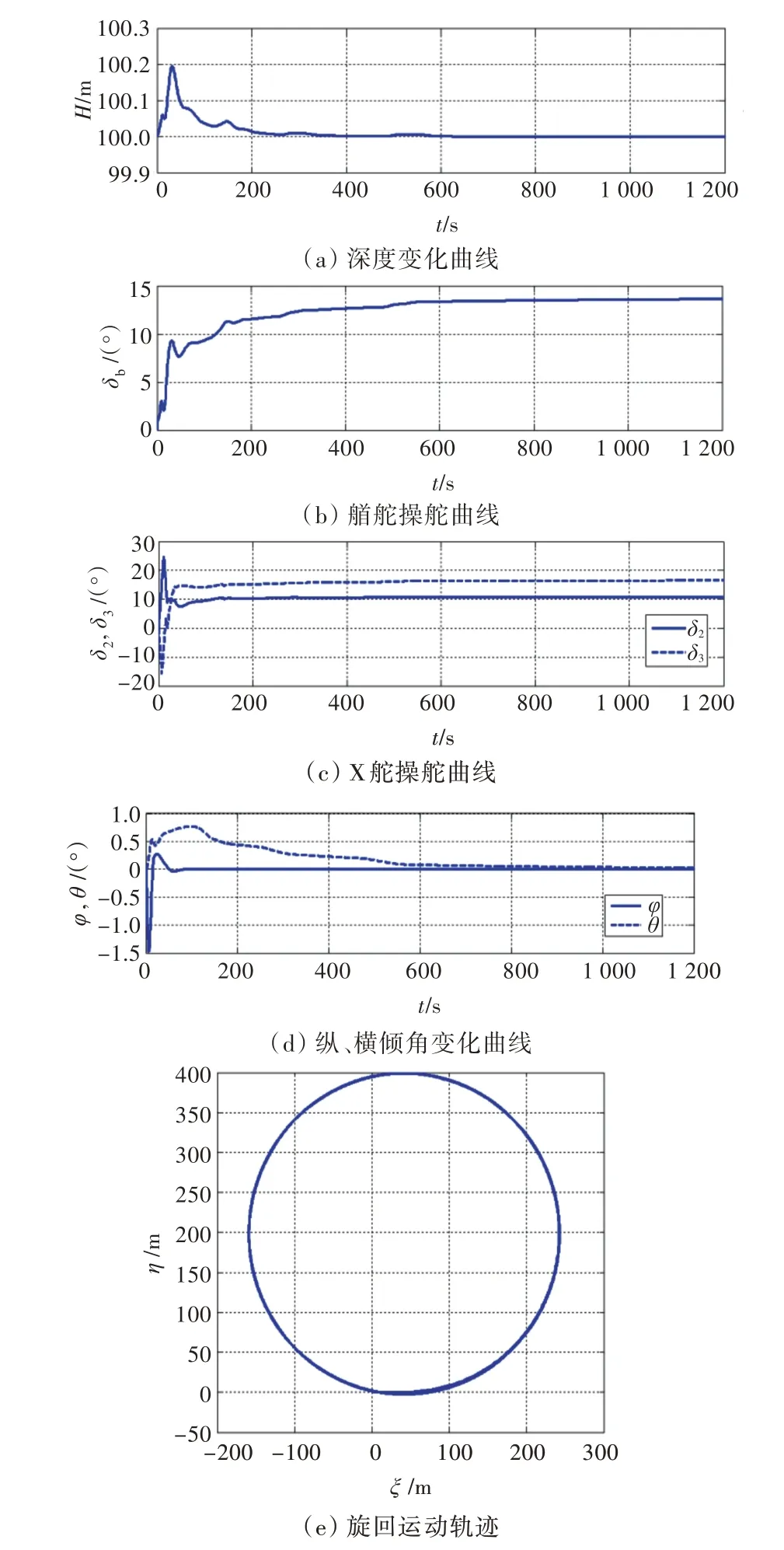
圖4 δ1=-δ4=30°，無縱傾、無橫傾定深旋回控制結果Fig.4 δ1=-δ4=30°，no pitch& no roll depth-keeping turning control results

由圖4 可見，在初始回轉階段，橫傾角的波動峰值為1.50°并迅速回0，縱傾角波動峰值為0.75°，深度波動峰值為0.2 m。進入定常回轉階段后，潛艇能保持無縱傾、無橫傾，深度保持在100 m初始深度。由仿真結果可見，采用δ1和δ4旋回時，δb，δ2和δ3控制姿態的效果較好，能夠實現無縱傾、無橫傾定深旋回。

4.2 空間變深旋回控制仿真

4.2.1 無縱、橫傾變深旋回

設 定δ1=-δ4=30°，控 制 目 標 為：θaim=φaim=0°，Haim=200 m，采用δb，δ2和δ3控制的仿真結果如圖5所示。圖中ζ為固定坐標系的垂向坐標。潛艇首先進行空間旋回運動，深度由100 m變深至200 m，然后在200 m 深度定深旋回。

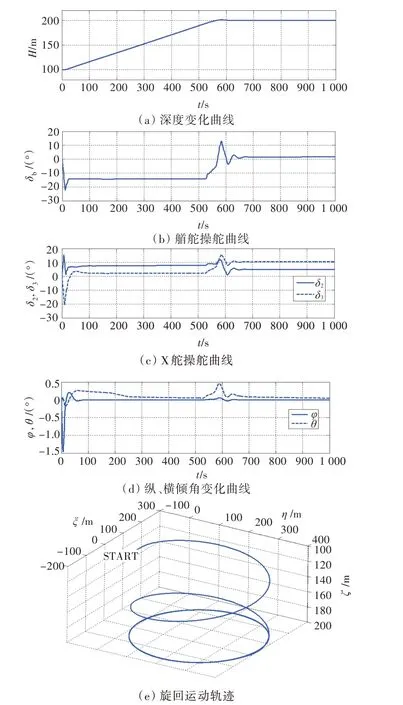
圖5 δ1=-δ4=30°，無縱傾、無橫傾變深旋回控制結果Fig.5 δ1=-δ4=30°，no pitch& no roll depth-changing turning control results

4.2.2 有縱、橫傾變深旋回

有縱、橫傾本質上相當于存在不均衡量的條件［1］，設定δ1=-δ4=10°，控制目標為：θaim=3°，φaim=2°，Haim=200 m，采用δb，δ2和δ3控制的仿真結果如圖6所示。潛艇首先進行空間旋回運動，深度由100 m變深至200 m，在變深過程中，橫傾角和縱傾角很快穩定在控制目標值θaim=3°和φaim=2°，最終，潛艇穩定在200 m 深度以設定的姿態旋回。

圖4～圖6 所示的各種旋回方式控制仿真結果表明：X 舵對于橫傾的控制能力可以優化潛艇的水下旋回運動，在X 舵角允許范圍［-30°，30°］內，可以實現任意姿態定深/變深旋回運動，這大大提高了潛艇水下運動能力。另一方面，也驗證了本文設計的X 舵旋回智能模糊控制系統的有效性。

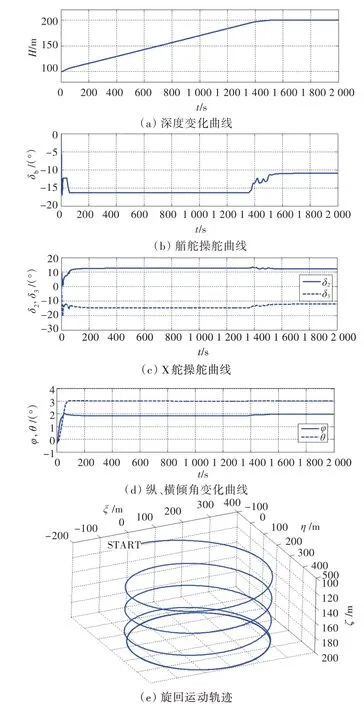
圖6 δ1=-δ4=10°，θaim=3°，φaim=2°，變深旋回控制結果Fig.6 δ1=-δ4=10°，θaim=3°，φaim=2°depth-changing turning control results

5 結 論

本文通過分析X 舵對潛艇旋回運動的控制特點，設計了X 舵潛艇空間旋回模糊控制系統，并針對潛艇水平面定深和空間變深旋回運動進行了仿真分析，結論如下：

1）建立了X 舵4 片舵葉的動態權限分配規則，為旋回過程中X 舵對于縱傾、橫傾的控制力分配提供了具體的解決方案。

2）控制系統對于潛艇定深旋回運動和空間旋回運動有著較好的控制效果，能夠較好地發揮X 舵優越的操縱性能。

3）驗證了X舵對于橫傾的控制效果，實現了無縱傾、無橫傾定深旋回運動控制，這是十字舵無法實現的，對于潛艇實際操縱有一定的借鑒參考意義。