癱船穩(wěn)性橫搖周期計算方法討論分析

馬坤，梅樹猛，于津釗

大連理工大學船舶工程學院，遼寧大連116024

0 引 言

目前，第2 代完整穩(wěn)性衡準的制定工作仍在進行當中，薄弱性評估方法已基本確定［1-2］。在癱船穩(wěn)性第1 層薄弱性衡準中，是通過簡單的計算公式來確定固有橫搖周期，但該方法沒有考慮復原力臂曲線的非線性等因素的影響［3-4］。波蘭在SDC 5/6/8 標準中提出了一種基于非線性的橫搖周期計算方法，通過該方法計算得到的橫搖周期會隨船舶橫搖角的變化而發(fā)生改變。若將該方法運用到癱船穩(wěn)性第1 層薄弱性衡準中，不僅可以解決橫搖周期計算方法的適用性問題，還可提高穩(wěn)性校核的準確性。

本文將基于以上2 種橫搖周期計算方法分別編寫程序［5］，并選取漁船、油船、消防船等不同種類的24 艘樣船共72 種載況進行計算，然后根據(jù)計算結(jié)果對比分析2 種計算方法的差異。

1 船舶橫搖周期計算方法

1.1 癱船穩(wěn)性第1 層薄弱性衡準中的橫搖周期計算方法

橫搖周期是指船舶從左舷搖向右舷再回到左舷所經(jīng)歷的時間。在癱船穩(wěn)性第1 層薄弱性衡準中，使用固定公式（1）對橫搖周期進行計算，該公式是基于70 余艘實船測試數(shù)據(jù)，由Morita 根據(jù)統(tǒng)計制定然后簡化得到［6］。

式中：系數(shù)C=0.373+0.023(B d)-0.043(Lwl100)，其中d 為吃水，Lwl為水線長；B 為船寬；GM 為經(jīng)自由液面修正后的初穩(wěn)性高。

根據(jù)式（1），可以得到船舶在單一擾動力矩下的線性橫搖幅頻曲線，如圖1 所示。從圖中可以看出，船舶線性橫搖頻率nθ為定值，不隨橫搖角θ的變化而發(fā)生任何改變。圖中，ω為波浪頻率。

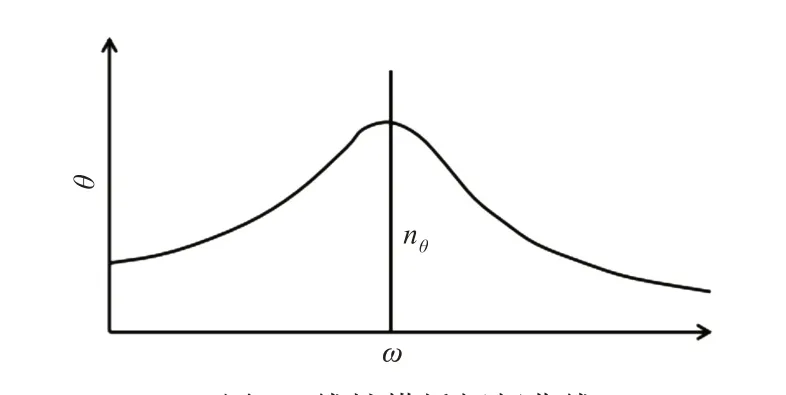
圖1 線性橫搖幅頻曲線Fig.1 Linear rolling frequency-amplitude curve

癱船穩(wěn)性第1 層薄弱性衡準考慮的條件是船舶處于不規(guī)則波和陣風環(huán)境，但式（1）計算的是船舶在靜水中且沒有任何阻力影響情況下的線性橫搖固有周期。在靜水無阻力條件下，不需要考慮阻尼力矩和擾動力矩的影響，線性橫搖，也即橫搖角相對較小，復原力矩可采用公式D·GM·θ直接進行計算。根據(jù)牛頓第二定律，可建立如式（2）所示的單自由度線性橫搖運動微分方程［7］。

式中：θ?為橫搖角加速度；ΔJθθ?為附加慣性力矩；D 為排水量。

假設全船質(zhì)量（包括附加質(zhì)量）集中于某一點，則該點距橫搖軸的距離為橫搖慣性半徑，通過該半徑，可相對容易地計算出船舶質(zhì)量慣性矩Jθ+ΔJθ。對式（2）進行簡單的推導后，便可得到現(xiàn)有橫搖周期計算公式（1）。

若嚴格按照癱船穩(wěn)性第1 層薄弱性衡準中的環(huán)境條件，受不規(guī)則橫浪等環(huán)境條件的影響，船舶橫搖勢必受到阻力作用，同時，考慮到橫搖角度較大時復原力臂曲線的非線性特征，船舶勢必會發(fā)生非線性橫搖運動。因此，通過式（1）對橫搖周期進行計算顯然不夠準確。

1.2 基于非線性的橫搖周期計算修正方法

船舶做非線性橫搖運動的主要原因是非線性的橫搖復原力矩。如圖2 所示，只有當橫搖角度θ相對較小時復原力矩M 才與θ呈線性關(guān)系，即等于D·GM·θ。特別是對于代表大多數(shù)民用船舶的曲線3，線性假設與實際差別較大，使用現(xiàn)有方法對橫搖周期進行計算會存在一定的誤差，從而導致癱船穩(wěn)性失效模式的評估結(jié)果不夠準確。

圖2 不同種類船舶復原力臂曲線示意圖Fig.2 Schematic diagram of the restoring armcurves with different types of ships

假設復原力矩取非線性關(guān)系-M=C1θ+C3θ3，則非線性橫搖運動微分方程為

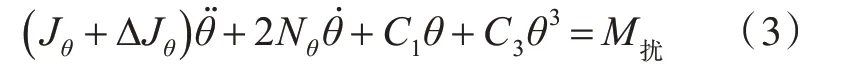
式中：Nθ為阻尼比例常數(shù)；C1，C3分別為復原力的線性和三次項系數(shù)；M擾為擾動力矩。通過數(shù)學推導，然后忽略高頻部分，便可得到船舶發(fā)生非線性橫搖運動時的橫搖頻率：

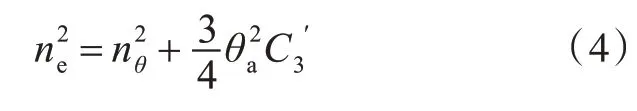
根據(jù)式（4），船舶非線性橫搖頻率ne不再是一個定值，而是橫搖幅值θa的函數(shù)。船舶在單一擾動力矩下發(fā)生非線性橫搖運動時的幅頻曲線如圖3 所示。從圖中可以看出，幅頻曲線分布在橫搖頻率曲線的兩側(cè)，且隨著橫搖頻率曲線的偏斜，幅頻曲線的峰區(qū)也會隨之呈歪斜狀。

圖3 非線性橫搖幅頻曲線Fig.3 Nonlinear rolling frequency-amplitude curves

所以，經(jīng)綜合考慮非線性復原力矩曲線的形狀以及橫搖幅值等因素的影響，對于癱船穩(wěn)性第1層衡準中的橫搖周期計算，建議采用SDC 5/6/8標準中的非線性方法［8］，即

式中：T(θa) 為特定橫搖幅值θa下的橫搖周期；GMeq(θa)為特定橫搖幅值θa下的等效初穩(wěn)性高，其計算公式為

由式（5）和式（6）可知，0～θa范圍內(nèi)的切線平均斜率以及復原力臂GZ 曲線下的面積是影響船舶橫搖周期計算結(jié)果的2 個主要因素。

2 橫搖周期修正方法的驗證與應用

波蘭對7 艘樣船共30 種載況進行了數(shù)值模擬，并基于影響橫搖周期的主要因素提出了建議的橫搖周期計算方法［8］。對比圖1 和圖3 可以發(fā)現(xiàn)，在非線性情況下，線性橫搖頻率nθ與幅頻曲線的交點一定小于橫搖幅值θa的某一點，而非線性橫搖頻率ne與幅頻曲線的交點則為橫搖幅值。

為了進一步對式（5）和式（6）進行驗證，本文對3 艘不同種類的樣船進行了計算，樣船基本信息如表1 所示。

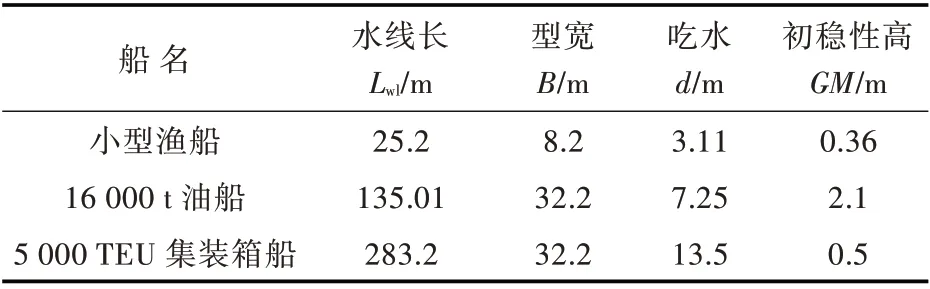
表1 樣船基本信息Table 1 Basic information of sample ships

表2 小型漁船橫搖周期簡化計算方法Table 2 Simplified method for calculating rolling period of small fishing boat

3 艘樣船的計算結(jié)果如圖4～圖6 所示。圖中：GM 為基于現(xiàn)有方法計算得到的初穩(wěn)性高；GMeq為基于修正方法，準確求得不同橫搖角對應的初穩(wěn)性高；GMeq_simple為基于修正方法，通過梯形法計算曲線面積而得到的不同橫搖角對應的初穩(wěn)性高。

由計算結(jié)果可知，GMeq與GMeq_simple基本重合，誤差主要集中在10°～15°橫搖角之間，這主要是由數(shù)值積分的梯形法則在每個區(qū)間進行線性性質(zhì)的假設所導致。不過，在該橫搖幅度范圍內(nèi)，船舶基本不會發(fā)生安全問題，所以通過近似方法計算船舶在不同橫搖角下的橫搖周期，其計算精度完全可以接受。

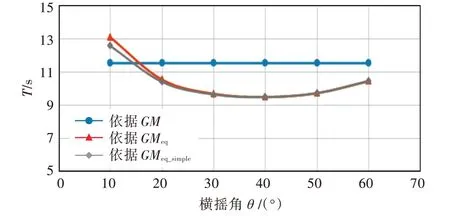
圖4 小型漁船橫搖周期計算結(jié)果對比Fig.4 Comparison of rolling period calculation results for small fishing boat

圖5 16 000 t 油船橫搖周期計算結(jié)果對比Fig.5 Comparison of rolling period calculation results for 16 000 t tanker

圖6 5 000 TEU 集裝箱船橫搖周期計算結(jié)果對比Fig.6 Comparison of rolling period calculation results for 5 000 TEU container ship

采用IMO 現(xiàn)有方法計算得到的橫搖周期與方法修正后的計算結(jié)果間確實存在一定的差異，該差異大小隨橫搖角的變化而有所不同。5 000 TEU 集裝箱船的結(jié)果差異較為明顯，當橫搖角θ=40°時，通過兩種方法計算得到的橫搖周期相差8.5 s。

使用現(xiàn)有方法計算船舶橫搖周期，一方面有可能使船舶在安全范圍內(nèi)沒有意義地避開一個速度與航線的配置組合，另一方面還有可能出現(xiàn)因共振而導致大幅橫搖的危險情況，這種情況在GZ曲線具有明顯非線性特征的船上發(fā)生的概率較大，例如，船舶最大復原力臂位于25°～30°橫搖角之間相對較小的區(qū)域范圍內(nèi)時。所以，使用修正方法代替現(xiàn)有計算方法不僅能準確得到船舶橫搖周期，還能協(xié)助船舶操縱者制定安全、經(jīng)濟、高效的航線。

3 橫搖周期計算方法對橫搖幅值計算結(jié)果的影響

3.1 橫搖幅值計算修正

使用修正的橫搖周期計算方法替代目前的常用公式，不僅可以更加準確地反映諧搖條件，還將影響第2代完整穩(wěn)性失效模式的薄弱性評估結(jié)果。

在癱船穩(wěn)性第1 層薄弱性衡準中，是通過式（7）來計算橫搖幅值［9］：

式中，k，X1，X2，r均為系數(shù)。

根據(jù)《2008 年國際完整穩(wěn)性規(guī)則》中的氣象衡準，式（7）中的波陡s 需要根據(jù)船舶橫搖周期插值確定，在6 ～30 s 的橫搖周期范圍內(nèi)，橫搖周期越大，波陡越小，且波陡范圍為0.02～0.1。由式（1），根據(jù)經(jīng)自由液面修正后的初穩(wěn)性高，即可確定船舶橫搖周期。

考慮非線性復原力臂曲線的影響后，橫搖幅值θa與橫搖周期T 之間具有特定的函數(shù)關(guān)系。同樣是對式（7）進行求解，需要通過迭代來求解橫搖幅值θa、橫搖周期T 以及波陡s的值。根據(jù)式（5）和式（6），對癱船穩(wěn)性第1 層薄弱性衡準中的評估方法進行修改。假設船舶的初始橫搖角θ0=10°，通過式（5）和式（6）計算初始橫搖角θ0對應的橫搖周期T1，得到船舶在橫搖周期為T1時對應的波陡s1和橫搖角θ1，然后按照該方法依次求得θ2，θ3，θ4……，當前、后兩次迭代所得橫搖角的差值小于10-4時，停止迭代，輸出最終計算結(jié)果。

以航行中的24 m 漁政船為例，迭代過程如表3所示。表中：Sspecific為曲線下的面積；GZspecific為橫搖角對應的復原力臂；GMspecific為等效初穩(wěn)性高。經(jīng)過8 次迭代后，得到了穩(wěn)定的收斂結(jié)果。

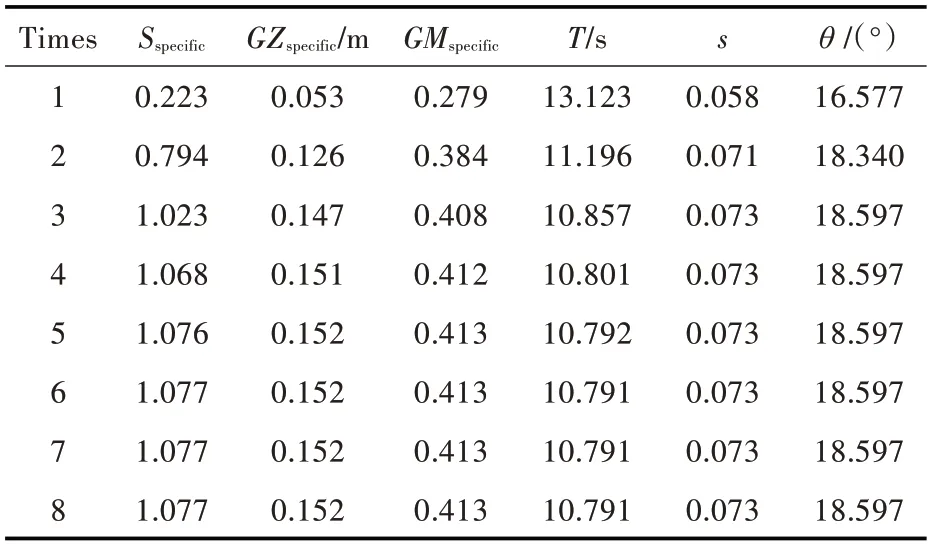
表3 24 m 漁政船橫搖幅值計算迭代過程Table 3 Iterative process for calculating roll amplitude of 24 m fishery administration ship

3.2 樣船計算結(jié)果及分析

本文選取24 艘樣船，每艘樣船包含3 種載況，對72 種載況進行計算，其中包括船長較小的24 m漁船和船長較大的186 m 油船，以確保船長較大的跨度范圍以及樣船種類的多樣性。分別通過2 種橫搖周期計算方法對橫搖幅值進行計算，計算結(jié)果按船長大小進行排序，如圖7 所示。

圖7 橫搖幅值計算結(jié)果對比Fig.7 Comparison of rolling amplitude calculation results

根據(jù)計算結(jié)果可知，通過2 種方法計算得到的橫搖幅值，其中71%的載況差值在0.5°范圍內(nèi)。不過也有空載出港的1 000 t 和2 000 t 油船、大型拖網(wǎng)漁船、6 400 方LNG 船、16 000 t 油船等部分載況計算結(jié)果的差值較大。其中，空載出港的1 000 t 油船的載況計算結(jié)果最為顯著，差值幾乎達5°。

根據(jù)式（7），橫搖幅值是通過由橫搖周期T 插值得到的波陡s進行計算的。因插值得到的波陡s變化范圍較小，使得采用2 種方法計算得到的橫搖幅值差異也不大，所以有必要輸出橫搖周期的計算結(jié)果以進行進一步的比較分析。

計算波陡s時，如果橫搖周期小于6 s，波陡s將取0.1，其不會使橫搖幅值發(fā)生改變。因此，對于橫搖周期小于6 s 的船舶，將無法進行準確的數(shù)學迭代。所以，這里僅輸出橫搖周期大于6 s 的57種載況進行比較分析，計算結(jié)果如圖8 所示。

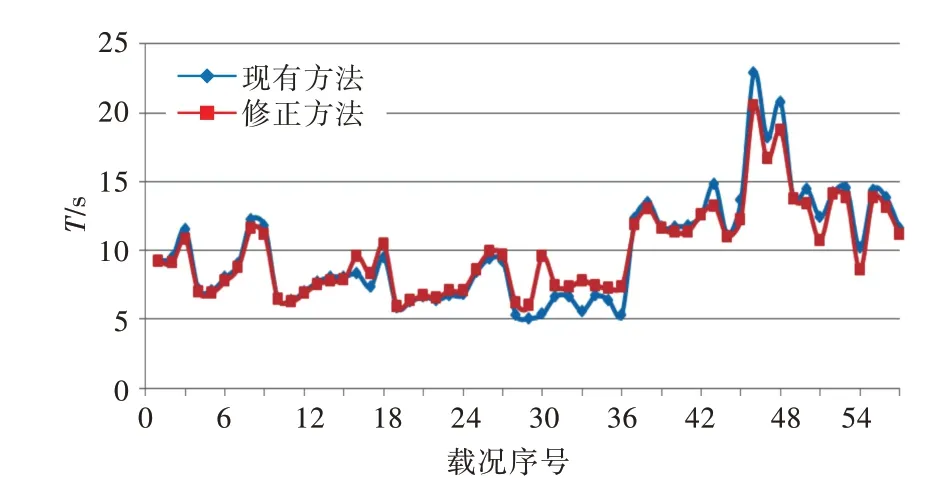
圖8 橫搖周期計算結(jié)果對比Fig.8 Comparison of rolling period calculation results

根據(jù)計算結(jié)果，通過2 種方法計算得到的橫搖周期，有22.8%的載況其差值大于1 s，差異程度和橫搖幅值相比更加明顯，且對于橫搖幅值計算結(jié)果差別較大的載況，其橫搖周期計算結(jié)果的差別同樣顯著。

輸出滿載出港LS 300 t 漁政船以及空載出港1 000 t油船的GZ 曲線進行對比分析，其中LS 300 t漁政船采用現(xiàn)有方法和修正方法所得橫搖周期計算結(jié)果相差0.17 s，幾乎一致，而1 000 t 油船的橫搖周期計算結(jié)果則相差4.2 s，差異較大。

如圖9 所示，在0°到最大復原力臂對應的橫搖角范圍內(nèi)，LS 300 t 漁政船的GZ 曲線線性特征明顯，原點處的切線斜率，也即初穩(wěn)性高為0.61 m，而本文建議使用的等效初穩(wěn)性高計算結(jié)果為0.63 m，這樣可以使橫搖周期的計算結(jié)果幾乎不變。

如圖10 所示，空載出港1 000 t 油船最大復原力臂對應的橫搖角θ≈25°，GZ 曲線非線性特點較為顯著。原點處的切線斜率，也即初穩(wěn)性高為13.363 m，而本文建議使用的等效初穩(wěn)性高計算結(jié)果僅為4.193 m，相差3 倍，橫搖周期計算結(jié)果相差較大。

圖9 LS 300 t油船滿載出港GZ 曲線Fig.9 GZ curve of LS 300 t tanker in full loaded departure

圖10 1 000 t油船空載出港GZ 曲線Fig.10 GZ curve of 1 000 t tanker in ballast departure

4 結(jié) 論

本文基于船舶運動微分方程，分析了現(xiàn)有橫搖周期計算方法的缺陷與不足，并通過3 艘典型樣船，驗證了建議方法的準確性以及便捷性。基于2 種橫搖周期計算方法編寫對應的程序，對樣船進行了計算，通過對綜合計算結(jié)果的分析，得到如下幾點結(jié)論：

1）通過原理分析以及樣船計算，發(fā)現(xiàn)現(xiàn)有橫搖周期計算方法沒有考慮GZ 曲線的非線性影響，當船舶GZ 曲線的非線性特征明顯時，使用現(xiàn)有方法計算得到的橫搖周期不夠準確，建議使用修正的橫搖周期計算方法。

2）現(xiàn)有的橫搖周期計算方法會影響癱船穩(wěn)性等失效模式薄弱性評估結(jié)果的準確性，建議使用修正的橫搖周期計算方法，通過迭代來對橫搖幅值進行計算。

3）船舶在海面上航行時，利用修正的橫搖周期計算方法可以更加準確地計算船舶處于不同橫搖角所對應的橫搖周期。