物理核心素養下幾何作圖法的運用

曲靖市第二中學 陳紅林

高中物理核心素養強調科學思維與方法，需要把復雜的物理問題通過建模使之簡單、直觀、形象化，而幾何作圖法可以充分利用“數形結合”的思想，把抽象且復雜的物理問題通過作圖轉化成簡單、直觀、形象的幾何問題。

一、幾何作圖法概述及其作用

幾何作圖法是根據題意把相對抽象復雜的物理情景通過建模畫圖直觀形象地表述出來，從而進行問題解答的一種方法。物理解題中應用幾何作圖法極為普遍，如矢量運算中的平行四邊形定則或矢量三角形、帶電粒子在磁場中運動軌跡的特點和規律、用函數圖像處理實驗數據等。在物理解題過程中巧妙地運用這些作圖方法，真正做到把物理與幾何完美地結合在一起，不僅能夠使我們在解答物理問題時發現其中的規律，也能有效地簡化解題過程，避免出現復雜的運算，提高解題效率。

二、幾何作圖法的工具及其運用

如圖1 所示，直尺、三角板、圓規、量角器和鉛筆（圖中未畫出）是幾何作圖法必備的工具，也是高考必備的考試用品。

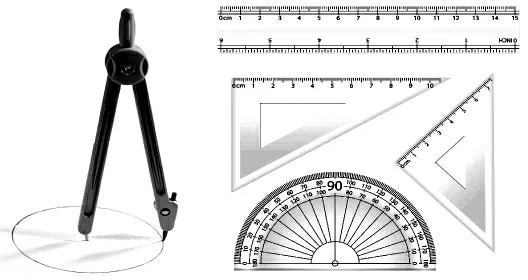
圖1

直尺、三角板既可以用來作圖，也可以用來測量長度，三角板還可以有效地運用30°、45°、60°、90°、120°這幾個特殊角度。圓規既可以用來畫帶電粒子在磁場中的運動軌跡，還可以等比例地測量長度。量角器主要用來測量任意角。

三、運用實例

例1 由于衛星的發射場不在赤道上，同步衛星發射后需要從轉移軌道經過調整再進入地球同步軌道。當衛星在轉移軌道上飛經赤道上空時，發動機點火，給衛星一附加速度，使衛星沿同步軌道運行。已知同步衛星的環繞速度約為3.1×103m/s，某次發射衛星飛經赤道上空時的速度為1.55×103m/s，此時衛星的高度與同步軌道的高度相同，轉移軌道和同步軌道的夾角為30°，如圖2所示，發動機給衛星的附加速度的方向和大小約為（ ）

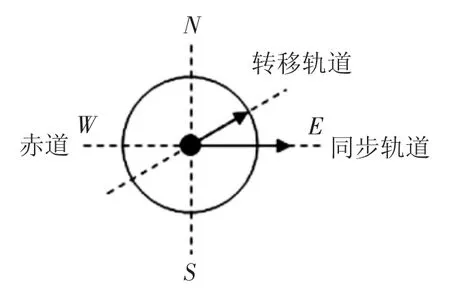
圖2

A.西偏北方向，1.9×103m/s

B.東偏南方向，1.9×103m/s

C.西偏北方向，2.7×103m/s

D.東偏南方向，2.7×103m/s

【方法一】計算法：

設衛星在轉移軌道上的速度為v2，在同步軌道上的速度為v1，附加速度為Δv。根據矢量合成作速度合成矢量三角形如圖3 所示。因為是斜三角形，根據題目所給條件只能由余弦定理得

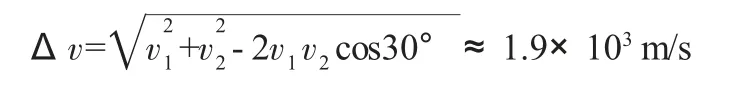
方向東偏南，故B 正確。

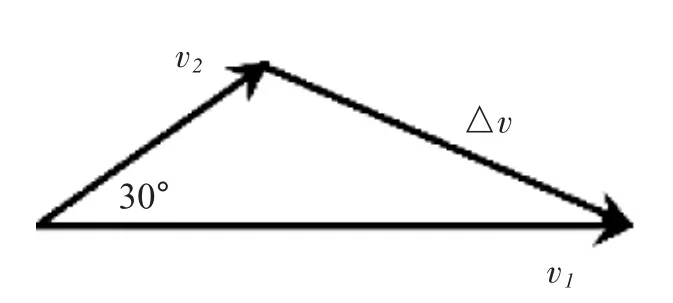
圖3

【方法二】幾何作圖法：

選1 cm 長度的線段表示103m/s 的速度，如圖4 甲所示；用30°的三角板按標度標準畫出衛星速度合成的矢量三角形如圖4 乙所示。由刻度尺可直接測量出Δv=1.9×103m/s，方向東偏南，故B 正確。

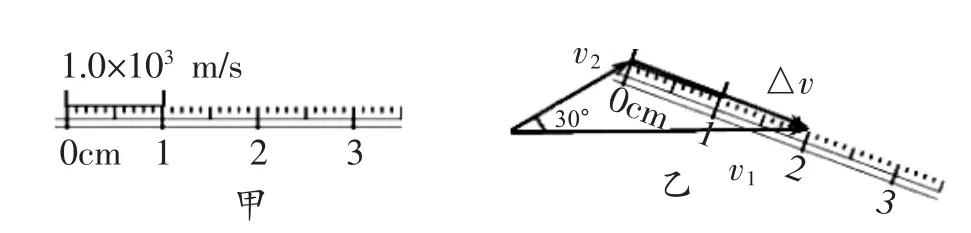
圖4

點評：此題考查的是速度的合成與分解，對比以上兩種方法，計算法由于數據和矢量三角形都不特殊，導致計算較為復雜；而幾何作圖法不需要數學計算，通過幾何作圖就可以方便快捷地直接測出結果，從而達到化繁為簡，化難為易的目的。

例2 如圖5，半徑為R的圓是一圓柱形勻強磁場區域的橫截面（紙面），磁感應強度大小為B，方向垂直于紙面向外。一電荷量為q（q＞0）、質量為m的粒子沿平行于直徑ab的方向射入磁場區域，射入點與ab的距離為。已知粒子射出磁場與射入磁場時運動方向間的夾角為60°，則粒子的速率為（不計重力）（ ）

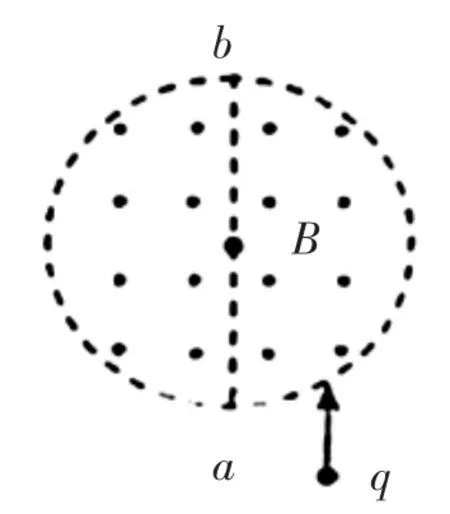
圖5

【方法一】解析法：

如圖6 所示，設入射點為A，AC 平行于ab，穿出磁場的點為B，粒子運動軌跡圓心為O，過B 點作垂線與AC 相交于C點。由題意可知，粒子射入磁場和射出磁場的夾角為60°，所以圓心角就為60 °，即∠ABO 為等邊三角形，∠BAC=30°。由直角三角形ABC 可得=R，所以帶電粒子運動的半徑為r=R。由，解得，故B 正確。

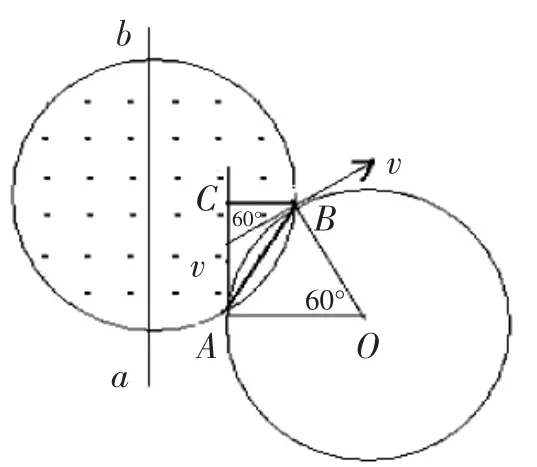
圖6

【方法二】幾何作圖法：

如圖7 所示，作入射速度的垂線即為軌跡圓心所在直線。保證偏轉角為60°和軌道半徑r 不變，用60°的三角板和圓規標準地畫出粒子的運動軌跡并確定軌跡圓心的位置O。用刻度尺就可以直接測出r=R，再由qvB=，解得，故B 正確。

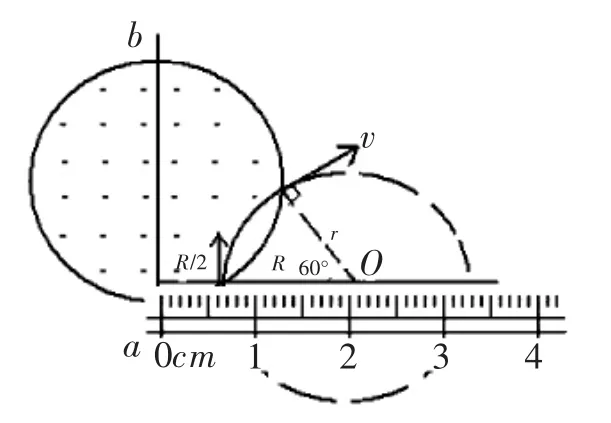
圖7

點評：此題考查的是帶電粒子在磁場中運動的問題，關鍵點在于畫出帶電粒子的運動軌跡并確定圓心位置，而找出軌道半徑r 與圓形磁場半徑R 的關系是本題的難點。我們可以用上述兩種方法求解。方法一需要幾何證明后，再計算得出r=R，要求學生數學功底扎實。方法二首先通過60°的三角板和圓規幾何作圖確定圓心位置，再用直尺快速巧妙地測量出r=R，省略了數學運算，提高了解題效率。

近年高考對學生物理核心素養的考查越來越多，這就要求學生學會正確地建立物理模型，然后應用科學的思維與方法，利用幾何作圖把復雜抽象的物理問題簡單直觀化。這不僅能大大降低解題難度，提高解題的準確率，還可以在潛移默化中培養和提升學生的物理核心素養。