寒冷地區辦公建筑負荷敏感性差異分析及應用

高 楓,朱 能

(1.天津大學 建筑學院，天津 300072; 2.天津大學 環境科學與工程學院，天津 300350)

中國疆域幅員遼闊，同一建筑熱工設計分區內由于溫度及太陽輻射強度的差異，建筑能耗水平及其重要影響參數會有所不同[1]，在建筑節能設計中不可視同一律，而寒冷地區由于需要兼顧冬季供暖和夏季制冷因此不確定性更強. 研究中，局部法[2-3]、Morris法[4-6]、Sobol法[4]等多種敏感性分析均可用于建筑能耗相關模型以篩選重要參數，但就分析結果對能耗表現的優化效果卻鮮有提及.

本文著眼于設計階段，并將辦公建筑室內環境營造負荷(包含全年供暖制冷負荷、電器及照明用電負荷)的影響因素作為研究對象，分別以北京、蘭州、喀什、拉薩4個寒冷地區為氣候背景實施Morris全局敏感性分析；之后采用相關性判定[6]對負荷進行優化，并與NSGA-Ⅱ算法的優化結果進行對比；旨在指出寒冷地區局域氣候下建筑負荷的敏感性特征差異，并在此基礎上評價基于Morris敏感性分析的優化效果.

1 方 法

敏感性分析可用于獲取參數對結果的影響性排名，但局部法并不適用于建筑能耗相關模型的非線性特征，雖可得到重要參數集合卻不推薦用于獲取敏感度排名[7-9].文中所用Morris全局敏感性分析因計算成本低、模型適應性強[9-11]，且對參數與結果的相關性有定性的描述[6,10]而常被用于分析建筑能耗模型.相比于穩健性較好的基于方差的全局敏感性分析(如：Sobol法)，在不要求因素間定量相關性描述的情況下，Morris法僅需Sobol法計算成本的幾十分之一即可得到與其基本一致的參數敏感度排名[10-11].

Morris敏感性分析中，輸出結果函數y(x)定義為

y(x)=y(x1,x2,x3,…,xk),

式中，輸入參數x的取值范圍需映射到量綱一的區間[0,1]并等分為p水平(本文p=4)，即構成k維p水平的樣本空間.之后根據OAT(one-factor-at-one-time)策略生成參數樣本，其數量常采用軌跡進行計量，每個軌跡中的k+1個樣本在運算后可得到參數的局部敏感度[12]，即元素效應EEi為

式中：i∈{1,2,3,…,k}；y(x)、yi(x)分別為xi變化前、后的輸出結果；Δ為xi變化前后對應在量綱一的區間[0,1]上的取值之差.

在對多軌跡實施運算后，可通過元素效應均值μ來表達參數的全局敏感度，但當參數相關性較強時，μ會因正負元素效應抵消而無法客觀地反映參數重要性；因此，更推薦采用μ*表達敏感度[12].μ的正、負則可用來表達參數與結果的正、負相關性，配合相關性指標σ/μ*可對參數與結果的相關形式進行描述[6]，進而對取值范圍內的參數最優值進行判定(見表1)，相關公式定義如下：

式中：r為軌跡數；σ為EEi的標準偏差；μ*為EEi的絕對均值，即敏感度.

表1 參數的相關性描述

2 模型及相關參數說明

模型為6層正方形辦公建筑，總建筑面積6 534 m2、層高3.6 m，EnergyPlus中的熱區劃分如圖1所示.

張雨生有不少雜文，關注的是貧富差距。《貧富差距的代際傳承》是他在這方面的代表作。中國富豪財富積累的時間超短，“富二代”就是“憑資本分配養育的一代”。張雨生說：“我想點明的是，在貧富差距的代際傳承中，政府需要擔當起調節這個差距的責任。”并且具體提出“政府應該不應該啟動遺產稅”的問題。與此文著重說“富”的一端不同，《向農民工深鞠一躬》說的是“貧”的一端，他說得擲地有聲：“若有人編著這個時期的史冊，沒有農民工的輝煌篇章，我敢說，那便缺失了創造歷史的主體。”他在新春前夕用“深鞠一躬”的方式，表達了對農民工的敬意。

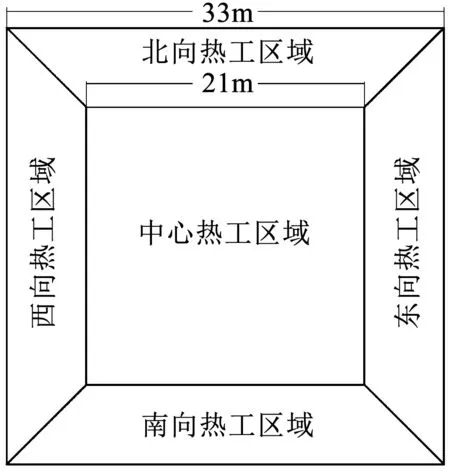
圖1 辦公建筑熱區劃分

2.1 輸入參數

模型輸入參數以圍護結構熱工參數為主，輔以室內負荷參數、室內供暖制冷設定溫度等(共計42個).由于針對設計初期，并未對暖通空調參數做過多探討；此外，為減少參數數量采用等效法將圍護結構簡化為單一結構層.

表2中，通過結構厚度、導熱系數、比熱容、密度對非透明圍護結構的熱工性能進行描述，并將屋頂及外墻的傳熱系數通過導熱系數和厚度控制在GB 50189―2015《公共建筑節能設計標準》規定[13]中寒冷地區的限值以內，樓板、地面、內墻則參考常規構造.室內供暖制冷設定溫度、外窗及室內負荷參數取值見表3，其中外表面空氣滲透率約相當于2～7級門窗氣密性[14].表皮輻射參數設定見表4，其中太陽輻射吸收系數代表結構表皮對太陽輻射的吸收能力(波長在0.300～2.537 μm的輻射)，而吸熱系數則針對構件間的輻射換熱(波長大于2.500 μm的輻射).

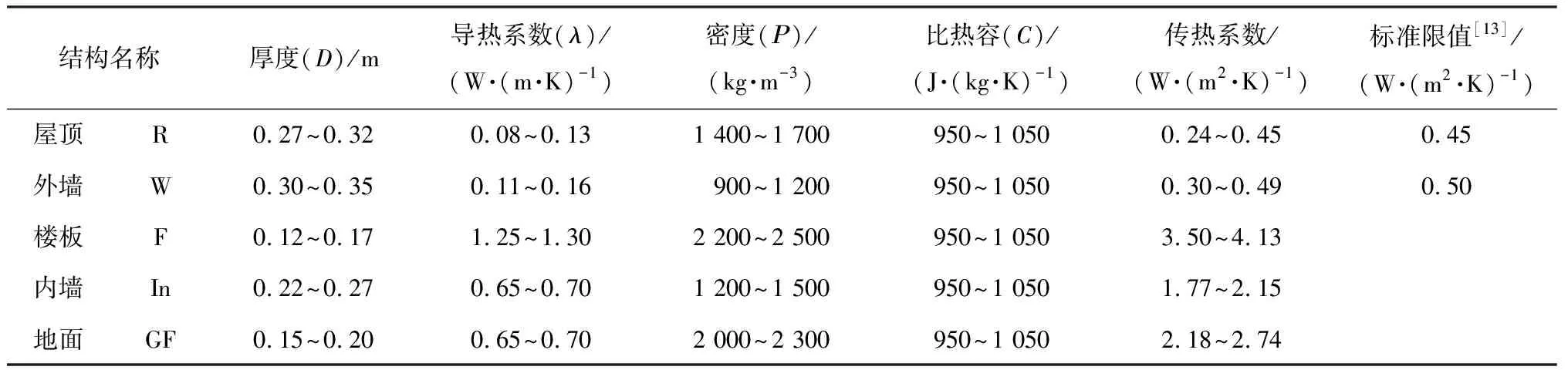
表2 非透明圍護結構參數取值

注：括號內為物理量簡稱，R(D)即為屋頂厚度；采用等效法后以上取值均代表結構均值.

表3 外窗、室內負荷、供暖制冷設定溫度參數取值

Tab.3 Parameter setting of window, internal loads, and set-point temperatures

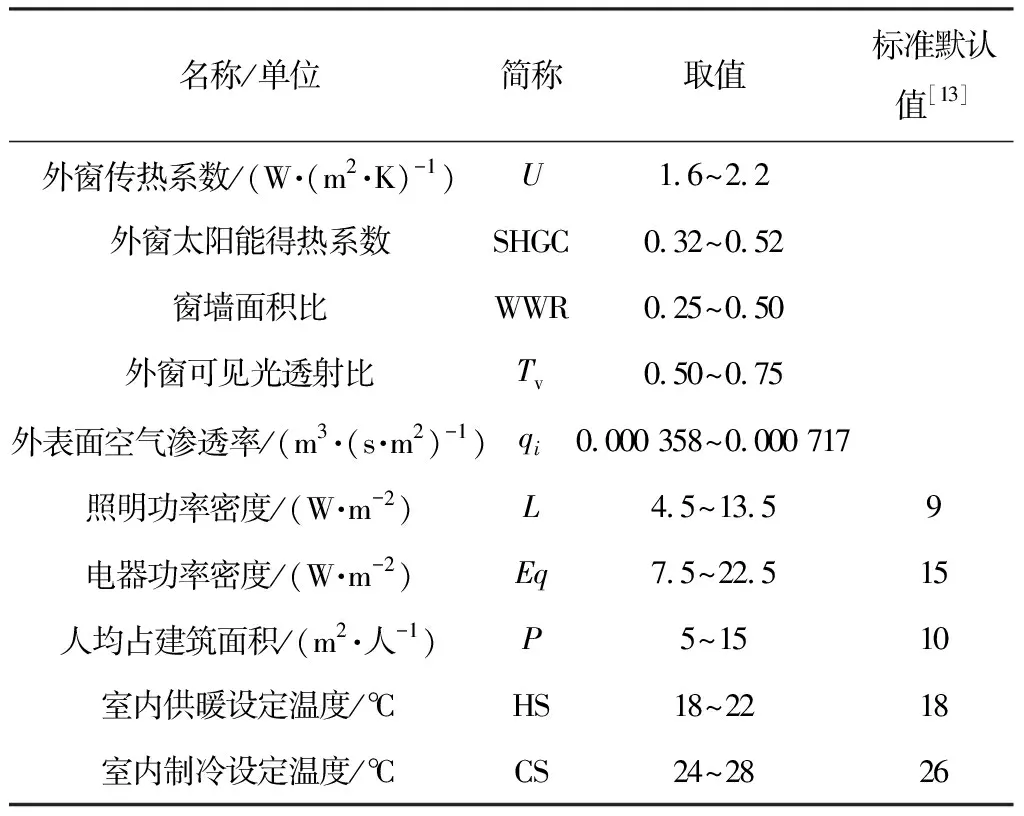
名稱/單位簡稱取值標準默認值[13]外窗傳熱系數/(W·(m2·K)-1)U1.6～2.2外窗太陽能得熱系數SHGC0.32～0.52窗墻面積比WWR0.25～0.50外窗可見光透射比Tv0.50～0.75外表面空氣滲透率/(m3·(s·m2)-1)qi0.000 358～0.000 717照明功率密度/(W·m-2)L4.5～13.59電器功率密度/(W·m-2)Eq7.5～22.515人均占建筑面積/(m2·人-1)P5～1510室內供暖設定溫度/℃HS18～2218室內制冷設定溫度/℃CS24～2826

表4 結構表皮輻射相關參數設定

Tab.4 Setting of radiation-related parameters of structure surface

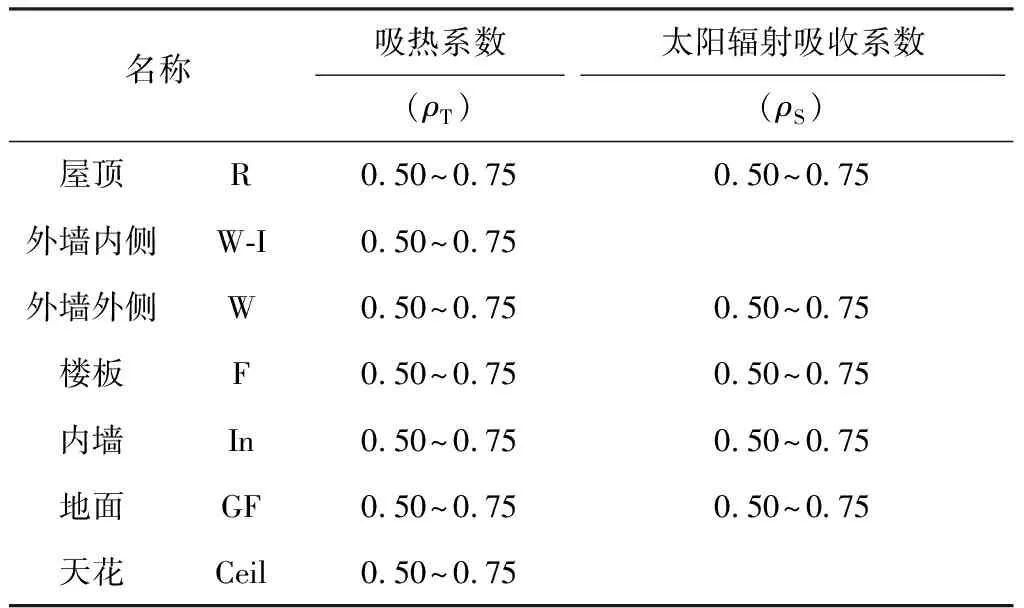
名稱吸熱系數太陽輻射吸收系數(ρT)(ρS)屋頂R0.50～0.750.50～0.75外墻內側W-I0.50～0.75外墻外側W0.50～0.750.50～0.75樓板F0.50～0.750.50～0.75內墻In0.50～0.750.50～0.75地面GF0.50～0.750.50～0.75天花Ceil0.50～0.75

注：括號內為物理量簡稱，R(ρT)即為屋頂表面吸熱系數.

圖2為北京、蘭州地區辦公建筑運行設定，其中系統高負荷運行時段設為8:00-18:00，但喀什及拉薩由于與北京所屬時區差異較大，因此需分別延后1.5 h和1.0 h.此外，人體活動水平及人均新風量分別設為100 W·人-1和30 m3·(h·人)-1.

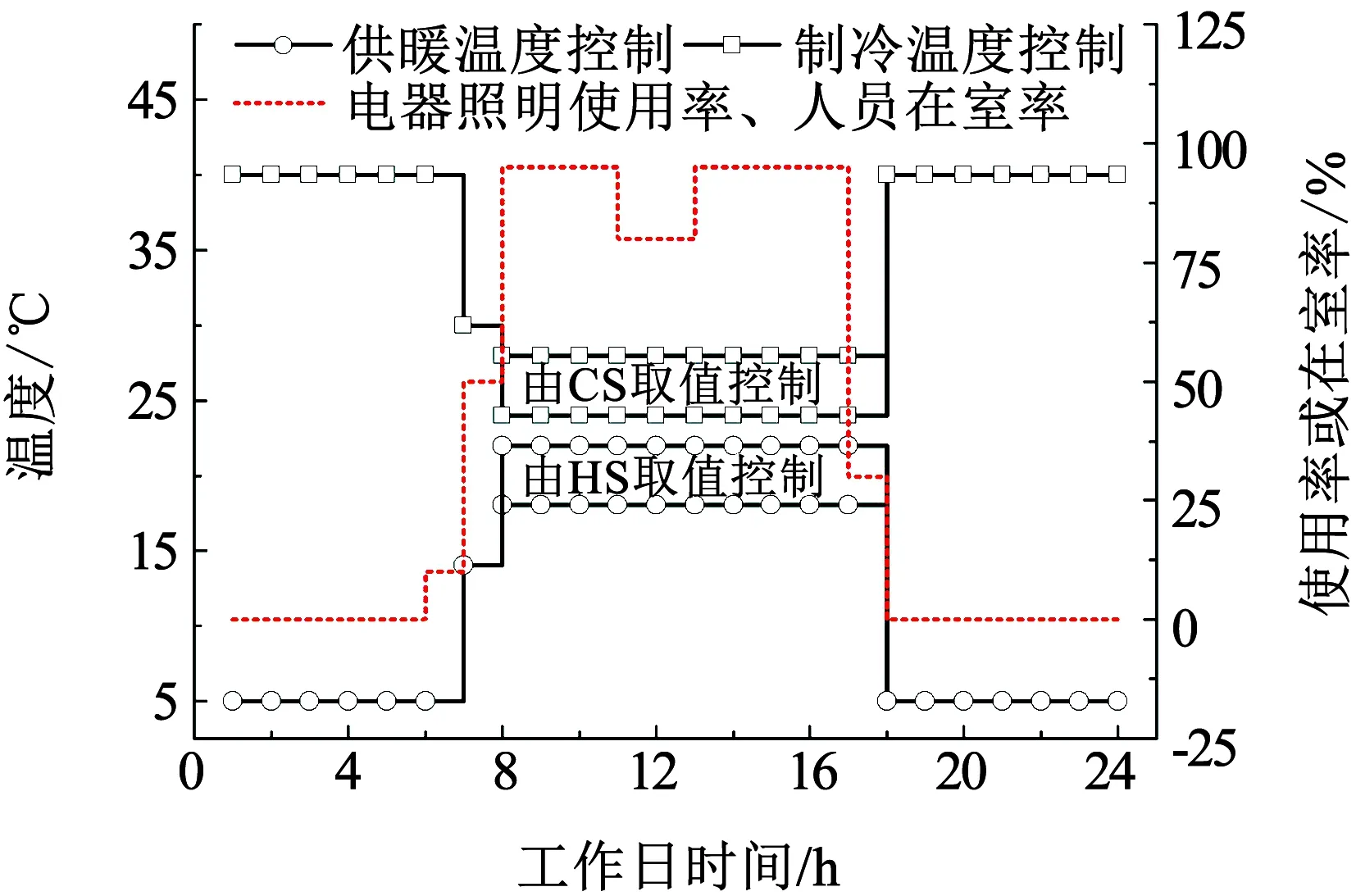
圖2 標準建筑運行設定

2.2 輸出結果

Morris敏感性分析中負荷模型的輸出結果包含建筑供暖負荷、制冷負荷、電器及照明用電負荷；為表征建筑能耗水平將其合并為建筑室內環境營造負荷，并以單位面積全年累計量的形式進行分析.

2.3 氣候參數

中國寒冷地區地域廣闊，室外溫度、太陽輻射強度、以及局部氣候上會存在一定差異，因此篩選地理跨度(經度、緯度、海拔)較大的4所城市作為氣候背景，分別為北京、蘭州、喀什、拉薩，其地理及氣候信息見表5.

表5 各地區地理及氣候信息(數據源自文獻[15])

3 結果分析

圖3為本文分析流程圖，包含EnergyPlus中的基礎設定及各步驟所需軟件，其中批量模擬通過EnergyPlus和Jeplus實現.

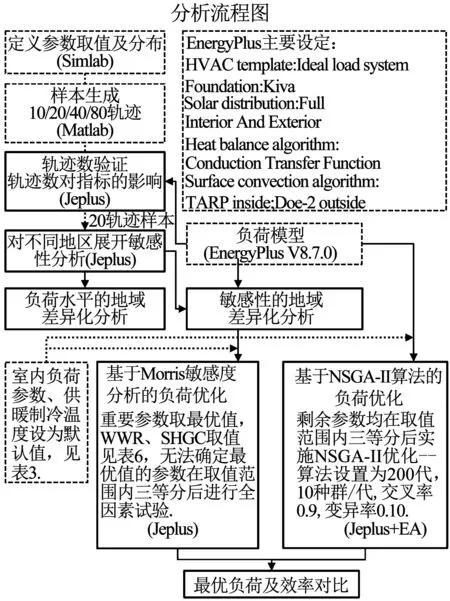
圖3 分析流程圖

3.1 軌跡數驗證

Morris敏感性分析中，結果的準確性取決于樣本對樣本空間的全局性表達，而這與樣本數量及采樣方法關聯較大.文中所用SU(sampling uniformity)采樣法從300組樣本中篩選出歐幾里得距離最大的一組，并視其具有最佳全局性[16].而另一方面，由于模型、參數數量及取值的不同，軌跡數的確定還需單獨驗證.

圖4 軌跡數對敏感度和相關性的影響

Fig.4 Impact of trajectory number on sensitivity and correlation indices

3.2 負荷分析

全局樣本下，各地區建筑負荷分布如圖5所示.就室內環境營造負荷的整體水平而言，北京>喀什>蘭州>拉薩，其間的差距主要源自各地區的供暖和制冷負荷.與制冷負荷不同，采暖度日數并不能很好地反映當地的供暖負荷水平，尤其是在采暖度日數最高的拉薩地區(3 425 ℃·d)反而供暖負荷水平最低，單位面積全年累計供暖負荷均值僅為31.6 kWh·(m2·a)-1.

該現象與工作時段當地溫度及太陽輻射強度有關.圖6中可見拉薩地區在工作時段±2 h內(此處考慮延遲作用)的室外溫度月均值在冬季最低約為0 ℃，明顯高于其他3個地區；不僅如此，當地該時段的冬季太陽輻射強度月均值大于450 W/m2，同樣高于其他地區.在此綜合作用下，拉薩表現出最低的供暖負荷水平.

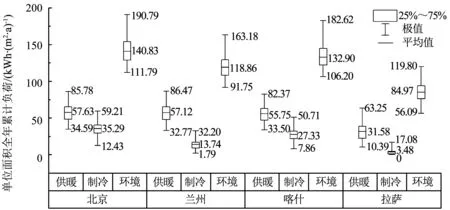
圖5 敏感性分析中各地區建筑負荷分布

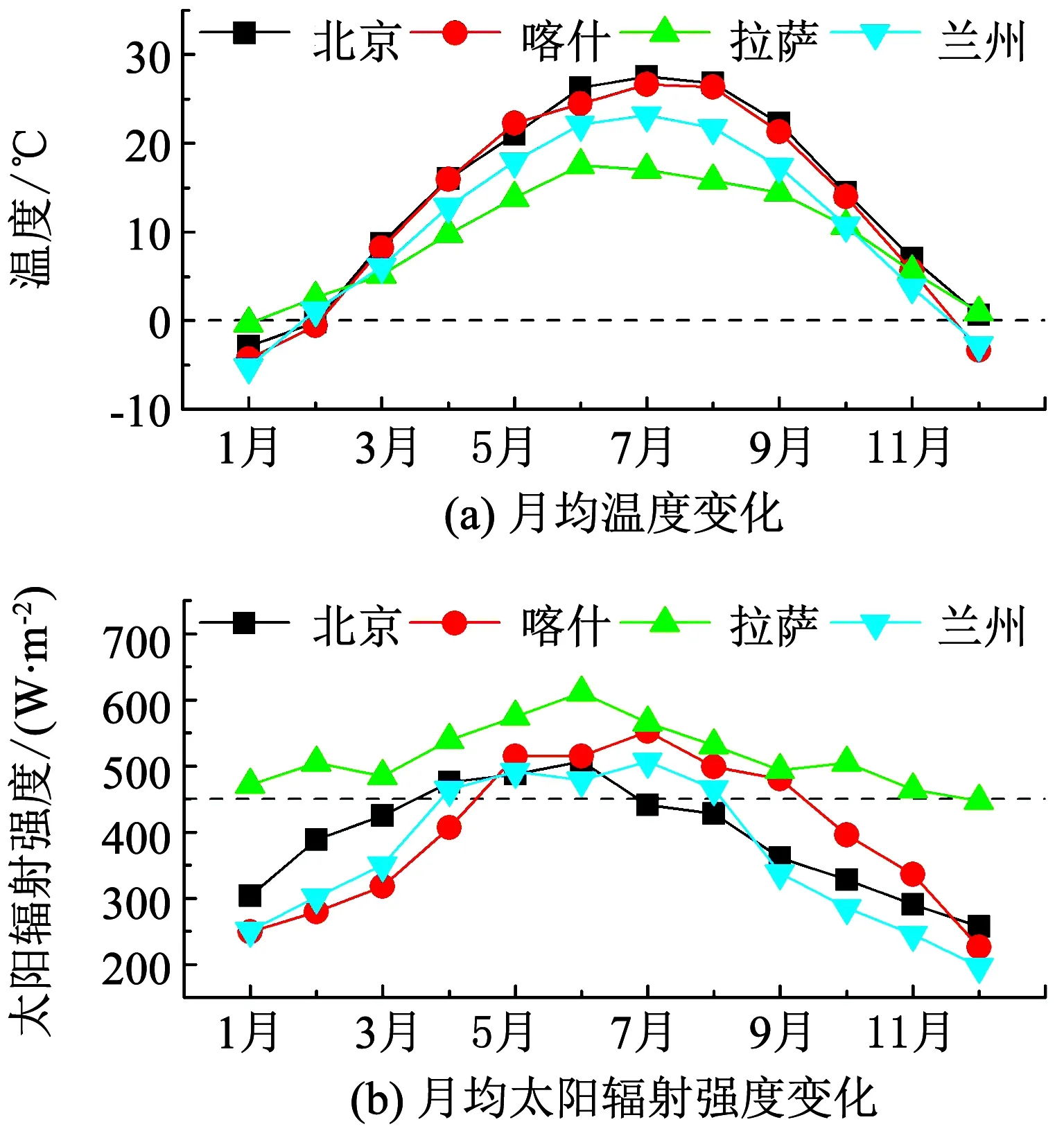
圖6 溫度、太陽輻射強度月均值(數據源自文獻[17])

Fig.6 Monthly mean value of temperature and solar radiation intensity(data from literature[17])

3.3 敏感性分析

為排除低敏感參數的干擾，將各地區敏感度排名前1/3的參數定義為高敏感參數并做進一步分析(如圖7所示).4個地區中，室內負荷參數及供暖制冷設定溫度排名靠前，且除人均占建筑面積(P)外均可視為與室內環境營造負荷呈線性相關.排名靠后的圍護結構參數中，導熱相關參數，如：U、R(λ)、W(D)，與室內環境營造負荷在各地區均為單調相關且正負相關性一致，因此具有相同的最優值.

敏感性的地域差異則主要表現在兩方面，首先是拉薩地區輻射相關參數影響的突顯，圖7(d)中可見屋頂及外墻的外表面太陽輻射吸收系數與其結構平均導熱系數的敏感度相近.另外，WWR和SHGC與負荷的正、負相關性存在地域差異，如WWR在北京、蘭州、喀什均與室內環境營造負荷呈正相關而在拉薩卻為負相關，對此需考慮朝向并做進一步分析.

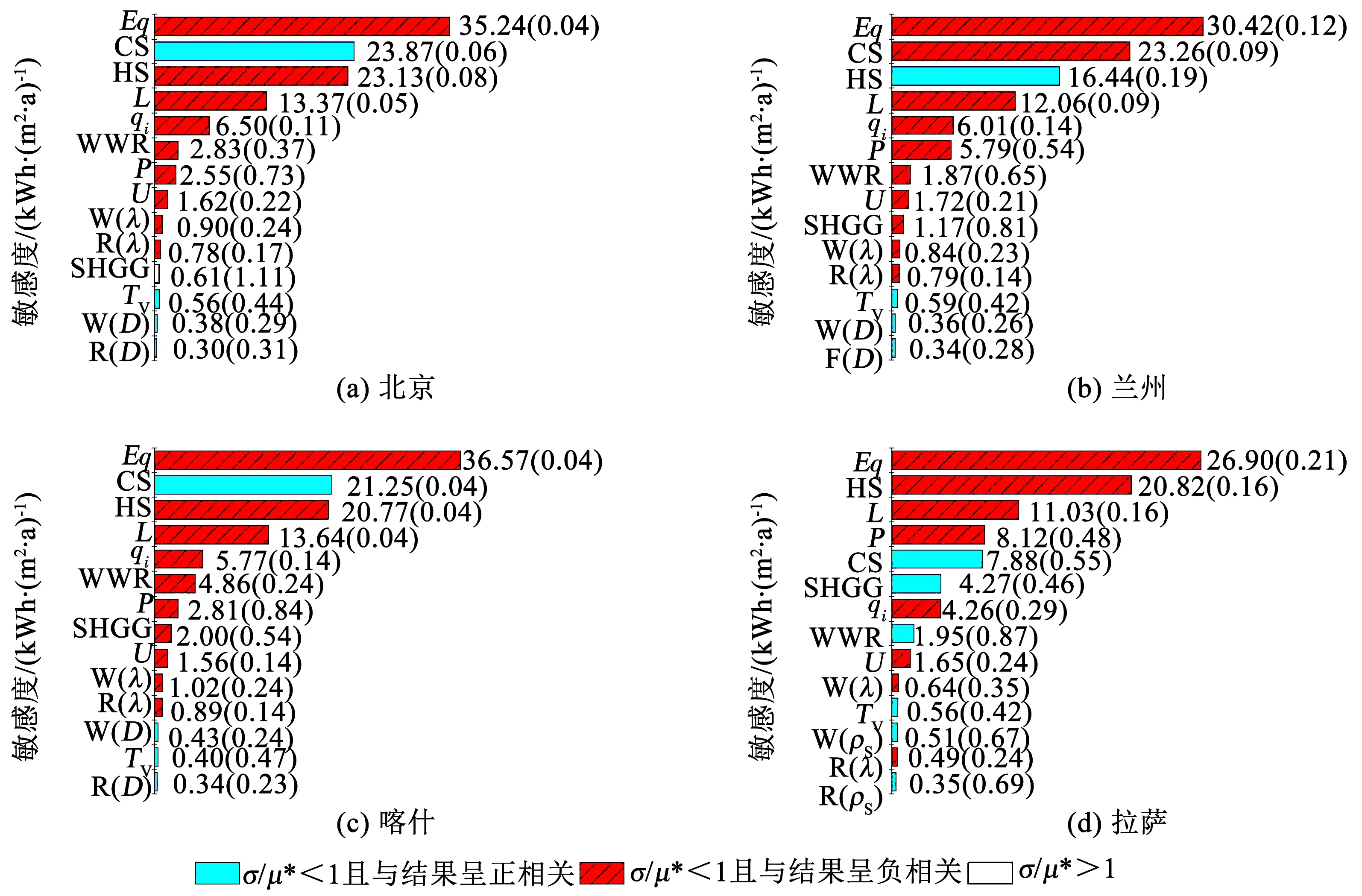
圖7 高敏感參數敏感度及相關性(括號內為相關性)

表6、7為各朝向外圍熱區中SHGC和WWR對室內環境營造負荷的敏感度以及根據相關性確定的取值范圍內最優值；可見，相比于圖7中的建筑整體敏感度，二者對外圍空間負荷的影響有顯著提升，其中SHGC多在南向影響最強(喀什為西向)；而WWR多為西向最強(拉薩為南向).對于最優值，二者多數情況下都存在朝向差異或不確定性，僅在拉薩(SHGC: 0.52)和喀什(WWR: 0.25)分別表現出相同的各朝向最優值.

表6 SHGC在不同朝向的敏感度及最優值

Tab.6 Sensitivity and optimal value of SHGC in different orientations in each region

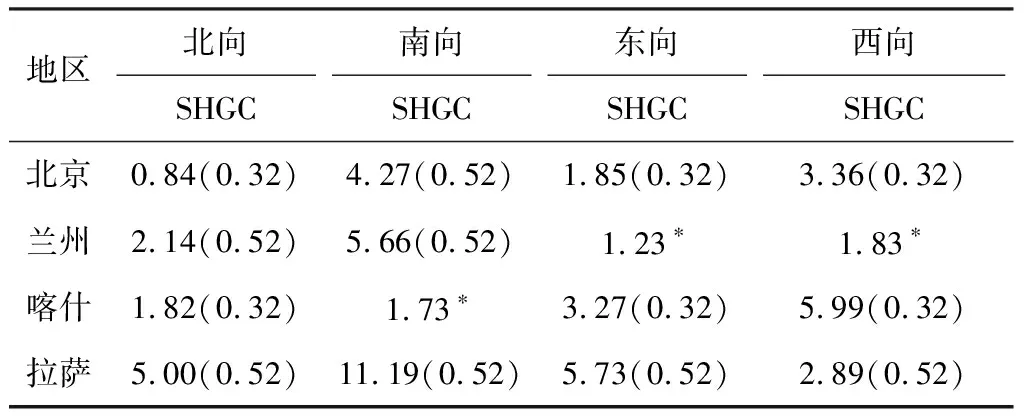
地區北向南向東向西向SHGCSHGCSHGCSHGC北京0.84(0.32)4.27(0.52)1.85(0.32)3.36(0.32)蘭州2.14(0.52)5.66(0.52)1.23?1.83?喀什1.82(0.32)1.73?3.27(0.32)5.99(0.32)拉薩5.00(0.52)11.19(0.52)5.73(0.52)2.89(0.52)

注：括號內為最優值；*代表參數的相關性大于1，最優值需進一步確定.

表7 WWR在不同朝向的敏感度及最優值

Tab.7 Sensitivity and optimal value of WWR in different orientations in each region

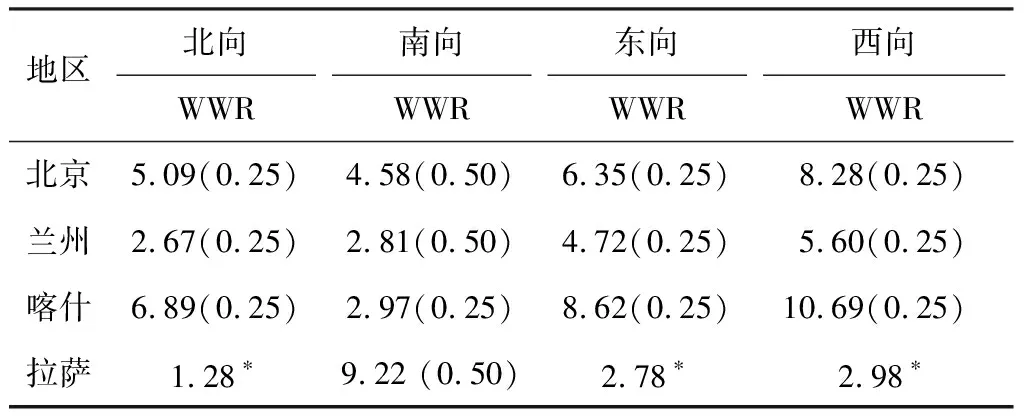
地區北向南向東向西向WWRWWRWWRWWR北京5.09(0.25)4.58(0.50)6.35(0.25)8.28(0.25)蘭州2.67(0.25)2.81(0.50)4.72(0.25)5.60(0.25)喀什6.89(0.25)2.97(0.25)8.62(0.25)10.69(0.25)拉薩1.28?9.22 (0.50)2.78?2.98?

注：括號內為最優值；*代表參數的相關性大于1，最優值需進一步確定.

3.4 室內環境營造負荷優化

在對各朝向外圍空間實施Morris敏感性分析后，無法確定最優值的參數已僅剩個別外窗參數，數量較少——北京0個、蘭州2個、喀什1個、拉薩3個(見表6).此時可對該類參數采用全因素試驗來獲取最優室內環境營造負荷.為評價該方法的優化表現，將NSGA-Ⅱ算法的優化結果及耗時與之進行對比，操作流程及設定如圖3所示.由于室內負荷參數取值已經固定，圖8中著重突顯NSGA-Ⅱ算法對供暖及制冷負荷的優化效果，可見200代(10種群/代)時的帕累托前沿重疊度已較高，繼續優化的意義不大.表8中可見與耗時逾6 h的NSGA-Ⅱ優化結果相比，基于Morris敏感性分析的最優解更小，且總耗時可至少降低1/3(約2 h).此外，由全因素試驗所得不確定參數的最優值如下：蘭州(SHGC東∶0.52，SHGC西∶0.52)，喀什(SHGC南∶0.52)，拉薩(WWR北∶0.33，WWR東∶0.33，WWR西∶0.25).

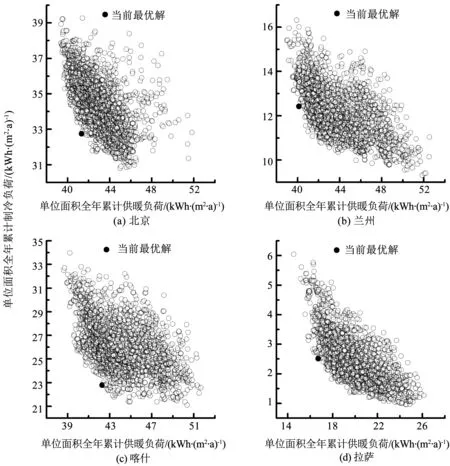
圖8 NSGA-Ⅱ算法優化所得各地供暖制冷負荷分布

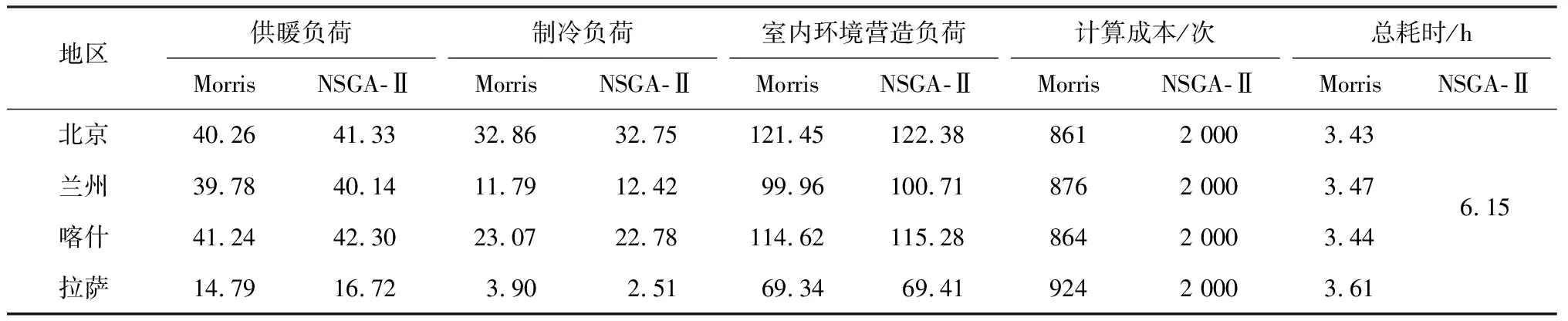
表8 最優室內環境營造負荷及總耗時對比

注：總耗時為模擬耗時+額外耗時，Morris和NSGA-Ⅱ的額外耗時分別約為1.0 h和0.5 h；文中模擬采用I7-8700K處理器+16 g內存，可12線程并行運算，單次模擬平均耗時122 s.

4 結 論

1)相比于敏感度(μ*)，相關性(σ/μ*)受樣本數量影響更為顯著；若單純考慮敏感度，樣本數量可酌情降低，文中基于SU采樣法的樣本數量可至少從20降至10軌跡.

2)采暖度日數并不能很好地反映寒冷地區辦公建筑的供暖負荷水平，更應綜合考慮工作時段室外溫度及太陽輻射強度.

3)圍護結構參數中，輻射相關參數在太陽能資源豐富地區應予以重視.以拉薩為例，外墻及屋頂外表面太陽輻射吸收系數對室內環境營造負荷的影響可接近相應結構的平均導熱系數.

4)在節能標準[13]對寒冷地區建筑圍護結構的熱工性能限定下，各地屋頂、外墻的導熱系數和厚度以及外窗傳熱系數與室內環境營造負荷均表現為單調相關且正負相關性穩定.而另一方面，相比于敏感度的朝向差異，SHGC和WWR的相關性在地域及朝向上的差異會直接影響對參數最優值的判斷，在節能設計中應予以重視.

5)200代(10種群/代)的NSGA-Ⅱ優化結果可證實基于Morris敏感性分析的優化在節能設計中的有效性，且顯示出其效率上的優勢.