帶有雙曲正切加權函數的落角約束最優制導律

陳 琦，楊 靖,王中原，常思江

(1.南京理工大學 能源與動力工程學院,南京 210094; 2.中國兵器工業集團203所,西安 710065)

在現代戰爭中，為了提高導彈的毀傷效果，往往希望導彈在命中目標時能夠保持特定的攻擊角度，例如：為了攻擊坦克或軍艦的薄弱部位，通常要求導彈以一定的落角命中目標；對于逆軌攔截高速運動目標，則要求彈道導彈能夠對來襲彈頭進行迎頭攔截.因此，研究帶有落角約束的末制導律具有重要的意義.

針對含有落角約束的攔截打擊問題，相關學者在傳統比例導引律的基礎上提出了許多新的研究方法.文獻[1]通過在傳統比例導引律的視線角速度項上增加一個偏置量，以實現落角約束的要求.文獻[2]則進一步利用能量最小準則優化了偏置參數，提高了制導律的控制效率，使得優化后的偏置比例導引律更適合于大氣層外攔截.文獻[3]針對靜止目標，通過調整制導系數使得比例導引律滿足期望的攻擊角度，同時為了進一步提高大范圍落角約束的適應性，引入了兩階段制導系數切換策略，取得了不錯的制導效果.文獻[4]則進一步將文獻[3]中的方法擴展到了目標運動的情形.隨著控制理論的發展，越來越多的學者基于現代控制理論提出了新型的末制導律.文獻[5]改進并拓展了圓軌跡導引算法，提出了一種適應再入飛行器速度大小變化的帶有落角約束的新型制導律.文獻[6]利用模型預測靜態規劃技術，設計了彈道導彈再入末制導律，該制導律可以在滿足落角約束的基礎上對靜止和機動目標進行打擊，同時避免了運動模型的線性化，具有較高的制導精度. 基于滑模控制理論和動態面控制方法，文獻[7]圍繞機動目標的打擊問題，設計了一種考慮自動駕駛儀動態特性的帶角度約束制導律.文獻[8]采用擴張干擾觀測器來估計導彈的速度及目標的機動信息，設計了帶角度約束的有限時間收斂末制導律.

最優控制可以保證特定性能的最優性，同時還可以較為方便地處理各種約束條件，在制導律的設計中有著較大的優勢，因此越來越多的學者將最優控制理論應用于帶有落角約束的末制導律的設計中.文獻[9]首先將末制導問題轉化為線性二次型問題，然后應用次優理論設計了再入式飛行器帶有落角約束的末制導律. 通過求解能量最優控制問題，文獻[10]同時研究了控制系統為一階慣性環節和無慣性環節的落角約束最優制導律，為了提高制導精度，文獻[10]還給出了3種剩余飛行時間的估算方法. 基于最優控制理論，同時考慮目標機動的情形，文獻[11]為反坦克導彈和反艦導彈設計了落角約束最優制導律.文獻[12]考慮了導彈具有軸向加速度的情形，應用Schwarz不等式方法，設計了一種帶有重力輔助的最優落角約束末制導律.

在基于最優控制的制導律設計中，控制能量被廣泛用作性能函數，其中控制能量的加權函數對制導效果有著直接的影響，不同的加權函數會使導彈產生不同的飛行軌跡和制導指令分布.文獻[13]以指數函數作為加權函數，設計了防空導彈的最優制導律.考慮了空氣密度的變化，通過合理地設計指數函數，使得導彈在飛行高度增加的過程中，逐漸提高控制能量的權重，以此來限制制導指令，使導彈在接近目標的過程中，需用過載逐步趨向于零.文獻[14-15]將剩余飛行時間n次方的倒數作為加權函數，設計了帶有落角約束的最優末制導律，該制導律可使導彈過載在制導末端趨于小值，提高了導彈在制導末端的抗干擾能力.文獻[16]則對制導初始指令的分布進行了著重考慮，設計了一種Gaussian加權函數，該加權函數可以使導彈過載在導引起始階段保持較小的值，進而降低了導彈對初始狀態誤差的敏感度.文獻[17]設計了一種基于正弦函數加權的落角約束最優制導律，通過調節正弦函數的周期和相位，該制導律可以實現導彈在制導始端和末端均產生較小的過載.文獻[18]應用Schwarz不等式方法，研究了帶有任意加權函數的最優制導律的一般表達式，但是為了能夠得到解析解，該方法要求加權函數的逆的一次到三次積分都能求出解析表達式. 上述研究主要是采用極小值原理和Schwarz不等式等方法來求解最優控制問題，這種方法精度較高，但對于復雜的問題，該方法推導過程較為繁瑣.文獻[19]利用黎卡提方程來求解最優制導律，但在一般情況下，求解黎卡提方程的解析解難度較大，為此，文獻[20]使用黎卡提方程的穩態解來求解最優制導律，這種方法降低了求解難度，但只是一種近似的處理方法，有一定的局限性.針對上述問題，文獻[21]采用滾動時域的方法，在每一個制導周期內，通過實時優化飛行彈道以獲取最優制導律，避免了求解黎卡提方程，且對于復雜的問題具有較好的處理能力.但是該方法需要循環調用尋優算法來求解非線性規劃問題，優化迭代的計算量較大，效率較低，實際應用中具有一定的局限性.

鑒于加權函數對制導性能有著很大的影響，若加權函數可以根據不同的需求靈活設計，則能在很大程度上提高制導效果.比如，不局限于現有文獻，考慮其他更為復雜形式的加權函數，甚至在不同制導階段采用不同形式的加權函數，構造分段形式的加權函數.基于此，本文研究一類基于雙曲正切函數的加權函數，采用間接Gauss偽譜法，設計一種新型的落角約束最優制導律.該制導律在推導過程中不依賴于加權函數的具體形式，因此可以非常方便地處理復雜形式的加權函數(如分段形式)，很大程度上提高了加權函數的設計自由度.

1 相對運動方程

(1)

根據圖1中所描述的運動關系，可以得到落角坐標系內的彈目相對運動方程為

(2)

(3)

圖1 彈目相對運動幾何

根據式(3)，可得矩陣形式的彈目相對運動方程為

(4)

其中：

(5)

式中:t0為初始時刻；Sf為正定的對角矩陣，用于控制終端狀態量；Th(t)為控制能量的加權函數，該函數可以有效地改變導彈的運動軌跡及制導指令的分布.本文基于雙曲正切函數設計不同的加權函數，以實現不同的制導效果.下面給出了3種形式的加權函數，其中w,t1,ts和τσ分別為設計參數.

(6)

(7)

(8)

圖2、3分別給出了加權函數的變化曲線，其中函數Th1(t)和Th2(t)對應的設計參數的取值為w=tf/3,t1=tf/2；函數Th3(t)對應的設計參數的取值為w=tf/6,t1=tf/2,ts=tf/2,τσ=tf/6.從圖2中可以看出，函數Th1在制導初始段取值很小，但隨著時間的增加，其值不斷增大.由于式(5)中加權函數處于分母的位置，故而Th1對初始控制能量的權重最大.這種形式的加權函數將產生很小的初始過載指令，可降低末制導開始時的過載指令突變，有助于中末制導的平穩交接.Th2的變化規律與Th1正相反，即對終端控制能量的權重最大.這種形式的加權函數將產生很小的末端過載，可提供更多的過載裕量以抵抗導引末段可能存在的各種外界干擾.而Th3則兼有Th1和Th2的優點，將在導引始端和末端均產生很小的過載.此外注意到，式(8)中所示的加權函數Th3為分段函數，其綜合了雙曲正切函數以及文獻[16]中所提出的Gaussian加權函數.這種復雜形式的加權函數在現有文獻中罕有研究，也給問題的求解帶來了較大的難度.為此，本文推導了一種新型的制導律，可以非常容易地處理上述復雜的加權函數.

圖2 加權函數Th1和Th2變化曲線

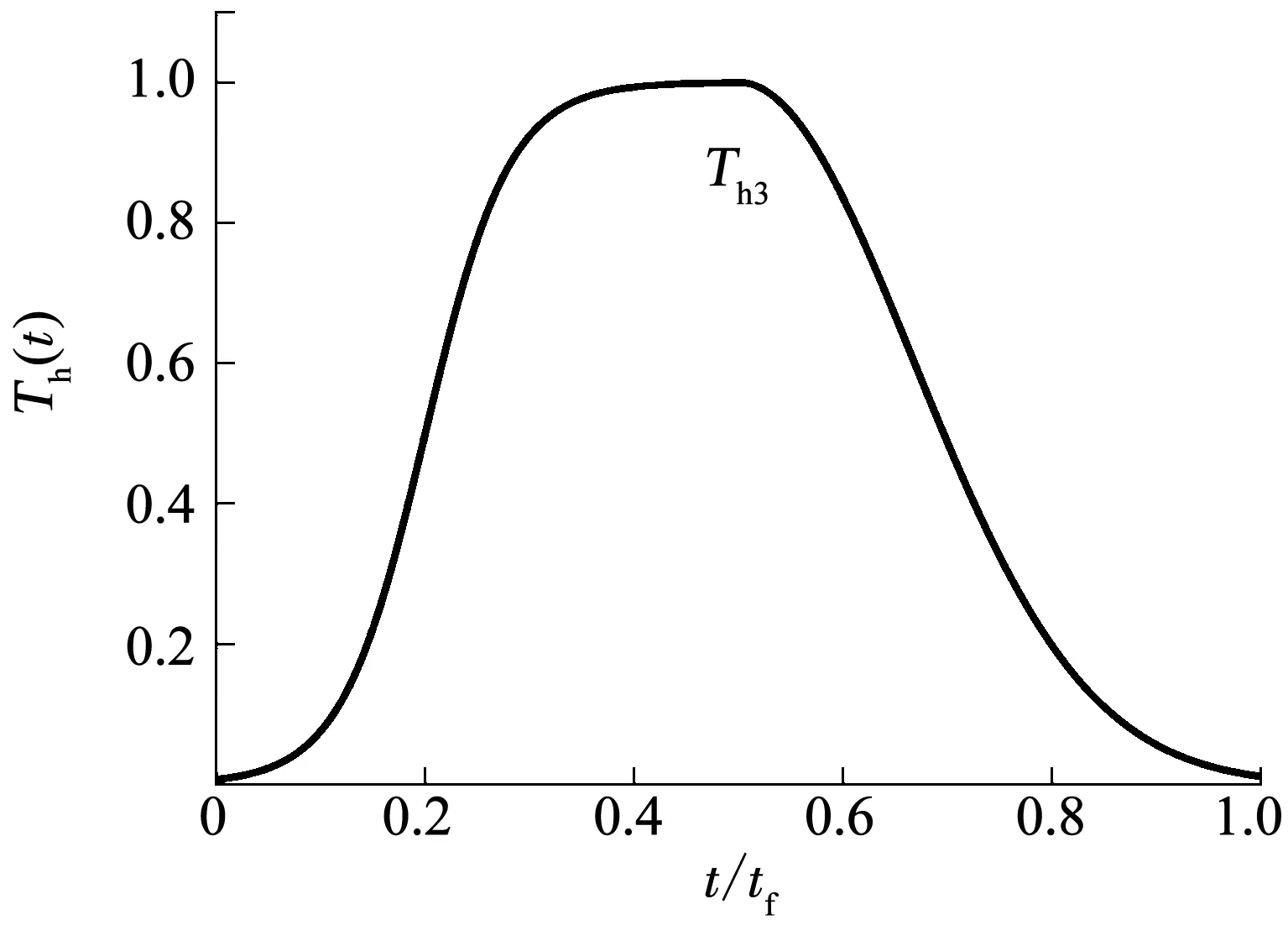
圖3 加權函數Th3變化曲線

2 最優制導律推導

由最優控制理論，可構造如下的Hamiltonian函數：

其中λ(t)為協態變量，并滿足如下的協態方程：

(9)

其橫截條件為

λ(tf)=Sfx(tf),

(10)

根據極小值原理，有

從而得到最優控制量為

(11)

將式(11)代入式(4)，并根據式(9)，可得如下的兩點邊值問題：

(12)

針對式(12)所示的帶有復雜形式加權函數Th(t)的兩點邊值問題，較難獲得解析解，這種情況下，可通過積分黎卡提微分方程來求得最優控制量，但這種方式需要大量的計算，且對于稍微復雜的系統，整個積分也變得更為困難，實際應用中限制較多.為此，本文采用間接Gauss偽譜法來求解.引入變量τ對時間t進行如下變換：

從而將區間[t0,tf]轉換為[-1,1]，故而式(12)變為

(13)

間接Gauss偽譜法的主要思想是通過構造全局插值多項式來近似x(τ)和λ(τ)，進而將兩點邊值問題(13)轉換為代數方程，求解這些代數方程即可得到最優控制量.為此，構造如下的插值多項式來近似狀態量x(τ)為

(14)

(15)

構造如下的插值多項式來近似協態量λ(τ)為

(16)

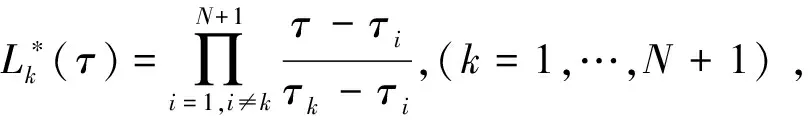
(17)

根據Gauss求積公式[22]，狀態量x(τ)的末端值x(1)可通過下式計算：

(18)

式中wk為Gauss求積系數.結合式(10)和式(18)，則協態量的末端值λ(1)可進一步表示為

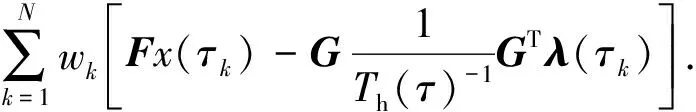
(19)

(20)

(21)

由于矩陣中D的元素可以通過下式離線計算:

(22)

其中：

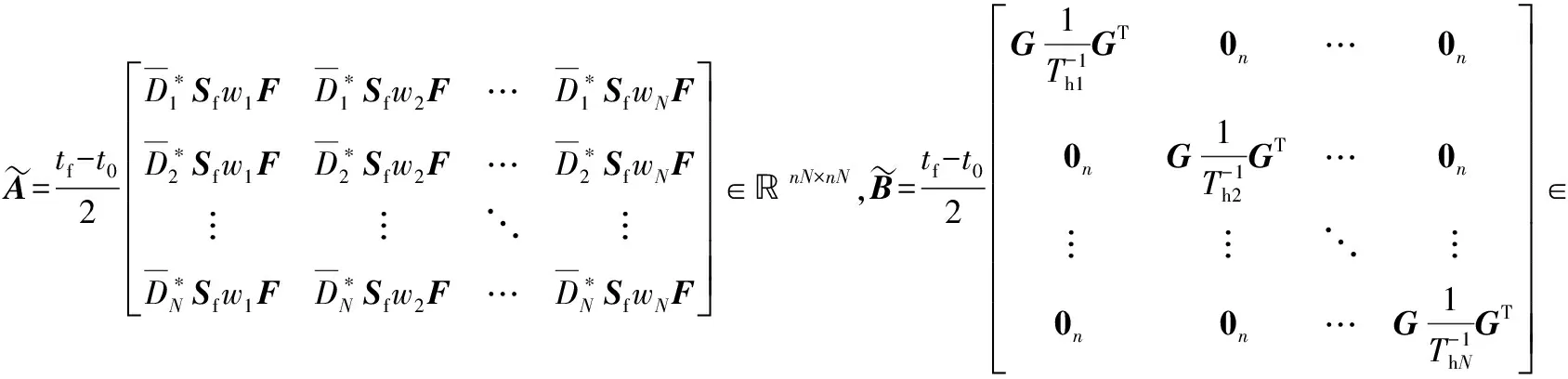
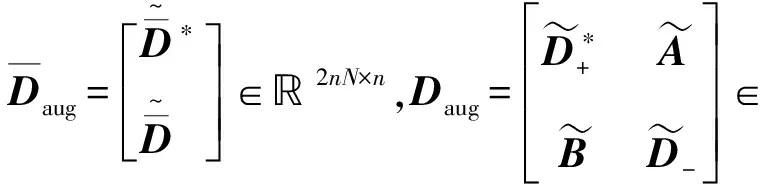
(23)

求解式(23)可得：

(24)

給定初始狀態x0，通過上式可以得到N個Gauss節點上的狀態量xi及協態量λi，i=1,…,N.由于Gauss節點并不包含邊界點，因此式(24)無法提供協態量的初值λ(-1).考慮到協態量的末端值λ(1)是已知的，因此λ(-1)可通過如下的Gauss求積公式計算得到：

至此，τ0=-1,τ1,…,τN+1節點上的協態量均已求出，根據式(11)便可得到每個離散節點上的最優控制量為

(25)

上述推導過程并未對加權函數有所限制，也不依賴加權函數的具體形式，因此，所提方法可以非常方便地處理各種復雜加權函數.此外，該方法不需要任何的積分或迭代運算，只根據初始狀態量x0即可通過式(25)方便地求出[t0,tf]區域內各節點上的最優控制量，相比于傳統反向積分黎卡提微分方程的方法，計算量小，易于工程在線計算.由于式(25)得到的是開環最優解，無法抑制外界擾動的影響.為此，采用滾動時域方法，具體步驟如下.

步驟1初始化離散節點的數量N，初始化當前時刻為初始時刻t0，給定期望落角γf.

步驟2根據目標點的位置坐標及導彈的當前位置坐標計算彈目距離R，采用公式tgo=R/Vm計算得到剩余飛行時間tgo，進而得到tf=t0+tgo.

步驟4根據式(25)計算[t0,tf]區域內各節點上的最優控制量ui(i=0,…,N+1)，只取t0時刻對應的控制量u0，并將其應用于導彈動力學模型中，計算得到下一時刻t′以及狀態量.

步驟5判斷是否命中目標.如果沒有命中目標，則將當前時刻t′作為初始時刻，即t′=t0，將當前狀態量作為初始狀態量，重復步驟2～4，直至命中目標.

3 仿真結果分析

本文通過數字仿真在不同條件下展示所提制導律的性能.在仿真中，導彈的初始位置取為(0 m,0 m)，目標的位置取為(5 000 m,0 m)，導彈速度Vm=200 m/s，導彈的初始彈道傾角γm(0)=45°；Gauss節點數N=10，Sf=diag([1×105,1×105]).為了對比說明所提制導律的效果，在同等條件下，對文獻[10]中提出的最優制導律(optimal guidance law,OGL)和文獻[24]中提出的偏置比例導引律(biased proportional navigation guidance, BPNG)也進行了仿真計算.

圖4給出了在期望落角γf=-45°條件下，不同加權函數對應的彈道曲線和制導指令變化曲線.從圖4中可以看出在不同的加權函數作用下，導彈均能滿足給定的落角約束，以期望的落角去攻擊目標.但是，不同的加權函數明顯地改變了導彈的運動軌跡以及制導指令的分布.Th1(t)在導引初始段產生了很小的制導指令，這主要是因為Th1(t)對初始控制能量的加權最大所致；這種類型的制導指令可有效降低制導律對初始狀態誤差的敏感度.由于Th2(t)的變化規律與Th1(t)相反，對末端控制能量的加權最大，因此隨著導彈趨近于目標，其對應的制導指令也趨向于零，這有助于提高制導律在導引末端的抗干擾能力，即可提供更多的過載裕量來抵抗外界干擾.而Th3(t)則在導引始端和末端均提供了很小的制導指令，因此該加權函數不僅能降低制導律對初始狀態誤差的敏感度，而且還可以提高導彈的末端抗干擾能力.由于本文算法并不依賴于加權函數的具體形式，因此在實際工程應用中，可進一步靈活設計加權函數的變化規律，以實現不同的制導要求.此外，從圖4中還可以看出，傳統的OGL雖然能夠以能量最優的方式導引導彈以期望的落角命中目標，但是其初始及末端導引指令較大.BPNG雖然也能夠保證導彈在滿足落角約束的條件下命中目標，但其在彈道末段產生了很大的過載.因此，若要滿足不同的制導需求，上述兩種方法有一定的局限性.

圖4 不同加權函數條件下的制導效果

為了進一步考察初始初始狀態誤差對制導指令的影響，圖5給出了γm(0)存在10°誤差以及ym(0)存在100 m誤差下，OGL和Th1(t)的對比仿真結果.從圖5中可以看出，當存在較大的初始狀態誤差時，傳統的OGL產生的制導指令在初始階段變化較大，而本文的制導律則可使得制導指令在初始階段始終保持很小的值，這樣的特點在中末制導的平滑交接中具有一定的優勢.

圖5 考慮初始狀態誤差的制導效果

為了進一步展示制導律在導引末端的抗干擾能力，圖6給出了末端存在陣風的情況下，OGL和Th2(t)的對比仿真結果.其中當彈目距離小于500 m時，沿ox軸正向對導彈施加25 m/s的陣風.從圖6中可以看出，兩種制導律在彈道末端均產生了額外的制導指令以抵抗陣風的干擾.由于OGL在彈道末端的需用過載較大，在附加額外的過載指令后產生了飽和現象，進而導致了接近20 m的脫靶量.而本文的制導律在彈道末端的需用過載很小，在附加額外的過載指令后仍有一定的裕量，從而很好地保證了最終的命中精度.

圖7給出了期望落角分別為-10°,-30°,-60°和-90°的條件下，加權函數Th3(t)對應的彈道曲線和制導指令變化曲線.在這4種場景下，最終落角分別為-10.026°,-30.023°,-59.988°和-90.011°，可以很好地滿足相應的落角約束.從圖7(a)可以看出，導彈在不同場景下也均能準確命中目標.從圖7(b)可以看出，在不同的落角約束情況下，加權函數Th3(t)均能保證在導引始端和末端產生很小的制導指令.上述結果表明，雖然本文制導律是基于線性化模型推導而來的，但其對較大范圍內的落角約束具有較好的適應性.

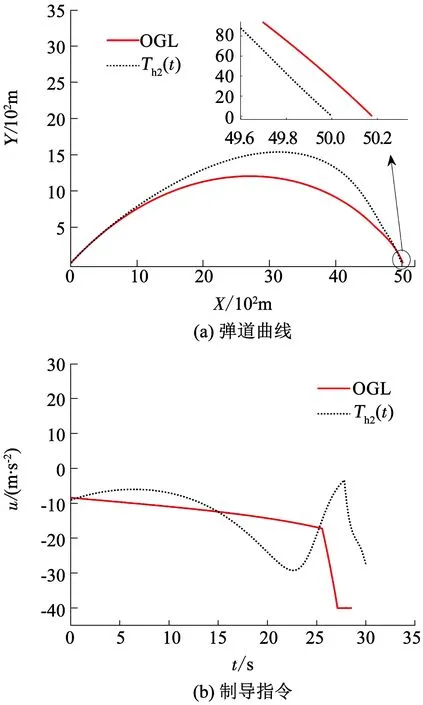
圖6 考慮末端風干擾的制導效果

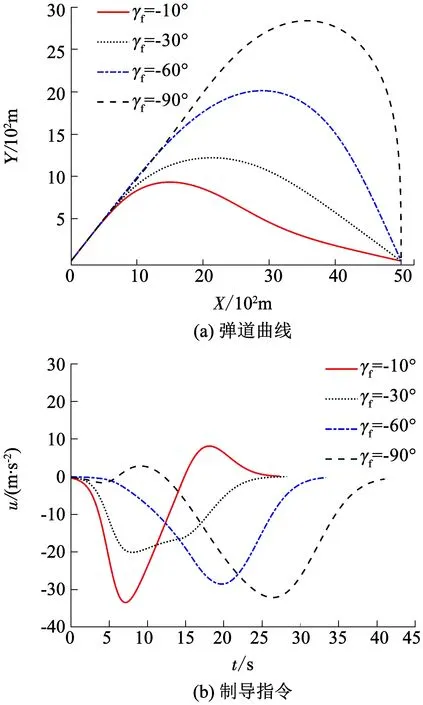
圖7 不同落角約束下Th3(t)加權函數的制導效果

Fig.7 Guidance performance forTh3(t) with different impact angle constraints

為了進一步驗證加權函數對制導效果的影響，以加權函數Th3(t)為例，選取不同的設計參數進行仿真分析.具體參數見表1，每個算例對應的加權函數Th3(t)的外形曲線如圖8所示，仿真結果如圖9所示.

表1 加權函數Th3(t)的參數取值

圖8 不同參數條件下的加權函數Th3(t)曲線

從圖8中可以看出，通過調整設計參數w,t1,ts和τσ的值，可以靈活地改變Th3(t)的外形，進而控制不同區域內控制能量的權重系數.從算例1到算例3，加權函數對導引始段和末段的控制能量的約束逐漸寬松，即要求較小的控制量在始末段內持續的時間逐漸變小.

從圖9可以看出，在3種算例下，導彈均能以期望的落角命中目標，但其運動軌跡和制導指令的分布卻有所不同.在算例1中，導引始末段內制導指令在較長時間內保持了較小的值，導引中段內指令的值則相對較大.而在算例3中，制導指令在導引開始時增長較快，這樣可使導彈更快地向目標收斂，這和圖9(a)中的彈道曲線的規律是一致的，在導引中段所需的制導指令則較小.從以上結果可以看出，通過不斷收緊導引始末段內Th3(t)的取值，有助于降低導彈對初始狀態誤差的敏感度、提高末端的抗干擾能力，但同時也提高了導引中段內導彈的過載要求.由于本文方法在推導中不依賴于加權函數的具體形式，因此在實際應用中，可針對不同的需求，靈活調整相應參數，以獲得滿意的制導效果.此外，不局限于本文所給出的幾種類型的加權函數，為了實現某些特定的制導要求，還可設計其他更為復雜的加權函數，因此，本文方法給制導律的設計帶來了很大的自由度.

圖9 Th3(t)在不同參數條件下的制導效果

Fig.9 Guidance performance forTh3(t) with different parameters

4 結 論

1)結合極小值原理和Gauss偽譜離散方法，將最優末制導問題轉換為一系列的代數方程進行求解，該方法避免了直接法中的尋優過程以及間接法中的求解黎卡提微分方程，不需要進行繁瑣的積分運算.

2)采用雙曲正切加權函數，通過合適地調整加權函數的曲線形狀，可以靈活調整不同階段控制能量的權重，進而改變導彈的飛行軌跡和制導指令分布，不僅能降低制導律對初始狀態誤差的敏感度，而且還可以提高導彈的末端抗干擾能力.

3)所提制導律在推導中不依賴于加權函數的具體形式，可非常方便地處理各種復雜形式的加權函數，如分段非光滑加權函數，為不同制導需求下設計末制導律提供了很大的自由度.