基于VAR-TARCH模型的鐵礦石期貨價格發現功能實證研究

許可 劉靜怡

摘?要：本文選取2015年5月至2020年6月國內大連商品交易所（以下簡稱“大商所”）的鐵礦石期貨市場與現貨市場為研究對象，建立不同分布假設下的VAR-TARCH模型，得出結論：兩市場之間存在波動溢出效應，價格滯后4期時趨于平穩，期貨價格和收益率的變化對于現貨市場具有警示作用。此外，正負沖擊的非對稱性也得到證明。基于以上結論，本文提出鼓勵鐵礦石資源保障體系發展、提升市場監管透明度以及完善市場機制以爭奪國際定價權等諸多建議。

關鍵詞：鐵礦石期貨?價格發現?VAR-TARCH模型

一、引言

期貨市場自創立以來，就一直與現貨市場保持著緊密的聯系。商品期貨作為期貨的“主力軍”，為實體經濟服務的同時，也為市場投資者提供獲利機會。由于現貨市場商品價格波動，商品生產經營者難以準確把握成本和利潤水平，利用期貨市場進行套期保值交易成為鎖定收益和成本的捷徑。套保者和投機者的存在是期貨市場和現貨市場之間堅固的橋梁和靈敏的媒介。期貨價格的形成與變動表面上是合約的多空力量對決，但其實質是現貨市場供求關系的體現。期貨市場具有價格發現的功能，在生產、貿易中作為商品的基準價格或參考價格的來源而備受關注。

鐵礦石指存在利用價值的，含有鐵元素或鐵化合物的礦石，在生產中主要作為鋼鐵原材料而使用。鋼鐵廣泛應用于基礎建設、房地產等社會領域，其價格對社會平均生產成本具有重要意義。因此，鐵礦石現貨價格與國民經濟血脈相連。2010年以前，由于我國鋼企生產分散、采購分散、出口集中的特點，鐵礦石交易在國際上難以掌握定價權。這一時期主要采用長期協議定價模式，鐵礦石行業“三巨頭”——力拓、必和必拓以及巴西淡水河谷公司把持世界范圍內的定價權。隨著鐵礦石三大指數的推出，賣方壟斷市場逐漸向買方壟斷轉變，指數定價的實現為衍生品市場發展提供溫床。可以預見的是，未來期貨價格必將替代指數定價，成為定價基準。

為了順應鐵礦石金融化趨勢，提升我國交易地位，2013年，大連商品交易所正式上市掛牌交易鐵礦石期貨合約。作為當時世界最大的鐵礦石消費國、進口國和第二大生產國，這一期貨品種的上市，完善了定價機制，使其有效服務于實體經濟，在本國鋼企管理現貨價格波動風險、控制生產銷售成本、參與國際市場競爭等眾多方面起到積極作用。未來鐵礦石期貨的發展有望使中國在國際大宗商品的定價權爭奪戰中占據主導地位。中國市場上鐵礦石的期貨與現貨價格對世界市場產生的影響正在不斷增強，通過信息溢出傳導到各大交易市場，作用于諸多行業。

本文選取國內鐵礦石期貨市場與現貨市場作為研究對象，篩選2015年5月至2020年6月期貨合約報價及現貨鐵礦石綜合指數的有效數據，計算對數收益率，并分別對價格和收益率兩種時間序列數據建立GARCH族模型，研究模型存在的波動聚集效應及信息溢出效應，長短期均衡及因果影響，通過脈沖響應與方差分解等計量方法探索目前期貨市場定價的有效性和顯著性。

本文的主要貢獻在于兩方面：一是通過研究期貨價格發現的特征，明晰鐵礦石現貨與期貨價格的影響關系，有助于投資者更有效地實現套利和套期保值;二是通過模型的建立及檢驗，發現定價機制中存在的不足，提出對監管完善市場具有啟示作用的建議。本文的創新之處有兩點：一是對收益率進行研究而非停留在期貨價格與現貨價格的層面上，二是采用不同分布假設下的非對稱GARCH模型進行擬合，結合VAR模型的脈沖響應與方差分析，更準確的刻畫價格的波動特征。

二、研究背景與文獻綜述

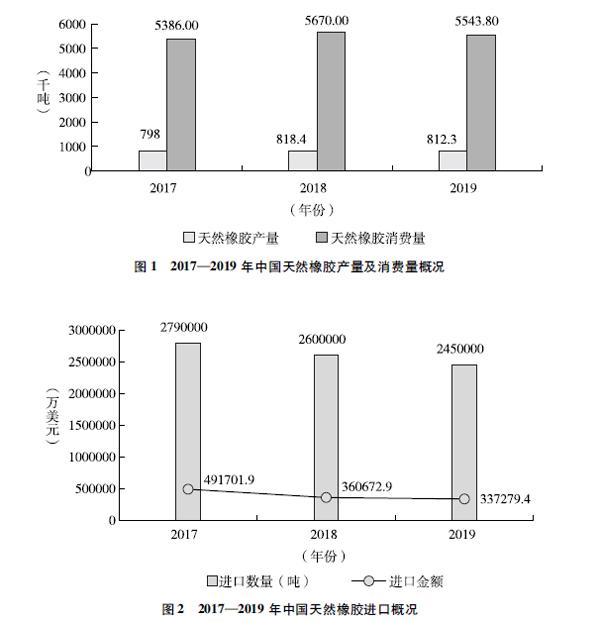
鋼鐵作為國民經濟的重要支柱性產業，對制造業的發展舉足輕重。我國鐵礦儲量豐富，已探明的鐵礦總數達600億噸，每年鋼鐵產量約占全球的53%，是名副其實的礦產大國。但是由于礦產含量、地理位置和開采技術等，目前自身開采的鐵礦石產量不能滿足日益增長的需求，較低的品質也限制了其在高精技術行業的使用。據中鐵網統計，2019年鐵礦石累計產量是84，4356萬噸，同期進口的鐵礦石就達到107億噸，相當于我國鐵礦石的進口依賴度達到56%左右，主要從澳大利亞、巴西、印度等國進口。

與大多數商品期貨類似，影響鐵礦石價格的主要因素是供求關系。供給方面一般分為成本因素、產量因素、庫存三方面，其中，成本主要包括礦山的開采成本、人工成本、稅費及運輸費用;產量因素則是指礦山企業產能的變化情況;庫存產生的影響則是由各地區存量與貿易商策略共同決定。需求方面主要來源于市場上鋼企的需求、替代產品和互補品的價格變化等。除此之外，政策以及國際貿易是同時作用于鐵礦石交易的供需兩端，影響原理和機制也較為復雜，是目前學界研究的重點。閆麗娜（2009）結合制度經濟學與國家安全理論，使用對比分析法提出應對鐵礦石價格上漲的宏觀經濟對策。徐斌（2016）基于Goldberg和Knetter的剩余需求彈性模型，研究發現巴西、澳大利亞、印度在中國鐵礦石市場具有勢力，并從期貨市場出發給出提高我國鐵礦石國際定價權的對策建議。中國在全球鐵礦石交易中的地位有助于推動市場壟斷和金融化，造成鐵礦石國際貿易價格的短期波動（陶建格等，2018）。

2013年大商所推出鐵礦石期貨，標志著中國將在鐵礦石交易中采取主動態度，爭取國際話語權。該合約是全球首個采用實物交割方式履約的合約。沈寧（2013）認為，實物交割的方式能更直接地向實體經濟提供服務，從而吸引國外企業投資我國期貨市場。學界有關國際定價權的研究主要可以概括為以下三方面：一是議價能力。Baillie（2002）通過建模發現本國的大宗商品議價能力可以通過定價權實現。國內學者劉慶柏（2009）運用GARCH模型檢驗發現期貨市場的價格發現功能能有效提升中國在國際交易中的定價地位。二是市場開放程度。隨著金融市場的逐步開放，建立國際性的鐵礦石期貨市場對把握定價權具有重要意義（張艷飛等，2013）。楊愛紅（2013）也持此觀點。三是國際影響力。鄧超、袁倩（2016）對鐵礦石、螺紋鋼以及荷蘭的普氏指數建立VAR模型，并得出我國鐵礦石期貨國際影響力逐年增強的結論。

定價權的實現離不開期貨市場的發展，期貨市場定價功能的完善能夠補充現貨市場波動性帶來的缺陷。本文主要研究期現貨兩市場間價格在信息傳遞過程中的波動溢出效應，兩種價格傳導的效率體現市場的投機水平，投機水平的高低直接反映期貨市場的完善程度。目前國內學界對于波動溢出效應的研究可以分為以下三方面：一是長短期均衡。李瓊（2013）借助Johansen協整模型對鐵礦石的期貨價格與現貨價格進行研究，發現二者之間存在長期均衡關系。此外，也有學者使用VEC-SVAR模型擬合，得出國內外鐵礦石期現貨價格之間存在高度相關性和長期均衡關系（胡振華等，2018）。二是價格的引導與發現。鐘國新等（2015）通過實證研究發現鐵礦石國際市場的期貨價格對現貨價格具有顯著正效應，從而表明其具有價格發現功能。雷元安等（2019）采用時間序列檢驗法對近6年的數據進行實證研究，發現期貨價格對現貨價格的影響貢獻度為7704%。三是不同市場間的類比。國內學者進行了諸多期現貨市場的比較：劉文文、喬高秀（2014）針對股指期貨的波動溢出效應進行研究，發現兩市場信息反映的速度之間存在差異。有學者使用雙變量EGARCH模型、GarbadeSilber模型對原油期貨市場價格發現功能進行分析，得出兩價格協整關系和格蘭杰因果關系的結論，證明了波動溢出效應（董瑩、李素梅，2017）。

由于波動溢出效應的存在，國內外學者對期現貨價格及收益率的研究一般使用GARCH族模型，并與其他模型組合使用。彭紅楓和陳奕（2015）在銅期貨套期保值比率的計算中建立了MRS-DCC-GARCH模型，該模型能夠有效消除GARCH模型帶來的波動率的高持續性。采用Ling和McAleer（2003）提出的VARMA-GARCH模型，李保林等（2015）研究我國滬深300股指期貨2012—2014年1分鐘高頻交易數據，檢驗證明了兩市場之間的波動溢出效應。Haigh和Holt（2002）建立BEKK-GARCH模型針對外匯期貨交易進行研究，在商品期貨套利方面做出重要貢獻。在以上研究的基礎上，本文采用非對稱TGARCH模型對我國鐵礦石期現貨市場價格指標及收益率序列進行擬合，以期發現兩者之間的因果作用關系、波動方式的差別以及定價機制的有效性，從而幫助投資者進行策略選擇。

三、模型設定及實證分析

1模型設定

研究表明，金融時間序列波動主要具有三大特征，即尖峰厚尾分布、波動聚集以及長期相關性。基于此，本文采用GARCH族模型擬合。普通的GARCH（1，1）模型一般形式如下：

其中，式（1）是模型的條件均值方程，與一般最小二乘回歸方程類似;式（2）是ε隨機誤差的條件方差方程，αε2t-1為ARCH項，βσ2t-1為GARCH項。該模型的參數可以替換為GARCH（?q，?p?），此時（1）式不變，（2）式變為：

當q=0?時，模型可簡化為ARCH（?p?）。模型中，ω為原有的不確定性，是殘差的長期均值;方差滯后項為歷史信息帶來的波動影響;隨機誤差滯后項為近期市場出現的新沖擊對方差的影響，一定程度上代表了信息傳遞效率的高低。

按照分布假設不同，可以將模型分為正態分布的N-GARCH、students?t的廣義t-GARCH（Bollerslev，?1987）以及廣義誤差分布的GED-GARCH（Nelson，?1991）。此外，Engle、Lilien?&?Robins于1987年提出針對不同的變量分布時的GARCH-in-Mean模型，可以將在均值方程中加入方差的其他形式，包括以下三種：

除此之外，本文選取的金融時間序列中有異常值存在即尖峰厚尾現象，為了貼合數據的分布特點，本文嘗試T分布、GED分布下非對稱模型TGARCH的擬合，選取信息準則值最低和顯著性最高的模型作為最終結論。

2數據處理

本文選取2015年5月至2020年6月大連商品交易所鐵礦石連續交易日的期貨收盤價及中國鋼鐵業協會統計的鐵礦石現貨綜合價格指數分別作為期現貨市場的價格序列，數據來自Wind金融終端及中鋼協官網。篩去非交易日及特殊事件停盤日期，共得1234條數據。為增加序列的平穩性，同時盡量保持計算的精度和準確度不受影響，本文的收益率序列采用對數收益率，計算公式如下：

其中，i=f或s，f表示期貨，s表示現貨。Pi，t以及Pi，t-1為在t時刻的收盤價，ri，t為在t時刻百分比化的對數收益率。

3數據描述性統計

預處理結束后，本文得到四條時間序列：期貨價格、現貨價格、期貨對數收益率以及現貨對數收益率，下文建模中分別采用Ft、St、rf，t和rs，t表示。為描述數據在不同時間上的波動情況，首先對序列進行統計分析：

由表1可知，期貨價格整體低于現貨價格，但波動區間更大，標準差也相應地大于現貨價格。從分布上看，期貨價格的峰度較現貨價格高，且高于臨界值3，說明其分布為統計學上典型的尖峰厚尾，這也是金融時間序列的特點。Jarque-Bera統計量表明，樣本均不服從正態分布。類似的，表2揭示了期貨收益率與現貨收益率之間的統計關系：期貨收益率波動幅度更大，厚尾的程度更重，且兩者同時不服從正態分布。更直觀地從時序圖上來看，價格方面（圖1），期貨價格更易出現異常值，短時間內上下波動概率更高，合理分析其存在ARCH效應;收益率方面（圖2），針狀曲線的出現佐證了波動從聚性存在的推論，且直觀上收益率序列的波動程度高于價格序列。兩者之間的具體聯系還需進一步檢驗。

根據恩格爾和克拉格（1983）年對宏觀時間序列的研究結果，擾動方差的穩定性更差，方差的大小隨時間變化，具有某種相關性，并據此提出了ARCH效應。該效應的存在使得建立GARCH模型成為可能，但GARCH模型的建立必須要求序列具有平穩性，因此在建模前首先需要對數據進行平穩性檢驗。Augmented?Dickey-Fuller?Test（ADF）是單位根檢驗的一種方法，存在以下三種形式：

其中，式（7）為普通形式，式（8）為存在截距項，式（9）為存在截距項和斜率項。本文對原序列進行普通形式的檢驗后，若不平穩，則繼續使用截距項形式對相應的一階差分序列檢驗，得到結果如表3所示。

ADF采用一階自回歸假設，對隨機干擾項的方差即白噪聲在時間上的變化進行檢驗，得到單個序列的平穩性結論。P值小于置信水平意味著對原假設H0的拒絕，即不存在單位根。對本文數據檢驗發現，以P值為判斷依據，價格序列本身不平穩但其一階差分序列平穩;收益率序列本身平穩。由此，價格序列具有一階單整的性質，收益率序列本身為平穩序列，一定程度上避免了造成GARCH模型“偽回歸”的情況。

除了非平穩的過度擬合，“偽回歸”還存在一種特殊情況，即兩時間序列的趨勢成分相同，共同趨勢的修正原有較弱的解釋力度，導致回歸的置信水平提高。現實中的時間序列通常為非平穩序列，修正方法主要有兩種：一是如上文所述取其差分變為平穩，但會失去一些原有信息，甚至可能導致經濟學意義的偏差;另一種則是通過協整解決問題。金融時間序列理論中存在長期相關性假設，即歷史事件會在價格中持續反映。協整關系揭示序列的長期均衡水平，若原序列不平穩，一階差分平穩，但原序列存在協整關系，則同階情況下（如一階單整）可以對原序列建立VAR模型，進行脈沖響應和方差分解。

協整檢驗結果如表5所示。對價格模型而言，原假設為協整關系個數為0時，跡統計量?為3001863，拒絕原假設;原假設協整關系個數為1時，跡統計量為0756733，P值為03844，接受原假設，期貨價格與現貨價格之間存在協整關系。收益率模型的檢驗結果表明協整關系不存在。綜上，對價格建立VAR模型如下：

價格的一階差分序列與收益率序列均具有平穩特征，檢驗波動聚集效應后即可建立GARCH模型。一般而言，在金融模型中，由于變量滯后性、時間慣性以及其他隨機誤差的影響，時間序列常常會存在自相關和偏相關性。取36階的自相關Q-Statistic（見表5），可以得出四時間序列均存在ARCH特征，表明信息借助于期現貨資產的價格波動在兩市場間傳遞。

在此基礎上，本文對一階差分價格序列以及收益率序列分別進行OLS回歸并檢驗ARCH異方差的存在，得到的P值均小于005且nR2≥χ2分布下置信度為95%的臨界值599，因此時間序列均顯著存在ARCH異方差，可以進行GARCH族建模。

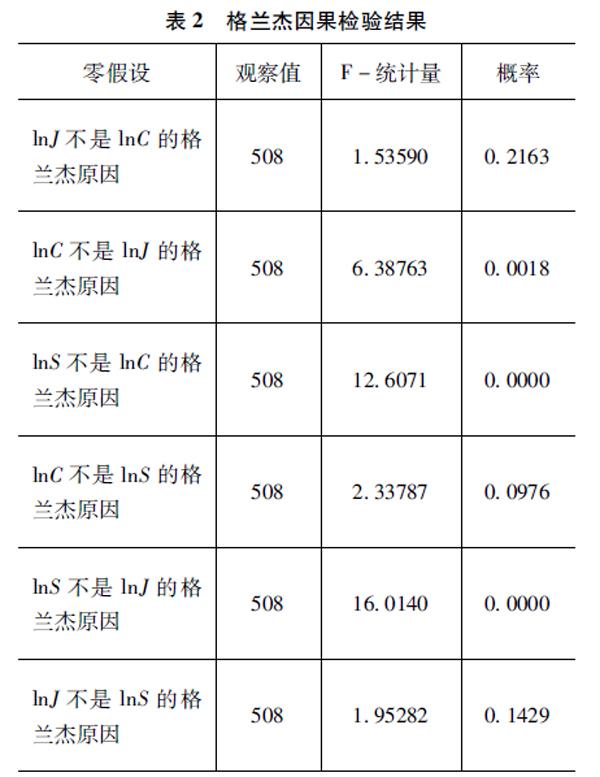
為厘清期現貨市場之間的價格和收益率的引導關系，分別對兩模型進行Granger因果檢驗。由于該檢驗需要模型的滯后階數作為參數，故先使用ARDL模型對現有時間序列的條件均值方程進行擬合，自動選擇下的結果中Selected?Model即為合適的滯后階數。由表6可知，價格一階差分模型的最優滯后階數為4階，收益率模型的最優滯后階數為1階。擬合后D-W統計量均在2附近，表明模型幾乎已無自相關性。

確定滯后階數后對變量進行格蘭杰因果檢驗，結果如表7所示。在檢驗期貨價格一階差分是否是現貨價格一階差分的Granger原因時，F值為730506，P值為200E-55;而當反向驗證時，F值為180064，P值為01263。這表明期貨價格變化可以解釋現貨價格的變化。類似的，由收益率模型的Granger檢驗可知，現貨收益率對期貨無解釋力度，期貨收益率卻可以解釋現貨收益率。綜上，期貨市場對現貨市場具有單向引導作用。

4實證分析

基于以上檢驗，本文對期現貨價格一階差分序列組合與收益率組合分別建立GARCH族模型。考慮到正負面消息對于金融市場不同程度的沖擊作用，本文以Glosten，?Jaganathan?和Runkle（1993）提出的非對稱TARCH模型為基準，借鑒吳振信等（2016）的研究，嘗試比較不同分布下的擬合，選擇信息準則最優、顯著性最高的模型作為研究結論。TARCH模型中條件方差方程中添加了非對稱項，變為下式：

其中，當t期殘差項小于0時，表示杠桿效應的滯后項參數啞變量I-t-k=1，否則為0。加入非對稱項的原因在于負面消息的沖擊一般高于正面消息的影響。基于以往的研究結果，GARCH族模型中的ARCH項與GARCH項的滯后項系數取1階即Threshold?order?=?1時，該模型能較準確地刻畫出金融市場之間的波動溢出效應。

在研究金融問題尤其是收益率時間序列時，一般取3階以下的GARCH模型參數。本文延續現有研究成果，基于不同分布假設對鐵礦石期現貨價格和波動率建立模型，得到結果如表8所示：

比較表8和表9中t分布與GED分布下的擬合結果，可以得出如下結論：以信息準則為第一判斷原則，置信度t為輔助原則，TARCH（?1，?1，?1?）最為貼合現有數據。模型表達式為：

綜上，在兩模型中，非對稱項的系數與2階ARCH項的系數均為負值，前者說明現貨市場對于期貨市場的非對稱影響是使得期貨市場的波動越來越小。結合之前表中的顯著性系數來看，在價格模型中，Threshold項系數的顯著程度t值為-6665853，P值為00000，說明價格的杠桿效應十分明顯，這也是價格波動性差異的主要來源。收益率模型中Threshold項系數的顯著程度t值為-4757921，P值也為00000，說明兩市場的非對稱性程度差距不大，兩市場上的投資者對于正負消息的沖擊所作出的反應也大致相同。這一點可以從下文中對價格本身VAR模型的分析中得到印證。

5模型檢驗

為了確認TARCH模型已完全提取了殘差中的波動效應，本文對已建立的模型進行ARCH-LM檢驗，從高階逐步遞減，檢驗結果如表12所示。

檢驗結果發現，即使是在回歸階數為1的情形下，殘差的相伴概率P值仍大于臨界值，因此在顯著性為95%的情況下接受原假設，即此時不再存在ARCH效應，模型較為合理。

對價格建立的VAR模型進行脈沖響應和方差分解，得到結果如圖3所示。

脈沖響應中，橫軸表示沖擊作用的滯后期間數，縱軸表示被解釋變量的變化，中線為脈沖響應函數，其他為正負2倍標準差偏離帶。期貨價格本身受到沖擊會隨著時間逐漸減弱，受到現貨價格沖擊則會隨著時間逐漸增強最后趨于平穩，二者的影響幅度均較小;現貨價格本身的沖擊會在第四期達到高潮并逐漸平穩，受到期貨價格沖擊則正向增強，增強的幅度先大后小、逐漸減弱。比較分析可知，與格蘭杰因果檢驗的結論一致，現貨價格對期貨價格的影響要遠遠弱于期貨對現貨的影響。

方差分解結果表明：對于期貨價格，幾乎全部的影響因素都來源于它本身，現貨價格并不能產生顯著影響;對于現貨價格，兩市場價格沖擊的貢獻率幾近相同，各占50%左右。這與之前期貨價格能影響現貨價格的結論并不矛盾。

四、結論及建議

基于對2015—2020年鐵礦石期貨與現貨市場價格及收益率的實證研究，本文分析了兩個市場間的因果關系、信息傳導的波動溢出效應以及外部沖擊帶來的影響。首先，從期貨市場與現貨市場的互相作用來看，無論是價格還是收益率方面，我國期貨市場的作用都強于現貨市場。期貨市場的波動幅度更大，這意味著鐵礦石期貨比現貨更具價格發現功能。鐵礦石作為支柱性產業的基石，其定價對于各行各業都具有重要的參考意義。期貨價格更完善的反映出市場供需在時間維度上的量及趨勢，期貨市場對于現貨市場的解釋力度使得投資者的套期保值交易和套利行為成為可能。由本文研究可得出結論：滯后4期時兩市場才趨于平穩，故期貨價格和收益率的變化對于現貨市場具有警示作用。

其次，價格一階差分序列及收益率序列均具有ARCH效應，且波動溢出效果較強。從現實意義來看，一方面，這種波動的連續性是由于兩市場之間的信息傳遞不夠及時和透明，導致投資者本該獲得的套利效果減弱;另一方面，投機行為的存在使得短期內的“新信息”和歷史的“舊信息”同時作用于市場，直接導致ARCH效應和GARCH效應的出現。雖然滯后項系數為負即波動影響逐期遞減，但以上兩種效應的存在仍然為鐵礦石的合理定價造成阻礙。定價的合理性受到削弱，對我國在鐵礦石領域爭奪國際話語權和定價權也會形成阻礙。

最后，與過往研究類似，本文所建立的TARCH模型非對稱性的來源主要是正負消息對市場沖擊的效果不同這一現象。模型顯示，針對價格波動的負沖擊尤其是期貨市場對于現貨市場的消息影響高于正沖擊這一點具有顯著性，而收益率波動差距不大。這一缺陷可能是由于本文對收益率取對數序列所致，因此也值得進行進一步的定量分析研究，模型仍然存在改進余地。但定性而言，鐵礦石價格的定價和傳導機制并未完全疏通，現貨價格對期貨的解釋程度不夠高，意味著市場投機情緒較濃，沒有很好反映供給與需求之間的關系。

依據以上研究結論，本文從政策選擇、監管與投資者保護以及市場完善與國際接軌三方面提出如下建議。

第一，鼓勵鐵礦石資源保障體系發展，優化雙焦環保政策。價格體系的構建不僅要注重上層建筑即期貨等衍生品，更要重視市場基本面的供求平衡。回顧2019年，鐵礦石的基本面具有較大剛性缺口，供應的矛盾很難在短時間內得到彌補。一方面，應當針對鋼企及上下游企業推行鼓勵政策，保障資源長久發展;另一方面，應當控制進出口鐵礦石數量，維持良好的價格生態環境。日前，鐵礦石新規即調整鐵礦石檢驗方式頒布并實施。這一規定旨在提高我國鐵礦石的質量，惠及進口交易雙方，有助于維持平衡的供需水平，也有助于提升我國的國際地位，樹立大國形象，對定價權的爭奪百利而無一害。

第二，提升市場信息透明度，保證信息公開完整傳遞。信息在兩個市場間的傳遞效果有賴于監管者的職能履行。目前鐵礦石市場存在波動溢出現象，這一現象導致了價格慣性的出現，降低了市場的有效性，為投機行為提供了溫床。監管者在價格傳遞的過程中應當全方位的監控信息公開披露的過程，及時、準確地把信息傳遞給投資者，以期幫助他們作出正確的投資選擇。監管與投資這種良性互動的存在，會使得市場的無效波動減少，更有利于實現準確定價，解決現貨對期貨市場無解釋力度的問題。

第三，完善市場機制，爭取國際鐵礦石市場定價權。期貨市場發揮價格發現的功能離不開有效市場的實現。我國鐵礦石期貨上線較晚，在國際大宗交易中雖然作為主要對手方，但并不具備主場優勢。國際定價權的爭奪有賴于國內市場率先實現定價機制的完善，合理有效的價格更易被世界市場采納。因此，鐵礦石期貨市場作為衍生品工具的重要市場，其完善在大宗商品交易浪潮中扮演著重要的角色，應當為鐵礦石現貨定價做出積極貢獻。雄厚的現貨基礎、成熟的期貨市場的良性期現互動，能增強價格的權威性，使中國在國際定價發展中掌握主動權。

參考文獻

[1]閆麗娜?我國應對鐵礦石價格波動的宏觀對策研究[D].北京：中國地質大學，2009

[2]徐斌國際鐵礦石貿易市場勢力測度分析[J].經濟問題探索，2016（10）：73-79

[3]陶建格，沈鐳，劉長虎，何利，張肅中國鐵礦石進口供需形勢與邊際定價研究[J].中原工學院學報，2018，29（02）：73-81

[4]沈寧?鋼鐵行業艱難弱復蘇?金融化大潮帶來產業鏈變革[N].?證券時報，2013-10-25（A15）.

[5]Richard?T?Baillie，G?Geoffrey?Booth，Yiuman?Tse，Tatyana?Zabotina?Price?discovery?and?common?factor?models[J].?Journal?of?Financial?Markets，2002，5（3）.

[6]?劉慶柏?我國大宗商品國際定價權研究[D].?南京：?南京財經大學，?2010

[7]?張艷飛，王高尚，陳其慎，宋科余我國鐵礦石期貨市場未來趨勢淺析[J].中國礦業，2013，22（11）：9-12

[8]楊愛紅?基于定價權的我國鐵礦石期貨市場探析[J].?金融市場，?2011，（2）：70-72

[9]鄧超，袁倩基于VAR模型的鐵礦石國際定價權研究[J].統計與決策，2016（09）：162-164

[10]李瓊?國際鐵礦石期貨價格與現貨價格關系研究[D].山東：中國海洋大學，2013

[11]胡振華，鐘代立，王歡芳中國鐵礦石期貨市場的定價影響力研究——基于VEC-SVAR模型的實證分析[J].中國管理科學，2018，26（02）：96-106

[12]鐘國新，龐立讓，孔東民鐵礦石期貨的價格發現功能研究[J].江漢學術，2015，34（05）：89-95

[13]雷元安，刁節文我國鐵礦石期貨價格發現功能的實證研究[J].經濟研究導刊，2019（36）：67-68

[14]劉文文，喬高秀我國股指期貨市場價格發現功能和波動溢出效應研究——基于VECM-DCC-MVGARCH模型[J].武漢金融，2014（08）：17-22

[15]董瑩，李素梅我國石油期貨市場價格發現功能及波動溢出效應研究[J].價格月刊，2017（07）：19-24

[16]彭紅楓，陳奕中國銅期貨市場最優套期保值比率估計——基于馬爾科夫區制轉移GARCH模型[J].中國管理科學，2015，23（05）：14-22

[17]Shiqing?Ling，?Michael?McAleer?On?Adaptive?Estimation?in?Nonstationary?ARMA?Models?with?GARCH?Errors?2003，?31（2）：642-674

[18]李保林，阿布都瓦力·艾百我國股票期現貨市場間的溢出效應研究——基于1分鐘高頻數據的實證檢驗[J].金融發展研究，2015（05）：3-9

[19]Michael?S?Haigh，Matthew?T?Holt?Hedging?foreign?currency，?freight，?and?commodity?futures?portfolios—A?note[J].?Journal?of?Futures?Markets，2002，22（12）.

[20]吳振信，萬埠磊，王書平基于不同分布EGARCH模型的EUETS價格波動和風險研究[J].數學的實踐與認識，2016，24，8-?14