基于L系統的水稻根系建模與可視化①

彭 英,張素蘭

1(德宏師范高等專科學校 經濟與管理學院,芒市 678400)

2(長江師范學院 大數據與智能工程學院,重慶 408100)

3(長江師范學院 三峽庫區環境監測與災害防治工程研究中心,重慶 408100)

4(昆士蘭大學 園藝科學中心,布里斯班 4072)

隨著世界人口的日益增長,糧食供應需求不斷增加,提高植物水分與養分利用效率則成為一項大挑戰.植物生產力受諸多環境因素制約,如輻射攔截、土壤中水分與養分供給等,因此必須對植物生長關鍵過程進行較為深入的了解,以便在有限的資源環境中改進行植物種植方法和改良植物品種[1].為了實現植物的可持續生產,特別是在土壤肥力減少、潛在短缺、成本增加、氣候變化、干旱頻繁增加的情況下,了解植物根際與根際性狀對植物資源效率的影響尤為重要[2].因此植物根系是結構是影響植物生產力的一個基本方面,在植物生長過程模型中需要精確描述[3].

近年來,國內外學者在植物根系生長模擬方面進行了較為深入的研究[4-8].Pagès 等[9]提出RootTyp 模型,該模型依據觀察所得根系結構特征,形式化定義了不同根類別及其生長率、向性、分枝等特征模擬根系結構.Postma 等[10]構建OpenSimRoot 模型,用于模擬根系結構、養分獲取和植物生長,并成功應用于玉米根系生長過程模擬.在國內,吳劼[11]開發一整套用于測定田間成熟玉米根系結構的方法,用于田間玉米根系三維結構的測定與可視化仿真.胡軍成等[12]依據根系生長發育的基本結構單元,利用根系與地上部葉片生長之間的同伸關系,以生長度日為時間尺度,建立小麥初生根、節根與分枝根發生過程的動態模型.李松陽等[13]基于L 系統研究了群體行為對根系生長的影響.

由于水稻根系沒有突出的生長特征等,同時較其它植物如小麥、玉米更為復雜,因此定量化水稻根系的結構比較困難[14].目前,國內外學者已對水稻根系做了比較深入的研究,但大多側重于水稻根系形態、生理機能、根系與地上部的關系以及栽培管理措施對水稻根系的影響等[15-17],而在研究根系三維建模與可視化方面的成果并不多見.本文在L 系統[18]的基礎上,分析了水稻根系生長特性,定義了水稻根系的生長方向、生長及分枝規則、對水稻根系進行建模,并利用L-studio 工具[19]實現了重力指數及偏轉指數控制下水稻根系生長過程的動態模擬.

1 L 系統

L 系統[20]是由Prusinkiewicz、Lindenmayer 等提出的形式化描述植物生長過程與形態變化的方法.之后Prusinkiewicz 等[21,22]對L 系統進行了長期深入的研究,他們提出了參數L 系統、隨機L 系統、上下文相關L 系統等,使得L 系統成為目前應用較為廣泛的一種虛擬植物建模工具.L 系統是一個模式字符串的替換過程,其核心概念是重寫機制.通過對初始模式字符串應用產生式規則,進行有限次迭代生成當前模式字符串,然后再將模式字符串解釋成復雜的幾何圖形并在計算機上展示出來.

1.1 L 系統定義

假定V表示字母表由模式字符串的集合構成,V*表示字母表V中所有模式字符串構成的集合即V的閉包,V+表示字母表中所有模式字符串構成的非空集合即V的正閉包,則L 系統可形式化定義為一個有序三元組:

其中,ω∈V+表示非空模式字符串集合即公理,P∈V×V*則表示產生式的集合.P中產生式通常表示為S→χ,其中,S∈V稱為產生式的前驅,χ∈V*稱為產生式的后繼,→表示前驅在迭代過程中將會被后繼替代.對于V中的任意一個模式字符串S,至少存在一個后續模式字符串集合χ,滿足產生式S→χ,如不存在則假定其后繼為其自身即S→S.

1.2 L 系統圖形解釋

在L 系統中公理和產生式均由模式字符串集合構成,經過迭代演化所得到的結果也是模式字符串集合.為使L 系統迭代演化所生成的模式字符串集合能夠映射成某種圖形,要為L 系統中每個模式字符串賦予特定的圖形含義,我們把這個由模式字符串向圖形的映射過程稱為L 系統的圖形解釋.根據文獻[23]介紹,Szilard等在1979年提出了“龜圖形幾何(Turtle geometry)”的概念,通過對模式字符串進行龜圖解釋來表示復雜圖形,后來Prusinkiewicz 和Hanan 對其進行了擴展,使得Turtle 解釋成為L 系統最常用的圖形解釋工具.

2 水稻根系建模

水稻為須根系植物,其根系由種子根與不定根組成[24,25].種子根只有一條,由胚根生長而成.不定根又稱節根,由莖基部若干不伸長的節上發生.隨著葉片的抽出,不定根按發根節位由下而上漸次分化發生.種子根和不定根可發生一次分枝根,一次分枝根上可發生二次分枝根.高產條件下可發生五、六次分枝根,形成強大而密集的根群.我們用帶有參數的模式字符串T表示根尖,B表示產生分枝的結點,S表示種子根發根結點,N表示不定根的發根結點.則模式字符串T、B、S、N和Turtle 命令一起構成了水稻根系L 系統模型中的模式字符串集合即V.

2.1 單根生長方向建模

在單位時間步長內,根尖新生長方向取決于前單位時間步長內的原生長方向,相對原生長方向的軸向偏轉角度和徑向偏轉角度,我們分別用α和β表示,如圖1所示.新的根段生長方向與原生長方向成一定角度且徑向隨機偏轉.

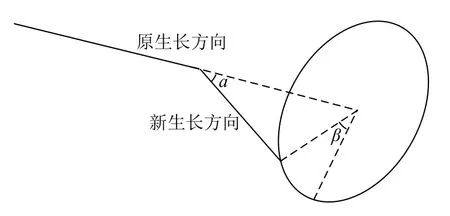
圖1 根尖生長方向偏轉

軸向偏轉角度α表示重力影響下根尖偏轉方向,模型中其值取決于重力指數G[26],我們用式(2)描述軸向偏轉角度α與重力指數G之間關系.

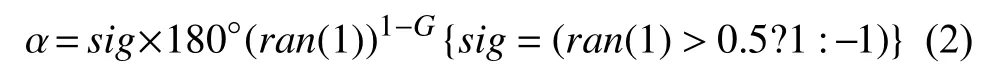
其中,ran(1)表示取[0,1]之間隨機值的函數.重力指數G取值范圍為[0,1].當重力指數G為0 時,表示軸向偏轉角α在[-180,180]范圍內取隨機值,重力指數G越接近1,表示偏轉角α受重力影響越大.我們用Turtle 命令Down(α)表示軸向偏轉操作.

同理,徑向偏轉角β表示圍繞原根尖方向偏轉角度,模型中其值取決于偏轉指數D[26],我們用式(3)描述徑向偏轉角度與偏轉指數D之間關系.

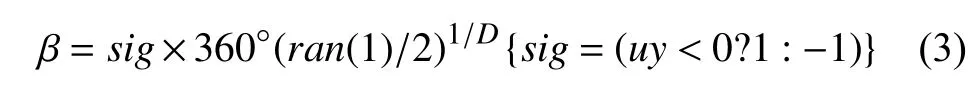
其中,uy表示Turtle 坐標系中向上方向向量的y值.同樣,偏轉指數D取值范圍為[0 1],當偏轉指數D接近0 時,表示在徑向方向幾乎沒有偏轉.當偏轉指數D逐漸增大至1 時,徑向偏轉角度完全隨機生成.我們用Turtle 命令RollL(θ)表示徑向偏轉操作.

2.2 單根生長及分枝建模

在單位時間步長內水稻根系生長主要由根尖分生區伸長實現,分枝則由分枝區產生,單根生長及分枝產生式可用式(4)描述.

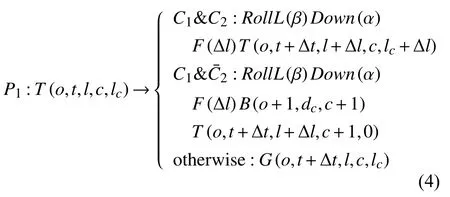
參數o表示單根所處的分枝層次,t表示單根生長時間,l表示單根當前長度,c表示單根上產生的分枝數目,lc表示當前位置距第c個分枝的長度.條件C1及C1分別定義為:C1={l+Δl＜lmax}判斷當前根的長度是否小于單根生長的最大長度lmax,C2={lc+Δl＜llen}判斷當前根段長度是否小于最大根段長度llen.當條件C1及C2同時成立時,單根伸長F(Δl),且更新模式字符T(o,t,l,c,lc)為T(o,t+Δt,l+Δl,c,lc+Δl);當C1成立,C2不成立時,表示根段長度達到分枝長度,因此除進行伸長外并產生新的分枝.我們用符號B(o+1,dc,c+1)表示新的分枝產生節點,dc表示生成新的分枝延遲時間.

單根分枝產生式表述如式(5)所示.

Nmax表示單根最大分枝數目;當單根分枝數目未達到最大值且延遲時間已到即條件c＜Nmax＆d＜=0 成立時,使用SetColor(o)命令設置新生根顏色,并使用Down(ran(90))與RollL(ran(360))命令實現新生根的軸向與徑向偏轉.當單根分枝數目未達到最大值但延遲時間未到即條件c＜Nmax＆d＞0 成立時,將延遲時間減少時間步長.否則,當到單根分枝數目達到最大值時,停止產生分枝.

2.3 水稻根系結構模型

水稻種子根最先產生,我們用模式字符R表示種子根發根結點,則由R形成種子根的過程可用產生式如式(6)描述.使用SetColor(0)命令設置種子根顏色,并將模式字符T所含參數,包括種子根所處的分枝層次o,生長時間t,當前長度l,分枝數目c,前位置距第c個分枝的長度lc初始化為0.

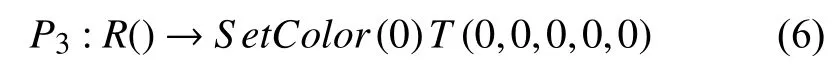
不定根發根節點我們用模式字符N(tc,tt),其中參數tc,tt分別表示根節點距上一次發根的時間及其生存周期.則由發根節點N(tc,tt)生成不定根的產生式定義如式(7)所示.

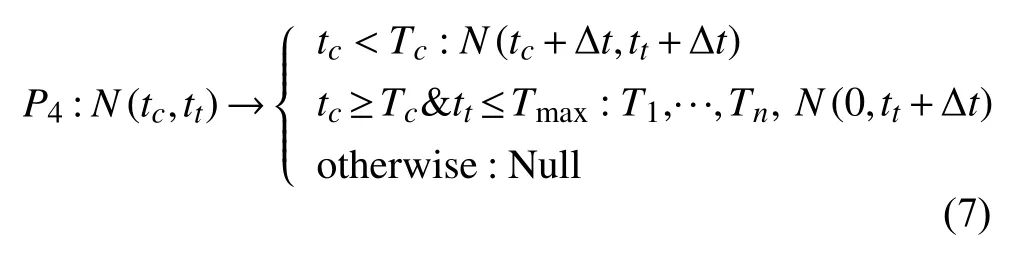
Tc表示水稻莖基發根節點上產生不定根的時間間隔,Tmax表示發根節點產生不定根的最大時間.當未到發根時間間隔時,更新模式字符N(tc,tt)參數為N(tc+Δt,tt+Δt);當到達發根時間間隔且未到最大生根時間時,N(tc,tt)被Ti,i=1,···,n代替,其中Ti=S B()S etColor(0)RollL(ran(360°))Down(ran(90°))T(0,0,0,0,0)EB(),i=1,…,n表示根節點產生新的不定根表達式,同時n為一次產生不定根數目;其中SB()和EB()命令表示產生新的分枝;否則根節點停止產生不定根.P1～P4構成了水稻根系L 文法的產生式集合P.

由此,我們可定義水稻根系L 文法的公理如式(8)所示.

其中,m表示發根節點.通過迭代并不斷應用產生式,模擬水稻根系動態生長過程,由此產生整個水稻根系.

3 水稻根系可視化

3.1 Turtle 坐標系

Turtle 命令包括F、RollL、Down、SB、EB、SetColor等,用于描述水稻根系在三維空間生長過程中單根伸長、分枝、方向等形態變化.在Turtle 幾何學中,Turtle 的狀態是由位置向量及方向向量構成的一個向量組.執行Turtle 命令后,Turtle 由當前狀態轉換到另外一個狀態,新的Turtle 狀態是執行相應的操作后新生成的位置和方向向量組成.Turtle 狀態描述了一個局部坐標系S,而每一個Turtle 命令可表示成一個轉換矩陣T.執行Turtle 命令后,當前坐標系S變換到一個新的坐標系S',如式(9)所示.

在三維Turtle 坐標系中,Turtle 坐標系S是由向前、向左及向上3 個方向向量H、L、U和位置向量P構成,如式(10)所示.

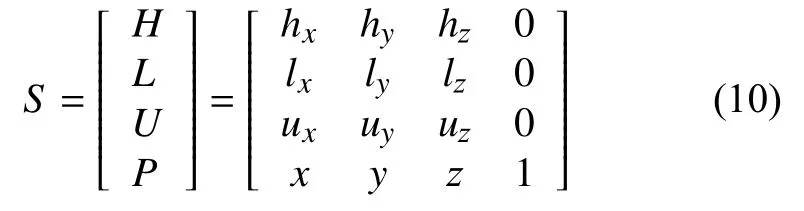
其中,方向向量H、L、U兩兩垂直,并滿足H=L×U.

3.2 Turtle 命令解釋

在Turtle 解釋過程中,每一個Turtle 命令通過式(9)改變當前Turtle 坐標系到下一個狀態.在三維Turtle 幾何坐標系中,每一個Turtle 命令對應一個4×4變換矩陣如表1.

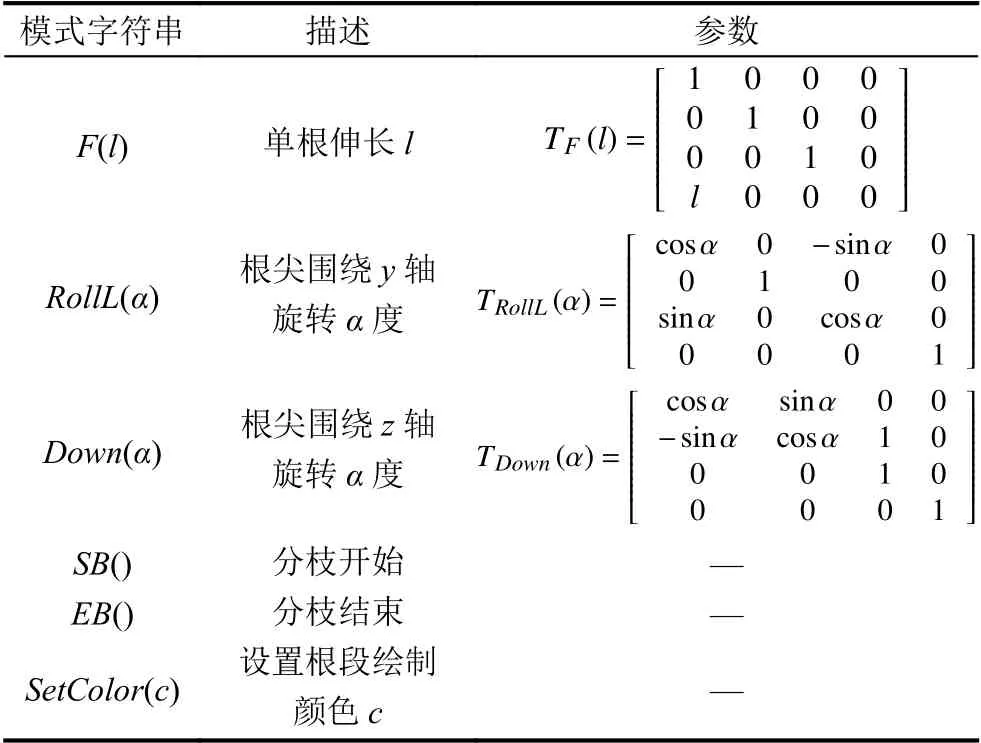
表1 Turtle 命令

Turtle 分支命令SB,EB并不進行任何坐標系變換操作,只將當前Turtle 狀態存入堆棧,或從堆棧取出棧頂數據作為當前Turtle 狀態.它表示具有相同父親的根系子分支具有的Turtle 狀態,即這些子分支在Turtle 坐標系中具有相同的起點.SetColor命令只改變根系顏色,與坐標變換無關.通過上述命令的解釋實現水稻伸長與分枝的圖形繪制,從而實現水稻根系生長過程的可視化.

4 實驗及結果

實驗中我們假定單根最多產生3 次分化,因此每個單根所處的分枝層次分別為0,1,2.根據水稻根系生長特性,單根生長時間間隔定義為Δt=1 (單位:天),也是L 系統中進行模式字符串迭代、Turtle 命令圖形解釋的時間間隔.處于不同層次的單根產生的最大分枝數目定義為Nmax[]={50,10,5},根節點上不定根發根時間間隔定義為Tc=2 (單位:天),根節點產生不定根的最大時間定義為Tmax=150 (單位:天),根節點一次產生不定根最大數目定義為n=2,初始不定根發根節點數定義為m=1.而針對處于不同分枝層次的單根,相關參數定義如表2.

L-Studio 是由Prusinkiewicz 和Hanan 開發,使用L 系統專門對植物生長過程建模的可視化工具.包含cpfg和lpfg[21]兩個模擬器,一個圖形瀏覽器,用于組織和訪問本地和遠程機器上的對象,以及一系列用于創建和修改對象的編輯器和其他建模工具.本文利用Lstudio 工具以及lpfg模擬器對水稻根系生長及分枝規則進行編程實現如圖2所示.

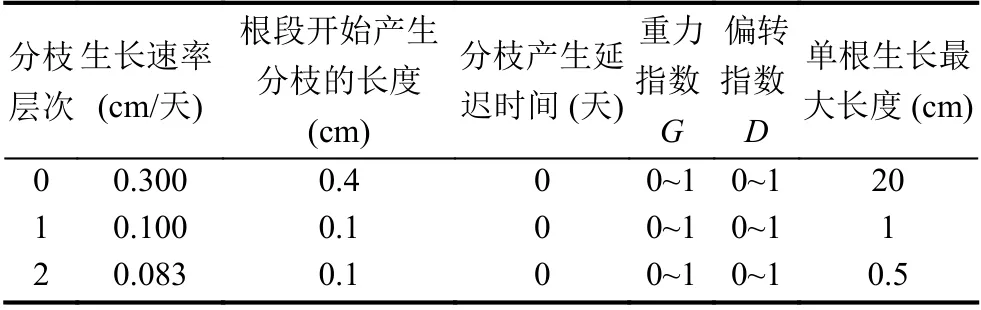
表2 單根建模參數

圖2 水稻根系建模與可視化窗口

當處于不同分枝層次的單根重力指數與偏轉指數相同且定義為G=0.3,D=0.25 時,可得到水稻根系動態生長過程模擬,圖3展示了20,40,60,80 天水稻根系模擬結果.在模擬過程中,種子根最先從種子胚部生長發育,然后越來越的不定根從發莖基部根節點生出.種子根與不定根發生一次分枝,一次分枝再發生二次分枝,直至形成整個龐大的根系.

圖3 當G=0.3,D=0.25 時20,40,60,80 天水稻根系生長模擬

為了研究重力指數G對水稻根系生長的影響,我們定義概率P(x＜α)=(α/180)1-G,其中θ為軸向偏轉角,取值范圍為[-180,180],當重力指數G分別取0,0.3,0.6,0.9 時,P與α之間關系如圖4所示.

當偏轉因子取特定值D=0.25 時,分別模擬G=0,0.3,0.6,0.9 時80 天水稻根系生長情況,結果如圖5所示.不同分枝層次的單根所對應的重力指數G與偏轉指數D取相同值.當G=0時,軸向偏轉角完全隨機生成,不受重力影響.當G值逐漸增大時,水稻根系受重力影響越來越大,向地性也更加明顯.由于根系生長的土壤中,土壤承受了根系的一部分重力,所以向地性不如地上部分明顯.當G值在0.3 附近時,水稻根系生長模擬結果比較符合實際情況.

同樣地,為了研究偏轉指數D對水稻根系生長的影響,我們定義概率P(x＜β)=(β/360)1/D,其中β為徑向偏轉角,取值范圍為[0,360].當偏轉指數D分別取0.0001,0.3,0.6,0.9 時,P與β之間關系如圖6所示.當重力因子取特定值G=0.3 時,分別模擬D=0.0001,0.3,0.6,0.9 時80 天水稻根系生長情況,結果如圖7.不同分枝層次的根系所對應的重力指數G與偏轉指數D取相同值.當偏轉指數D接近0 時,水稻根系近乎直線生長.當偏轉指數D值越來越大時,單根生長方向的偏轉也越來越大.對比實際情況,當D值在0.3 附近,水稻根系生長模擬結果比較符合實際情況.

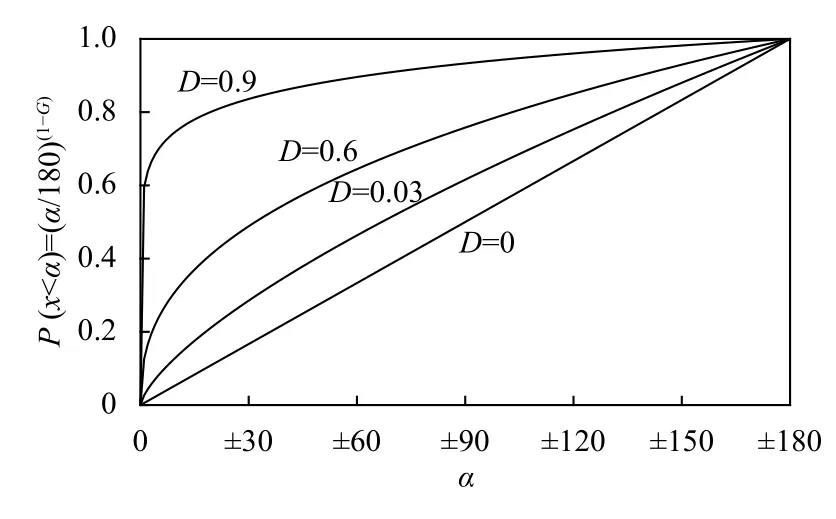
圖4 P(x＜α)=(α/180)1-G曲線

圖5 當G=0,0.3,0.6,0.9,D=0.25 時,80 天水稻根系生長模擬

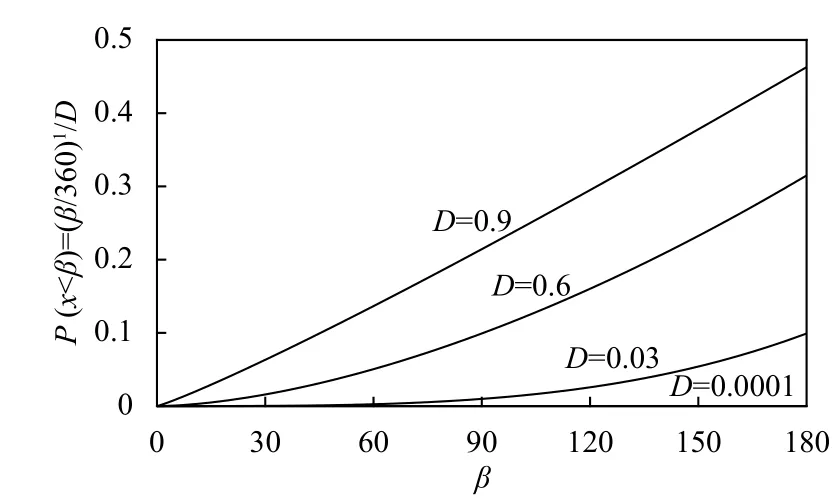
圖6 P(x＜β)=(β/360)1/D曲線

5 結論與展望

水稻根系生長過程建模與可視化是虛擬水稻模型研究的重要組成部分.在分析水稻根系空間分布特性,水稻根系發育進程的形態結構、生長及分布特點和規律的基礎上,本文利用L 系統定義了水稻單根生長規則,單根分枝產生規則等,構建了水稻根系結構模型,模擬水稻根系在重力因子及偏轉因子影響下,根系動態生長變化過程,并利用L-studio 實現水稻根系生長過程的三維可視化.研究表明:(1)當重力因子G=0 時,軸向偏轉角完全隨機生成,不受重力影響.當重力因子G值逐漸增大時,水稻根系受重力影響越來越大,向地性也更加明顯.(2)當偏轉指數D≈0 時,水稻根系幾乎沒有偏轉,根系呈直線生長.當偏轉指數D值越來越大時,單根生長方向的偏轉也越來越大.(3)對比實際情況,當G與D值在0.3 附近取值時,水稻根系生長模擬結果比較符合實際情況.在后續的研究工作中,將會引入土壤環境模型,對環境影響下水稻根系生長過程進行建模,使得仿真結果更加貼近實際.

圖7 當D=0.001,0.3,0.6,0.9 時,80 天水稻根系生長模擬