空間變導流能力壓裂井CO2 驅試井分析

崔永正，姜瑞忠，郜益華，喬 欣，王 瓊

（1.中國石油大學（華東）石油工程學院，山東青島 266580；2.中海油研究總院有限責任公司，北京 100028；3.中國石油北京油氣調控中心，北京 100007）

0 引言

在我國，低滲透油藏具有分布廣，儲量大，開發潛力大等特征［1-2］，低滲透油田的高效開發利用對確保我國油氣可持續發展具有重要戰略意義。針對低滲透油田滲透率低，水驅開發效果差的特點，壓裂井與CO2驅結合的開發方式引起了國內外學者的關注［3-4］。

試井作為了解地下油藏和流體性質的重要手段，國內外許多學者針對CO2驅試井解釋數學模型進行了大量的研究。Tang 等［5］建立了基本的三區復合油藏模型；Su 等［6］、閻燕等［7］、李友全等［8］、蘇玉亮等［9］研究了考慮應力敏感的CO2驅直井的三區復合模型，并對各因素進行了敏感性分析；Li 等［10-11］開展了基于組分模型的CO2驅直井及多段井試井研究，對試井曲線及各組分在地層中的分布情況進行了分析；姜瑞忠等［12］建立了基于水平井的CO2驅三區復合試井模型，將典型曲線分為9 個階段，并對各因素進行了敏感性分析。

壓裂井試井作為近年來研究的熱點，Teng 等［13］、Guo 等［14］、姬靖皓等［15］、Jia 等［16］針對壓裂井試井模型進行的大量研究都是以恒定裂縫寬度作為假設，但實際上支撐裂縫寬度從縫端到縫口逐漸變化，恒定縫寬模型假設與實際不符。針對變導流能力裂縫，國內外學者進行了相關研究，郭建春等［17］建立了基于楔形縫的壓裂直井產量預測模型，表明楔形縫產量預測模型能夠以更真實的裂縫形態來預測壓后產量；孫賀東等［18］利用混合有限元方法對變導流能力多級壓裂水平井現代產量遞減進行了分析，發現裂縫變導流能力主要對產量遞減曲線產期產生影響；高陽等［19］建立了考慮變導流能力的多級壓裂水平井試井模型，并提出了變導流能力裂縫的處理方法；Luo 等［20］建立了變導流能力壓裂直井的試井分析模型；Huang 等［21］建立了考慮裂縫部分閉合的壓裂直井試井模型；Liu 等［22］建立了考慮復雜裂縫形態及變導流能力的試井模型；Liu 等［23］建立了三層油藏考慮變導流能力壓裂直井的解析解，并進行了求解和敏感性分析。綜上所述，目前尚沒有考慮裂縫空間變導流能力的CO2驅試井模型。

因此，在前人研究的基礎上，建立低滲透油藏空間變導流垂直裂縫井CO2驅試井解釋模型，利用Laplace 變換等數學方法獲得拉氏空間解析解，利用Stehfest 數值反演繪制典型特征曲線并進行影響因素分析。

1 模型的建立與求解

1.1 物理模型

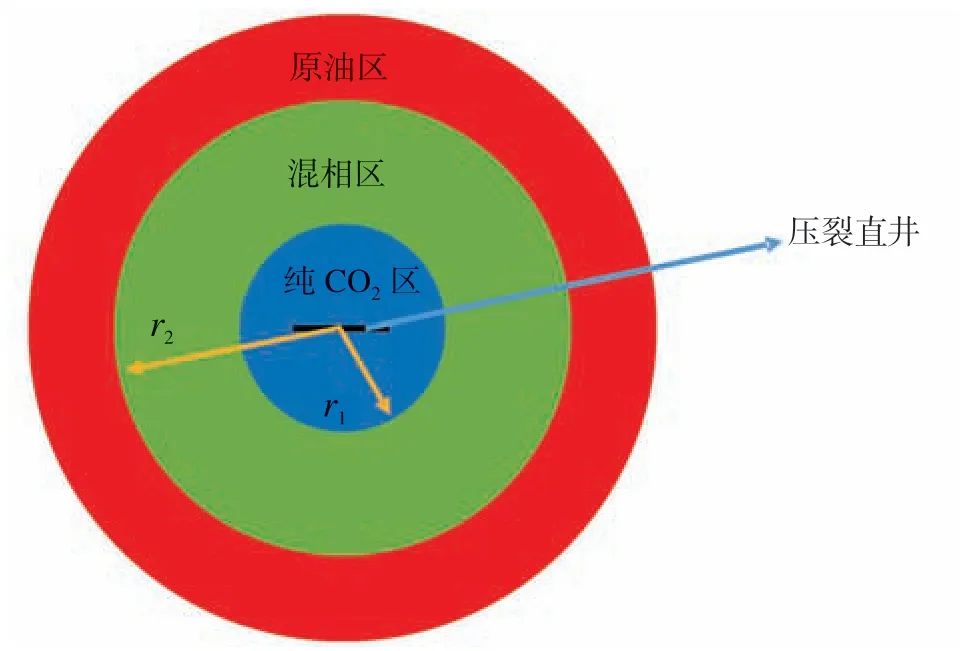
圖1 CO2 驅油三區復合物理模型Fig.1 Physical modeling of three-zone composite vertical fractured wells for CO2 flooding

根據CO2驅油過程中油藏流體的不同性質，基于三區復合模型滲流理論，物理模型如圖1 所示。內區充滿CO2，表現為CO2氣相單相滲流，半徑為r1；過渡區為在混溶/不混溶條件下CO2與原油的混合區，半徑為r2；外區為單相儲層原油區。該復合模型的假設條件包括：①油氣藏中油氣共存；②流體滲流過程中溫度恒定，且遵循達西滲流原理；③儲層為水平、均質、等厚和無限大，初始壓力處處相等；④裂縫半長為XF，裂縫的寬度不等，為空間變導流能力；⑤忽略重力與毛管壓力的影響；

1.2 數學模型

1.2.1 儲層滲流數學模型

根據上述三區復合模型的假設，對各區質量守恒方程和綜合方程進行推導。

（1）內區

內區為純CO2區，為氣相單相滲流，其質量守恒方程為

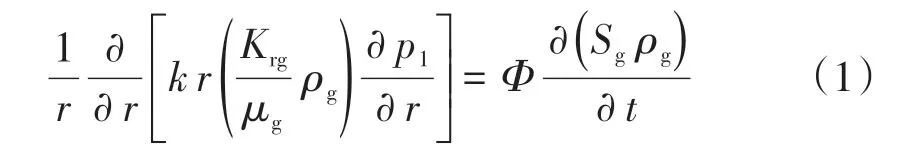
式中：r為油藏半徑，m；k油藏滲透率，mD；Krg為氣相相對滲透率；μg為氣相有效黏度，Pa·s；ρg為氣相密度，kg/m3；Sg為氣相的飽和度；Φ為孔隙度；p1為CO2區地層壓力，Pa。

式（1）可進一步化簡為

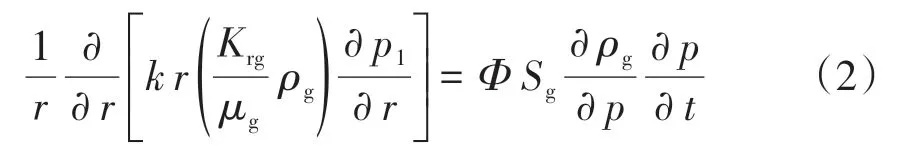
其中：

式中：Cg為氣體壓縮系數，1/Pa；Vg為氣相體積，m3。

式（2）可進一步化簡為

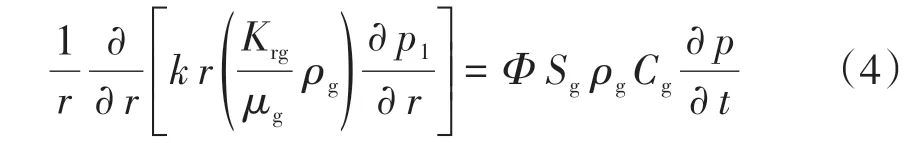
上述方程為非線性方程，引入擬壓力對上述方程進行線性化

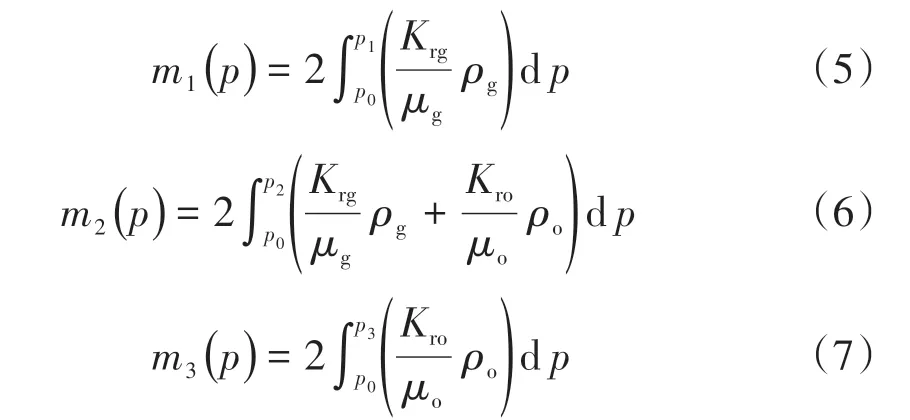
式中：p0為參考壓力，Pa；p2為過渡區地層壓力，Pa；p3為原油區地層壓力，Pa。

引入式（2），對上式進行線性化，得

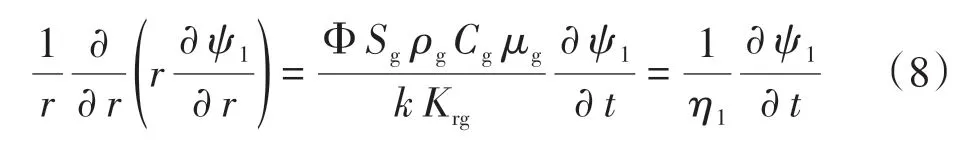
利用表1 中無因次量，對上述數學模型進行無因次化，并進行Laplace 變換，內區綜合方程為

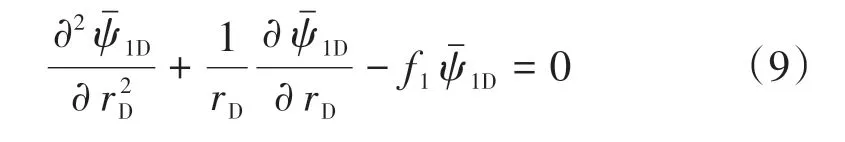
式中：f1=u；u為Laplace 變量。

（2）中間區

中間區為CO2與原油的混合區，其質量守恒方程為

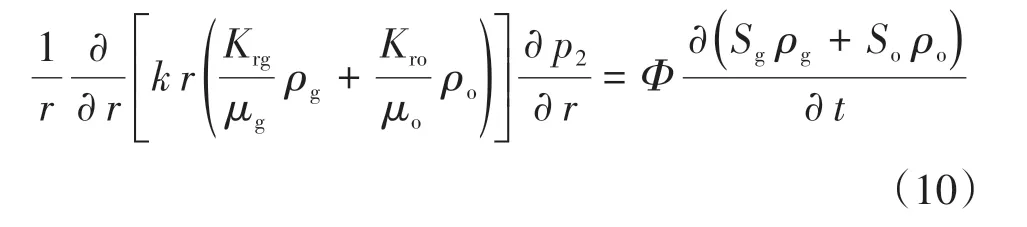
式中：Kro為油相相對滲透率；μo為油相有效黏度，Pa·s；ρo為油相密度，kg/m3；So為氣相的飽和度。

利用式（6）中擬壓力對上式（10）進行線性化，利用表1 無因次量，對上述數學模型進行無因次化，進行Laplace 變換，中間區綜合方程為：

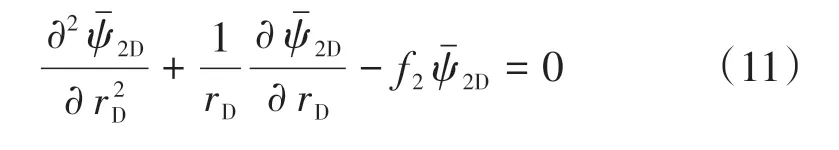
式中：f2=ω12uo。

（3）外區

外區為單相原油區，原油單相流動，其質量守恒方程為

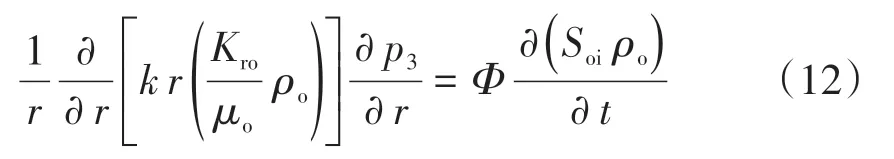
式中：Soi為原始含油飽和度。

利用式（7）對式（12）進行線性化，利用表1無因次量，對上述數學模型進行無因次化，進行Laplace變換，外區綜合方程為

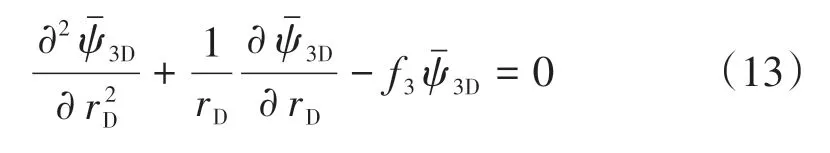
式中：f3=ω13u。

（4）邊界條件

外邊界條件為

線源內邊界條件為

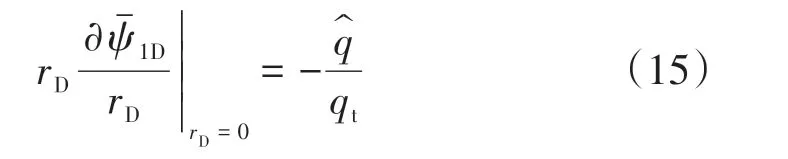
一區與二區交界面條件

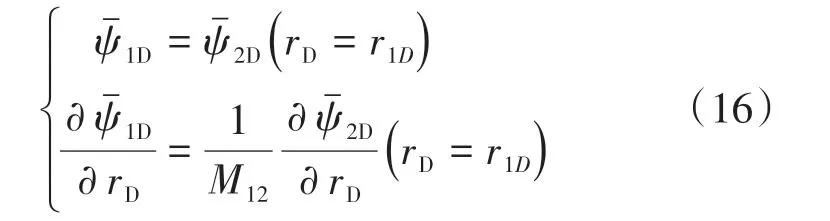
二區與三區交界面條件

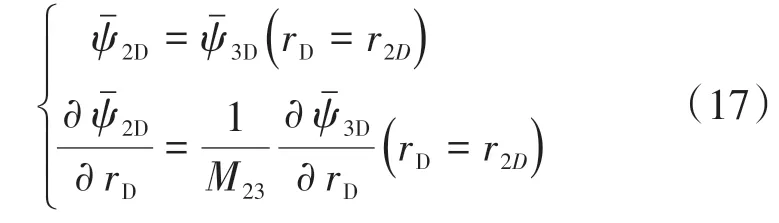
對式（9）、式（11）、式（13）及邊界條件進行聯立求解，可以得到CO2驅內區線源所引起的壓力響應為

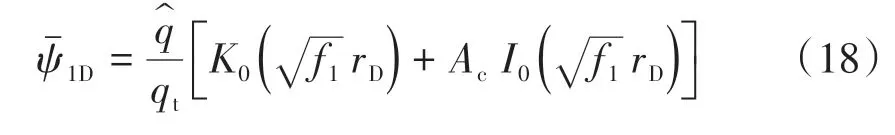
表1 無因次量Table 1 Definitions of the dimensionless variables

1.2.2 有限導流能力壓裂直井方程

水力裂縫孔隙體積很小，忽略孔隙體積變化的影響，裂縫滲流滿足達西定律，可得壓裂裂縫中質量守恒方程為：

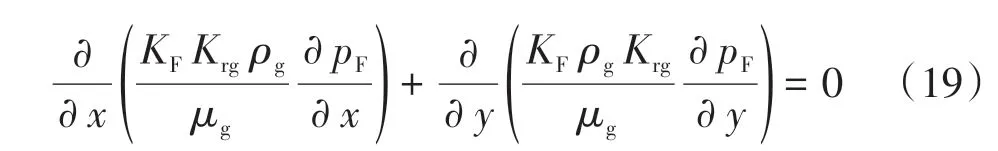
式中：KF為水力裂縫滲透率，mD；pF為水力裂縫壓力，Pa。

由于水力壓裂形成的裂縫寬度解一般較小，故在式對等式左端第2 項取積分平均處理，從而可得到

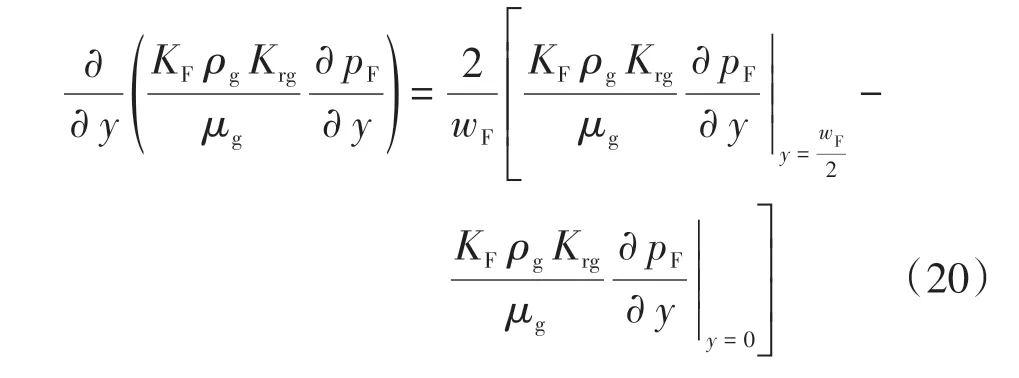
式中：wF為裂縫寬度，m。

單位裂縫長度流量可表示為

式中：h為地層厚度，m；qL為水力裂縫單位長度流量，kg/（m·s-1）。

從水力裂縫右翼流入井筒的產量為

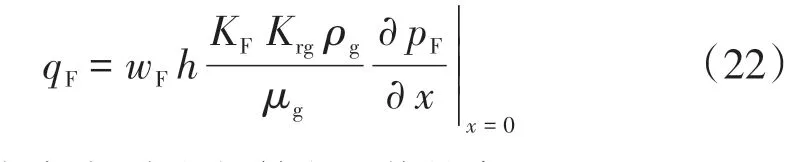
式中：qF為水力裂縫右翼流入井的產量，kg/s。

對式（20）、式（21）、式（22）進行線性化，利用表1 無因次量進行無因次化，并進行Laplace 變換，可得壓裂直井綜合方程。其中有限導流裂縫內流動方程：

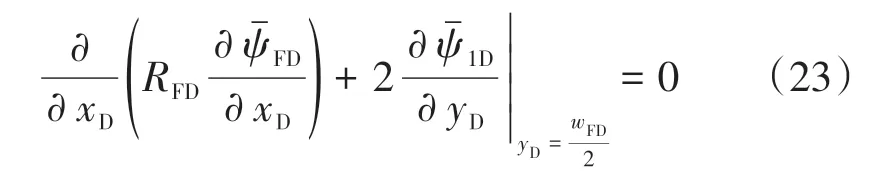
定產內邊條件

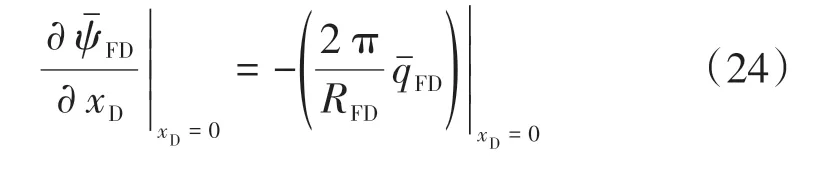
裂縫與儲層交界面條件

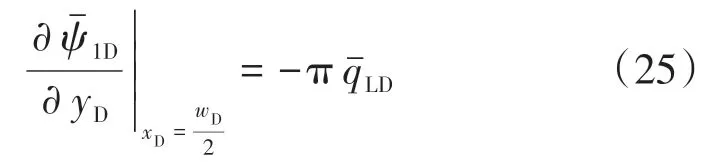
裂縫根段封閉條件

1.3 數學模型求解

對于壓裂井而言，人工裂縫是油氣的主要流動通道，裂縫的物理模型對計算結果有重要影響。在裂縫閉合后，裂縫寬度不是恒定的，靠近裂縫端部的鋪砂濃度較小，靠近井眼部分的裂縫鋪砂濃度較高，最終形成的支撐裂縫寬度從縫端到縫口逐漸變寬，如圖2 所示，裂縫導流能力隨裂縫長度而減小，假設計算公式［18］為

式中：RFD0為縫口處裂縫無因次導流能力，m3；bs空間變導流能力系數；xF為水力裂縫半長，m。

利用高陽等［19］提出的方法對變導流能力裂縫進行處理，將無因次水力裂縫半長等分成n份，步長ΔxD，Dj為第j個裂縫單元格的中點，xDj為第j個離散端點，如下圖2 所示，當離散單元無限小時，假設每個離散單元內流量均勻分布。

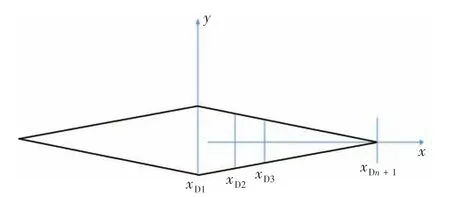
圖2 水力裂縫劃分示意圖Fig.2 Schematic of discretization of the hydraulic fracture

從水力裂縫示意圖中，可得裂縫離散單元端點和中點表達式為

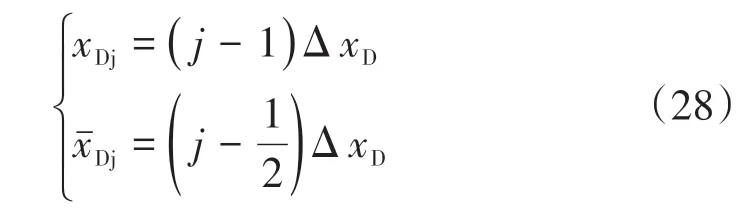
將式（25）帶入式（23）中，可得

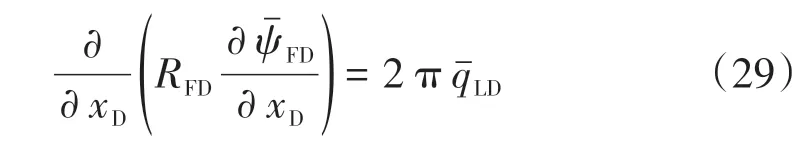
對兩側同時進行積分，得：

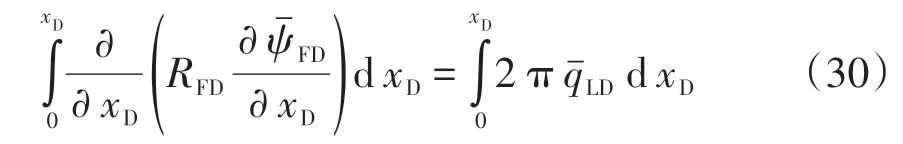
將邊界條件式（24）帶入式（30），化簡可得

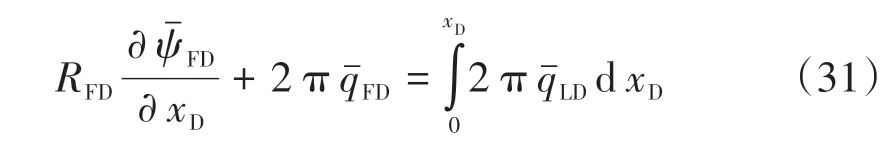
對式（31）兩側同時進行積分，得

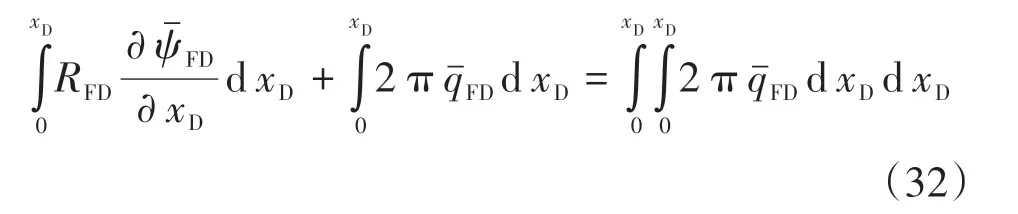
式（32）可進一步化簡為

水力裂縫半長等分成n份，則第i段裂縫的壓力降為

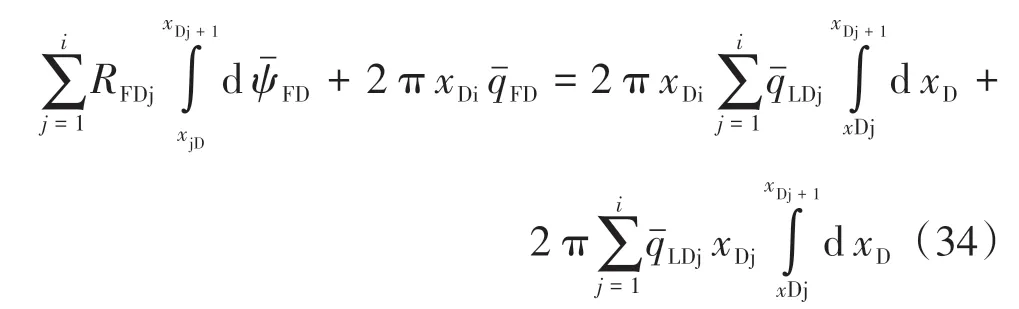
式（34）可進一步化簡為

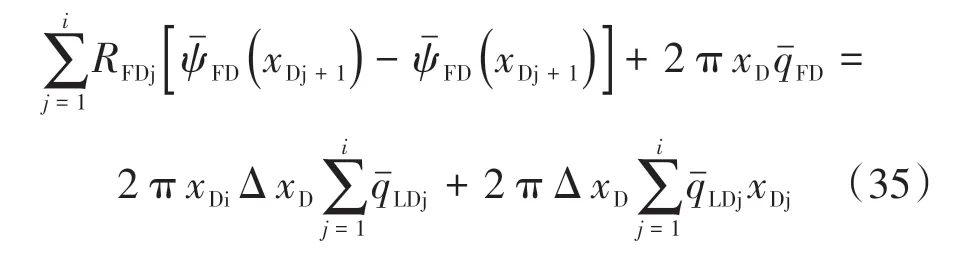
當i=1 時，對式（34）進行化簡，可得

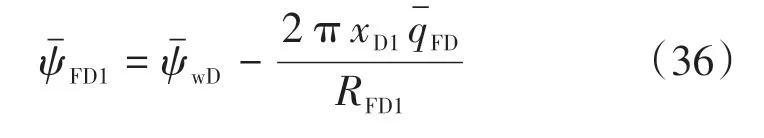
當i=2 時，對式（34）進行化簡，可得

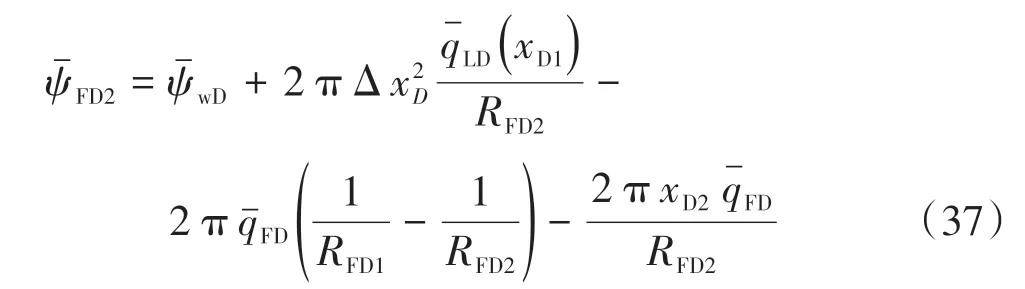
當i=3 時，對式（34）進行化簡，可得

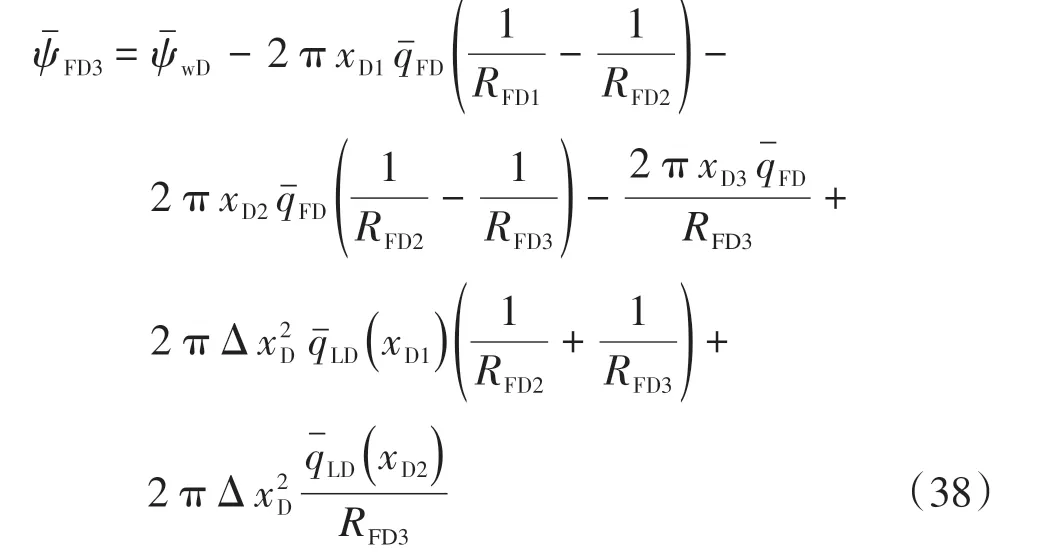
則第i段裂縫的壓力解為

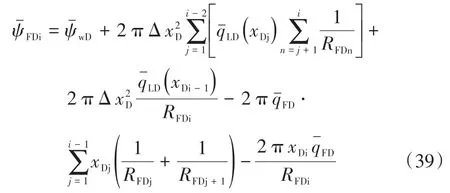
由式（18）可得，第i段裂縫所產生的壓力相應為

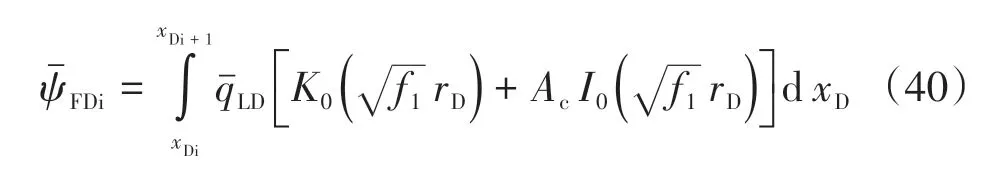
裂縫內流體總量等于各裂縫段流量之和

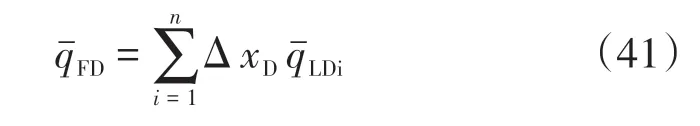
聯合式（39）、式（40）、式（41），可得到n+1 個線性方程，對應n+1 個未知數。對方程組進行求解，利用杜哈美原理考慮井筒儲集效應和表皮因子的影響，得到如下無因次井底壓力

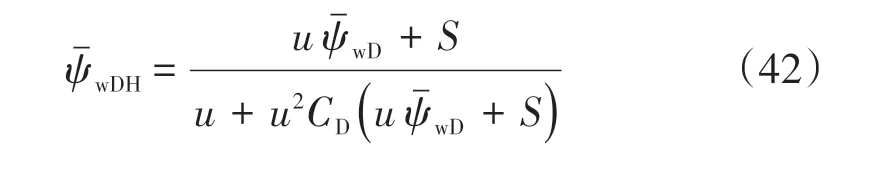
2 特征曲線分析

根據上述模型推導，編制程序計算壓力及壓力導數曲線，繪制有限導流能力裂縫CO2驅三區復合油藏典型試井曲線。相關參數及具體流態劃分如圖3 所示，其典型試井曲線可分為以下9 個階段：①井筒儲集階段，壓力及壓力導數曲線斜率均為1；②井筒儲集后過渡階段；③雙線性流階段，此時地層及水力裂縫都存在線性流，擬壓力曲線及擬壓力導數曲線為斜率為“1/4”的平行直線；④地層線性流階段，擬壓力曲線及擬壓力導數曲線為斜率為“1/2”的平行直線；⑤第一徑向流，此時內區以徑向流形式向壓裂裂縫及井內流動；⑥第一過渡流，此時中間區向內區流動，由于中間區流度小于內區流度，試井曲線出現抬升；⑦第二徑向流，流體在中間區徑向流動，壓力導數曲線為一條水平線，其數值為0.5M12；⑧第二過渡流，最外區向中間區流動，由于最外區流度小于中間區流度，試井曲線出現抬升；⑨第三徑向流，流體在最外區徑向流動，壓力導數曲線為一條水平線，其數值為0.5M12*M23。

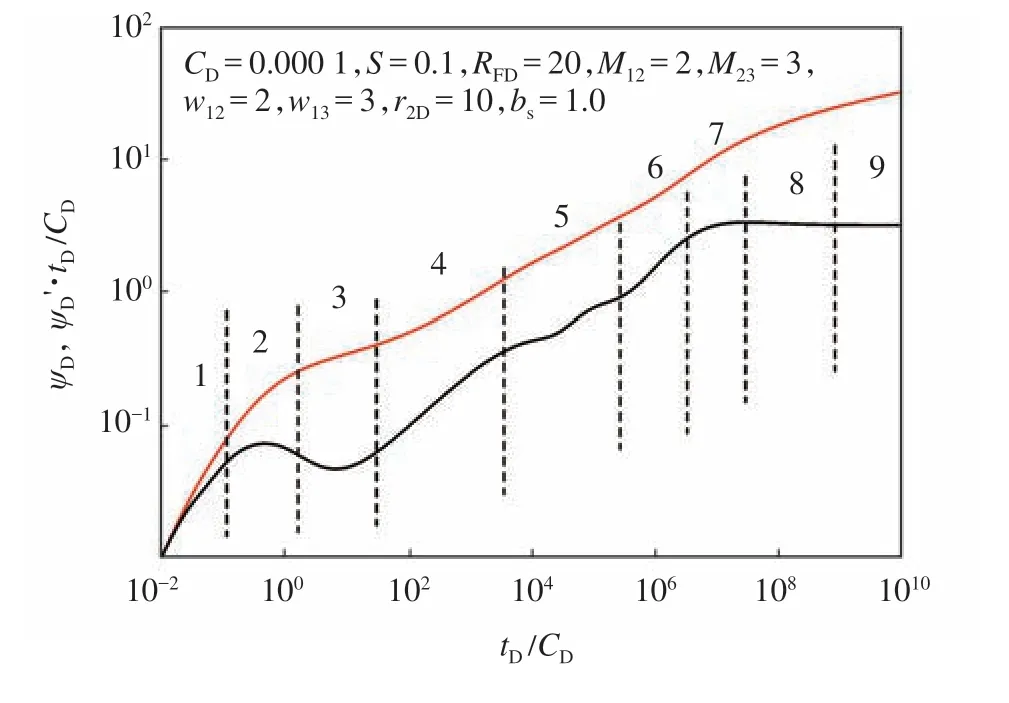
圖3 試井典型曲線Fig.3 Type curve of pressure transient

3 參數敏感性分析

3.1 裂縫導流能力的影響

裂縫導流能力作為水力裂縫的重要指標，由水力裂縫的滲透率及水力裂縫寬度決定，水力壓裂過程中的壓裂液及支撐劑都會對其造成巨大影響。從圖4 可以看出，裂縫導流能力主要對雙線性流及線性流階段產生影響，裂縫導流能力越大，壓力及壓力導數越小，雙線性流階段越不明顯，導流能力達到一定程度，雙線性流消失，試井曲線變為無限導流能力試井曲線。裂縫導流能力越強，CO2越容易注入，能夠更好地對低滲透油藏進行開發。

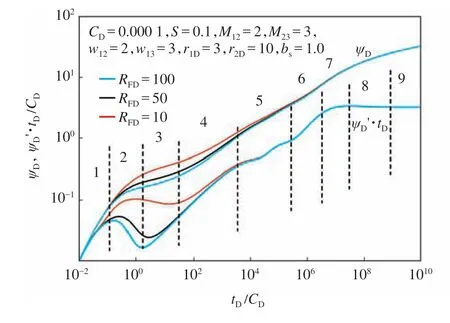
圖4 裂縫導流能力對試井曲線的影響Fig.4 Effect of fracture conductivity on pressure transient type curve

3.2 空間變導流的影響

裂縫導流能力受施工影響，裂縫一般為楔形縫，裂縫導流能力隨裂縫的延伸而減小。本文設置空間變導流能力系數bs為0，0.8，1.0 等3 組數據，裂縫空間導流能力分布如圖5 所示。考慮裂縫導流能力變化后，從如圖6 可以看出，早期壓差增大，壓力及壓力導數曲線都都呈現一定的上升，表現出表皮系數增大的現象。不考慮裂縫導流能力的空間變化會對試井解釋造成較大影響。

圖5 無因次導流能力分布曲線Fig.5 Schematic of space variable conductivity of the hydraulic fracture

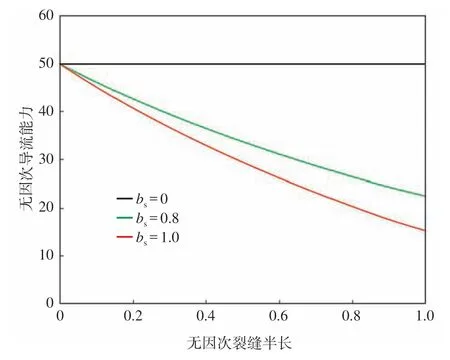
圖6 空間變導流系數對試井曲線的影響Fig.6 Effect of space variable conductivity on pressure transient type curve

3.3 一區半徑的影響

隨著注入CO2的不斷增加，CO2區半徑會不斷增大。設置不同的CO2區無因次半徑，試井曲線如圖7 所示，內區半徑主要對內區徑向流和過渡段產生影響，內區半徑越小，過渡流出現的時間越早，內區徑向流持續時間越短，內區半徑過小時，內區徑向流將會被掩蓋。

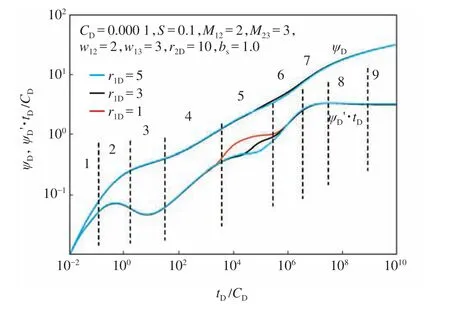
圖7 CO2 區半徑對試井曲線的影響Fig.7 Effect of r1D on rate transient type curve

3.4 二區半徑的影響

CO2注入量、擴散系數及原油的物性特征都會對過渡區的半徑產生較大影響。設置不同的過渡區無因次半徑，試井曲線如圖8 所示，過渡區半徑主要對第二徑向流和過渡段階段產生影響，過渡區半徑越小，第二過渡流出現的時間越早，第二徑向流持續時間越短，過渡區半徑過小時，第二徑向流將會被掩蓋。

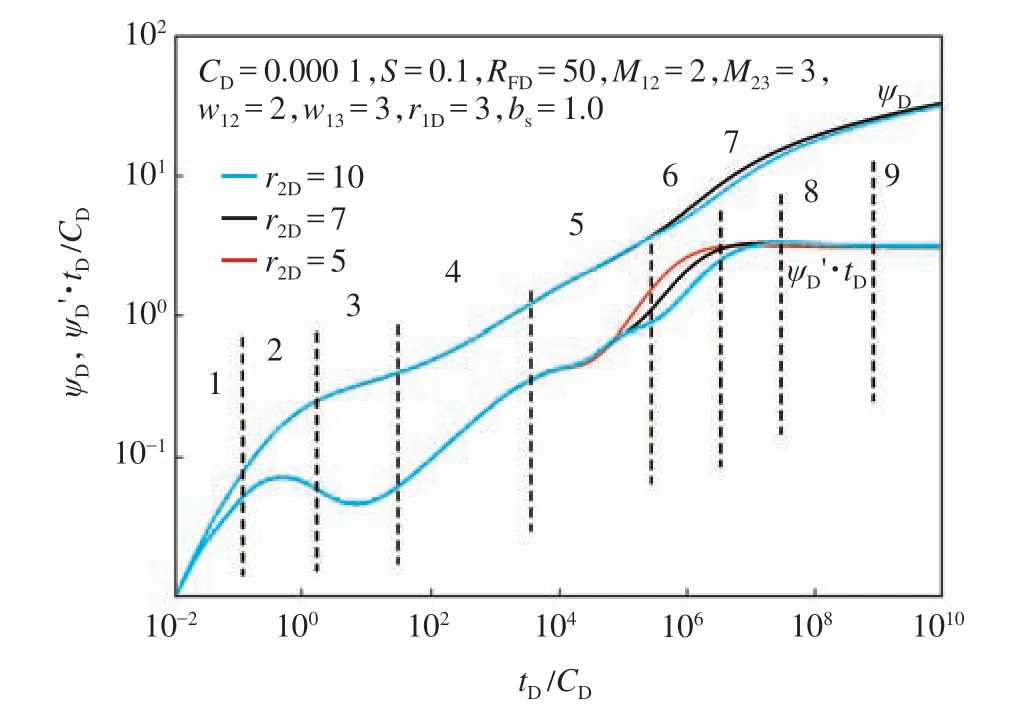
圖8 過渡區半徑對試井曲線的影響Fig.8 Effect of r2D on rate transient type curve

3.5 CO2 與過渡區流度比M12 的影響

流度是影響流動和壓力波傳播的重要因素，過渡區為油氣混合區，其流度小于內區純氣相流度。設置不同的內區與過渡區流度比，試井曲線如圖9所示，從圖中可以看出，內區與過渡區流度比主要對過渡區及最外區流動階段產生影響，內區與過渡區流度比越大，則表示過渡區流度越小，其流動阻力較大，則過渡區及最外區流動階段所消耗的壓差越大，因此過渡區及最外區流動階段壓力及壓力導數曲線都會抬升。

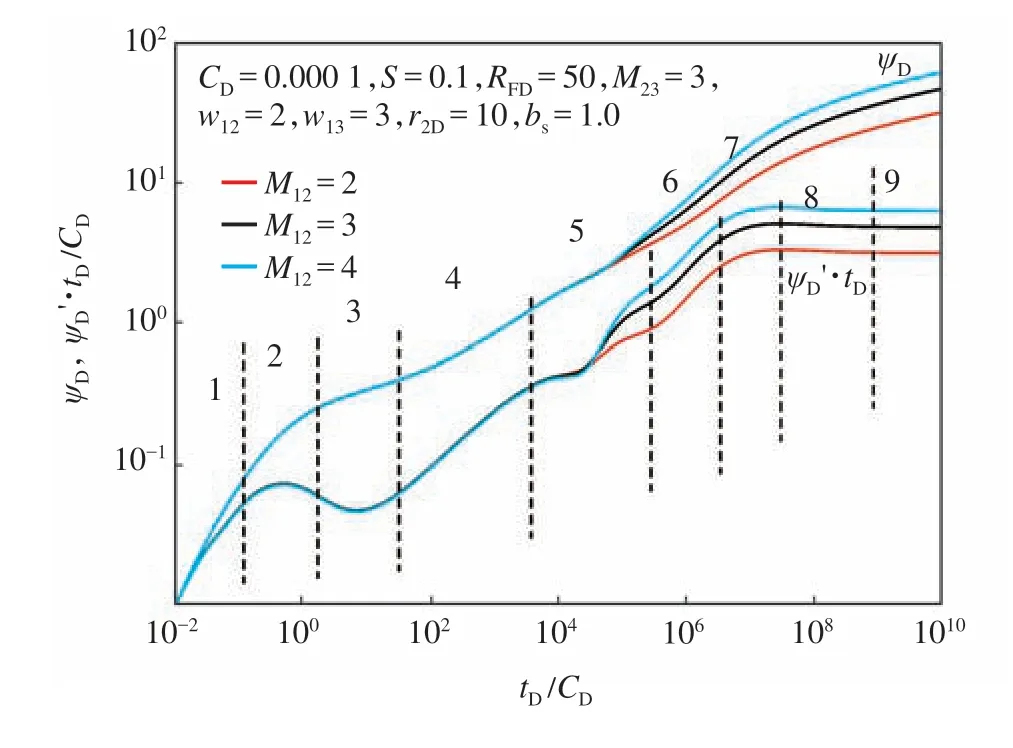
圖9 過渡區與原油區流度比對試井曲線的影響Fig.9 Effect of mobility ratio M23 on rate transient type curve

3.6 過渡區與原油區流度比M23 的影響

過渡區為油氣混合區，最外區為純油相流動，最外區流度小于過渡區流度。設置不同的過渡區與最外區流度比，試井曲線如圖10 所示，過渡區與最外區流度比主要對最外區流動階段產生影響，過渡區與最外區流度比越大，則表示對應的最外區流動越小，最外區流動阻力越大，最外區流動階段所消耗的壓差越大，因此最外區流動階段壓力及壓力導數曲線都會抬升。

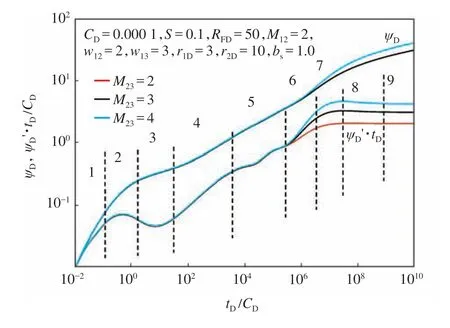
圖10 CO2 與過渡區流度比對試井曲線的影響Fig.10 Effect of mobility ratio M12 on rate transient type curve

4 結論

（1）利用Laplace 變換對CO2三區復合空間變導流能力壓裂直井解析解進行了推導，利用Stehfest數值反演繪制試井典型曲線。典型曲線可分為井筒儲集段、井筒儲集后過渡段、雙線性流段、地層線性流段、第一徑向流段、第一過渡流段、第二徑向流段、第二過渡流段、第三徑向流段共9 個階段。

（2）裂縫導流能力越大，雙線性流階段壓力及壓力導數越小，雙線性流階段越不明顯，導流能力達到一定程度，雙線性流消失，試井曲線變為無限導流能力試井曲線。裂縫導流能力受施工影響，裂縫一般為楔形縫，考慮裂縫導流能力變化后，早期壓差增大，壓力及壓力導數曲線都呈現一定的上升，表現出表皮系數增大的現象。

（3）CO2半徑越小，第一過渡流階段出現的時間越早，內區徑向流持續時間越短；過渡區半徑越小，第一過渡流階段出現的時間越早，第二徑向流持續的時間越短。

（4）內區與過渡區流度比越大，則過渡區及最外區流動階段所消耗的壓差越大，因此過渡區及最外區流動階段壓力及壓力導數曲線都會抬升；過渡區與最外區流度比越大最外區流動階段所消耗的壓差越大，最外區流動階段壓力及壓力導數曲線都會抬升。